素混凝土桩复合地基高层建筑沉降研究

王超楠，胡晓鹏，刘明振

(1.西安建筑科技大学 建筑设计研究院， 陕西 西安 710055；2.西安建筑科技大学 土木工程学院， 陕西 西安 710055)



素混凝土桩复合地基高层建筑沉降研究

王超楠1，胡晓鹏2，刘明振2

(1.西安建筑科技大学 建筑设计研究院， 陕西 西安 710055；2.西安建筑科技大学 土木工程学院， 陕西 西安 710055)

为分析复合地基沉降计算方法在西安地区的适用性，实测了西安地区某住宅小区多个应用素混凝土桩复合地基的高层建筑沉降数据，并将实测数据与多种复合地基沉降计算方法得到的计算结果进行了对比分析，探讨了同类工程地质条件下不同沉降计算方法的适用性，提出了不同计算方法的沉降经验系数。研究表明：在西安地区类似的复合地基沉降计算时，文中第二种统一算法简单易行且其计算结果与实测沉降变形最为接近；压力扩散法所得到的计算结果偏于安全且变异性较小，适于对计算结果进行复核。

高层建筑；复合地基；沉降计算；实测沉降

桩基础和复合地基是目前最常用的高层建筑地基基础形式，而复合地基由于其工程造价较低、工艺简单、施工速度快等优点受到建设单位及设计单位的青睐。其中，素混凝土桩复合地基作为刚性桩复合地基形式之一，与一般柔性桩相比承载力更高。高层建筑的地基基础不但须满足地基承载力的要求，其沉降变形也须符合相关规范的要求，沉降变形的控制一直都是结构设计的重点，关于复合地基沉降的计算方法国内外开展了理论和试验研究，提出了相应的沉降变形计算方法[1-11]。目前，复合地基沉降计算方法主要有两种：《复合地基技术规范》[12](GB/T50783-2012)给出的分段变形叠加法和各种设计软件中基于《建筑地基基础设计规范》[13](GB5007-2011)的分层总和法，这两种计算方法实用性强，但计算中经验系数的取值对计算结果影响极大，不同地区应用中经验系数的取值有较大差异。当复合地基桩在桩长范围内没有坚实的持力层时，即使地基承载力能够满足设计要求，高层建筑的计算沉降量也难以保证。出于对建筑物沉降控制的担忧，设计人员常限制此类复合地基在高层建筑尤其是25层以上的高层建筑中使用。在西安地区，对采用复合地基25层以上的高层建筑沉降量缺乏相对准确的计算和工程经验积累，采用素混凝土桩复合地基的工程案例较少。

本文通过实测西安地区某住宅小区多个应用素混凝土桩复合地基的高层建筑沉降，对比分析实测数据与多种复合地基沉降计算方法得到的计算结果，研究同类工程地质条件下不同沉降计算方法的适用性，提出不同计算方法的沉降经验系数。

1　复合地基沉降计算方法

1.1地基变形分段算法

复合地基的沉降变形可以分为两大部分分别计算：

S=S1+S2

(1)

式中：S1为复合地基加固区复合土层压缩变形；S2为复合地基下卧区压缩变形。

1.1.1S1的计算方法

对于复合地基加固区复合土层压缩变形S1，规范[13]根据复合地基类型给出了不同的计算方法。

(1) 柔性桩复合地基

(2)

式中：Δpi为第i层土的平均附加应力增量；li为第i层土的厚度；ψs1为复合地基加固区复合土层压缩变形量计算经验系数；Espi为第i层复合土体的压缩模量，可利用下式求得。

Espi=mEpi+(1-m)Esi

(3)

式中：m为复合地基置换率；Epi为第i层桩体压缩模量；Esi为第i层桩间土压缩模量。

对于复合土体的压缩模量，《建筑地基处理技术规范》[14](JGJ79-2012)给出了另一种算法。

Espi=fspk/fak·Esi

(4)

式中：fspk为深度修正后的复合地基承载力特征值；fak为基础底面下天然地基承载力特征值。

以上计算方法均将桩体和土体视为复合土体，采用复合压缩模量Esp来计算复合土体的变形，其取值对计算结果有重大影响。其中，式(3)可以通过弹性理论证明但计算结果偏安全[15]，式(4)为经工程验证的工程常用经验算法，在很多工程条件下计算结果均较符合实际沉降结果。

(2) 刚性桩复合地基

(5)

式中：Q为刚性桩桩顶附加荷载；l为刚性桩桩长；Ep为桩体压缩模量；Ap为单桩截面积；ψp为刚性桩桩体压缩经验系数。

此计算方法也属于经工程验证的工程常用经验算法，多用于复合地基置换率较大的刚性桩复合地基。其中桩顶附加荷载的确定与桩土应力比关系很大。对于素混凝土桩之类的刚性桩复合地基，由于桩体刚度较之地基土层相对很大，工程实践中往往将所有基底荷载由桩体承担，桩体压缩模量取素混凝土的压缩模量，桩体压缩经验系数通常取1.0。

1.1.2S2的计算方法

对于S2的计算目前设计中主要采用分层总和法计算：

(6)

式中：ψs2为复合地基加固区下卧土层压缩变形量计算经验系数。对于作用在复合地基加固区下卧层顶部的附加压力pz，根据复合地基类型有以下两种算法。

(1) 压力扩散法—散体材料复合地基

(7)

式中：L为矩形基础底边的长度；B为矩形基础或条形基础底边的宽度；h为复合地基加固区的深度；a0、b0分别为基础长度、宽度方向桩的外包尺寸；p0为复合地基加固区顶部的附加压力；为压力扩散角；f为复合地基加固区桩侧摩阻力。

此种方法中应力扩散角的确定最为关键，各类文献中对应力扩散角的选取也有很多不同的意见，设计中通常以规范[13]中表5.2.7作为应力扩散角确定的主要依据。

(2) 等效实体法—刚性桩复合地基

(8)

此种算法多用于复合地基置换率较大的刚性桩复合地基，其中实体基础侧摩阻力f的取值通常采用工程勘察报告中给出的桩体侧摩阻力标准值。

1.2地基变形统一算法

复合地基的沉降变形S可通过复合地基复合压缩模量Esp及工程勘察报告中给出各层土体的压缩模量Es，采用分层总和法计算得到[14]。

(9)

相比于分层总和法，沉降变形统一算法由于确定参数方便被广泛应用于计算机程序，目前常用的计算软件如PKPM系列均支持此种算法。

2　计算结果与实测数据的对比分析

2.1工程概况

西安地区某住宅小区总建筑面积约40万m2，项目主要由17栋地上28层或33层、地下1层的高层建筑组成，建筑结构均为点板结合品字形布置的剪力墙结构，图1给出了某栋28层建筑物的基础平面布置图。小区范围内土层分布均匀，基底以下影响深度范围内土层自上向下依次为Q3黄土、Q3古土壤、Q3粉质黏土、Q2粉质黏土(局部含薄粗砂夹层)、Q2粉质黏土，具有代表性的各层土体的厚度分布及沉降计算关键工程指标见图2。图中，压缩模量为土体相应工况下应力范围内数值，侧摩阻力标准值为湿陷性预处理后的试验值。

图1建筑地基平面布置图

工程中先使用4 m～7 m不等的素土挤密桩消除场地湿陷性后，采用素混凝土桩复合地基作为复合地基方案。素混凝土桩桩径均为400 mm，桩间距1.4 m，复合地基面积置换率为0.1，桩身混凝土强度为C25，桩长22 m。复合地基计算复合地基承载力715 kPa，设计采用承载力特征值为630 kPa。

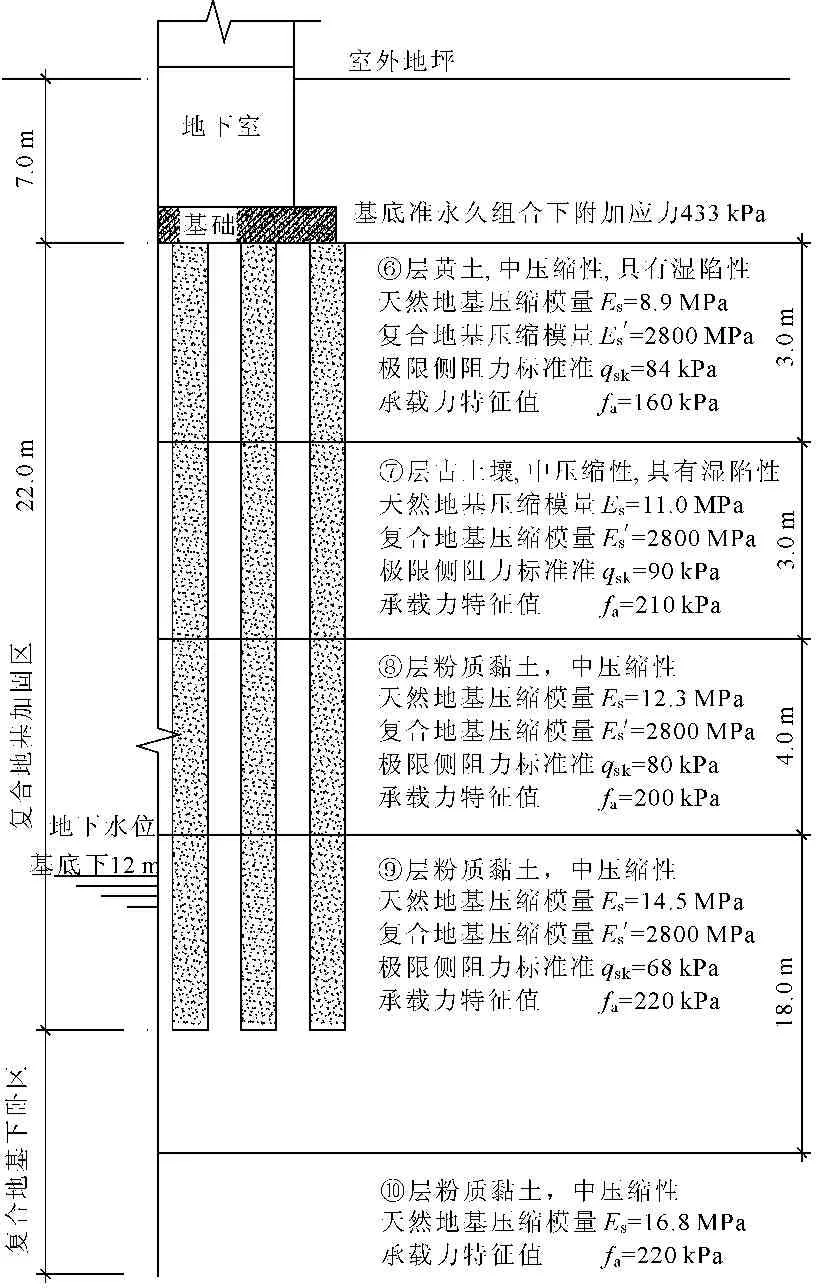
图2地基土分层剖面图

2.2沉降计算方法选取

根据本工程的实际情况，分别采用以下4种方法计算工程沉降变形。

2.2.1沉降变形统一算法一

选用常用的结构计算软件PKPM-JCCAD中的柔性筏板假定沉降计算法计算。沉降计算经验系数参照规范[13]中表5.3.5确定，采用式(3)确定复合地基复合压缩模量Espi，将各土层地质资料输入软件，程序自动将筏板划分为多个小的矩形筏板单元后，采用式(9)计算基础沉降。再对计算结果进行差值连接后得到整块筏板的沉降分布。图3给出了此种算法沉降的计算结果。

图3第一种沉降变形统一算法沉降计算结果

2.2.2沉降变形统一算法二

采用式(4)确定复合地基复合压缩模量Espi，其它沉降计算过程同算法一。软件计算后得到的沉降计算结果分布见图4。

图4第二种沉降变形统一算法沉降计算结果

2.2.3压力扩散法计算沉降量

采用此种方法计算时将基础等效为平面尺寸21 m×25 m的矩形基础。采用式(5)计算复合地基加固区内的压缩变形S1。采用式(7)的压力扩散法计算复合地基加固区底面的附加压力Pz，其中压力扩散角为30°。以压力扩散后的压力值及压力分布图形，采用式(6)计算复合地基下卧区压缩变形S2，式中计算经验系数取为1.0。继而采用式(1)得到总的沉降量S。应用压力扩散法计算图1所示28层建筑物沉降计算结果为55.0 mm。

2.2.4等效实体法计算沉降量

将复合地基加固区等效为21 m×25 m×22 m的实体基础，采用式(5)计算复合地基加固区内的压缩变形S1。采用式(8)的等效实体法压力扩散法计算复合地基加固区底面的附加压力Pz，其中选用勘察报告提供的CFG桩极限侧摩阻力标准值计算实体基础摩阻力。采用式(6)计算复合地基下卧区压缩变形S2，式中计算经验系数取为1.0。继而采用式(1)得到总的沉降量S。应用等效实体法计算图1所示28层建筑物沉降计算结果为60.1 mm。

3　实测沉降数据与计算沉降数据对比

本项目于2013年下旬封顶，经沉降观测，各楼的沉降速率稳定，且均无明显的不均匀沉降现象。图5给出了28层、33层各建筑物实测沉降与各计算方法得到的沉降计算结果的对比结果。从图5中可以看出：

(1) 28层的高层住宅实测平均沉降为31 mm左右，33层高层住宅实测平均沉降为37 mm左右，沉降数值基本接近此类工程剪力墙下单排布置钢筋混凝土长桩(35 m左右)的沉降观测数值。由于本工程设计中按照规范要求严格控制了筏板形心与结构重心的偏心率，各楼均未发生较为明显的不均匀沉降。由于本工程已经达到了普通高层建筑的高度限值，可以推测：在此类工程条件下，普通高层建筑的沉降均可控制在50 mm以内。

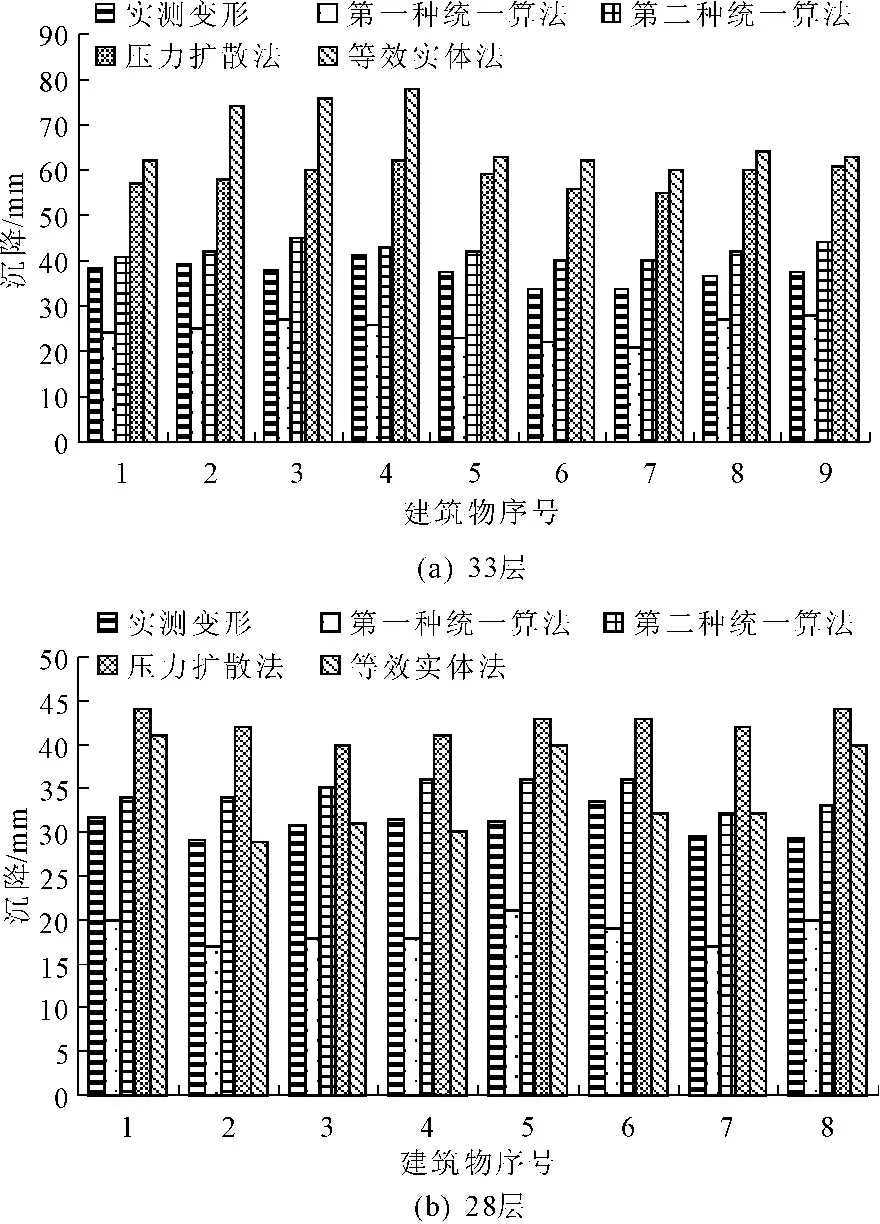
图5建筑物沉降结果对比分析

(2) 在与本工程相似的工程地质条件下，采用第一种统一算法的计算结果偏大，而第二种中统一算法与实测结果较为接近。工程设设计时应优先选用第二种统一算法。

(3) 等效实体法得到的沉降计算值偏差的离散性较大，产生这种差异主要是由于建筑物体型造成的。由于本方法只考虑加固区外围的摩阻力，当加固区体型较大时，计算摩阻力发挥作用小，得到的计算变形较大，反之得到的计算变形则较小。因此，此方法实用性不强。

(4) 本文应力扩散法计算时采用30°作为应力扩散角，得到的计算结果偏大。应力扩散法的计算结果与应力扩散角的选取有很大的关系，应力扩散角越大，得到的变形量通常越小。本文采用30°作为应力扩散角，经计算若公式(1)中沉降经验系数ψs1取0.7得到的沉降计算结果与实际沉降量较为相近。

4　结　论

在西安地区类似的复合地基设计时，对于复合地基的沉降，文中第二种统一算法的计算结果与实测沉降变形最为接近，且计算方法简单易行便于设计人员采用。文中压力扩散法所得到的计算结果虽然偏大，但结果稳定，偏于安全，且变异性小，适于对沉降变形计算结果进行复核检验，从而对建筑物沉降做出较为准确的预判。文中其他两种沉降计算方法，得到的计算结果与实测沉降结果对比不理想，在实际设计中不宜优先采用。

[1]沈伟，池跃君，宋二祥.考虑桩、土、垫层协同作用的刚性桩复合地基沉降计算方法[J].工程力学，2003，20(2)：36-42.

[2]池跃君，宋二祥，陈肇元.刚性桩复合地基沉降计算方法的探讨及应用[J].土木工程学报，2003，36(11)：19-23.

[3]杨光华，苏卜坤，乔有梁.刚性桩复合地基沉降计算方法[J].岩石力学与工程学报，2009，28(11)：2193-2200.

[4]Canetta G, Nova R. A numerical Method of analysis of ground improved by columnar inclusions[J]. Computers Geotech, l989,7(1):99-114.

[5]苏航州，段伟，段晓伟，等.水平荷载作用下GRF桩基础受力特性的数值分析[J].水利与建筑工程学报，2015，13(3)：200-204.

[6]李丽，鲍鹏，赵捷.刚性桩复合地基模型试验研究[J].建筑结构，2010，40(1)：69-71.

[7]鲍鹏，张惠，姜忻良.离散元法刚性桩复合地基承载机理研究[J].广东工业大学学报，2005，22(1)：105-109.

[8]池跃君，宋二祥，金淮，等.刚性桩复合地基应力场分布的试验研究[J].岩土力学，2003，24(3)：339-343.

[9]何春保，朱李春，李晓艺，等.刚性桩复合地基的设计与试验研究[J].广东工业大学学报，2009，26(1)：83-87.

[10]胡志.素混凝土桩复合地基试验研究及变形稳定性分析[D].重庆：重庆大学，2010：54-58.

[11]蒋明镜，周雅萍，朱方园.素混凝土桩复合地基承载机理的离散元分析[J].水利与建筑工程学报，2012，10(3)：1-7.

[12]中华人民共和国住房和城乡建设部.复合地基技术规范:GB/T50783-2012[S].北京：中国计划出版社，2012:15-19.

[13]中华人民共和国住房和城乡建设部.建筑地基基础设计规范:GB50007-2011[S].北京：中国建筑工业出版社，2011:26-31.

[14]龚晓南.复合地基理论及工程应用[M].2版.北京：中国建筑工业出版社，2007:128-132.

[15]中华人民共和国住房和城乡建设部.建筑地基处理技术规范:JGJ79-2012[S].北京：中国建筑工业出版社，2012:42-44.

Settlement of High Rise Building with Plain Concrete Pile Composite Foundation

WANG Chaonan1, HU Xiaopeng2, LIU Mingzhen2

(1.DesignInstitute,Xi'anUniversityofArchitectureandTechnology,Xi'an,Shaanxi710055,China; 2.SchoolofCivilEngineering,Xi'anUniversityofArchitectureandTechnology,Xi'an,Shaanxi710055,China)

In order to analyze the applicability of some composite foundation settlement calculation methods in Xi'an area, some settlement data of many high-rise buildings which applied plain concrete pile composite foundation were measured. Those settlement data and some calculation results which get from various composite foundation settlement calculation methods were compared and analyzed. The applicability of different calculation methods in similar engineering geological conditions was discussed. Some settlement experience coefficients of different calculation methods were proposed. The results show that similar composite foundation settlement calculation, the second unified algorithm is simple and its result is the closest to the measured settlement. The calculation result of the pressure diffusion method tends to be safe and the variation is smaller, the calculation method is suitable for the check of calculation results.

high-rise buildings; composite foundation ; settlement calculation; measured settlement

10.3969/j.issn.1672-1144.2016.04.014

2016-04-14

2016-05-01

国家自然科学基金资助项目(51308441)；陕西省教育厅专项科研计划项目(2013JK0951)

王超楠(1980—)，男，陕西西安人，硕士，工程师，主要从事建筑结构设计工作。 E-mail：shs339@sina.com

TU473

A

1672—1144(2016)04—0068—05