MGM （1，n） 模型在黔中枢纽大坝沉降分析的应用

庞先明，庞井龙，晏卫国，林志强

（1. 贵州省大坝安全监测中心，贵州 贵阳 550002；2. 福建省建筑科学研究院，福建 福州 350024）

MGM （1，n） 模型在黔中枢纽大坝沉降分析的应用

庞先明1，庞井龙1，晏卫国1，林志强2

（1. 贵州省大坝安全监测中心，贵州 贵阳 550002；2. 福建省建筑科学研究院，福建 福州 350024）

岩溶地区影响高面板坝施工期和初运行期沉降变形的不利因素较多，沉降变形是一个复杂的非线性系统过程。灰色理论能从有限的、离散的数据中寻求潜在的必然性，因而较适合于岩溶地区高面板坝的沉降变形分析。针对单点 GM（1，1）模型不能考虑沉降监测点间的关联性，反映不出高面板坝整体变形规律的问题，在灰关联分析的基础上，选取黔中水利枢纽工程高面板坝施工期坝体最大沉降测点及与其关联性较大测点的观测数据建立空间多变量灰色预测模型 MGM（1，3）模型。计算结果表明，与单点 GM（1，1）模型相比，MGM （1，3）模型能反映出高面板坝沉降的整体变形规律，且模型的模拟和预测精度高。

黔中水利枢纽工程；沉降分析；面板堆石坝； MGM（1，n）模型；沉降变形

0　引言

黔中水利枢纽工程是一项以灌溉、城乡供水为主，兼顾发电等综合利用，并为改善区域生态环境创造条件的大型水利基础设施项目。该工程位于喀斯特地貌广泛分布的云贵高原，坝址位于 V 型峡谷河段（河床宽高比 2.18），两岸山体雄厚，岩溶较为发育。水库总库容 10.89 亿m3，正常蓄水位为 1 331.00 m，属大（I）型工程。拦河坝为混凝土面板堆石坝，筑坝材料大部分为新鲜或微风化岩石，少部分为弱风化岩石。大坝趾板建基面高程为 1 178.0 m，坝顶高程为 1 335.0 m，最大坝高为 157.0 m，坝顶长为363.0 m，宽为 10.6 m，上游坝坡（面板下游侧）为1∶1.400，下游平均坝坡为 1∶1.536［1］。

针对黔中水利枢纽面板堆石坝坝址处地形、地质条件及筑坝材料等的特点，大坝设置了变形、渗流、应力应变等监测项目。根据坝体内部水管式沉降仪实测施工期堆石体沉降成果建立模型，寻找坝体的沉降变形规律，对于检查坝体填筑质量和寻找面板混凝土浇筑的最佳时机具有重要的指导意义。目前常用的土石坝沉降变形分析方法有回归分析法、时间序列分析法、灰色理论法、BP 神经网络法、遗传算法等［2-3］。岩溶地区影响高面板坝沉降变形的不可预见因素较多，而灰色理论分析是将系统的主行为数据看作是所有行为因子作用的综合结果，从有限的、离散的数据中寻求潜在的必然性，通过灰关联分析提取因子建立模型，因而灰色理论方法较适合于岩溶地区高面板坝的沉降变形分析。目前常用的 GM（1，1）模型采用单个监测点建模和预测，只是对监测对象局部变形的研究。实际上，面板坝沉降变形监测点间的变形并非孤立，每个沉降变形监测点既影响着其它监测点的变形，又受到其它沉降监测点变形的影响［4］。因此从面板坝整体的角度描述沉降变形的规律和趋势，建立空间多变量灰色预测模型（Multi-variable Grey Model，记为MGM（1，n））。

1　MGM（1，n）模型求解和建模步骤

MGM（1，n）是单测点 GM（1，1）模型在多点情形下考虑测点间相关性的动态关联分析模型，参数能够反映变量间的相互影响，适合对系统做整体、动态的分析［5］。

1.1灰关联分析

建立 MGM（1，n）模型前首先要进行相关性分析，以检验纳入模型的各变量间是否存在相互影响和制约关系，从而选取相关性大的变量序列进行建模和预测［6］。

令 x'0（k） = x0（k）/max （x0（k）） ，x'j（k） = xj（k）/max （xj（k）），则参考序列 x0与比较序列 xj在 k 点的灰色关联系数表示为

式中：ξj（k） 为灰色关联系数；ρ 为分辨系数，取值范围为 ［0，1］，一般取 0.5。

取各点的灰色关联系数的平均值作为比较序列xj对参考序列 x0的灰色关联度 rj，则

一般当 rj≥0.5 时即可认为比较序列与参考序列有较好的关联性，rj越大，比较序列和参考序列的关联性越大，序列之间的联系就越紧密。

1.2MGM（1，n）模型原理［7-8］

方程组的矩阵形式为

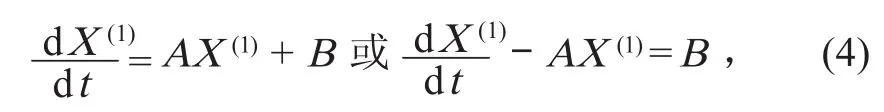
式中：A 和 B 为辨识参数，值为

整理后得连续时间响应为

1.3MGM（1，n）模型求解

1.3.1求辨识参数 A 和 B

参数 A 和 B 可以通过最小二乘法则计算得到：

式中：

1.3.2预测模型

MGM（1，n）模型的计算值为

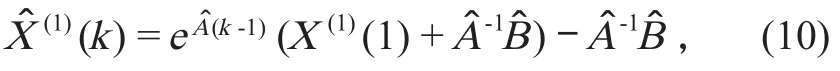
还原预测模型为

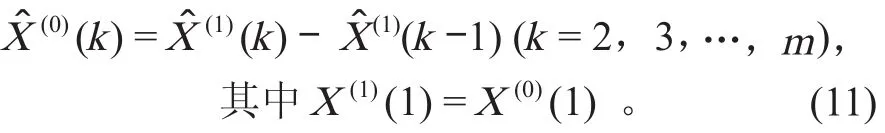
1.3.3模型检验

模型残差平方和 σ2为

式中：残差向量 Vi（k） 为

1.4MGM（1，n）建模具体步骤

本 MGM（1，n）模型的建模计算过程采用Matlab 编程实现。Matlab 内置的大量方便易用的函数和文件及其面向对象的编程特点，使得建模过程变得简便易行。具体建模步骤如下：

1）构成原始数据序列 X（0）；

2）计算 X（0）的一次累加生成序列 X（1）；

3）构造生成背景值序列 Z（1）；

4）按式（8）和（9）构造矩阵 L 及列阵 Y；

5）按式（7）进行矩阵运算得模型参数：

6）按式（6）求 eAT；

8）计算残差并检验模型精度。

2　MGM（1，n）建模步骤与实例

2.1观测数据处理

黔中水利枢纽工程于 2011 年 11 月 30 日动工，2015 年 4 月 14 日下闸蓄水，已取得施工期较完整的观测资料［1］。根据施工期坝体沉降监测成果，黔中水利枢纽工程的最大沉降量发生在最大断面坝横0-7.50 m 的 1 242.00 m 高程的坝轴线 SG13 测点处，与国内外同类工程相比较，沉降量和变形规律属正常。本研究选取施工期最大断面坝横 0-7.50 m 的1 242.00 m 高程的沉降监测数据建立 MGM（1，n）模型，建模与计算采用 Matlab 编程实现。

灰色理论分析方法是基于等时间间隔数据序列建立模型进行拟合预测的，受施工状况及天气等因素的影响，大坝的监测往往不是等时间间隔的。因此首先应对原始数据进行等时距处理，然后根据等时距数据序列建立模型。本研究采用线性内插值法处理得到 7 d 等时间间隔的数据序列建立模型。最大断面坝横 0-7.50 m 内部沉降测点布置如图 1 所示。

图1　黔中水利枢纽最大断面坝横 0-7.50 m 内部沉降测点布置图

2.2灰关联分析

将 1 242.00 m 高程的 SG10～SG16 沉降变形监测点依次作为灰关联分析的参考序列，而将其余序列作为比较序列进行灰关联分析，各点的灰色关联度如表 1 所示。可以看出 SG13 测点与其余 6 个测点的灰色关联度均 ＞ 0.5，表明其与各测点之间的沉降变形有较好的关联性；随着距离的增加，各测点与SG13 测点的灰色关联度逐渐减小，表明距离越近的测点与 SG13 测点之间沉降变形的关联性越紧密。

2.3模型计算结果分析

根据灰关联分析结果，分别选取各个沉降测点的前 8 期监测数据建立 MGM（1，7）模型（SG1～SG16），MGM（1，5）模型（SG11～SG15）及MGM（1，3）模型（SG12～SG14）拟合和预测SG13 测点的沉降量，发现只有 MGM（1，3）模型效果最好。选取相同期数的 SG13 测点监测数据建立GM（1，1）模型作为对比。

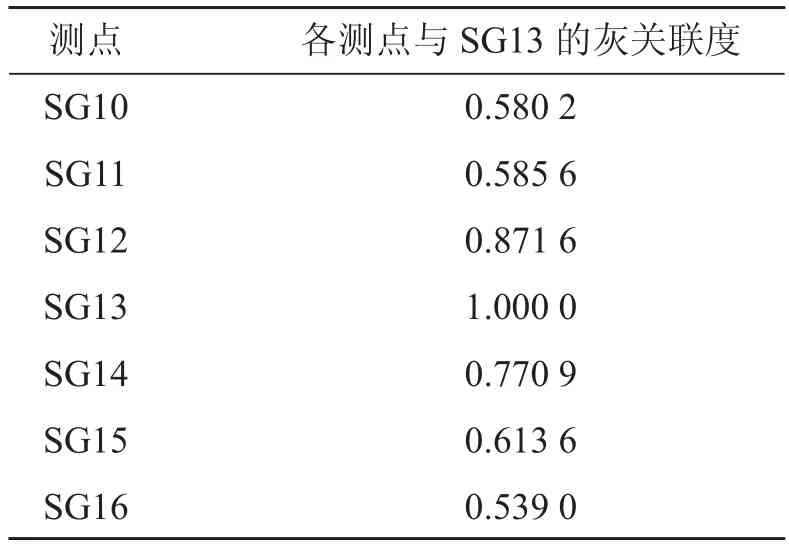
表1　测点灰关联度检验表

选取 SG12～SG14 监测点的前 8 个数据序列建立 MGM（1，3）模型，计算 3 个测点的一次累加生成序列 X（1）为

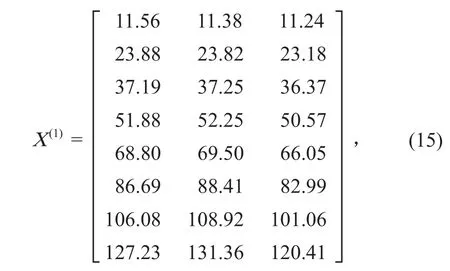
因此 3 个变量的一次累加生成序列微分方程为

SG13 测点的实测值与 MGM（1，3），GM（1，1）2 个模型的拟合预测值对比如表 2 所示，实测值和模拟预测值过程线如图 2 所示。

表2　SG13 测点不同模型拟合预测值对比表

图2　SG13 测点 GM（1，1），MGM（1，3）模型拟合预测值与实测值对比图

从表 2 和图 2 可以看出：从拟合效果来看，MGM（1，3）模型能够考虑测点间的关联影响，对沉降数据序列的拟合精度要高于单测点 GM（1，1）模型；从预测效果来看， MGM（1，3）模型的中长期预测精度较高，而单测点 GM（1，1）模型并不适用于非指数增长的数据序列的预测。

灰色多变量 MGM（1，n）模型保留了灰色模型处理贫信息的特点，同时考虑系统中因素间的相互关联性，适用于对具有非线性系统特征的岩溶地区高面板坝施工期的沉降变形分析。此模型可以根据施工期堆石体少量的沉降变形监测数据建立模型，及时有效地反映堆石体的最大变形量和变化规律，便于检查施工质量和指导面板浇筑。但合理有效的MGM（1，n）模型存在一个纳入模型的最佳点位数，漏掉与之关联性大的测点或者多考虑与之关联性小的测点，会使模型精度下降甚至失真。

3　结语

本研究在灰关联分析的基础上，选取关联度大的测点数据序列舍弃关联度小的测点数据序列，建立的高面板坝施工期沉降变形的 MGM（1，3）模型拟合预测效果良好，能很好地反映测点沉降变形的发展趋势，对于检查坝体填筑质量和寻找面板施工的最佳时机具有重要的指导意义，在工程实践中具有良好的应用价值。

但是 MGM（1，n）模型的模拟预测精度与模型容纳测点的数量有较大关系，存在一个合理的模型测点数，此测点数能包含所有与之关联性大的测点，而剔除与之关联性小的测点。因此，如何选取合适的测点数建立合理有效的 MGM（1，n）模型是今后值得研究的一个问题。

［1］ 庞先明，晏卫国. 黔中水利枢纽一期工程水源枢纽施工期大坝观测资料分析阶段性报告［R］. 贵阳：贵州省大坝安全监测中心，2013: 5-15.

［2］ 汪树玉，刘国华，刘立军，等. 观测数据分析中几种方法的探讨（一）回归—时间序列模型和贝叶斯预测模型［J］.水电自动化与大坝监测，2003，27 （2）: 43-46.

［3］ 汪树玉，刘国华，刘立军，等. 观测数据分析中几种方法的探讨（二）整体分析与多变量灰色模型［J］. 水电自动化与大坝监测，2003，27 （3）: 59-62.

［4］ 刘国华，何勇兵，汪树玉. 土石坝沉降预测中的多变量灰色预测模型［J］. 水利学报，2003 （12）: 84-88.

［5］ 刘寒冰，向一鸣，阮有兴. 背景值优化的多变量灰色模型在路基沉降预测中的应用［J］. 岩土力学，2013 （1）: 173-181.

［6］ 顾冲时，吴中如. 大坝与坝基安全监控理论和方法及其应用［M］. 南京：河海大学出版社，2006: 123-136.

［7］ 王穗辉，潘国荣. 基于 MATLAB 多变量灰色模型及其在变形预测中的应用［J］. 土木工程学报，2005 （5）: 24-27.

［8］ 刘思峰，杨英杰，吴利丰. 灰色系统理论及其应用［M］.北京：科学出版社，2014: 255-259.

Application of MGM（1，n） Model in Settlement Analysis of Qianzhong Hydraulic Dam

PANG Xianming1， PANG Jinglong1， YAN Weiguo1， LIN Zhiqiang2
（1. Guizhou Provincial Dam Safety Observation Center， Guiyang 550002， China；2. Fujian Provincial Academy of Building Research， Fuzhou 350024， China）

Karst areas have much more unfavorable factors on high concrete rockfill dam settlement during the constructing and initial operating period. Settlement is a complex nonlinear systematic process. By extracting potential inevitability from the finite and discrete settlement data， grey system theory suitable for dam settlement deformation analysis of the high concrete face rockfill dam in karst areas. The single point model named GM（1，1） can’t consider the correlation of settlement between the discrete monitoring points and can’t respect the integrated deformation regularity of the high concrete rockfill dam settlement. Based on grey correlation analysis， the MGM（1，3） model is established in this paper using the settlement data of the maximum and its relating monitoring points of the Qianzhong hydraulic project dam during the constructing period. A case study shows the MGM（1，3） model can respect the integrated deformation regularity of the high concrete rockfill dam settlement and has a higher precision in simulating and forecasting than GM（1，1） model.

Qianzhong hydraulic project； sedimentation analysis； high concrete rockfill dam； MGM（1， n）；settlement

TV64

A

1674-9405（2016）04-0015-05

10.19364/j.1674-9405.2016.04.004

2016-04-01

贵州省重大科技专项计划项目（20126013-2）

庞先明（1974- ），男，贵州道真人，高级工程师，从事水利水电工程安全监测工作。