基于蜻蜓算法和支持向量机的变压器故障诊断

傅军栋，陈　俐，康水华，冯奕轩

（华东交通大学电气与自动化工程学院，江西 南昌330013）

基于蜻蜓算法和支持向量机的变压器故障诊断

傅军栋，陈俐，康水华，冯奕轩

（华东交通大学电气与自动化工程学院，江西 南昌330013）

电力变压器作为电力系统中变换电压、输送电能、分配电能的重要电力设备，其运行状态直接影响到电网的运行安全。为了提高故障诊断的准确率，提出了一种基于蜻蜓算法（dragonfly algorithm，DA）和支持向量机（support vector machine，SVM）的变压器故障诊断方法。利用蜻蜓算法DA对SVM分类器参数进行优化且以SVM分类预测准确率最大为其适应度函数。变压器故障诊断实例仿真结果分析表明：基于蜻蜓算法的DA-SVM支持向量机的变压器故障诊断与交叉验证法CV-SVM，基于遗传算法的GA-SVM，基于粒子群算法的PSO-SVM相比较，在变压器故障诊断中具有故障诊断准确率高，全局寻优能力强，收敛速度快，且稳定性好的优越性。

蜻蜓算法；支持向量机；变压器；故障诊断

电力变压器是电力系统的关键设备，正确诊断电力变压器的潜伏性故障对提高电力系统的运行安全性、可靠性及经济性具有重要意义［1-4］。

由于油浸式变压器油中溶解气体的组成与含量可以在很大程度上反映变压器的运行状态，国际电工委员会推荐油中溶解气体分析方法（dissolved gas analysis，DGA）已经成为油浸式变压器故障诊断的一种最方便，有效方法之一［5］。它能比较准确、可靠的发现变压器潜伏性故障，从而防止重大事故的发生。目前，故障判断的方法主要有三比值法、Rogers法、Dornerburg法以及改良三比值法等传统方法以及人工神经网络、叶贝斯网络、支持向量机等智能方法。但是传统方法在实际应用中存在编码缺失以及编码界限过于绝对等问题［6-7］；人工神经网络则存在过拟合和易陷于局部最优，其精度难以得到保证；叶贝斯网络则需要大量的数据样本［8-9］。而支持向量机（support vector machine，SVM）分类器是在统计学习理论基础上发展起来的一种新的学习方法，它采用结构风险最小化原则，具有很强的泛化能力，可以有效解决小样本、过拟合、非线性及高维模式识别等问题，在变压器故障诊断中有着很好的应用前景［10］。而支持向量机（SVM）参数的选取对其分类准确率有着重要影响［11-15］。蜻蜓算法（DA）作为一种新兴的元启发式智能算法，有较强的稳定性，较好的寻优速度及全局寻优能力等优点。就蜻蜓算法的这些优点，提出一种基于蜻蜓优化算法（DA）的SVM参数寻优方法，来对向量机的核参数和惩罚因子进行优化选择，再利用优化得到的支持向量机模型，诊断油浸式变压器故障。为了说明该方法在变压器故障诊断中是有效的，将运行时间t、分类器准确率F-Accuracy，诊断模型准确率Accuracy及稳定性与传统的交叉验证法CV-SVM变压器故障诊断，基于遗传算法的GA-SVM变压器故障诊断，基于粒子群算法的PSO-SVM变压器故障诊断的相应数据来对比。变压器故障诊断实例结果分析表明：本文提出的基于蜻蜓算法和支持向量机DA-SVM变压器故障诊断方法，在SVM分类器的参数组合（C，g）寻优中，较其他3种算法所耗费时间少，寻优能力强，变压器故障诊断的准确率高，稳定性好，且收敛性好，收敛速度快［16-17］。

1　算法原理

1.1SVM算法原理

支持向量机最初是研究线性可分问题而提出的，设一个具有l个训练样本集｛（xi，yi），i=1，2，…，l｝，引入松弛变量ξi，则最优分类超平面可以描述为

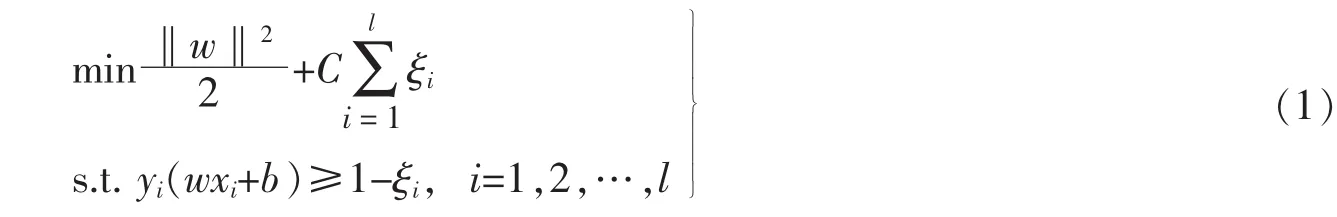
式中：w为权值向量；‖w‖2为w的欧拉范数；b为偏差；wxi表示内积；w和b可以通过求解Largrange函数的鞍点得到，即

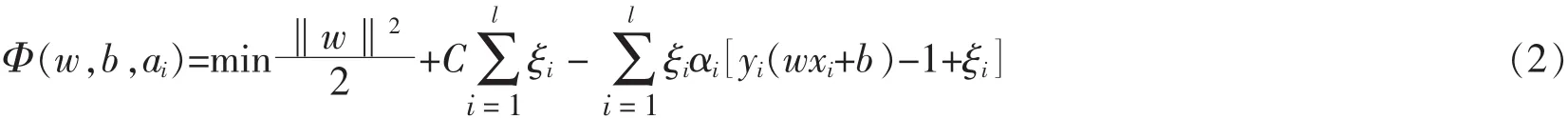
式中：αi＞0，i=1，2，…，l为Largrange系数。

由于在实际应用中，绝大多数是非线性的，因此将原输入空间的样本映射到高维的特征空间H中，再在高维的特征空间H中构造最优分类超平面。Vapnik等人提出满足Mercer条件的核函数K（xi，xj）来代替内积运算，即得到式（3）

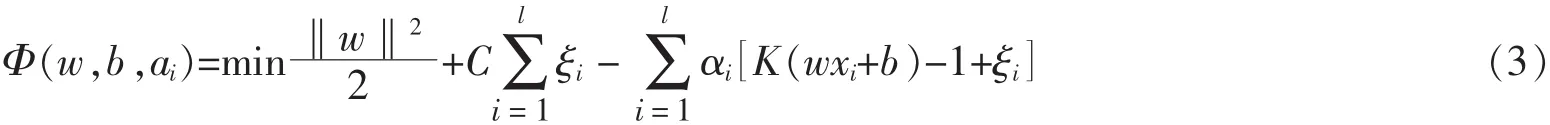
由于式（3）计算复杂，几乎不能直接求解；因此将其转化为对偶问题：

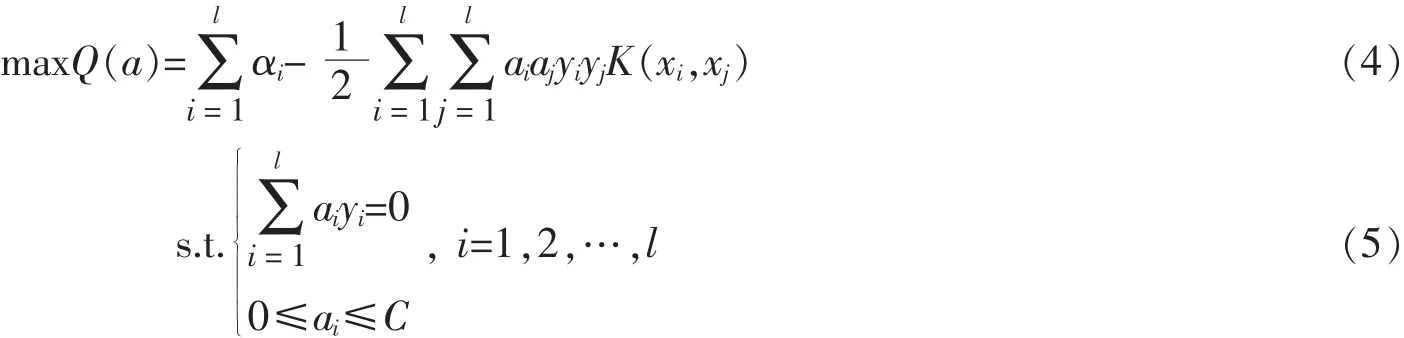
从而最终的最优分类函数

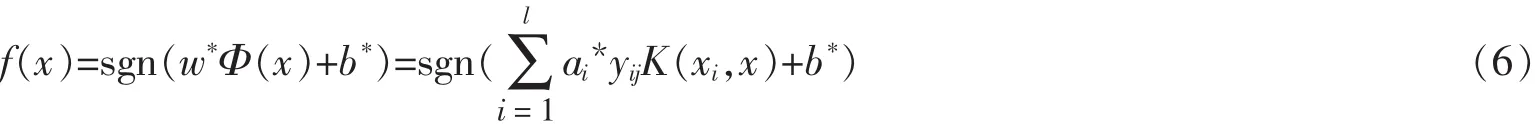
式中：a*，w*和b*为式（4）用二次规划法求得的最优解，其中常用的核函数有线性核函数、d阶多项式核函数、径向基核函数（高斯核函数）和具有参数k和θ的Sigmoid核函数［10，12-13，17］。

核函数的选择对支持向量机的性能有着重要的影响，本文选用运用广泛，适应性广的径向基核函数。径向基核函数可以处理类标和属性之间的关系，且需要确定的参数只有一个，模型的建立相对简单，其表达式如下所示：

而惩罚因子C和核参数g的选取，对模型影响较大；因此文章第3部分将结合蜻蜓算法对核参数寻优。

1.2DA算法原理

蜻蜓是一种小型食肉动物，其独特的群体行为捕食和迁徙，吸引着科学家的注意，捕食称作静态群行为，迁徙称作动态群行为。在静态群行为期间，蜻蜓分作小群体，在一个小区域来回飞行，捕食蝴蝶和蚊子，而在动态群行为期间，大量的蜻蜓组成群体进行远距离地迁徙。这2种行为与元启发式算法的探索和发现2个重要阶段非常相似；因此，SeyedaliMirjalili运用数学方法模拟了蜻蜓这2种群行为，在2015年提出一种新型的群智能算法——蜻蜓算法（dragonfly algorithm，DA）［14］。

研究表明，任何种群行为都遵循3个基本准则：分离（separation）、对齐（alignment）和内聚（cohesion）。分离是指避免个体与相邻个体的静态碰撞；对齐是指个体与相邻个体保持一致的速度；内聚是指个体倾向于向相邻个体的中心聚拢。而所有的动物为了生存，本能地靠近食物源、远离天敌；因此，个体位置的更新与下面5种行为有关，数学方法表达如下。

1）分离度

式中：X表示当前蜻蜓个体的位置；Xj表示第j个相邻蜻蜓个体的位置；N表示与第i个蜻蜓个体相邻的x个体数量。

2）对齐度

式中：Vj表示第j个相邻蜻蜓个体的速度；N表示与第i个蜻蜓个体相邻的个体数量。

3）内聚度

4）食物吸引力

式中：X+表示食物源位置。

5）天敌排斥力

式中：X-表示天敌位置。

因此根据上述5种蜻蜓行为，下一代蜻蜓的位置和位置更新步长计算如下：

式中：t表示当前迭代次数；i表示第i个蜻蜓个体；Xt表示当前t代种群个体位置；△Xt+1表示下一代种群位置跟新步长；Xt+1表示下一代种群个体位置；s表示分离度权重；Si表示第i个个体的分离度；a表示对齐度权重；Ai表示第i个个体的对齐度；c表示内聚度权重；Ci表示第i个个体的内聚度；f表示食物因子；Fi表示食物位置对第i个个体的吸引力；e表示天敌因子；Ei表示天敌位置对第i个个体的排斥力；w表示惯性权重。

由式（14）可知，相邻个体的数量对蜻蜓种群的步长和位置更新有很大的影响，而个体之间满足什么样的条件才是相邻呢？为了解决这个问题，Seyedali Mirjalili假设每个蜻蜓个体都是处于半径为r的圆的圆心，如果个体i与个体j之间的欧氏距离小于r，则认为个体i与个体j相邻，为了加快收敛速度，半径r随着迭代次数的增加而增加。当没有任何个体与个体i相邻时，为提高蜻蜓搜索时的随机特性，引入Lévy flight随机游走方法。Lévy flight命名自法国数学家Paul Lévy，是一种Markov过程，行走的步长满足一个heavytailed的Lévy分布，计算如式（15）：

式中：r1，r2是［0，1］之间的随机数；β是一个常量（此处为3/2）；σ计算如式（16）：

因此，没有任何个体相邻时，种群位置更新如式（17）：

1.3基于蜻蜓算法DA优化SVM参数

核函数的选择对支持向量机的性能有着重要的影响，径向基核函数不管是高维数据还是低维数据都具有良好的收敛域，且适应性较好；因此，本文选用适应性广的径向基核函数作为SVM分类预测的核函数。影响径向基核函数支持向量机分类性能的主要参数为：惩罚参数C和核参数g。蜻蜓算法将群体行为的所有可能因素（分离，对齐，内聚，食物吸引，天敌排斥及位置的随机游走）都考虑在内，使其能够快速的在最优值附近收敛，且具备良好的全局寻优能力和稳定性。基于上述优点，将其应用于支持向量机的参数寻优中，在保证SVM分类准确率达到最大的情况下，寻找最适合的惩罚参数C和核参数g。基于蜻蜓算法的SVM参数寻优步骤如下。

Step 1初始化参数设置。蜻蜓算法主要参数设置有：蜻蜓的个数、蜻蜓最大迭代次数；支持向量机主要参数设置有：惩罚参数C和核参数g的上下限值ub，lb。

Step 2设置支持向量机相应数据集。按相同的比例设置相应的数据集，主要设置的数据集有：训练集train、训练数标签train_labels、测试集test和测试集标签test_labels。

Step 3初始化蜻蜓。蜻蜓位置初始化X、位置变化步长初始化△X，将参数组合（C，g）设为每只蜻蜓要为SVM优化的组合，其中X矩阵的第一行存放惩罚参数C的值，X矩阵的第二行存放核参数g的值；根据Step 1中惩罚参数C和核参数g的取值范围随机初始化蜻蜓。

Step 4计算各权重值。根据Step 1中的初始值，随机初始化初始相邻半径r，惯性权重w，分离度权重s，对齐度权重a，内聚度权重c，食物因子f，天敌因子e。

Step 5计算适应度值。根据训练集train和训练集标签train_labels训练支持向量机模型，并将该模型用于目标集test和目标标签集test_labels的分类预测中，将支持向量机的分类准确率作为每只蜻蜓当前的适应度值，蜻蜓每进行一次行为操作，便计算一次当前蜻蜓的最大适应度值：若有当前蜻蜓的适应度值大于已保存的适应度值，则用当前的蜻蜓的适应度值替代原保存的最优适应度值，并将较优作为当前蜻蜓的最优值，并保存当前最优值所对应的蜻蜓的参数组合（C，g），否则仍保存原适应度值及其所对应的蜻蜓参数组合（C，g）。

Step 6寻找是否存在相邻蜻蜓。利用欧氏距离判断蜻蜓与蜻蜓间是否存在相邻蜻蜓。若存在，位置更是计算使用公式（14），若不存在，位置更新使用公式（17）。

Step 7计算各蜻蜓行为度。根据公式（8）—（12）分别计算各蜻蜓的分离度S、对齐度A、内聚度C、食物吸引力F、天敌排斥力E。

Step 8位置更新。根据Step 6更新蜻蜓的位置及根据公式（13）计算步长。

Step 9判断是否满足算法的终止条件：判断是否达到预设的蜻蜓最大迭代次数 ，若是则输出蜻蜓的最大适应度值和最优值所对应的蜻蜓的参数组合（C，g），否则迭代次数加 1，并跳转执行Step 4。

基于蜻蜓算法的SVM参数寻优的流程图如图1所示。

图1　DA-SVM流程图Fig.1　Process of optimizing the SVM parameters with DA

2　基于DA-SVM的变压器故障诊断模型

2.1评价指标的选取和量化

根据《油浸式变压器（电抗器）状态评价和检修导则》，本文采用油色谱数据（DGA）中的H2，CH4，C2H4，C2H6，C2H2，CO和CO2气体含量占总烃的比值作为故障判断的特征变量［1-2，15］。将变压器的故障分为：低温过热、高温过热、低能放电、高能放电、放电兼过热5个类型。其具体特征变量及故障类型举例见表1。因不同变压器里面的气体含量不同，为了更好的训练，识别以及提高其诊断效果，本文将收集到的油色谱数据中的各项气体相对含量进行归一化处理，再作为支持向量机模型的输入，利用典型故障气体的相对含量在高维空间的分布特性进行变压器故障类型诊断［18］。

表1　油中溶解气体含量举例Tab.1　Content of gases dissolved in transformer oil PPm

其中故障类型1表示低温过热；故障类型2表示高温过热；故障类型3表示低能放电；故障类型4表示高能放电；故障类型5表示放电兼过热。

2.2建立变压器故障诊断模型

本模型选用LIBSVM作为训练和测试工具，选用RBF核函数作为核函数，将进行归一化处理后的气体的相对含量作为输入，各故障类型所对应的编码作为输出。在参数寻优时，利用传统的交叉验证CV-SVM，基于遗传算法的GA-SVM参数寻优法，基于粒子群算法的PSO-SVM参数寻优法及本文提出的基于蜻蜓算法和支持向量机DA-SVM变压器故障诊断方法分别对支持向量机进行参数组合（C，g）寻优，最终得出模型拟合度最好的参数组合（C，g），根据参数建立模型。

3　变压器故障诊断实例分析及比较

3.1实例数据

考虑到变压器的容量、型号、环境等因素的影响，本文从某省电力公司收集到了大量具有明确结论的变压器（220 kV）油色谱数据，剔除冗余样本和一些奇异数据后，最终选择了500组样本。将各类故障类型样本随机平均分成2组：训练集、测试集，其具体训练集和测试集划分如表2。

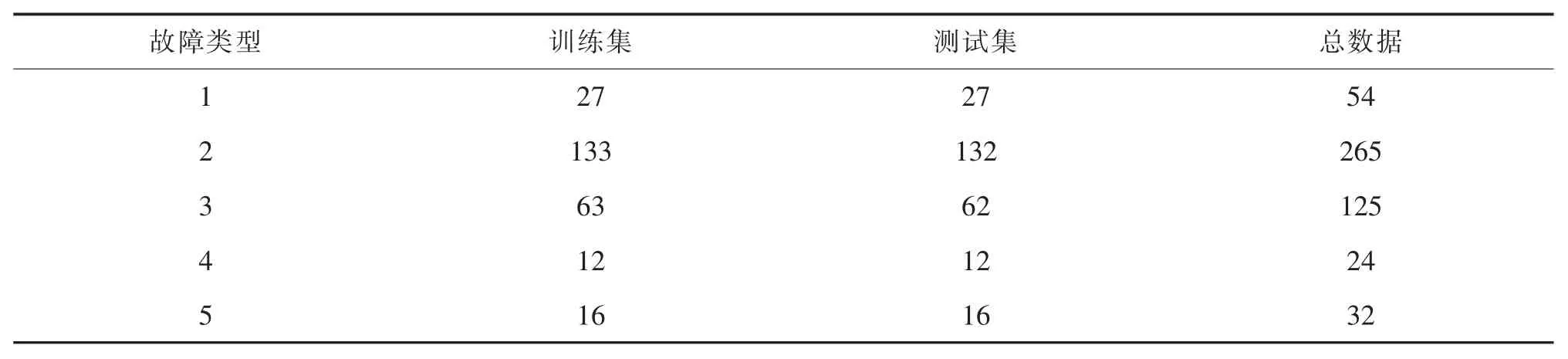
表2　各数据集Tab.2　Each data set

3.2各算法参数设置

在CV-SVM交叉验证法时限定惩罚参数C取值范围（0，100］，高斯核参数g的取值范围（0，100］，步长设置均为0.01；各元启发式智能算法GA-SVM，PSO-SVM，DA-SVM中，种群的最大迭代次数为200，种群规模为20，惩罚参数C范围（0，100］，核参数g范围（0，100］；其中GA-SVM中交叉概率取0.7，变异概率为0.01；PSO-SVM中更新速度c1取1.494 45，更新速度c2取0.5，粒子最大速度取0.5，最小速度取-0.5；DA-SVM无需另外再进行参数设置。

3.3各算法运行结果及分析

分别将上述4种方法以及所收集的变压器油色谱数据运用到对SVM分类器参数进行优化，选取最优参数组合（C，g），并利用各方法寻优所寻得的最优参数组合（C，g）及SVM分类器用对所收集的变压器油色谱数据进行预测，通过对其相应的运行时间t、分类器准确率F-Accuracy，诊断模型准确率Accuracy、最佳惩罚参数best C及最佳核参数best g来评价其相应的性能。

将上述各算法依次运用到变压器油色谱数据中，各运行10次，将其各组数据依次记录在表3中。其各个算法寻优过程见图2-图4。其各个算法对变压器油色谱数据的分类效果图依次为图6-图9。

表3　各算法参数C，g和准确率Tab.3　Algorithm parameters C，g and accuracy

其各个算法寻优图依次为

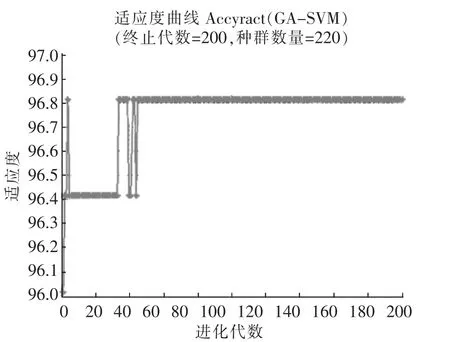
图2　GA-SVM寻优图Fig.2　Optimization figure of CV-SVM

图3　PSO-SVM寻优图Fig.3　Optimization of PSO-SVM

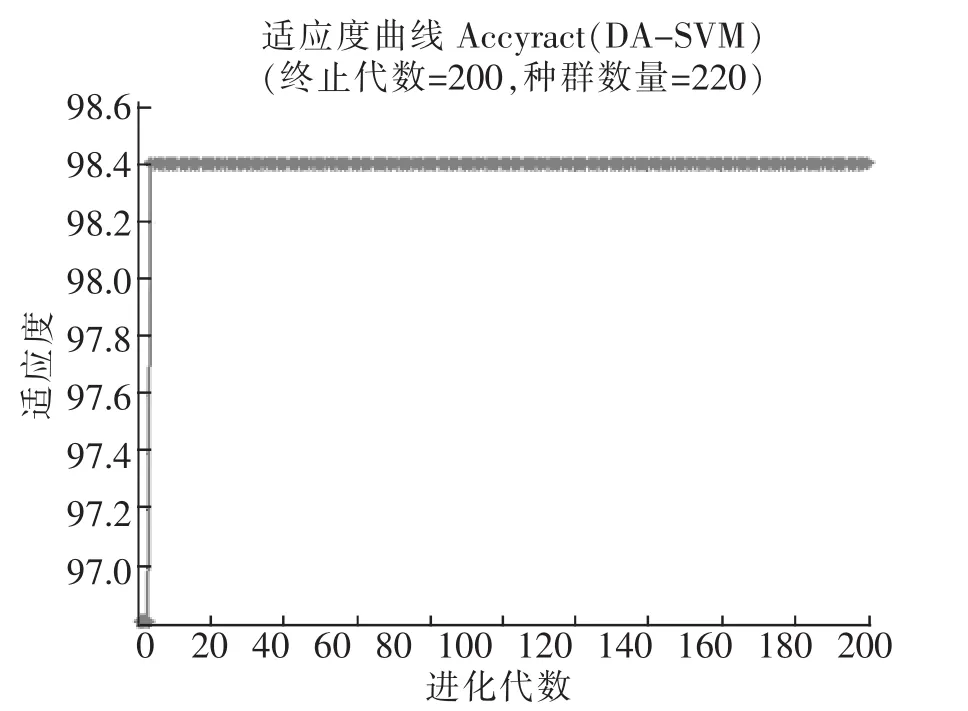
图4　DA-SVM寻优图Fig.4　Optimization of DA-SVM

其各个算法变压器故障诊断分类预测图依次为

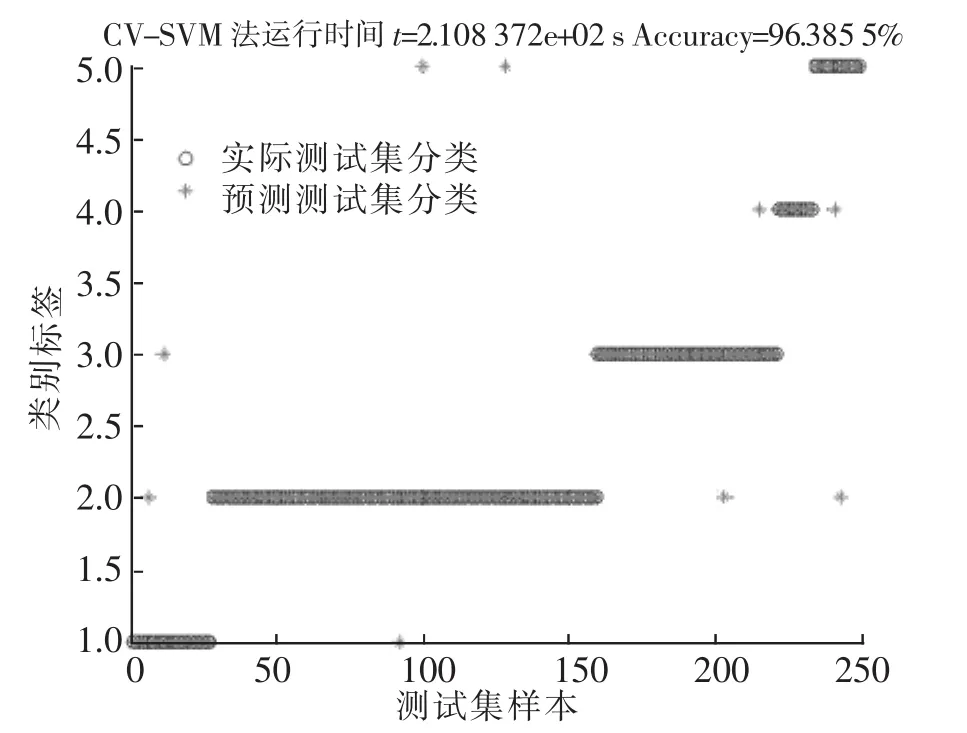
图5　CV-SVM变压器故障诊断分类效果图Fig.5　Fault diagnosis classification effect of CV-SVM

图6　GA-SVM变压器故障诊断分类效果图Fig.6　Fault diagnosis classification effect of GA-SVM

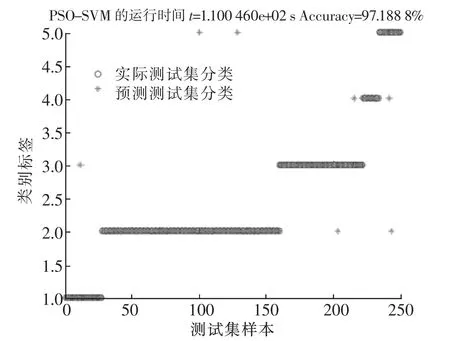
图7　PSO-SVM变压器故障诊断分类效果图Fig.7　Fault diagnosis classification effect of PSO-SVM

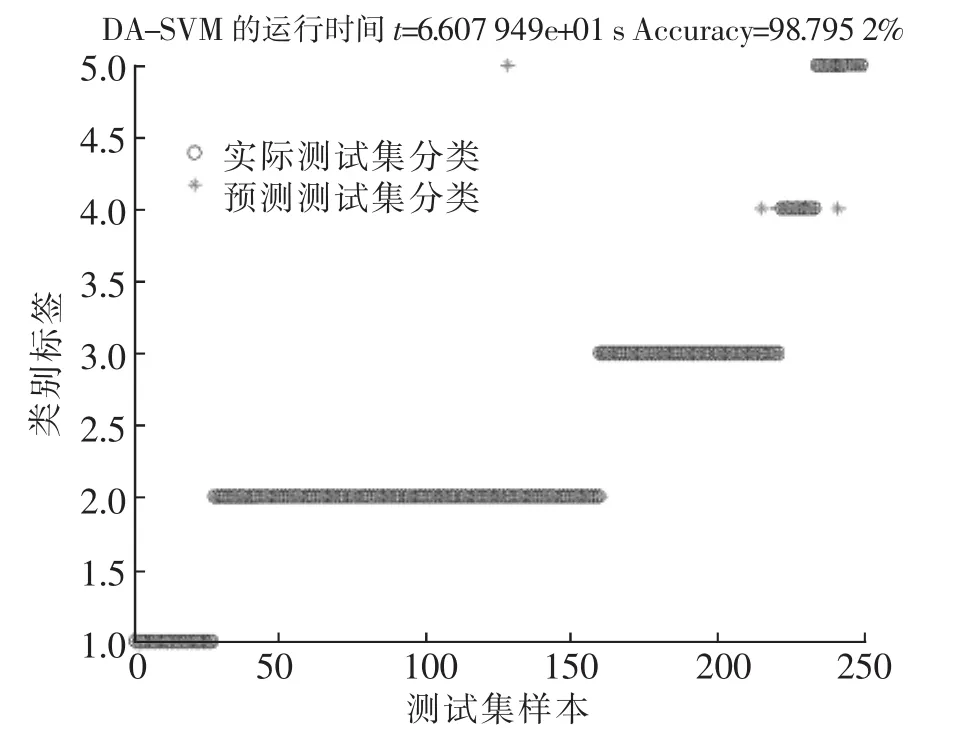
图8　DA-SVM变压器故障诊断分类效果图Fig.8　Fault diagnosis classification effect of DA-SVM

表4　各算法参数C，g和准确率汇总Tab.4　Algorithm parameters C，g，and accuracy summary

将表3中时间t，分类器准确率F-Accuracy及变压器诊断准确率Accuracy取平均值，惩罚参数和核参数的组合选择惩罚参数较小的参数组合，将其汇总到表4。

由表4及图2-图8可得出：通过对变压器油色谱数据的分析处理，分别采用4种不同的算法对支持向量机的SVM分类器的参数组合（C，g）进行寻优。从变压器故障诊断的数据及图形分析可得，本文提出的基于蜻蜓算法的支持向量机DA-SVM的变压器故障诊断，与传统的交叉验证法支持向量机CV-SVM变压器故障诊断、基于遗传算法的支持向量机GA-SVM变压器故障诊断及基于粒子群算法的PSO-SVM变压器故障诊断相比，在寻找参数组合（C，g）时有更高的分类器准确率及更高的变压器故障诊断准确率，更强的寻优能力，更好的收敛性及收敛速度，且具有较良好的稳定性。由图2-图4图中可以看出，图2、图3在达到最优前容易陷入局部最优，而图4则没有这种情况，因为蜻蜓算法的位置更新的5种行为可以避免搜索陷入局部最优的情况。传统的交叉验证法CV-SVM虽然有较高的准确率和较好的稳定性，但其所耗费的时间太长；基于遗传算法的支持向量机GA-SVM变压器故障诊断，虽然在运行分类诊断的时间上有所提高，但其运行分类诊断的准确率及稳定性不如传统的交叉验证法CV-SVM；基于粒子群算法的PSO-SVM变压器故障诊断在较基于遗传算法的支持向量机GA-SVM变压器故障诊断在分类诊断准确率及稳定上有了进一步的提高，与传统的交叉验证发CV-SVM差别不大，但所耗费的时间却比基于遗传算法的支持向量机GA-SVM变压器故障诊断在分类诊断的时间多。而本文所提出的基于蜻蜓算法的支持向量机DA-SVM的变压器故障诊断，与上述3种算法相比，所耗费的时间少，寻优能力强，分类器的准确率与变压器故障诊断的准确率都更高，稳定性好，且收敛性好，收敛速度快。

4　总结

针对电力变压器运行状态直接影响到电网的运行安全，正确诊断电力变压器的潜伏性故障对提高电力系统的运行安全性、可靠性及经济性具有重要意义及支持向量机惩罚参数C和核参数g对SVM分类器的性能有重要影响，提出元启发算法基于蜻蜓算法的支持向量机DA-SVM变压器故障诊断。通过4种算法：基于蜻蜓算法的支持向量机DA-SVM的变压器故障诊断法、传统的交叉验证法支持向量机CV-SVM变压器故障诊断法、基于遗传算法的支持向量机GA-SVM变压器故障诊断法及基于粒子群算法的PSO-SVM变压器故障诊断法对变压器油色谱数据进行变压器故障诊断试验，从对比试验中的数据及图形可以得出：本文提出的元启发算法基于蜻蜓算法的支持向量机DA-SVM的变压器故障诊断方法，在对变压器进行故障诊断中，有更好的分类器准确率及故障诊断正确率，且在SVM分类器的参数组合（C，g）寻优中较其他3种算法有耗费时间少，寻优能力强，稳定性好，且收敛性好，收敛速度快的优越性。

［1］赵峰，李硕.基于DGA和改进型灰关联度模型的牵引变压器故障诊断［J］.高电压器，2015，51（1）：41-45.

［2］薛浩然，张珂珩，李斌，等.基于布谷鸟算法和支持向量机的变压器故障诊断［J］.电力系统保护与控制，2015，43（8）：8-13.

［3］田冲.电力变压器状态评估及故障诊断方法研究［D］.重庆：重庆大学，2015.

［4］牛东晓，谷志红，邢棉，等.基于数据挖掘的SVM短期负荷预测方法研究［J］.中国电机工程学报，2006，26（18）：6-12.

［5］尹金良，朱永利，俞国勤，等.基于高斯过程分类器的变压器故障诊断［J］.电工技术学报，2013，28（1）：158-164.

［6］石晓艳，刘淮霞，于水娟.鲶鱼粒子群算法优化支持向量机的短期负荷预测［J］.计算机工程与应用，2013，49（11）：220-227.

［7］郭创新，朱承治，张琳，等.应用多分类多核学习支持向量机的变压器故障诊断方法［J］.中国电机工程学报，2010，30（13）：128-134.

［8］陈小青，刘觉民，黄英伟，等.采用改进人工鱼群优化粗糙集算法的变压器故障诊断［J］.高电压技术，2012，38（6）：1403-1409.

［9］茆美琴，龚文剑，张榴晨，等.基于EEMD-SVM方法的光伏电站短期出力预测［J］.中国电机工程学报，2013（34）：17-24.

［10］尹金良，朱永利.支持向量机参数优化及其在变压器故障诊断中的应用［J］.电测与仪表，2012，49（5）：11-16.

［11］衷路生，齐叶鹏，杨辉，等.PSO优化的LS-SVM在列车弓网系统的建模研究［J］.华东交通大学学报，2012，29（3）：1-6.

［12］傅军栋，邹欢，康水华.PSO-SVM算法在智能建筑环境监控系统中的应用［J］.华东交通大学学报，2016，33（1）：121-127.

［13］PIATT I C.Fast training of support vector machines using sequential minimal optimization［C］//Advances in Kernel Methodssupport Vector Rning，MIT Press，1999：185-208.

［14］BRERETON R G，LLOYD G R.Support vector machines for classification and regression［J］.Analyst，2010，135（2）：230-67.

［15］MIRIALILI S.Dragonfly algorithm：a new meta-heuristic optinization technigue for solving single-objective，discrete，and multiobiective problems［J］.Neural Computing&Applications，2015，27（4）：1-21.

［16］谢龙君，李黎，程勇，等.融合集对分析和关联规则的变压器故障诊断方法［J］.中国电机工程学报，2015（2）：277-286.

［17］费胜巍，苗玉彬，刘成良，等.基于粒子群优化支持向量机的变压器故障诊断［J］.高电压技术，2009，35（3）：509-513.

［18］宋永东.支持向量机参数选择的研究［D］.湖北：华中师范大学，2013.

［19］郑含博，王伟，李晓纲，等.基于多分类最小二乘支持向量机和改进粒子群优化算法的电力变压器故障诊断方法［J］.高电压技术，2014，40（11）：134-139.

（责任编辑刘棉玲）

Transformer Fault Diagnosis Based on Dragonfly Optimization Algorithm and Support Vector Machine

Fu Jundong，Chen Li，Kang Shuihua，Feng Yixuan
（School of Electrical and Electronic Engineering，East China Jiaotong University，Nanchang 330013，China）

Power transformer is an important electrical equipment used to transform voltage，transmit and distribute power，and its running state directly affects the safety of power network.In order to improve the accuracy of fault diagnosis，this paper puts forward a kind of method for transformer fault diagnosis based on Dragonfly Algorithm（DA）and support vector machine（SVM）.Parameters of SVM classifier are optimized by DA and fitness function is implemented according to the maximum accuracy of SVM classification prediction.Transformer fault diagnosis example results show that，DA-SVM based on dragonfly algorithm，compared with cross validation method of transformer fault diagnosis CV-SVM，GA-SVM based on genetic algorithm（GA），and PSO-SVM based on particle swarm algorithm，has high accuracy of fault diagnosis，good global search capability，high convergence speed and superiority with good stability.

dragonfly algorithm（DA）；support vector machine（SVM）；transformer；fault diagnosis

TM715

A

1005-0523（2016）04-0103-10

2016－03－04

傅军栋（1972—），男，副教授，研究方向为电力系统、智能化建筑。