基于PANDA软件的框架网坐标解算可靠性分析

马飞虎，饶志强，李　胜，姜珊珊

（1.华东交通大学土木建筑学院，江西 南昌330013；2.新疆维吾尔自治区测绘科学研究院，新疆 乌鲁木齐830002）

基于PANDA软件的框架网坐标解算可靠性分析

马飞虎1，饶志强1，李胜2，姜珊珊1

（1.华东交通大学土木建筑学院，江西 南昌330013；2.新疆维吾尔自治区测绘科学研究院，新疆 乌鲁木齐830002）

应用高精度定位解算软件PANDA对框架网进行解算，并与Bernese解进行比较，探讨不同软件模型下框架网的点位坐标解算方法及其精度；通过算例表明PANDA软件的定位解算结果与Bernese的解有较好的一致性，表明PANDA软件有较高的可靠性和稳定性。

框架网坐标；精度比较分析；Bernese；PANDA

目前，国内外开发出了很多的高精度定位解算软件，其中具有代表性的有瑞士伯尔尼大学天文研究所研制的Bernese软件［1］，美国喷气动力实验室（JPL）研制的GIPSY软件和我国武汉大学卫星导航定位技术研究中心研制的PANDA软件［2］。Bernese软件既能用非差方法进行单点定位，又可用双差方法进行整网平差，而且它能同时将多GPS数据和GLON-ASS数据进行处理。而PANDA软件基于非差处理模式，能实现对GNSS/SLR/DORIS/VLBI等多类观测数据的后处理与实时处理分析，目前主要应用于导航卫星精密定轨与时间同步，对地观测卫星精密定轨和大网数据处理与高精度PPT定位［3-4］等领域，且可用于实时和动态定位中。

本文以Bernese软件为参照，比较分析了PANDA和Bernese软件解算精度及可靠性，以框架网为基础，进行定位解算，通过对框架网的点位坐标及其精度指标进行分析。结果表明PANDA和Bernese软件解算结果具有较高的一致性，间接说明了PANDA软件坐标解算的可靠性及稳定性。

1　Bernese软件定位解算流程

Bernese软件是由Bernese University和Astronomical Institute研究开发的GPS数据 （包括GLONASS数据、GPS和GLONASS混合数据）处理软件，该软件界面友好，模块条理清晰，并且内嵌有图形软件，功能强大，它用双差相位观测进行高精度的测地应用，可以实现精密定轨，有Ll和L2不同的线性组合，可以利用非差观测进行钟差估计，并实现多种类型参数的估计。其精度高，数据处理模型严密，使得它很适合长基线GPS网的数据处理。

1.1软件解算策略

1.1.1数据预处理

Bernese采用M-W组合和LG组合进行周跳探测与粗差剔除［5-6］，以卫星弧段为单位，首先计算一弧段M-W组合宽巷模糊度NΔ的时间序列及其中误差σ，如果σ超出指定阈值，则认为此弧段可能有周跳，需进行周跳探测。探测的结果要使得该弧段中误差满足指定阈值。利用LG组合对M-W组合探测到的周跳进行检测并确定周跳大小。选择周跳发生历元的前后各10个历元（默认值）的LG组合观测值，分别进行线性拟合，两拟合多项式的中误差及其在周跳发生历元的差值的小数部分均满足指定的阈值，则此历元发生周跳并计算L1、L2上周跳的大小［7］。

1.1.2参数估计

Berense使用最小二乘参数估计法对非差精密单点定位中的参数进行估计，采用参数消除法对多余参数（坐标参数、钟差参数、对流层参数、电离层参数［8］和模糊度等参数）进行等价消除［5，9］，以减少法方程维数，提高计算的速度及效率。对于被消除的参数，其信息并未被消除，仍保留在法方程中，可通过参数恢复进行求解［10］。

1.2数据处理流程

数据处理分为4大步：数据的准备，标准轨道的生成，数据预处理，参数估计。

1）数据准备：包括观测数据和星历数据的准备；

2）生成标准轨道：通过星历文件来生成标准轨道，以备下一步使用；

3）数据的预处理：主要完成对观测数据的预处理工作，进行周跳探测、剔除质量差的数据并形成单差文件等；

4）参数估计：实现对大气层延迟的参数估计、点位坐标（X，Y，Z）的估计等。

本文使用双差计算所获得数据，因此下述就以GPS数据双差处理模式精确求解点位坐标［11］来说明Bernese软件的数据处理方法。Bernese软件的数据处理方法，即定位解算流程如图1所示。

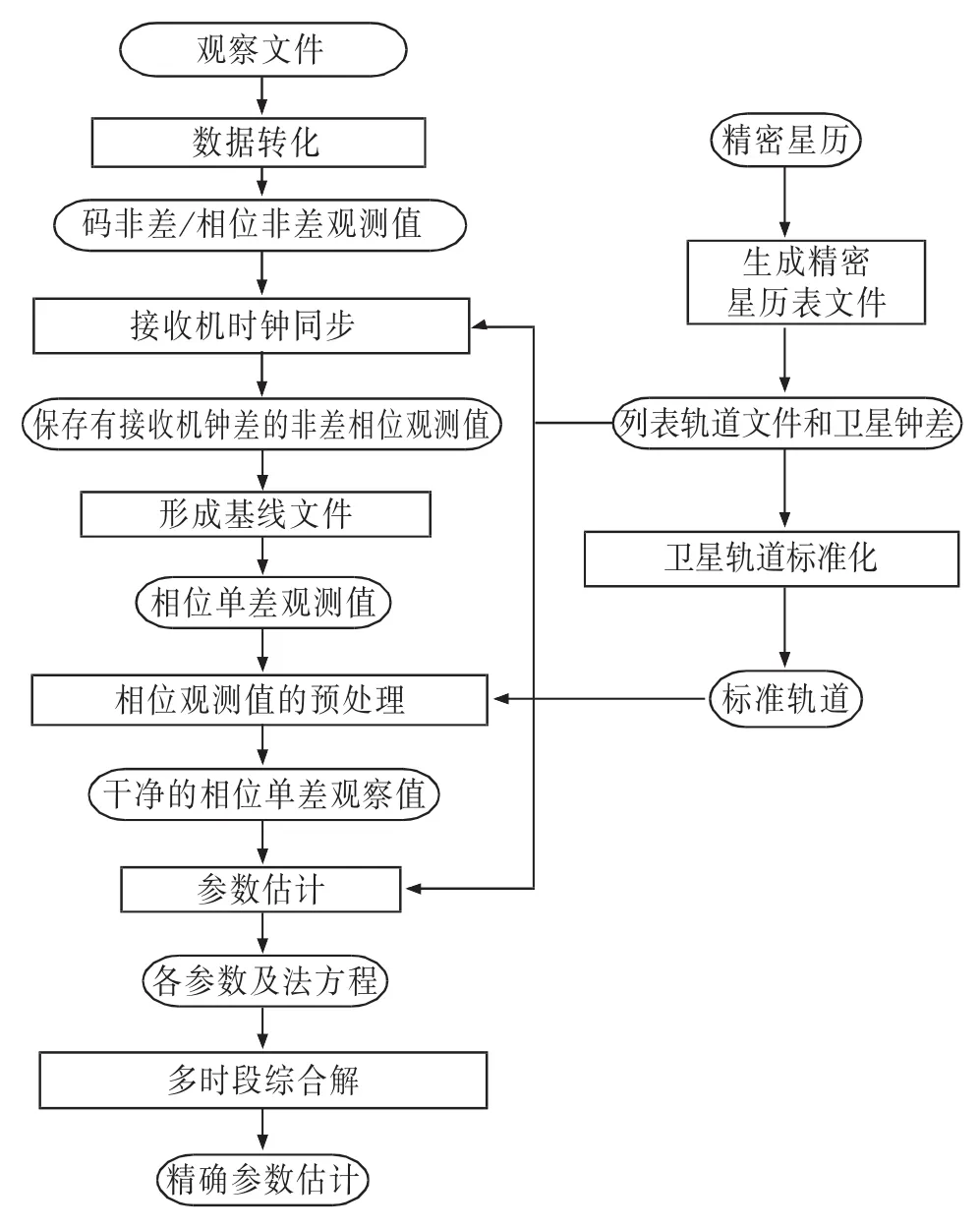
图1　Bernese软件定位解算流程示意图Fig.1　Bernese software positioning solution process diagram

2　PANDA软件数据处理策略

2.1精密静态定位数学模型

精密静态单点定位中使用的是载波相位观测值，观测方程为［12-13］

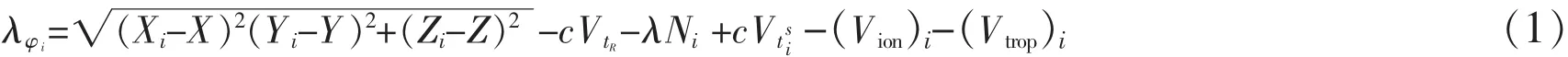
式中：（Xi，Yi，Zi）为根据卫星星历求得的卫星在空间的位置；（X，Z）为接收机观测瞬间卫星在空间的位置；VtR为接收机的钟差改正；Vt为第i颗卫星的卫星钟差改正；（Vion）i为第i颗卫星在传播路径上的电离层延迟改正；（Vtrop）i为第i颗卫星在传播路径上的对流层延迟改正。经过线性化之后的观测方程为［14］

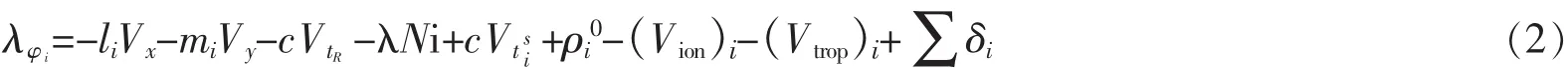
si，为从测站的近似位置至第i颗卫星间的距离；φi为卫星i的载波相位观测值，由整周计数Int（φ）i和不足一周的部分Fr（φ）i组成；λ为载波的波长；Ni为与φi相应的整周模糊度；为定位计算时必须考虑到的各种改正数，如天线相位中心偏差改正、引力延迟改正、海潮负荷改正、地球固体潮改正等；其余符号的含义同式（1）。由于根据导航电文得出的卫星钟差精度过低，故在精密单点定位中其不能作为已知值采用，必须另行设法解决。电离层延迟（Vion）i可通过双频观测来予以消除，接收机钟差改正VtR

可通过在卫星间求单差来予以消除，采用非差观测值时需作为未知参数来加以估计。在数据处理过程中需用到接收机钟差的近似值则由测码伪距单点定位来提供［15］。

2.2数据处理策略

PANDA软件在进行定位解算时加入了武汉大学建立的覆盖亚太及欧非地区的北斗/GPS观测网络数据和武汉大学提供的北斗精密星历。

PANDA软件采用非差处理模式，软件从读取GPS标准数据格式RINEX开始，软件的数据编辑模块采取与Blewitt一致的单站数据自动处理方法，尽可能地发现和修复周跳，并剔除异常观测值，输出干净数据，进入参数估计模块。参数估计模块采用均方根信息滤波与最小二乘两个并置的估计器，均方根信息滤波包括前向均方根信息滤波器（SRIF）和后向均方根信息平滑器（SRIS），在利用非差观测值定轨时的参数估计过程中，SRIF能有效克服滤波器的发散，具有较高的数值稳健性和计算高效性［16-17］。最小二乘估计器主要应用于事后处理，这有利于节省计算时间和基于观测值残差的数据再编辑。软件考虑尽可能多的改正项，未能精确模型化的误差因素通过参数估计吸收。同时为了灵活应用于实时和动态定位［18］，软件采用逐个历元地建立观测方程的方法［19］。PANDA软件采用的观测值模型、摄动力模型以及数据处理流程详细内容可参见文献［20］。图2为PANDA软件数据处理的策略。

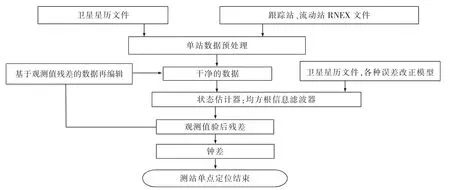
图2　PANDA数据处理策略Fig.2　PANDA data processing strategy

3　算例及精度分析

对在新疆地区建立的6个GNSS基准站（站点分布图如图3所示）进行了连续观测，采用了观测日期为2014年2月1日—2014年2月7日，共7天数据，解算时加入2个IGS站（乌鲁木齐和拉萨）作为基准站。用Bernese和PANDA软件对GPS数据进行处理时，所采用的参数（见表1）是一致的。2种软件的具体解算策略如上2、3节所述。Bernese和PANDA软件解算坐标的精度在X、Y、Z方向的比较结果如图4所示。

图4（a）表明在X方向上PANDA解算精度最大值为白杨沟站7 mm，Bernese解算精度最大值同样也是白杨沟站5 mm，但是解算精度最好的站点PANDA软件为昌吉站2 mm，Bernese软件解算精度最好的站点为红山站。2种软件在X方向上解算精度相差最大的为3 mm。图4（b）表明在Y方向上PANDA解算精度最大值为昌吉站19 mm，Bernese解算精度最大值是白杨沟站19 mm，解算精度最好的站点PANDA软件为红山站13 mm，Bernese软件解算精度最好的站点同样也为红山站11 mm。2种软件在X方向上解算精度相差最大的为4mm。图4（c）表明在Z方向上PANDA解算精度最大值为天池站17 mm，Bernese解算精度最大值是白杨沟站17 mm，解算精度最好的站点PANDA软件为昌吉站10 mm，Bernese软件解算精度最好的站点同样也为红山站8 mm。2种软件在X方向上解算精度相差最大的为3 mm。结果表明，两者的精密单点定位精度在X，Y，Z方向只存在mm级差异，说明了两者解算结果有较好的一致性。而用2种软件对GPS数据进行整网解算时，测站的解算精度Y，Z方向都在2 cm以内，在X方向上精度较好都在1 cm以内。

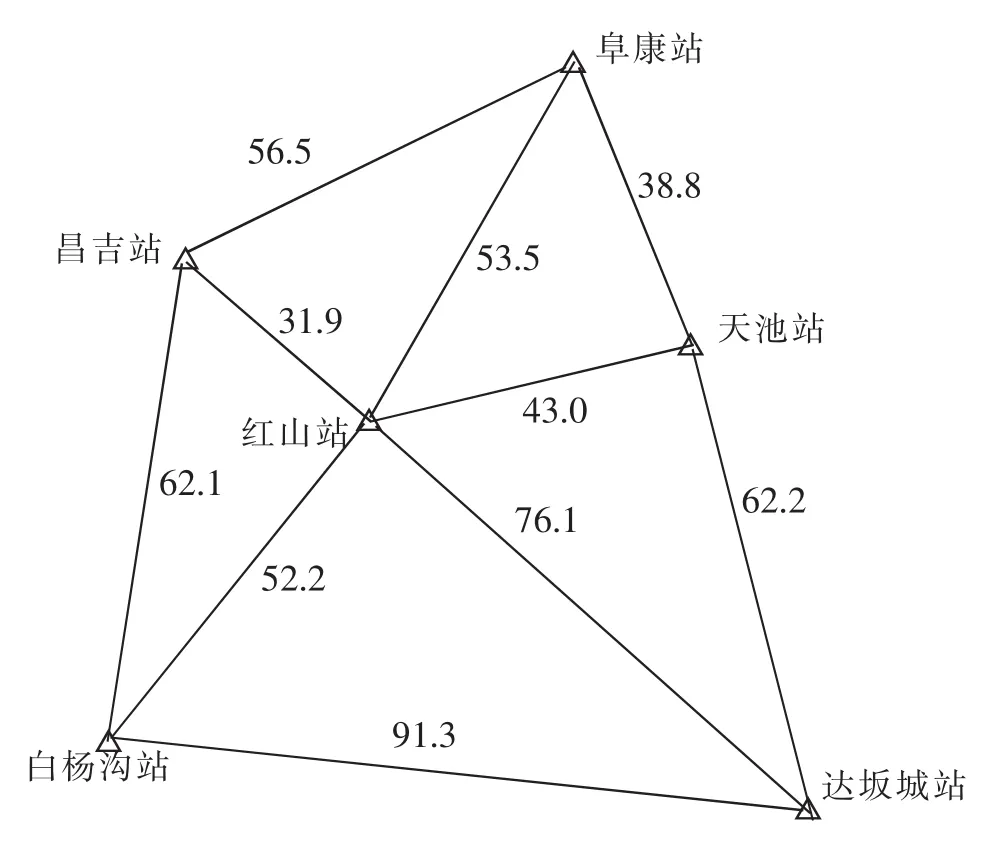
图3　站点分布图（单位：km）Fig.3　Site distribution map

4　结论

通过本文的分析可知，采用IGS提供的精密星历和精密钟差产品，利用Bernese和PANDA软件进行单点定位解算，虽然两者所采用的算法和策略存在不同，但结果表明两者解算结果有很好的一致性，说明了PANDA软件具有很高的稳定性和可靠性，其已经具备了实时精密单点定位的能力，有着广泛的应用价值（如高精度动态导航、低轨卫星的定轨等）。

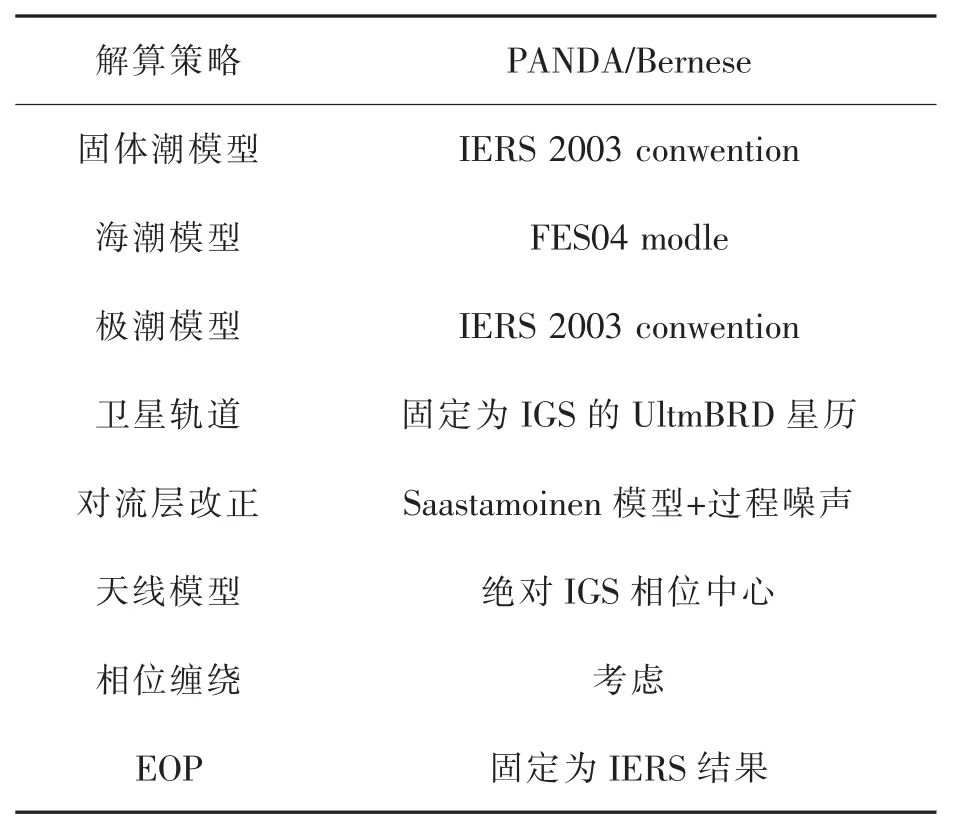
表1　PANDA与Bernese处理策略Tab.1　Processing strategies of PANDA and Bernese

图4　Bernese和PANDA软件解算坐标的精度在X，Y，Z方向的比较结果Fig.4　Comparison results of the coordinate accuracy calculation by Bernese and PANDA in X，Y，Z direction

［1］HUGENTOBLER U，SCHAER S，FRIDEZ P.Bernese GPS software Version 4.2［CP］.Astronomical Institute，University of Bern，2001.

［2］施闯，赵齐乐，李敏，等.北斗卫星导航系统的精密定轨与定位研究［J］.中国科学：地球科学，2012，42（6）：854-861.

［3］姜卫平，邹璇，唐卫明.基于CORS网络的单频GPS实时精密单点定位新方法［J］.地球物理学报，2012，55（5）：1549-1556.

［4］张小红，左翔，李盼，等.BDS/GPS精密单点定位收敛时间与定位精度的比较［J］.测绘学报，2015，44（3）：250-256.

［5］DACH R，HUGENTOLBER U，FRIDEZ P，et al.Bernese GPS Software Version 5.0［CP］.Astronomical Institute，University of Bern，2007.

［6］TEFERL F N，ORLIAC E J，BINGLEY R M.An assessment of Bernese GPS software precise point positioning using IGS final products for global site velocities［J］.GPS solutions，2007，11（3）：205-213.

［7］谭争光，郭金运，宗干，等.PANDA和Bernese软件的PPP比较分析［J］.全球定位系统，2013，38（5）：60-64.

［8］许艳，杨元喜，许国昌，等.南极GPS定位中的电离层延迟分析［J］.北京航空航天大学学报，2013，39（10）：1370-1375.

［9］GE M，GENDT G，DICK G，et al.A new data processing strategy for huge GNSS global networks［J］.Journal of Geodesy，2006，80 （4）：199-203.

［10］方荣新，施闯.高采样率GPS数据非差精密处理方法及其在地震学中的应用研究［D］.武汉：武汉大学，2010.

［11］胡辉，方玲，雷明东，等.GPS接收机C/A码跟踪算法及环路控制策略［J］.华东交通大学学报，2013，30（1）：64-70.

［12］徐爱功，赵亮，周阳.基于PANDA软件的GPS静态精密单点定位精度分析［J］.测绘通报，2013（10）：5-7.

［13］赵鑫，秦红磊，郎荣玲.基于优化理论的GPS定位解算算法［J］.北京航空航天大学学报，2012，38（9）：1219-1223.

［14］袁丰波.半参数模型在GPS高程拟合和单点定位中的应用［D］.桂林：桂林理工大学，2012.

［15］刘精攀.GPS非差相位精密单点定位方法与实现［D］.河海大学，2007.

［16］BIERMAN G J.Factorization methods for discrete sequential estimation［M］.New York：Academic Press，1972：27-1972.

［17］赵齐乐，刘经南，葛茂荣，等.用PANDA对GPS和CHAMP卫星精密定轨［J］.大地测量与地球动力学，2005，25（2）：113-117.

［18］陈克杰，方荣新，李敏，等.PANDA软件在高频数据PPP动态定位中的应用研究［J］.大地测量与地球动力学，2011，31（4）：132-135.

［19］耿涛，赵齐乐，刘经南，等.基于PANDA软件的实时精密单点定位研究［J］.武汉大学学报：信息科学版，2007，32（4）：312-315.

［20］赵齐乐.GPS导航星座及低轨卫星的精密定轨理论和软件研究［D］.武汉：武汉大学，2004.

（责任编辑姜红贵）

Reliability Analysis of Framework Coordinate Solution Based on PANDA Software

Ma Feihu1，Rao Zhiqiang1，Li Sheng2，Jiang Shanshan1
（1.School of Civil Engineering and Architecture，East China Jiaotong University，Nanchang 330013，China；2.Xinjiang Academy of Surveying&Mapping，Urumqi 830002，Xinjiang）

This paper discusses GPS framework data processing with high-precision data post-processing software PANDA，and then compares with the solution of Bernese.It explores the strategy of point coordinate solution and related accuracy evaluation.The examples show that there is a good consistency between Bernese and PANDA solution，which indicates PANDA software has high reliability and stability.

GPS framework；accuracy analysis；Bernese；PANDA

P228

A

1005-0523（2016）04-0098-05

2016－03－09

测绘地理信息行业科研专项（201512027，201512021）；江西省数字国土重点实验室开放研究基金资助项目（DLLJ201605）

马飞虎（1973—），男，副教授，博士，研究方向为3S技术集成、工程测量、智能交通等。