双曲线型薄壁堰泄流规律的数值模拟

魏文礼，张泽伟， 白朝伟， 刘玉玲

(西安理工大学 陕西省西北旱区生态水利工程重点实验室，陕西 西安 710048)



双曲线型薄壁堰泄流规律的数值模拟

魏文礼，张泽伟， 白朝伟， 刘玉玲

(西安理工大学 陕西省西北旱区生态水利工程重点实验室，陕西 西安 710048)

【目的】 推求双曲线型薄壁堰堰流的基本方程式，确定双曲线型薄壁堰的流量系数，为实际工程中流量的控制和测量提供参考。【方法】 根据双曲线构建了双曲线型薄壁堰，通过能量方程式推导其流量的计算公式；数值模拟了4种不同堰顶水头的过流能力，根据模拟的流量数据利用最小二乘法拟合流量与堰顶水头的关系式，与理论推求的堰流基本公式相结合确定双曲线型薄壁堰的流量系数，辅以RNGk-ε湍流模型数值求解气液两相流时均方程；使用半隐式SIMPLE(Semi-implicit method for pressure-linked equations)算法求解速度与压力耦合方程组，并用VOF(Volume of fluid)法模拟自由水面。【结果】 理论公式计算的流量与数值模拟的流量相差甚微，相对误差在 0.3% 以内，证明本研究推求公式正确。【结论】 双曲线型薄壁堰的流量与堰顶水头成正比关系，该关系为流量的控制和测量提供了便利。

双曲线型薄壁堰；流量系数；数值模拟；流量公式

在渠道、水槽中常用溢流堰来量测水流流量，常见的溢流堰有薄壁堰、宽顶堰、实用断面堰等，其中最常用的是薄壁堰。薄壁堰流具有稳定的水头与流量关系，是一种使用最早而且精度较高的测流设施，具有制造简单、装设容易、造价较低等优点，广泛用于水力学、水工实验室及灌排渠道上。经过多年的实践，学者们已经由试验得出大量流量计算的经验公式[1]。

虽然对不同堰型经验公式的研究已较为成熟，但考虑到不同堰型的经验公式种类繁多、不易挑选且各自求得的流量存在差异等问题，在某一流量区间内选取准确的堰型并采用精确度高的经验公式就显得尤为重要。Aydin等[2]在实际渠道和实验室分别对矩形堰流量进行了研究，认为堰的高度、宽度及堰顶水头与其流量有一定关系，实验室试验是通过测量流量与堰顶水头、堰的高度以及宽度的变化进行的，试验表明流量独立于堰的高度，当堰的宽度一定时其与堰顶水头有一定关系。周华兴等[3]为了规范量水堰的设计与应用，对设计与应用中的量水堰流量计算公式、小流量时的表面张力以及堰后通气孔等问题进行了探讨。不同堰流形态是坝体溢流和闸坝溢流常见的一种水流现象。杜伟等[4]介绍了堰流的概念、水流形态类型、流量计算的基本公式和单宽流量的图解法与查表法。刘韩生[5]对三角剖面堰流量公式及流量系数进行了详细的研究分析。邓洪福等[6]以标定的三角形薄壁堰作为测流控制条件，对矩形薄壁堰、WES实用堰、圆角宽顶堰和直角宽顶堰进行了测流试验，分别采用相应的堰流公式进行了计算和比较，表明不同堰型堰流公式计算值各有差异，同一堰型采用不同经验公式求得的流量亦有所差别，对不同经验公式得出的流量和标准流量进行了比较及偏离程度分析，初步得出不同堰型流量计算的推荐公式。刘焕芳等[7]针对标准梯形量水堰在灌区量水中存在的问题，提出改进标准梯形量水堰及其测流公式，并对其进行了试验研究，得出了改进后梯形量水堰的测流公式，同时还进行了该量水堰的测流精度分析和原型观测试验。曾甄等[8]和彭新民等[9]分别对迷宫堰的流量系数和水力特性进行了研究，给出了迷宫堰流量系数的计算公式，为迷宫堰的设计工作提供了方便。商艾华等[10]研究了复合堰的水力特性，推导了复合堰的流量公式，而后通过在不同流量下对不同测流断面进行分析和对比，给出了这种堰型自由流流量系数公式，在理论上予以阐述和论证，最后提出了由实测水头直接计算流量的流速系数法。

随着计算流体力学(CFD)方法的发展与应用，许多学者将溢流堰的计算与数值模拟结合起来分析研究溢流堰的过流能力。陈大宏等[11]利用三维紊流模型封闭雷诺时均方程，VOF方法追踪自由表面，对过堰流动进行了数值模拟。李玲等[12]介绍了VOF模型及其应用方法，结合 紊流模型和分段线性方式构造界面的方法，数值求解了带自由水面的三维水流流动问题，并以大型水工建筑物溢洪道内水流流动为例，计算了溢洪道内水流的流动特性，所得计算值与实测值相吻合，说明VOF模型能够精确地跟踪自由表面，适用于溢洪道等大型水工建筑物内水流流动的数值模拟。也有将数值模拟方法应用于其他模型的情况[13-16]，结果都证明了数值模拟的可行性。

虽然目前对多种溢流堰的测流规律已有研究，但其流量的计算公式都较为复杂，没有一种堰型的水头与流量成简单的正比关系，况且尚未发现有关双曲线型薄壁堰堰流公式的理论推导研究。为此，本研究通过能量方程式推求了堰顶水头与流量成正比关系的双曲线(y=a2x-2)型薄壁堰的堰流基本方程式，并与数值计算方法相结合确定双曲线型薄壁堰的流量系数，以期为将其方便应用于各种情况下的流量控制和测量提供参考。

1　双曲线型薄壁堰堰流公式的推导

为了得到双曲线型薄壁堰的流量公式，特做以下假设，这些假设带来的误差可以通过流量系数来消除。假设：

1)堰上水流是垂直于堰顶线水平投影的单向水流；

2)沿同个堰型堰宽的流量系数都相同，为一常数；

3)上游堰面延长与水面交线处的过流断面的水流为渐变流；

4)曲线方程意味着当y趋近于0时，x趋近于无穷大。在实际应用中，由于不可能将曲线堰的孔口底部做成无穷大，所以通常在孔口底部加上一个小的矩形作为补偿，这样就形成了完整的曲线堰孔口轮廓，如图1所示。在理论推导其堰流流量公式时将其作为完整的理想曲线堰来处理。

堰口双曲线公式为y=a2x-2，(当曲线确定时，a为一常数)，做相应的变化得x=(a2/y)1/2，则有：

(1)

根据能量方程[17]，得

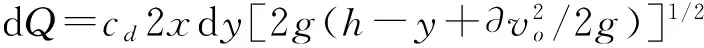
(2)

式中：Q为过堰流量；cd为堰的流量系数；g为重力加速度；h为堰顶水头；∂为动能修正系数；v0为过水断面的平均流速，即行进流速。

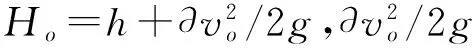
dQ=cd2(a2/y)1/2[2g(Ho-y)]1/2dy。

(3)

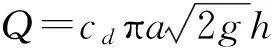
(4)

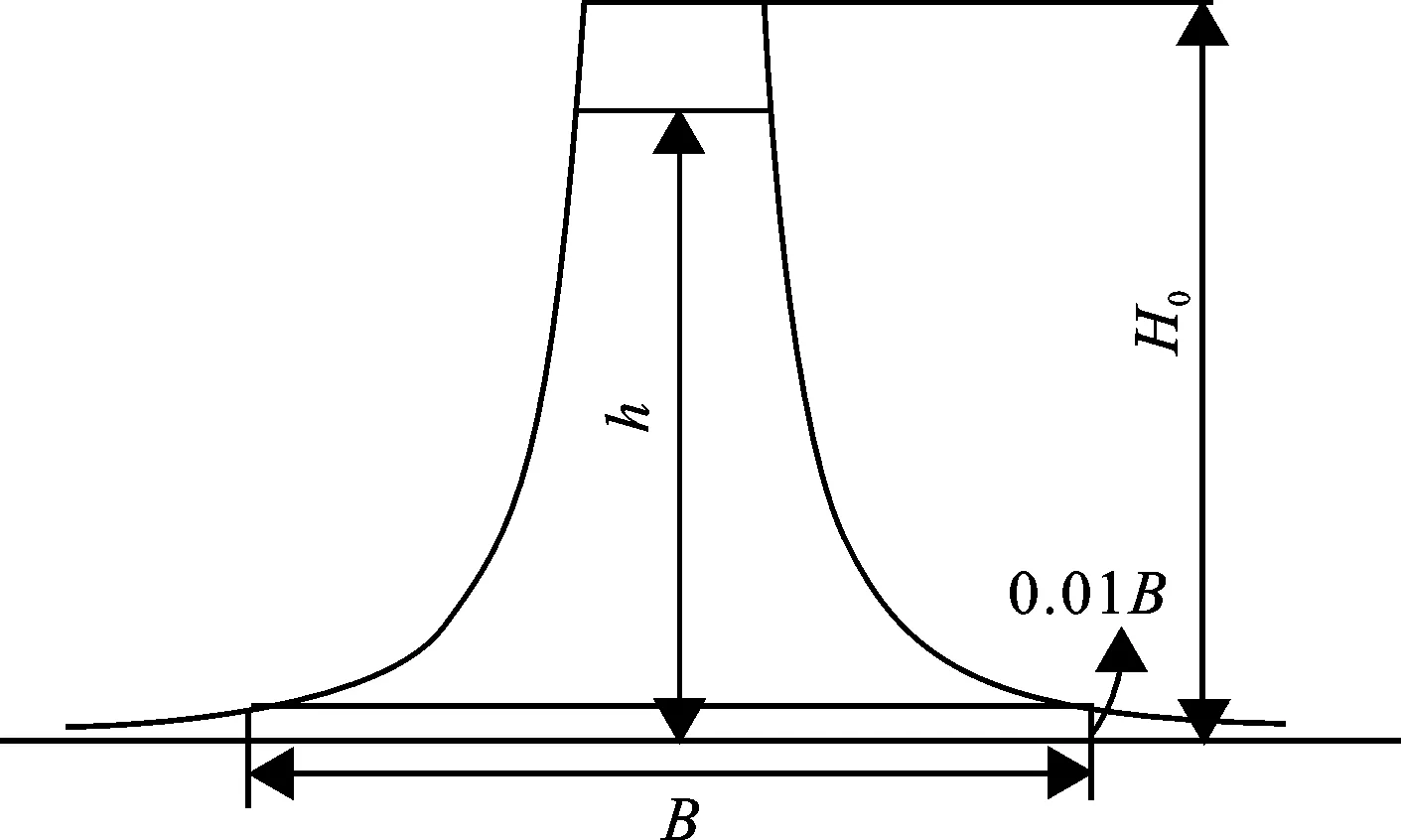
图 1　双曲线型薄壁堰堰口的实际形状Fig.1　Actual shape of the weir

2　计算模型的建立

2.1湍流模型的选择

RNGk-ε紊流模型较标准k-ε模型能更好地模拟流线弯曲程度较大的流动，故这里选择 RNGk-ε紊流模型进行建模，其控制方程如下[18-19]。

连续方程：

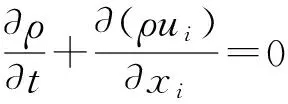
(5)

式中：ρ为流体密度，t为时间，ui为沿i(i为笛氏坐标x、y或z)方向的时均速度分量，xi为沿i方向的空间坐标分量。

雷诺方程：

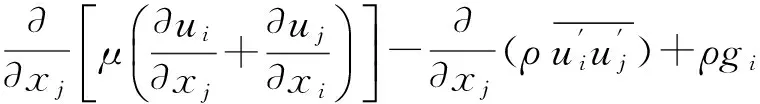
(6)

(7)

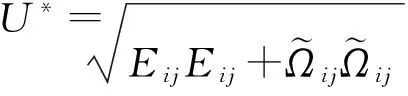
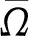
δij为Kronecker函数，δij=1(i=j),δij=0(i≠j)。

湍动动能k方程：

(8)

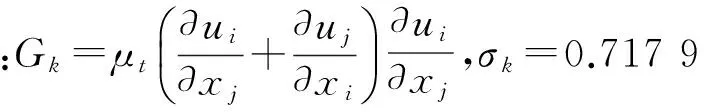
湍动动能耗散率ε方程：

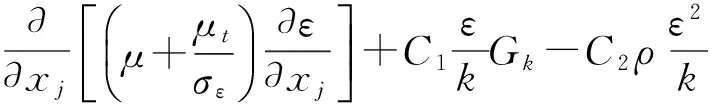
(9)

式中:

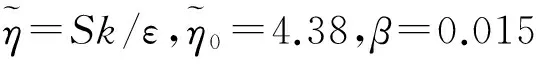
C2=1.68

以上方程组构成了求解流场分布规律的封闭方程组，根据实际工况施加相应的边界条件后，构成该方程组的定解问题。

2.2模拟自由水面的VOF法

VOF方法的基本原理[20]是通过研究网格单元中流体和网格体积比函数Fw(xi,t)(i=1,2,3)来确定自由面，追踪流体的变化而非追踪自由液面上质点的运动，若Fw(xi,t)=1，则表示该单元被液体充满；当Fw(xi,t)=0，则表示其是一个空单元；若Fw(xi,t)∈(0,1)，则表示该单元部分充满液体。

描述Fw的控制方程为：

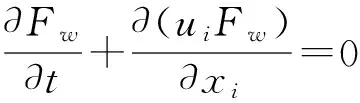
(10)

引入VOF后，ρ、μ是Fw(xi,t)的函数，其表达式为：

ρ=Fwρw+(1-Fw)ρa。

(11)

μ=Fwμw+(1-Fw)μa。

(12)

式中：ρw和ρa分别为水和空气的密度，μw和μa分别为水和空气的分子黏性系数。

将上述方程(10)、(11)和(12)与紊流数学模型基本方程(5)-(9)联立求解, 就可得到相应各未知变量,如压力、流速、紊动动能、紊动耗散率以及水体体积率函数等的分布。

3　计算区域

选取长6 m、宽1 m、高1.25 m的矩形明渠为研究对象，在长为3 m的地方设置量水堰，挡板高为0.3 m、厚4 mm，堰后为自由跌落的水渠，底板比堰前低0.5 m。本研究使用的曲线堰为双曲线堰y=a2x-2，a=0.05。分别设计进口水位为0.4， 0.5，0.6和0.7 m的4种工况。模型示意图如图2所示。

4　网格划分与边界条件及求解方法

初始计算网格由GAMBIT软件生成，网格划分采用了结构化网格，如图3所示，网格总单元数为56 232个。

模拟气液两相流时采用VOF方法，主要是捕捉气液交界面。进口定义为压力进口边界，分别计算了4种进口水头情况；出口边界条件设定压力出口边界，出口处设置水深为 0.3 m；顶面与大气相通，定义相对压强为0；明渠固体壁面(包括挡板)上的边界条件按“壁面函数”法给定。

采用非稳定流模型，控制方程的离散采用有限体积法，速度与压力耦合方程组求解时使用半隐式SIMPLE(Semi-implicit method for pressure-linked equations)算法。

5　数值模拟结果与流量系数的确定

计算以进出口流量的差值作为判断计算是否收敛的依据，当进出口流量差值小于5‰时，认为计算收敛。堰顶水头为0.3 m时，不同时刻模拟的水面如图4所示。由图4可以看出，此工况不同时刻水舌与水面的变化过程。

将堰顶水头与数值模拟所得流量列于表1，并做成散点图，结果如图5所示。从图5可以看出，堰顶水头与数值模拟的流量近似在一条直线上。

表 1　不同进口水位下堰顶水头与模拟流量的关系Table 1　Relationship between head crest and simulated discharge with different inlet water levels

图 5　数值模拟流量与堰顶水头的关系Fig.5　Relationship of simulated discharge and water head

将理论公式(4)计算的流量与数值模拟的流量及相对误差列于表2。由表2可以发现，数值模拟的流量与理论公式(4)计算的流量相差甚小，其相对误差最大为0.281%，最小为0.103%，相对误差的平均值为0.199%。产生误差主要原因是在理论推导公式时采用完整的曲线，忽略了下面小长方形区域两边无限延伸的小区域；另外，推导的公式中将堰前总水头近似用堰顶水头所代替，因此导致理论公式计算值与数值模拟值出现了一定的误差。

为了验证本研究推求的流量系数的可靠性，现在分别给出3个堰顶水头，将数值模拟与理论公式(4)得到的流量值进行比较分析，结果见表3。由表3可以看出两者的流量值比较接近，相对误差最大为0.246%，最小为0.081%，相对误差均较小，这在一定程度上验证了本研究推求公式的合理性。

表 2　数值模拟流量与理论公式计算流量的比较Table 2　Comparison of simulated and theoretical discharges

表 3　双曲线型薄壁堰流量系数的验证Table 3　Verification of flow coefficient of the hyperbolic thin-walled weir

6　结　论

本研究应用能量方程式推求了双曲线型薄壁堰流量的基本计算公式，表明流量与堰顶水头成正比关系，因此称其为比例堰。基于其泄流流量和堰顶水头呈正比例函数的特点，使得比例堰能够方便地应用于各种情况下流量的测量和控制。

采用数值模拟的方法，通过数值模拟双曲线型薄壁堰的过流能力，得到不同堰顶水头下的流量值，利用最小二乘法拟合确定堰顶水头与流量之间的函数关系，得到一个确定的流量关系式，将其与推导的堰流流量基本公式对比，确定了此堰的流量系数。

数值求解气液两相流模型，结合VOF法能够模拟泄流流场的各种水力参数。因此，数值模拟是一种行之有效的研究方法。

[1]李炜.水力计算手册 [M].北京:中国水利水电出版社，2006.

Li W.Hydraulic calculation manual [M].Beijing:China Water Conservancy and Hydropower Press，2006.

[2]Aydin I,Altan-Sakarya A B,Sisman C.Discharge formula for rectangular sharp-crested weirs [J].Flow Measurement and Instrumentation,2011,22(2):144-151.

[3]周华兴，郑宝友，迟杰，等.规范《薄壁矩形量水堰》的设计与应用 [J].水道港口，2003,24(1):26-30.

Zhou H X,Zheng B Y,Chi J,et al.Design and application of standard “Sharp Edged Rectangular Weir” [J].Journal of Waterway and Harbour,2003,24(1):26-30.

[4]杜伟,朱国锋.堰流的基本型式与基本计算公式 [J].黑龙江水利科技，2012,40(1):171-172.

Du W,Zhu G F.The basic types of weir and the basic formula [J].Heilongjiang Science and Technology of Water Conservancy,2012,40(1):171-172.

[5]刘韩生．三角剖面堰流量公式及流量系数 [J].西北水资源与水工程，1990,1(1)：81-83.

Liu H S.Triangular profile weir flow formula and flow coefficient [J].Water Resources & Water Engineering,1990,1(1)：81-83.

[6]邓洪福，惠源.不同堰型流量计算公式的初步分析 [J].重庆工商大学学报(自然科学版),2011,28(6):644-648.

Deng H F,Hui Y.Analysis of calculation formula for flow rate of different kinds of weirs [J].Journal of Chongqing Technology and Business University(Natural Science Edition),2011,28(6):644-648.

[7]刘焕芳，宗全利，李强，等.灌区梯形量水堰测流改进研究 [J].农业工程学报,2005,21(1):57-60.

Liu H F,Zong Q L,Li Q,et al.Flow measurement improvement of cipoletti weir in irrigation areas [J].Transactions of the CSAE,2005,21(1):57-60.

[8]曾甄，张志军.迷宫堰流量系数的探讨 [J].中国农村水利水电,2005(4):49-52.

Zeng Z,Zhang Z J.Discussion on the discharge coefficient of labyrinth weir [J].Chinese Rural Water and Hydropower,2005(4):49-52.

[9]彭新民,崔广涛，贾树宝.迷宫堰泄流能力及水力特性的试验研究 [J].天津大学学报,2003,36(6):727-730.

Peng X M,Cui G T,Jia S B.Study on discharge capacity of labyrinth weir [J].Journal of Tianjin University,2003,36(6):727-730.

[10]商艾华,郭维东,孟繁星,等.复合堰流量计算 [J].人民长江,2007，38(4):136-146.

Shang A H,Guo W D,Meng F X,et al.Composite weir flow calculation [J].Yangtze River,2007，38(4):136-146.

[11]陈大宏，陈娓.溢流堰水流的三维模拟 [J].武汉大学学报(工学版),2005,38(5):54-56.

Chen D H,Chen W.Three-dimensional simulation of the overflow weir flow [J].Journal of Wuhan University(Engineering Science)，2005，38(5):54-56.

[12]李玲，陈永灿，李永红.三维VOF模型及其在溢洪道水流计算中的应用 [J].水力发电学报，2007,26(2):83-87.

Li L,Chen Y C,Li Y H.Three-dimensional VOF model and it applied in spillway flow calculation [J].Journal of Hydroelectric Engineering，2007,26(2):83-87.

[13]Lü X,Zou Q,Reeve D. Numerical simulation of overflow at vertical weirs using a hybrid level set/VOF method [J].Advances in Water Resources,2011,34(10):1320-1334.

[14]Domnik B,Pudasaini S P,Katzenbach R,et al.Coupling of full two-dimensional and depth-averaged models for granular flows [J].Journal of Non-Newtonian Fluid Mechanics,2013,201:56-68.

[15]Mahmodinia S,Javan M,Eghbalzadeh A.The effects of the upstream Froude number on the free surface flow over the side weirs [J].Procedia Engineering,2012,28:644-647.

[16]Aydin M C.CFD simulation of free-surface flow over triangular labyrinth side weir [J].Advances in Engineering Software,2012,45(1):159-166.

[17]吴持恭.水力学 [M].北京：高等教育出版社,2007:292-295

Wu C G.Hydraulics [M].Beijing:Higher Education Press,2007:292-295.

[18]吴莹莹.氧化沟流场和溶解氧CFD模拟研究:以平顶山污水处理厂为例 [D].武汉:华中科技大学,2009.

Wu Y Y.Simulation on flow field and dissolved oxygen of oxidation ditch:in case of pingding shan waste water treatment plant [D].Wuhan:Huazhong University of Science and Technology,2009.

[19]张土乔，尹则高，毛根海.弯曲圆形管道紊流的数值模拟 [J].水力发电学报，2005,24(3):61-65.

Zhang T Q,Yin Z G,Mao G H.Numerical simulation of turbulence in curved circular duct [J].Journal of Hydroelectric Engineering,2005,24(3):61-65.

[20]Shen Y M，Ng C O，Zheng Y H.Simulation of wave propagation over a submerged bar using the VOF method with a two-equation turbulence modeling [J].Ocean Engineering,2004,31:87-95.

Numerical simulation of discharge of a hyperbolic weir

WEI Wenli,ZHANG Zewei,BAI Zhaowei,LIU Yuling

(StateKeyLaboratoryofEco-HydraulicEngineeringinShaanxi,Xi’anUniversityofTechnology,Xi’an,Shaanxi710048,China)

【Objective】 A theoretical formula for calculating the discharge rate of a hyperbolic thin-walled weir was derived and its flow coefficient was determined to provide reference for controlling and measuring the flow rate in actual project.【Method】 Based on the hyperbolic curve,a hyperbolic weir was constructed and the formula was derived by energy equation.The flow capacity under four different water heads over the crest was simulated.According to the simulated discharge rates,the relationship between discharge rate and corresponding water head over crest was obtained using the least square method.By comparing with the theoretical formula for discharge rate,the flow capacity coefficient of the hyperbolic weir was determined.The gas-liquid two-phase time-averaged equations were then solved with the help of RNGk-εturbulence model.The coupling velocity and pressure equations were solved using the SIMPLE (Semi-implicit method for pressure-linked equations) algorithm and VOF (Volume of fluid) method was applied to track the flow surface.【Result】 The difference in discharges between the numerical simulation and the theoretical formula was small with relative error of less than 0.3%,indicating that the theoretical formula was correct.【Conclusion】 The flow discharge rate of the hyperbolic weir was proportional to the water head,which makes it easy to control and measure flow rate.

hyperbolic weir;flow coefficient;numerical simulation;discharge formula

网络出版时间:2016-07-1208:4510.13207/j.cnki.jnwafu.2016.08.031

2014-12-26

国家自然科学基金项目(51578452,51178391)；陕西省科学研究计划资助项目(2014K15-03-05)；陕西省工业科技攻关项目(2016GY-180)

魏文礼(1965-)，男，陕西大荔人，教授，博士，主要从事环境水力学、水污染控制理论与技术研究。

E-mail:wei_wenli@126.com

TV132.2

A

1671-9387(2016)08-0213-06

网络出版地址:http://www.cnki.net/kcms/detail/61.1390.S.20160712.0845.062.html