运用VBA技术仿真信号处理电路的研究
周 伟,李扬红,周建斌,赵 祥,杜 鑫
(1.成都理工大学 核技术学院,成都 610059; 2.东华理工大学 研究生院,南昌 330013)
运用VBA技术仿真信号处理电路的研究
周伟1,李扬红2,周建斌1,赵祥1,杜鑫1
(1.成都理工大学核技术学院,成都610059; 2.东华理工大学 研究生院,南昌330013)
提出了一种崭新的基于VBA技术的信号仿真方法。从实际信号处理电路的仿真出发,运用基尔霍夫电流定律,建立输入信号和输出信号之间的数学关系方程。方程解算过程中,利用数值微分算法求解,并建立输入、输出之间的数学关系模型。通过RC电路、CR电路以及成形滤波电路等实际核脉冲信号处理电路的仿真测试结果来看,运用VBA技术仿真信号处理电路的方法是可行的。
信号仿真;VBA技术;数值微分法;核信号处理
核脉冲信号的处理包括基于分立元件的模拟式处理和基于可编程微处理器的数字式处理。随着半导体技术的快速发展,核脉冲信号数字处理技术已经成为核技术领域的研究热点之一[1-2];而信号处理电路的软件仿真是整个数字式核脉冲信号处理过程中必不可少的环节之一,既可以验证算法模型的原理正确性,也能够初步完成系统性能指标的测试。目前,常用的电路仿真软件有Multisim、Proteus、Pspice等。这些软件功能丰富,既能够仿真测试电路的静态工作特性,如工作电压和工作电流等,又能够实时模拟电路的动态工作特性,如波形测量、逻辑分析等[3~6]。VBA技术(visual basic for application)是微软公司为工程应用而专门设计的一种可视化程序开发环境。将VBA技术和Excel应用相结合,不仅能够使用Excel提供的库函数,访问其特有的命令和结构,使用统计分析和图表绘制等功能,还可以创建自定义的用户界面[7-8]。
针对核脉冲信号数字成形处理的迫切要求,本文运用微分方程数值解算方法,建立CR微分成形、RC积分成形、Sallen-Key(下文简称SK)低通高斯成形等实际电路的数字成形模型,并借助于计算机VBA软件平台,完成了上述数字成形模型对标准信号和实际信号的仿真测试。
1 核信号基本成形电路的数值分析与模拟仿真
1.1RC积分成形电路
从电路原理上分析,RC电路是一个简易的低通滤波电路,在电子学线路中,主要用于前级输入信号的积分成形和消除放大电路的失调电压。经过RC积分成形后,信号的幅度会衰减,而脉宽会增大。图1是RC电路的连接图,图中R、C的参数选取一般由多次实验确定。
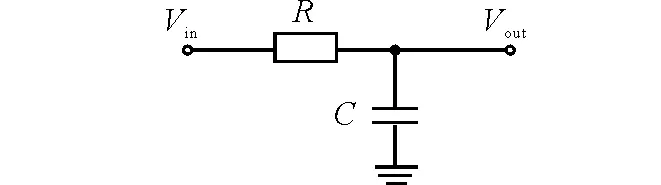
图1 基本的RC积分成形原理图
图1中,Vin为输入信号,Vout为输出信号,根据KCL定律(Kirchhoff Current Law),列出输入与输出之间的微分方程:
(1)
由于输入信号来源于核辐射探测器,是一个随机脉冲信号,不能用简单的数学函数描述,而且通过RC积分成形电路后,输入信号脉冲形状变化也需要研究人员的重点关注,因此,对于式(1)的求解采用常规连续函数的微分方程法是不合适的,需要在时间域内尝试新的微分数值法。
取足够小的时间间隔dt,则可以将Vin数字化为X(n),Vout数字化为Y(n),可以将式(1)变换为:
(2)
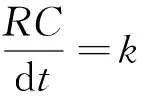
(3)
式(3)中,当前时刻的输出信号Y(n)既与当前时刻的输入信号X(n)有关,也与前一时刻输出信号Y(n-1)有关。从形式可以看出,式(3)是一个数值递推模型,可以通过循环迭代法计算。式(3)中,k是成形参数,控制输出信号的幅度和脉宽。在VBA软件平台中,首先,产生标准负指数的输入信号;然后,编写相应程序代码实现式(3);最后,调节参数k即可输出不能成形时间的输出心。图2是数字RC积分成形模型对标准负指数信号仿真模拟图。
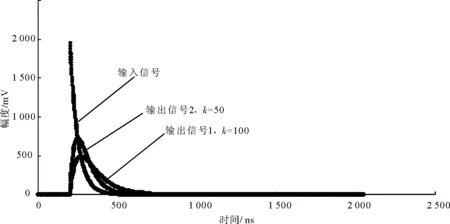
图2 数字RC积分成形模型的标准信号仿真模拟
1.2CR微分成形电路
从电路原理上分析,CR电路是一个简易的高通滤波电路。经过CR微分成形后,信号的幅度保持不变,而脉宽会变窄。图3是CR电路的连接图。
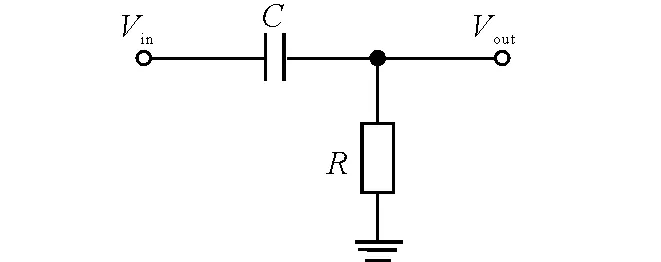
图3 基本的CR微分成形原理图
图3中,Vin为输入信号,Vout为输出信号,根据KCL定律,列出微分方程:
(4)
采用同样处理方法,将Vin数字化为X(n),Vout数字化为Y(n),n=0,1,2,…,将式(4)转换成:
(X(n)-X(n-1))-(Y(n)-Y(n-1))=
(5)

(6)
式(6)中,当前时刻的输出信号Y(n)既与当前时刻的输入信号X(n)有关,也与前一时刻输出信号Y(n-1)和输入信号X(n-1)有关。从形式可以看出,式(6)也是一个数值递推模型,k是成形参数,控制输出信号的脉宽。采用同样的方法,在VBA软件平台中,数字CR微分成形模型的仿真模拟如图4所示。
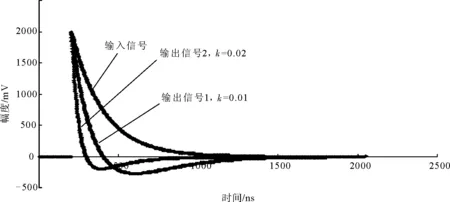
图4 数字CR微分成形模型的标准信号仿真模拟
采用微分数值法研究RC积分电路与CR微分电路的数字化,经过理论推导,最终的数字成形模型是一个数值递推解,并由相应的成形参数控制输出信号。借助于VBA软件平台,完成了对数学模型的仿真模拟。对比仿真结果和实际测试,验证了所研究的数值递推模型的正确性。
1.3S-K滤波器
S-K滤波器是一种信号处理中常用的有源滤波电路,它有高通S-K滤波器和低通S-K滤波器两种形式[9-10]。在核电子学中将低通S-K滤波器广泛应用于核脉冲信号的滤波成形,可以在较少的级数下得到近似高斯波形的输出。图5是低通S-K滤波器电路原理图。
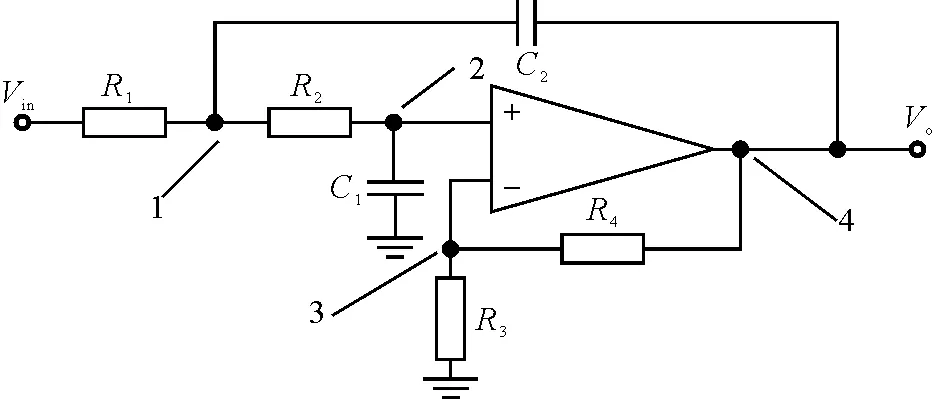
图5 低通S-K滤波器电路原理图
1) S-K滤波器的微分数值分析
类比RC积分成形与CR微分成形电路的分析方法,将低通S-K滤波器进行数值分析,图5中标记4个节点(节点1~4),分别标识对应的电压Vf,Vp,Vn和Vo。根据KCL定律等,可以建立如下四个传递公式:
(7)
(8)
(9)
Vn=Vp
(10)
式(7)~式(10)中,为了简化推导,取R1=R2=R3=R4=R,C1=C2=C,再合并同类项后,则式(7)~式(10)可以联合推导得:
(11)
式(11)中,将Vin数字化为X(n),Vout数字化为Y(n),则可得到:
(RC)2Y''(n)+RCY'(n)+Y(n)=2X(n)
(12)
因此,基于S-K滤波器的高斯成形模型可以归纳为一个Y(n)=f(X(n))数学递推模型。由式(12)可知,该函数是一个非齐次二次微分方程的根。采用数值微分法将式(12)变换为:
(13)
将式(13)进行合并整理后,得:
(14)
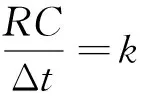
(1+k+k2)yn+1=(k+2k2)yn-k2yn-1+2x
(15)
根据式(15)可以得到:
综上所述,核脉冲信号的数字高斯成形后的输出信号可以通过式(16)递推调用实现。其中,k表示高斯成形输出信号的调整参数。
2)数字高斯滤波的仿真
在核能谱测量仪器中,核辐射探测器的输出信号先进行噪声的滤波处理,再将负指数信号成形成信噪比更高的高斯脉冲信号,以便后续电路的处理得到高分辨率的能谱图(脉冲幅度谱)。经仿真测试,输入负指数信号的衰减常数τ=100,噪声信号由随机函数产生叠加在输入信号上,输入信号的SNR=10 dB,3种参数成形后输出信号的SNR都超过了40 dB。
3) 实测探测器输出信号的数字高斯成形仿真
在仿真标准指数信号和相应的数字高斯成形的基础上,又对实际的核脉冲信号进行了数字高斯成形模型的仿真。仿真实测的核脉冲信号是用美国Moxtek公司的Si-PIN半导体探测器XPIN-BT测量55Fe核素的输出信号经过高通滤波、线形放大、高速ADC采样后得到的信号。图6是不同成形参数条件下实测核脉冲信号的数字高斯成形仿真图(20 MHz采样率)。
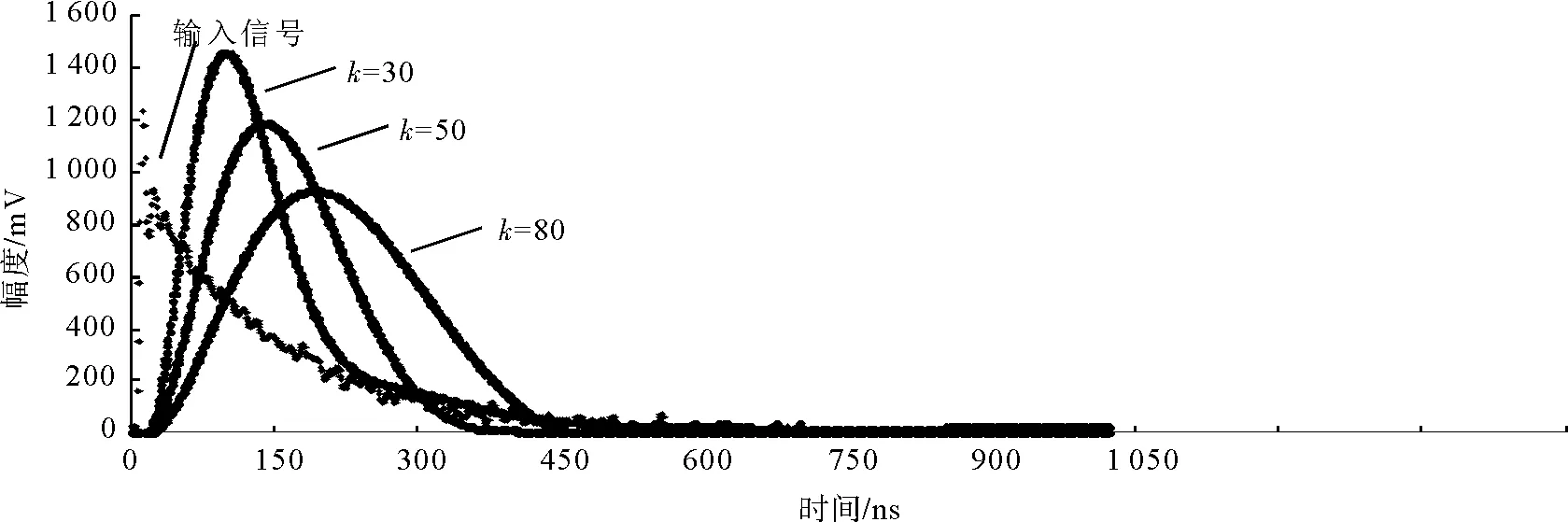
图6 不同成形参数条件下实际核脉冲信号的数字高斯成形仿真
2 结束语
在信号处理电路的仿真测试中引入VBA技术是一次成功的尝试。以KCL定律为基础,运用数值微分法探讨实际信号处理电路的数字模型是本研究的关键。本文先后研究了CR微分成形、RC积分成形和S-K高斯成形等实际电路的数学模型,并完成了标准负指数信号和实际核脉冲信号的仿真测试。测试结果显示所研究数字成形模型的正确性。此外,可以预见,随着实时高速采样技术的快速发展,采样的最小时间单元可以微分到皮秒量级(部分可以达到飞秒量级),从而更加缩小离散系统与连续系统的时间界限。鉴于在时间域内的模型简单、概念清楚、易于实现、对比直观等优点,数值微分法对于完善离散系统的时域分析方法必将会有极大的促进。
下一步将继续运用数值微分法研究更多实际信号处理电路的数字模型,结合仿真测试和硬件实现,完善研究方法;研究连续系统内数值微分法的应用,探讨可能存在的应用不足。
[1]王经瑾,范天民,钱永庚.核电子学[M].北京:原子能出版社,1983.
[2] 王芝英,楼滨乔,朱俊杰,等.核电子技术原理[M].北京:原子能出版社,1989.
[3] 薛山.Matlab基础教程[M].北京:清华大学出版社,2011.
[4] 刘维.精通Matlab与C/C++混合程序设计[M].3版.北京:北京航空航天大学出版社,2012.
[5] 王连英.基于Multisim10的电子仿真试验与设计[M].北京:北京邮电大学出版社,2013.
[6] 周润景.基于PROTEUS的电路及单片机设计与仿真[M].2版.北京:北京航空航天学出版社,2010.
[7] 谭浩强.Visual Basic程序设计[M].3版.北京:清华大学出版社,2012.
[8] 谭浩强.QBasic语言教程[M].2版.北京:电子工业出版社,2002.
[9] ZHOU J B,ZHOU W,LEI J R,et al.Study of time-domain digital pulse shaping algorithms for nuclear signals[J].Nuclear Science & Techniques,2012,23(3):150-155.
[10] 李东仓,杨磊,田勇,等.基于Sallen-Key滤波器的核脉冲成形电路研究[J].核电子学与探测技术,2008,28(3):563-566.
Study of Signal Simulating for Actual Circuit Based on VBA Technique
ZHOU Wei1,LI Yanghong2,ZHOU Jianbin1,ZHAO Xiang1,DU Xin1
(1.School of Nuclear,Chengdu University of Technology,Chendu 610059,China;2.School of Postgraduates,East China Institute of Technology,Nanchang 330013,China)
A novel signal simulating method based on VBA technique is presented in this paper.Depending on the actual circuit of signal processing,mathematical equations between the input signal and the output signal are established according to the Kirchhoff Current Law.After equations reducing,a mathematical model between the input and output is also built by using the numerical differential method.And then,some simulating works of actual circuits are implemented such as RC integral,CR differential and Gaussian shaping circuit.The simulating results show that VBA technique applied in signal processing circuit simulating is feasible.
signal simulating; VBA technique; numerical differential; nuclear signal processing
2014-10-15;修改日期: 2014-11-10
成都理工大学教学骨干教师计划资助(JXGG201409);四川省卓越工程师教育培养计划(14Z003-31)。
周伟(1979-),男,博士,副教授,主要从事核方法与核仪器仪表方面的研究。
TP391.9;TN784
A
10.3969/j.issn.1672-4550.2016.01.007

