基于关键变量的OPLS预测方法
罗明英, 王 帆, 谭 帅, 侍洪波
(华东理工大学化工过程先进控制和优化技术教育部重点实验室,上海 200237)
基于关键变量的OPLS预测方法
罗明英,王帆,谭帅,侍洪波
(华东理工大学化工过程先进控制和优化技术教育部重点实验室,上海 200237)
产品的最终质量主要是由生产过程中的关键变量决定的,因此,回归模型的质量预测能力与过程变量的选择密切相关。本文提出了一种新的基于关键变量(CV)的OPLS预测方法(CV-OPLS),用于输出变量较多过程的质量预测。首先,根据关键变量选取准则,为每个质量变量选取建模所需的关键过程变量。为了减少最后需要建立的模型个数,将由质量变量及其相应的关键过程变量组成的数据阵进行重组,并用OSC算法去除重组后的数据阵中与质量变量无关的干扰信息。然后,对校正后的数据阵建立PLS模型,求取相应的模型回归系数,得到最终的质量预测结果。与传统的PLS及OPLS方法相比,该方法能够在保证模型较好预测精度的前提下,有效地简化模型结构。最后,通过Tennessee Eastman(TE)过程的实验仿真验证了CV-OPLS方法的有效性。
回归模型; 关键变量; OPLS算法; 质量预测
过程数据分析的一个主要任务是从经验或历史数据中建立回归模型并用于产品的质量预测。近年来,多元回归建模技术迅速发展,已被成功用于定量化提取自变量与因变量之间的因果关系,例如主成分回归(PCR)[1]、偏最小二乘(PLS)[2-3]、独立成分回归(ICR)[4]等。其中,PLS方法是一个广为人知并应用成熟的有效工具。PLS可以有效地解决变量相关的问题,适用于变量较多且耦合严重的工业过程建模[5],并广泛应用于过程监控和故障诊断等领域[6-7]。随后,很多复杂的、扩展的最小二乘方法也被提出并加以利用,如文献[8]提出的针对多阶段间歇过程的两层PLS方法; 文献[9]提出的针对非线性和时变化工过程的选择性集成局部偏最小二乘算法(SELPLS)等。
回归模型预测能力的好坏与过程变量的选择密切相关。作为一种重要的知识提取工具,变量选择的重要性已在许多文献中作了相应的阐述[10-11]。产品的最终质量主要是由生产过程中的关键变量决定的,与质量无关的过程变量的变化对于质量预测来说是系统波动噪声,它们的波动会引起回归模型质量预测精度下降,建模前应当把它们剔除。目前已有的关键变量选取策略有:前向选取、后向选取、步进回归等[12-13],采用的方法都是逐一搜索所有可能的过程变量。这些方法在过程变量较多的情况下会造成巨大的计算负担,不利于实际应用。为了克服上述方法的缺陷,文献[14]提出了一种新的关键变量选择策略,能够简单、有效地从回归模型中剔除那些与质量无关的过程变量,达到简化模型结构并提高预测精度的目的。对于输出变量较多的生产过程来说,每个质量变量建模所需的关键过程变量一般是不同的,在为它们挑选完关键过程变量后,为了得到每个质量变量的预测结果,需建立多个不同的回归模型。这样虽然减少了每个模型的建模所需变量,但是却增加了最后所需建立的回归模型个数,计算复杂度也相应增加,不利于实际生产中的应用。
此外,在多变量过程数据X中通常都包含与质量变量Y不相关的系统变化,这些变化对Y的预测没有帮助。为了改进这个问题,Wold等[15]提出了正交信号修正(OrthogonalSignalCorrection,OSC)算法,基本思想是去除X中与Y正交的变化,之后对修正后的X数据进行PLS回归,从而得到更好的PLS模型。Trygg等[16]提出了基于非线性迭代偏最小二乘(NonlinearIterativePartialLeastSquares,NIPALS)算法[17]的正交PLS(OPLS)算法,不需要迭代计算,从而使计算量大大减少。本质上来说,OPLS是一种预处理算法,将数据X中与Y无关的成分滤除。对于被过滤数据X的PLS建模可以得到更为简单的模型。
鉴于此,本文提出了一种新的基于关键变量的OPLS建模方法(CV-OPLS),用于输出变量较多的过程质量预测。首先,根据关键变量选取准则,为每个质量变量选取其建模所需的关键过程变量。按照重组关键变量矩阵的方法,将由质量变量及其相应的关键过程变量组成的数据阵进行重新整合,并用OSC算法去除重组后的数据阵中与质量变量无关的干扰信息。然后,对校正后的数据阵建立PLS模型,求取相应的模型回归系数,得到最终的质量预测结果。与传统的PLS及OPLS建模方法相比,该方法能够在保证模型较好预测精度的前提下,有效地简化预测变量组以及减少模型个数。最后,通过TennesseeEastman(TE)过程的质量预测仿真,验证了该方法应用于过程建模及质量预测的有效性和优越性。
1 OPLS方法简介
OSC算法的基本思想是:在使过程变量x与质量变量y相关时,提前剔除自变量中那些与因变量相关性较小甚至不相关的数据信息,即采用正交投影的方法从x中剔除与y正交的量。将OSC与PLS方法相结合,即OPLS算法。Trygg等[16]提出了改进的OPLS算法,其正交成分可直接通过NIPALS算法得到,可以减少计算量,避免模型出现过度拟合的现象。具体方法步骤如下(以单输出变量为例,多输出变量的情况类似可得):
首先将原始数据进行归一化处理,得到数据阵{x,y}。
(1) 计算权值向量:wΤ=yΤx/(yΤy);
(2) 将w归一化:w=w/‖w‖;
(3)t=xw/(wΤw);
(4)PΤ=tΤx/(tΤt);
(5) w⊥=p-w;
(6) 将w⊥归一化:w⊥=w⊥/‖w⊥‖;
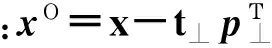
将正交信号校正后的xΟ与y组成为新的数据阵{xΟ,y},带入线性PLS算法以建立回归模型。假设两者具有以下的线性相关性:
(1)
其中:H为模型误差矩阵;C为回归系数矩阵,可通过NIPALS算法[17]得到。
(2)
式中:P和Q分别为X和Y的负载矩阵; W为x的权系数矩阵。于是对于新样本xnew的回归预测值为
(3)

2 基于关键变量的OPLS建模方法
2.1方法简介
传统的PLS方法在建模时没有进行过程变量的选取,将那些与质量无关的过程变量的变化引入回归模型,会造成质量预测精度的下降。同时,考虑到对于输出变量较多的生产过程来说,每个质量变量建模所需的关键过程变量一般是不同的,因此,有必要在建模前为每个质量变量挑选相应的关键变量。
一般的PLS方法只是建立一个回归模型进行质量预测。本文为了增强模型中过程变量与质量变量之间的因果关系,提高预测精度,先为每个质量变量挑选其建模所需的关键过程变量,然后再分别建模进行回归预测。由于每个质量变量挑选出的关键变量一般是不同的,所以最后得到的由每个质量变量与其相应的关键变量组成的数据阵也不同。为了得到每个质量变量的预测结果,需要建立多个回归模型进行预测。这样虽然简化了每个模型的预测变量组,但是却增加了最后所需建立的回归模型的个数,计算复杂度也相应地增加,不利于实际生产中的应用。本文提出了一种将关键变量矩阵进行重新组合的方法,能够在保证模型有较好预测精度的同时,尽量简化模型以及减少模型个数。
2.2选取关键变量
假设训练数据阵{X(n×m),Y(n×d)}已去均值标准化,其中,n为样本个数,m为过程变量个数,d为质量变量个数。为每一个质量变量挑选建模时所需的关键过程变量。
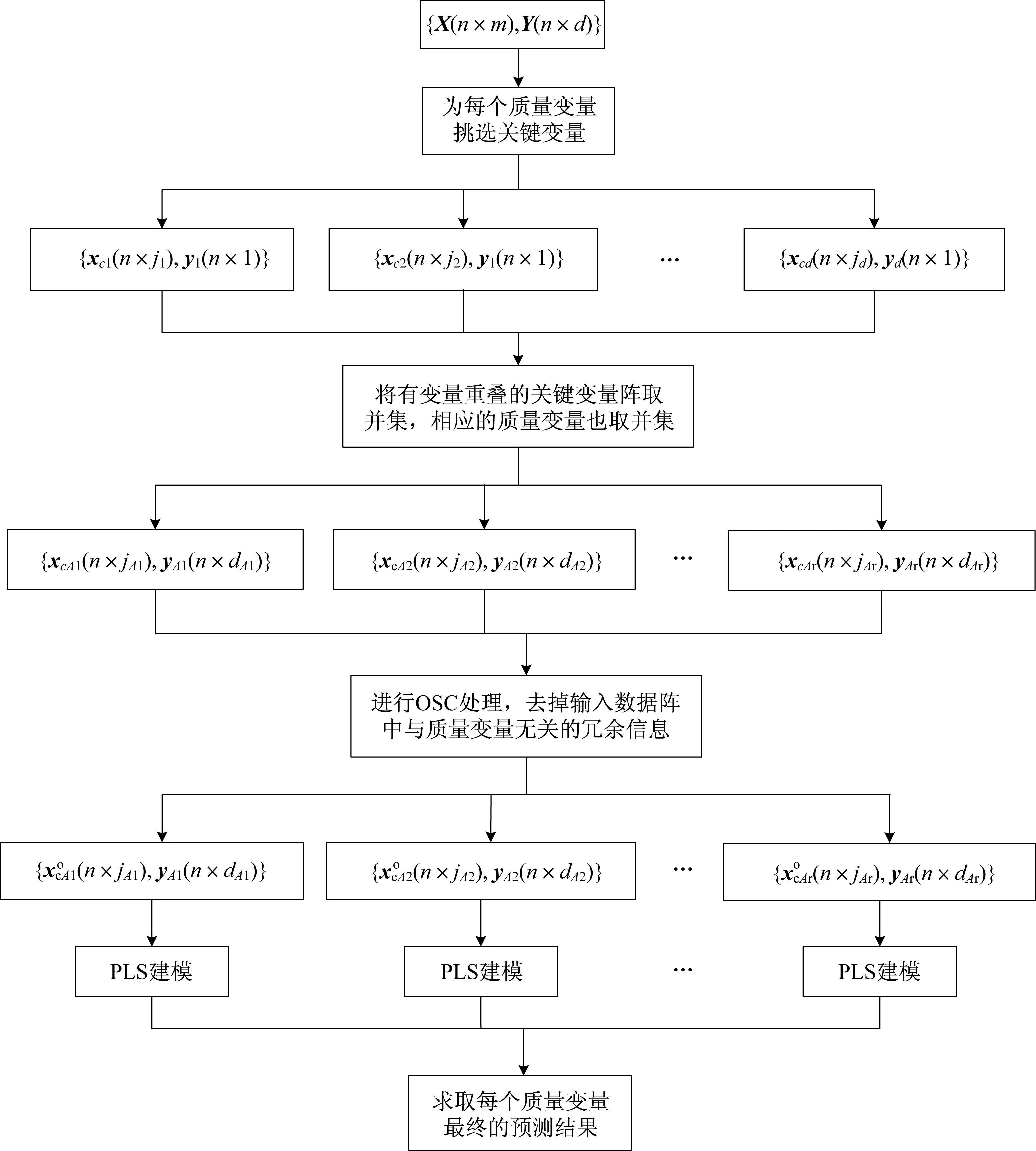
首先定义每个过程变量xj(n×1)(对应X(n×m)的第j列)对于第k个质量变量yk(n×1)(对应Y(n×d)的第k列)的相关贡献率指标[14]如下:
(4)
其中:下标j表示过程变量; k表示质量变量; 函数r()计算了2个变量间的相关系数。
此外,仅仅依据相关贡献率指标并不能确切可靠地表征模型的预测能力。为了进一步评估这些过程变量的质量预测能力并最终确认它们是否应该作为关键变量用于回归建模,引入验证回归模型能力的预测均方误差指标[18]:
(5)


(3) 将排序后的过程变量一个一个循环加入到建模变量中,并依次计算得到新的PLS回归模型。为了简单起见,每次回归模型中统一保留2个潜成分即可。利用测试数据求取新的MSEk值,并与之前没有加入该变量时的预测精度进行对比,如果MSEk指标下降,说明该变量的加入有助于改善模型的预测能力,则保留该过程变量为关键建模变量,继续搜索下一个过程变量; 否则停止,在此之前的回归模型作为最终的质量预测模型。
通过上述变量选择步骤,最终为每个质量变量仅仅保留它所需的少数的关键过程变量,消除了无关因素的不利影响,达到了简化回归模型的目的,并强调了回归模型的泛化预测能力。
2.3重组关键变量矩阵
按照上述挑选关键变量的方法,即可得到每个质量变量相应的关键变量矩阵。以第k(1≤k≤d)个质量变量为例,假设其相应的关键变量矩阵为xck(n×jk),其中,jk代表关键变量个数。这样就得到d组不同数据阵,分别为{xc1(n×j1),y1(n×1)},{xc2(n×j2),y2(n×1)},…,{xcd(n×jd),yd(n×1)}。如要得到每个质量变量的预测结果,就需建立d个不同的回归模型进行预测。为了在保证模型有较好预测精度的同时,尽量简化模型以及减少模型个数,本文提出根据每个关键变量矩阵的变量重叠程度对其进行重组的设想。
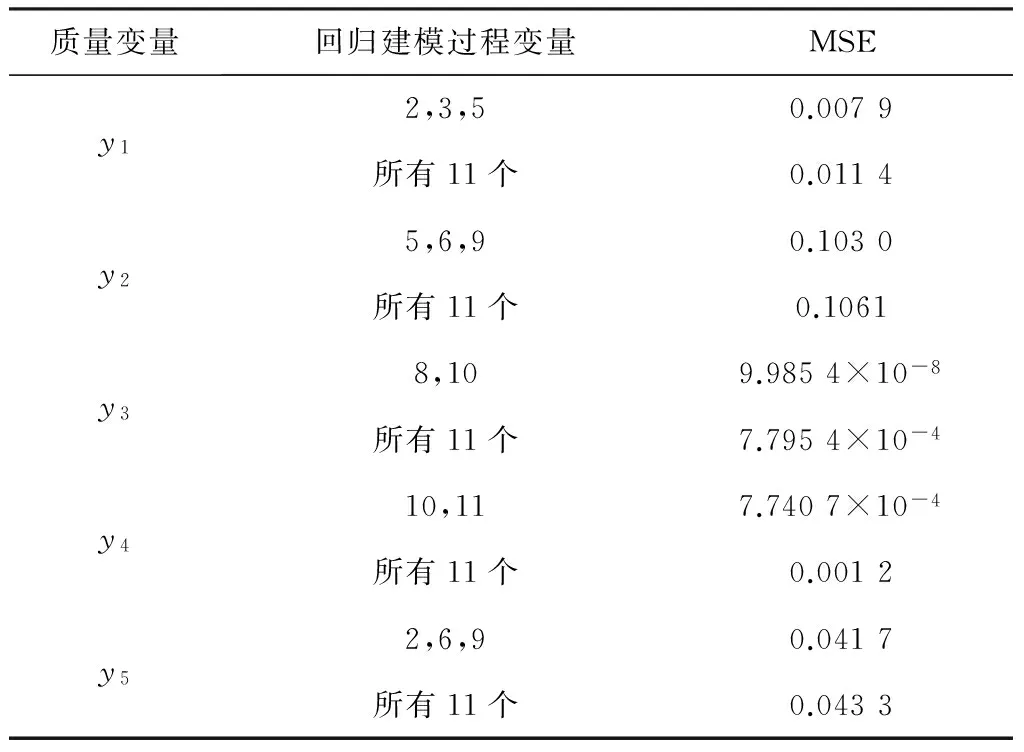
首先,对每个关键变量矩阵xc1(n×j1),xc2(n×j2),…,xcd(n×jd)的变量组成进行观察,将其中有变量重叠的矩阵放在一起,对矩阵中关键变量求并集,组成新的个数更少的关键变量矩阵xcA1(n×jA1),xcA2(n×jA2),…,xcAr(n×jAr),同时,将其相应的质量变量也并在一起,组成新的质量变量矩阵yA1(n×dA1),yA1(n×dA2),…,yAr(n×dAr)。然后,就可以将重组后的关键变量矩阵xcA1,xcA2,…,xcAr与其相应质量变量矩阵yA1,yA1,…,yAr组成r组新数据阵,即{xcA1(n×jA1),yA1(n×dA1)},{xcA2(n×jA2),yA1(n×dA2)},…,{xcAr(n×jAr),yAr(n×dAr)},其中,r(r 举例说明,假设y1相应的关键变量矩阵xc1=[x1,x2,x3],其中x1,x2,x3分别对应原输入变量矩阵X(n×m)的第1,2,3列; y2相应的关键变量矩阵xc2=[x2,x3,x4],其中x2,x3,x4分别对应原输入变量矩阵X(n×m)的第2,3,4列。xc1,xc2中都包含第2和第3个过程变量,把这2个关键变量矩阵并在一起,得到一个新的关键变量矩阵xcA1=[x1,x2,x3,x4]。同时,将其相应的质量变量y1,y2也并在一起,得到一个新的质量变量矩阵yA1=[y1,y2]。此时,就将原先的两组数据阵{xc1,y1}和{xc2,y2}重组成了一组新的数据阵{xcA1,yA1}。 按照上述将关键变量矩阵进行重新组合的方法,最终得到的数据阵组数会大大减少,那么,所需建立的回归模型个数也会相应减少。另外,考虑到由于关键变量矩阵的重组可能会造成模型预测精度下降的问题,在最后建模前,先对每组数据阵进行OSC预处理,去除关键变量矩阵中与输出质量变量不相关的冗余成分,进一步增强模型中关键变量对质量变量的解释能力,以达到既简化模型结构又保证模型预测精度的目的。 本文采用复相关系数R2指标[19]来评估回归模型的预测性能。其计算公式为 (6) 4.1实验设置 将本文提出的方法应用于TE过程的质量预测中,并与传统的PLS及OPLS方法进行对比,验证该方法的有效性。为了公平地对比各种方法的预测性能,仿真过程中每种方法的训练集和测试集以及挑选的潜变量个数都相同。 4.2TE过程简介及实验数据选取 TE过程是一个典型的多变量复杂化工生产过程,目前已被广泛作为控制算法的测试和性能评估的仿真平台[20-22]。该过程主要由5个操作单元组成,分别为:连续搅拌式反应釜、冷凝器、气液分离塔、汽提塔和离心式压缩机。过程包括12个控制变量、22个连续测量变量和19个非连续测量成分变量。仿真过程中的采样间隔均为3 min。本文选取的训练集和测试集分别为两组正常数据,每组数据包含500个采样点。11个控制变量作为回归建模的输入数据阵,实验中分析的质量变量来自于22个连续测量变量,选取其中对于整个反应过程具有重要意义的5个变量作为模型的输出[23]。具体的输入、输出实验数据选取结果如下:x1,物流A进料量,kmol/h;x2,物流D进料量,kmol/h;x3,物流E进料量,kmol/h;x4,物流A、C总进料量,kmol/h;x5,压缩机回收阀开度,%;x6,排放阀开度,%;x7,分离器罐液流量,kmol/h;x8,汽提器液体产品流量,kmol/h;x9,汽提器水流阀,%;x10,反应器冷水流量,m3/h;x11,冷凝器冷却水流量,m3/h;y1,物料A流量,kmol/h;y2,排空速率,r/min;y3,汽提塔液位,%;y4,汽提塔底部流量,kmol/h;y5,汽提塔上部蒸汽流量,kmol/h。 图1 CV-OPLS方法示意图Fig.1 Illustration of the CV-OPLS method 4.3预测模型仿真及结果分析 图2 关键变量选择的CV指标Fig.2 CV criterion of critical variable selection表1 y5的关键变量选择结果 Table 1 Critical variable selection result of y5 序号回归建模过程变量MSE190.04188826,90.04179232,6,90.0416744所有11个0.043304 按照相同的方法依次计算出所有质量变量的关键变量选择结果,结果如表2所示。 表2 关键变量选择结果 通过对表2中每个关键变量矩阵的变量组成进行观察,发现y1,y2,y5这3个质量变量所对应的关键变量有重叠,因此把它们放在一起求并集,组成一组新的关键变量矩阵和质量变量矩阵。同理,y3和y4这两个质量变量相应的关键变量有重叠,也把它们并在一起进行重组。这样最后就只得到2组关键变量矩阵和相应的质量变量矩阵,具体的重组结果见表3。 表3 重组后的关键变量选择结果 为了进一步提高每对数据阵中x对y的解释能力和相关度,对于重组后的两组数据阵{x(500×5),y(500×3)}和{x(500×3),y(500×2)},在进行PLS建模前先对其进行OSC预处理,然后再将校正后的数据阵分别带入PLS算法进行回归分析,求取每个质量变量最终的预测结果。为了验证CV-OPLS方法的有效性,表4给出了其与传统的PLS及OPLS方法的预测性能对比结果,表中黑体表示预测结果的最优值。 表4 不同方法的预测性能指标结果 对比表4中3种建模方法的R2指标,可以看出3种方法均可取得较好的预测效果。由于本文提出的CV-OPLS方法能够剔除对于质量预测贡献较小的过程变量,过滤掉无关的冗余信息,并大大减少所需建立的回归模型个数,因此比传统的PLS及OPLS模型更简单实用,而且精度可靠。 此外,为了彰显本文所提方法的先进性,表5给出了CV-OPLS方法与OPLS方法在线预测时算法执行时间的对比结果。 从表5中可以看出,两种方法都能取得较为满意的算法执行效率。虽然本文提出的CV-OPLS方法在离线建模时比传统的OPLS方法的算法略显复杂,但在线应用时,两者的算法执行时间相差不大。由于CV-OPLS方法可以获得更高的预测精度,所以比传统的OPLS方法更为实用。 表5 不同算法的执行时间对比结果 图3给出了CV-OPLS方法对实验中测试集的质量预测仿真结果。 本文提出了一种新的回归建模方法(CV-OPLS),应用于多输出变量过程的关键变量选择及质量预测。与传统的PLS建模方法相比,该方法能够有效地简化预测变量组,为每个质量变量仅保留建模所需的关键过程变量,增强了过程变量与质量变量之间的因果关系,并强调了模型的泛化能力。同时,该方法大大减少了最后需要建立的回归模型个数,并在建模前去除了关键变量中与质量变量无关的干扰成分,保证了回归模型较好的预测精度。此外,通过对Tennessee Eastman (TE)过程的实验仿真,比较了本文提出的CV-OPLS算法和传统的PLS算法对TE过程多输出变量情况下的回归建模预测效果,实验表明CV-OPLS方法不仅模型结构简单实用,而且具有较好的拟合能力和泛化的预测能力。 图3 CV-OPLS方法的质量预测结果Fig.3 Quality prediction results of the CV-OPLS method [1]GE Zhiqiang,SONG Zhihuan,GAO Furong.Mixture probabilistic PCR model for soft sensing of multimode processes[J].Chemometrics and Intelligent Laboratory Systems,2011,105 (1):91-105. [2]HOSKULDSSON A.PLS regression methods[J].Journal of Chemo-metrics,1998,2 (3):211-228. [3]FACCO P,DOPLICHER F,BEZZO F,etal.Moving average PLS soft sensor for online product quality estimation in an industrial batch polymerization process[J].Journal of Process Control,2009,19 (3):520-529. [4]GE Zhiqiang,SONG Zhihuan,WANG Peiliang.Probabilistic combination of local independent component regression model for multimode quality prediction in chemical processes[J].Chemical Engineering Research and Design,2014,92 (3):509-521. [5]JIA Runda,MAO Zhizhong,WANG Fuli.KPLS model based product quality control for batch processes[J].CIESC Journal,2013,64 (4):1332-1339. [6]GODOY J L,VEGA J R,MARCHETTI J L.A fault detection and diagnosis technique for multivariate processes using a PLS-decomposition of the measurement space[J].Chemometrics and Intelligent Laboratory Systems,2013,128(15):25-36. [7]HU Yi,MA Hehe,SHI Hongbo.Robust online monitoring based on spherical-kernel partial least squares for nonlinear processes with contaminated modeling data[J].Industrial & Engineering Chemistry Research,2013,52 (26):9155-9164. [8]GE Zhiqiang,SONG Zhihuan,ZHAO Luping,etal.Two-level PLS model for quality prediction of multiphase batch processes[J].Chemometrics and Intelligent Laboratory Systems,2014,130(2):29-36. [9]SHAO Weiming,TIAN Xuemin.Adaptive soft sensor for quality prediction of chemical processes based on selective ensemble of local partial least squares models[J].Chemical Engineering Research and Design,2015,95:113-132. [11]MEHMOOD T,LILAND K H,SNIPEN L,etal.A review of variable selection methods in partial least squares regression[J].Chemometrics and Intelligent Laboratory Systems,2012,118 (3):62-69. [12]KLEINBAUM D G,KUPPER L L.Applied Regression Analysis and Other Multivariable Methods[M].Third Edition.Beijing:China Machine Press,2003. [13]KUTNER M H,NACHTSHEIM C J,NETER J.Applied Linear Regression Models[M].Fourth Edition.Beijing:Higher Education Press,2005. [14]赵春晖.多时段间歇过程统计建模、在线监测及质量预报[D].沈阳:东北大学,2008. [15]WOLD S,ANTTI H,LINDGREN F.Orthogonal signal correction of near-infrared spectra[J].Chemometrics and Intelligent Laboratory Systems,1998,44 (1):175-185. [16]TRYGG J,WOLD S.Orthogonal projection to latent structures (O-PLS)[J].Journal of Chemometrics,2002,16 (3):119-128. [17]DAYAL B S,MACGREGOR J F.Improved PLS algorithms[J].Journal of Chemometrics,1997,11 (1):73-85. [18]ZHAO Chunhui,GAO Furong.Multiphase calibration modeling and quality interpretation by priority sorting[J].Chemical Engineering Science,2011,66 (21):5400-5409. [19]ZHAO Luping,ZHAO Chunhui,GAO Furong.Phase transition analysis based quality prediction for multi-phase batch processes[J].Chinese Journal of Chemical Engineering,2012,20 (6):1191-1197. [20]DOWNS J H,VOGEL E F.A plant-wide industrial process control problem[J].Computers Chemical Engineering,1993,17 (3):245-255.. [21]DONG Jie,ZHANG Kai,HUANG Ya,etal.Adaptive total PLS based quality-relevant process monitoring with application to the Tennessee Eastman process[J].Neurocomputing,2015,154:77-85. [22]LAU C K,KAUSHIK GHOSH,MOHD A H.Fault diagnosis of Tennessee Eastman process with multi-scale PCA and ANFIS[J].Chemometrics and Intelligent Laboratory Systems,2013,120(2):1-14. [23]杜万亮.基于独立成分分析的多元回归方法研究[D].沈阳:东北大学,2009. OPLS Prediction Method Based on Critical Variables LUO Ming-ying,WANG Fan,TAN Shuai,SHI Hong-bo (Key Laboratory of Advanced Control and Optimization for Chemical Processes,Ministry of Education,East China University of Science and Technology,Shanghai 200237,China) The final quality of product is mainly decided by those critical variables in production process,so the quality prediction ability is closely dependent on the selected process variables.This paper proposes a critical-variable-based OPLS prediction method,CV-OPLS model,for the quality prediction of industrial processes with multi output variables.First,according to the selection criteria of critical variables,we choose critical process variables for each quality variable in modeling.In order to reduce the number of final models,the data matrix composed of quality variable and its critical variables is recombined,in which disturbing variation irrelevant with quality variable will be removed by means of OSC method.And then,PLS models are formed on the corrected data matrix,and the regression coefficients are computed such that the final quality prediction results are obtained.Compared with the traditional PLS and OPLS,the proposed method can effectively simplify model structure and attain superior prediction performance.Finally,the feasibility and effectiveness of the CV-OPLS method are further verified through experiments in Tennessee Eastman (TE) process. regression model; critical variable; OPLS method; quality prediction 1006-3080(2016)04-0529-08 10.14135/j.cnki.1006-3080.2016.04.014 2015-10-12 国家自然科学基金(61374140,61403072) 罗明英(1990-),女,河南禹州人,硕士生,主要研究方向为故障检测、诊断及工况监控。 通信联系人:侍洪波,E-mail:hbshi@ecust.edu.cn TP277 A3 基于CV-OPLS的质量预测
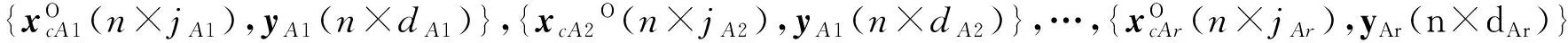

4 实验仿真
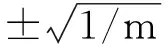





5 结 论


