基于粗糙集的矿井环境安全因素综合评价

孙玉洁, 王文庆

(西安邮电大学 a.通信与信息工程学院; b.自动化学院，西安 710061)



基于粗糙集的矿井环境安全因素综合评价

孙玉洁a, 王文庆b

(西安邮电大学 a.通信与信息工程学院; b.自动化学院，西安 710061)

总结了粗糙集在环境科学与环境工程研究领域的国内相关研究，并进一步针对传统煤矿安全监测系统中存在的不够客观的问题，基于粗糙集理论并使用信息熵的理论计算安全因素综合权重的方法,对于矿山井下环境中CO、H2S、粉尘等安全性因素做出更加客观的、合理的综合评价,以使更多学者了解和运用粗糙集理论和方法,进而推进该理论在环境领域的应用.

粗糙集；信息熵；综合权重

由于地下矿山的环境非常复杂，加之井下生产设备和工作人员数量庞大，整体的安全生产基础比较薄弱[1]，导致各类安全问题日益突出.国家统计数据显示，安全形势依然严峻[1]，因此矿山井下环境安全性的综合评价作为矿山安全性管理的重要环节,是不断提高矿山井下环境安全质量的重要保证[2-3].

粗糙集理论在改进和强化矿山安全生产工作方面的作用愈来愈明显，例如：矿山安全监测系统[1].如文献[4]讨论的是粗糙集结合神经网络在矿山地质环境影响评价模型及应用领域.如文献[5]提出的同样是一种基于RS-RBF网络(粗糙集和神经网络)复合在水环境质量评价领域的方法，其结合粗糙集理论对水质监测评价后的结果更加科学且可广泛应用于环境保护与污染治理的相关领域.在室内环境评价方面，主观评价是重要评价方法之一，该评价同样涉及有大量具有不确定性和不完备性的信息，结合粗糙集理论可从诸多主观评价指标中找出其中的关键指标，以使得在保留信息的完整性的同时能够减小计算量.如文献[6-7]均研究了在在室内环境舒适评价方法,先应用粗糙集理论约简不必要的属性，然后确定权重系数，进而在此基础上进行模糊变换计算出评价集，但是文献[7]仍然是基于主观的评价来找出总体评价中重要的影响指标.然而，以上的研究主要是基于主观上的评价方法进行的分析，不足以客观地作出评价，所以仅限于基本的粗糙处理办法的监测系统是难以作出有效决策的，应该结合其他方法对数据进一步有效挖掘.

本文结合粗糙集理论设计了一个矿井环境安全因素综合评价模型，通过对矿山井下环境安全性综合评价指标体系的属性进行约简，结合条件熵客观的确定了评价指标体系中的各个评价指标的权重，以及使用主观权重对矿山井下环境安全性水平进行了综合评价以实现客观评价，进而可以对井下环境安全性指标的数据进行有效挖掘，最终可依据公正客观的评价结果采取相应合理的安全措施，例如预警等提示.

1　粗糙集理论及评价模型

1.1粗糙集

粗糙集理论是Z.Pawlak于1982年提出的一种处理模糊和不确定知识的数学工具.它是继模糊集之后又一进展，与模糊集不同的是它不需要任何的主观知识，可以在保持分类能力不变的前提下，通过知识约简，导出问题的决策或分类规则.

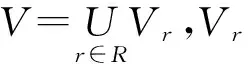
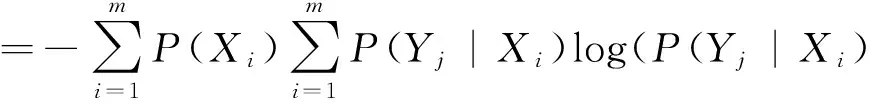
若S=(U,R,V,f)是一个决策系统，其中C∪D=R，C为条件属性集，D为决策属性，A集合属于C集合，则任意属性xi=C-A的重要性SGF(xi,A,D)=H(D|A)-H(D|A∪{xi}).

当A=Ø时，SGF(xi,A,D)=H(D)-H(D|{xi})称为xi属性和决策D的互信息.记为I(xi，D)[8，11-12].

1.2建立关系数据模型

为了结合粗糙集理论来对矿山井下各个安全因素进行综合评价，需要将各安全因素视为评价指标.为了保证客观、合理地对各个指标进行评价，首先建立相应的关系数据模型，即计算并确定每个指标的权系数，将这些评价指标视为条件属性[13]，则条件属性集合C={c1,c2,…，cm}，决策属性集合D={y}.实际应用中，可通过专家对每个评价指标打分后的最后综合得分y最终确定决策属性[14-15].

1.2.1评价指标权重的确定

影响地下矿井环境安全因素有很多，在本文研究的地下矿山生产中，主要的指标如表1所示.

表1　地下矿井环境安全因素指标体系

将信息观下的基于条件熵的权重αi与主观权重βi结合起来，得到决策系统的综合权重wi=μβi+(1-μ)αi(0μ1)，其中μ为主观因子，它由决策者以个人经验所决定.μ越小说明决策者越重视客观权重，μ越大越重视主观权重.

1.2.2综合评价模型

(1)构建信息系统S=(U,R,V,f)，其中U为待评价的作业区的集合，评价体系中的指标为条件属性C，专家的综合得分作为决策属性D.由专家的得分特点选择合适的粗糙集离散方法将初始数据离散化.

(2)在初始信息系统S=(U,R,V,f)中，对评价对象U，属性值相同的ri,rj∈R的评价能力相同，只需保留一个.根据属性约简的概念，进一步简化信息系统.

(3)利用信息熵概念，从信息观的角度计算各评价指标的客观权重，结合主观权重由公式wi=μβi+(1-μ)αi(0μ1)求得相应评价指标的综合权重wi.

图1井下环境安全水平综合评价流程图

2　应用与实例分析

本文以某地下矿山为例，以验证本文方法的有效性.该地下矿有6个采掘作业区，需要监测的环境指标有CO、H2S、CO2、粉尘浓度、SO2、风速.通过已建成的矿井环境监测系统获得数据,进行离散化处理，并进行属性约简以及利用信息熵的理论计算出各指标的综合权重，最终得到各采场环境安全的水平及排序.

表2是专家对某矿山的6个井下作业区的评价表.C={C1∶CO的值，C2∶H2S的值，C3∶CO2的值，C4∶粉尘浓度,C5∶SO2的值,C6∶风速的值}，决策属性为D={最后总得分}.

(1)实际测量之后转化为标准数据格式如表2所示：

表2　各采场井下环境指标评价初始评价表

离散化标准如表3所示：

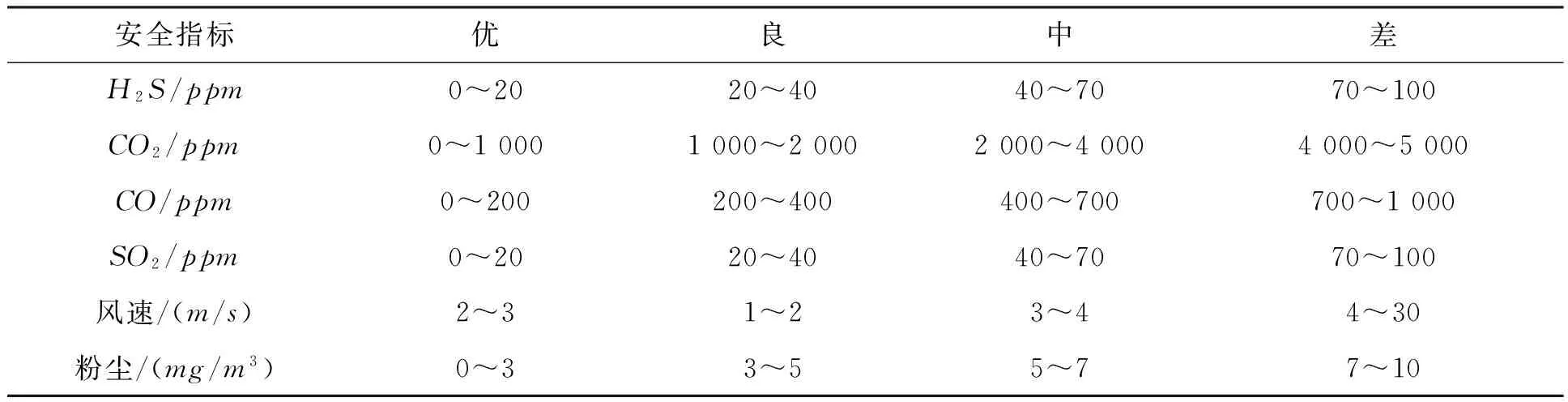
表3　离散化标准

以优、良、中、差的标准，对矿山井下环境安全性水平评价体系的各指标进行评价，结果如表4所示:

表4　各采场井下环境指标评价表

(2)对所有矿山的每个评价指标下的结果按优、良、中、差分别对应1、2、3、4进行进一步离散化处理，从而得到离散化的评判结果，删除属性值相同的重复属性，得到初步简化后的评价情况如表5所示：

表5　各采场井下环境指标评价最终离散化表

(3)计算信息观下各评判指标的权重.由于

U/ind(D)={{u1,u3,u5},{u2,u6},{u4}}；

U/ind(C1)={{u1,u3,u5},{u2,u4},{u6}}；

U/ind(C2)={{u1,u2,u6},{u3,u5},{u4}}；

U/ind(C3)={{u1,u4},{u2,u3},{u5,u6}}；

U/ind(C4)={{u1,u2,u5,u6},{u3},{u4}}；

U/ind(C5)={{u1,u2,u5,u6},{u3,u4}}；

U/ind(C6)={{u1,u5},{u2,u3,u4,u6}}；

U/ind(C)={{u1},{u2},{u3},{u4},{u5},{u6}}；

所以:

H(D)=(1/2)log3+(2/3)；H(D|C1)=1/3；

H(D|C2)=(1/2)log3-(1/3)；H(D|C3)=2/3；

H(D|C4)=2/3；H(D|C5)=1；

H(D|C6)=4/3；

I(C1,D)=H(D)-H(D|{C1})=(1/2)log3+(2/3)-1/3=1.125 815;

I(C2,D)=H(D)-H(D|{C2})=(1/2)log3+(2/3)+1/3=1;

I(C3,D)=H(D)-H(D|{C3})=(1/2)log3+(2/3)-2/3=0.792 481;

I(C4,D)=H(D)-H(D|{C4})=(1/2)log3+(2/3)-2/3=0.792 481;

I(C5,D)=H(D)-H(D|{C5})=(1/2)log3+(2/3)-1=0.459 148;

I(C6，D)=H(D)-H(D|{C6})=(1/2)log3+(2/3)-4/3=0.125 815;

由此得到信息观下的客观权重

α1=0.262，α2=0.233，α3=0.184，α4=0.184，α5=0.108，α6=0.029.

假设决策者根据专家的评价情况得到的主观权重为β1=0.24,β2=0.22，β3=0.20，β4=0.18，β5=0.11，β6=0.03，并经过研究选取权衡因子μ=0.6，则由公式wi=μβi+(1-μ)αi(0≤μ≤1)，得到各评判指标的综合权重W1=0.247，W2=0.224，W3=0.195，W4=0.181，W5=0.109，W6=0.030，故所有指标中最有威胁性的因素是C1，即为CO.

表6　6个作业区井下环境安全性综合评价及排序

得分越高，则安全威胁越大，越危险.故通过综合评价结果可知，3号采场的安全性最高，4号采场的安全性最低，也即4号采场危险系数最大.此时，系统可以做出相应的预警提示，加上之前所得到的客观事实，CO是最重要的安全指标，故我们可以立即对4号矿山的CO安全因素采取安全措施.

3　结语

本文在粗糙集的基础上，结合信息熵等知识的方法，弥补了其它评价方法中主观性和片面性的问题，并且能够有效地减少综合评价问题的计算量，提高评价过程的效率，为客观地对矿山井下环境安全性综合评价工作提供了科学的依据.但由于本实例验证的对象有限，并不能完全适合所有矿山井下环境安全性状况，还有待于更进一步的完善.其进一步的完善可以解决避免现有系统只针对某一对象而设计的单一性，使其可以普遍地应用到不同的环境中.

[1]王玲丁.推动非煤矿山安全生产标准化建设[J].劳动保护,2011(11):13-15.

[2]程德强，李世银，李鹏，等.矿井安全监测监控系统[J].电视技术,2006,2:78-81.

[3]卞长弘，宁培松，王晓滨，等.矿井监测监控系统综述[J].中国煤炭工业,2005(7):62-63.

[4]蒋复量，周科平，李书娜，等.基于粗糙集一神经网络的矿山地质环境影响评价模型及应用[J].中国安全科学学报，2009(8)：126-132.

[5]王佳，于军琪，郭春燕.基于粗糙集一RBF网络的水环境质量评价方法[J].计算机工程与应用，2009(13)：237-239.

[6]周勃，费朝阳，兰信颖，等.基于粗糙集理论的室内环境模糊评价方法[J].暖通空调，2006(4)：21-24.

[7]张改景，王智伟，龙惟定.基于粗糙集的室内环境主观指标的约减[J].建筑热能通风空调，2008(6)：71-73.

[8]王国胤，于洪，杨大春.基于条件信息熵的决策表约简[J].计算机科学，2012，25(7)：759-766.

[9]张文修，吴伟志，粱吉业，等.粗糙集理论与方法[M].北京：科学出版社，2001.

[10]张文修，仇国芳.基于粗糙集的不确定决策[M].北京：清华大学出版社，2005.

[11]王文军，王静.一种高校教师综合能力粗糙集评价方法[J].计算机技术与发展，2012，22(26)：33-37.

[12]肖志军，麦雄发.基于粗糙集理论的教学评价指标权重的确定[J].广西师范学院学报，2010，27(1)：65-69.

[13]刘清.Rough集及Rough推理[M].3版.北京：科学出版社，2005.

[14]KUMARA，KUMARH，PANDEYVN,etal.Gasmonitoringandpowercut-offsystemforundergroundminesIndustrialElectronicsandApplications(ICIEA)[J].IEEEConferenceon,2012(7):463-466.

[15]PAWLAKZ.RoughSets[J].InternationalJournalofInternationlSciences,1982(11)：341-356.

[责任编辑王新奇]

Comprehensive Evaluation of Mine Environmental Safety Factorsbased on Rough Set

SUN Yu-jiea, WANG Wen-qingb

(a.School of Communication and Information Engineering;b. School of Automation, Xi’an University of Posts and Telecommunications, Xi’an 710061,China)

In this paper, the domestic related research in the field of research on rough set of environmental science and engineering and the environment were summarized, and further aiming at the problem of not objective enough that existing in the traditional mine safety monitoring system, based on rough set theory and the method for calculating comprehensive weight of safety factors using information entropy theory, more objective and reasonable comprehensive evaluation were carried out for CO, H2S, dust and other safety factors in underground environment of mine. In order to make more scholars to understand and use the rough set theory and the method, the application of the theory will be promoted in the field of the environment.

rough set; information entropy; comprehensive weight

1008-5564(2016)02-0013-06

2015-12-11

陕西省科技厅项目(2014K05-29)

孙玉洁(1989—)，女，陕西韩城人，西安邮电大学通信与信息工程学院硕士研究生，主要从事现代信号处理及应用研究；

王文庆(1964—)，男，北京人，西安邮电大学自动化学院教授，主要从事智能信息处理研究.

X820.3；TD167

A