基于双树复小波变换的图像清晰度评价算法

兰州大学信息科学与工程学院　邹一帆

基于双树复小波变换的图像清晰度评价算法

兰州大学信息科学与工程学院邹一帆

图像清晰度评价是数字图像处理中的一个重要组成部分，图像清晰度评价算法在图像特征提取、图像质量评估及图像复原等领域中发挥着重要作用。本文算法利用双树复小波变换系数能更精确地表征图像特征的特点，结合FISH和FISHbb算法，提出一种多尺度、多方向的图像清晰度快速评价算法，对图像的清晰度予以数字化的度量。在实验中，以S3算法为标准对比算法改进前后的准确率。最终得出结果：相较于原FISH和FISHbb算法，本算法在保证运算速度的基础上，提高了算法的准确率。

图像清晰度评价；双树复小波变换；FISH；FISHbb

1.引言

尽管人眼可以轻易地区分出不同清晰度的两幅图像，但图像清晰度却并没有一个客观的定义，清晰的图像一般具备更明显的细节和更强对比度的纹理或边缘。尽管如此，图像清晰度评价仍然是数字图像处理中的一个重要组成部分，图像清晰度评价算法在图像特征提取、图像质量评估及图像复原等领域中发挥着重要作用。

目前图像清晰度评价有两种途径：主观评价和客观评价。主观评价方法是以人的视觉效果作为评判准则，由观察者对图像清晰度提出判断；客观评价方法是指用可定量分析的数学模型表达出人对图像的主观感受。主观评价方法需要对图像判读人员进行专门的训练，评价过程费时耗力，经济性差。而客观评价方法从理论出发，快速稳定，能给出定量数据，但它忽略了人的视觉特性，有时与人的主观感受不一致。因此开发出与人对图像的主观感受相一致的客观质量评价方法显得尤为重要［1］。

本文提出的是一种基于双树复小波变换的图像清晰度快速客观评价算法，该算法是在Phong V. Vu提出的FISH（Fast Image Sharpness，FISH）和FISHbb（Fast Image Sharpness Block Based，FISHbb）算法上进行改进而得来的［2］。双树复小波变换系数能更精确地表征图像特征的特点，相较于FISH和FISHbb算法，本算法在保证运算速度的基础上一定程度地提高了图像清晰度估计的准确率。

2.现有的图像清晰度评价函数

现有的图像清晰度算法大致可分为三类［3］：（1）基于图像边缘处理的算法，该类算法主要着重于图像的边缘检测；（2）基于像素的算法，该类算法主要着重于图像空间域的特性而不涉及图像的边缘检测；（3）基于数学变换的算法，该类算法主要着重于图像的频域特性。

1）基于图像边缘处理的算法

分析图像的边缘是图像清晰度算法中一项常用的技术，因为具有更强对比度边缘的图像会使人感觉更清晰。

Marziliano等人提出了一种图像清晰度算法，在该算法中他们首先识别图像垂直方向上的边缘，然后通过检测这些边缘的宽度来计算图像清晰度［4］。在Ong等人提出的算法中同时检测图像边缘和图像梯度方向，然后图像的清晰度取决于图像梯度方向和反方向的边缘宽度的平均值［5］。

2）基于像素的算法

也有很多图像清晰度算法利用图像在空间域的特性而不涉及与图像边缘相关的假设。

Wee等人认为一幅图像的特征值包含这幅图像最大方差方面的信息，从而用主导特征值来估计清晰度。他们首先计算图像的协方差矩阵的特征值，然后将前几个特征值作为图像的清晰度指标［6］。用类似的方法，Zhu和Milanfar根据图像的梯度矩阵的奇异值分解来估计图像清晰度。他们的观点是，由于奇异值反映图像沿主导方向和垂直方向的梯度强度，所以奇异值会敏感于图像清晰度。因此，局部图像梯度矩阵的奇异值可以用来估计图像的清晰度［7］。

3）基于数学变换的算法

另一些算法利用图像的谱域变换如离散余弦变换或散傅里叶变换来估计图像清晰度。

Marichal等人将图像分解为8×8的小块，然后通过计算这些小块的非零离散小波变换系数来计算图像清晰度［8］。同样利用离散小波变换，Caviedes和Gurbuz提出一种基于块的算法，利用小波系数的峰值来计算图像清晰度。该算法由每个小块的边缘轮廓的平均清晰度值得出整体图像的清晰度［9］。

3.双树复小波变换

传统的二维离散小波变换它的方向选择性是十分有限的，在每一个尺度空间中只能被分解成三个方向的细节信息：即水平方向、垂直方向和斜方向，然而在某些特定的情况下，需要对图像的某些方向上的纹理或边界进行增强，此时传统的二维小波变换由于自身缺乏方向选择性就无法满足分析的需要。

为了克服二维离散小波方向选择性差的缺点，1998年英国剑桥大学的Kingsbury等人提出了双树复小波变换（The Dual-Tree Complex Wavelet Transform，DTCWT），它是在复小波变换的基础上发展起来的，不仅具有传统小波变换的优良特性还能够更多地描述图像的方向性信息。双树复小波变换是通过实数小波变换来实现复数小波变换，它将复小波的实部和虚部分离开，通过两组并行的实数滤波器组来获取实部和虚部的小波变换系数［10］。

一维双树复小波变换的实现结构如图1所示。对二维的图像，可通过分离的滤波器内积进行变换。

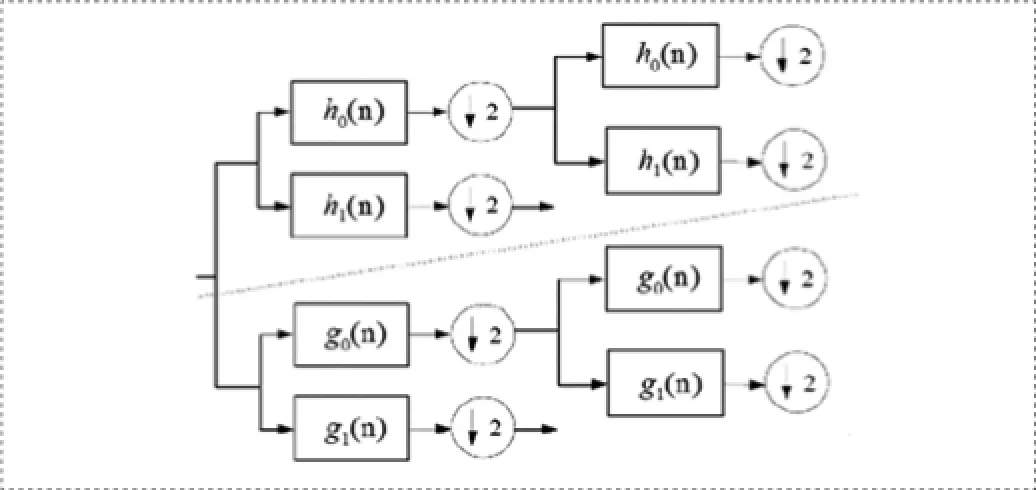
图1　双树复小波变换的实现结构

双树复小波变换不仅保持了传统的实小波变换多分辨率特性和时频局部化的分析能力，而且具有更好的方向选择性、平移不变性、有限的数据冗余和高效的计算效率。

4.基于双树复小波变换图像清晰度评价算法

Phong V.Vu提出了一种基于小波变换的图像清晰度评价快速算法FISH。该算法首先将输入图像经过一次三层离散小波分解，然后对离散小波的各子带进行对数能量计算，最后将这些对数能量进行加权平均计算得到一个图像清晰度值。在此基础上Phong V. Vu又提出了基于图像分割的FISHbb算法，FISHbb通过计算分割后的图像FISH值得到最终整幅图像的清晰度值。

本文的算法是双树复小波变换在FISH和FISHbb算法基础上的改进。

对于一幅输入灰度图像，DTCWT FISH算法共含三个个步骤：

1）步骤一：双树离散小波变换计算：通过Cohen Daubechies Fauraue 9/7滤波器对输入图像进行三层双树复小波变换，得到S15n，S45n，S75n，S-15n，S-45n，S-75n分别代表DTCWT第n层的±15°，±45°，±75°子带的小波系数。

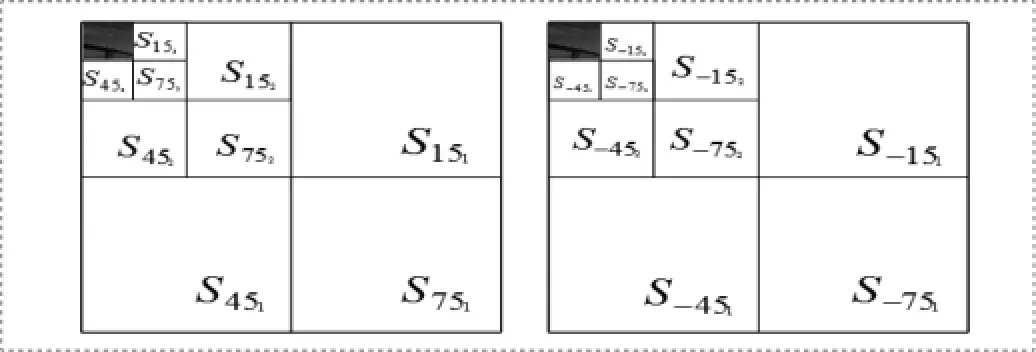
图2　三层双树复小波变换

2）步骤二：计算每层离散小波变换的对数能量：由于较清晰的图像包含更多的高频分量。为利用这一结论，对每一层双树复小波变换子带进行对数能量计算，算法如下：

其中XY代表±15°，±45°或±75°，n代表双树复小波变换层数，San代表双树复小波变换第n层的±15°，±45°，±75°子带的小波系数。Nn代表第n层小波系数个数，加1的目的是避免结果为负数。

然后计算每层双树复小波变换的总对数能量，算法如下：

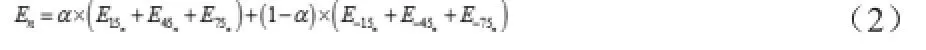
其中a为比例系数，经实验得到最佳结果为0.7。

3）步骤三：计算图像清晰度值：将三层双树复小波变换对数能量结合起来得到图像的总清晰度值，算法如下：

其中，FISH代表图像总清晰度值，数值越大代表图像越清晰。n代表双树复小波变换层数，，其中较低的层数具有较高的权重。

FISH算法是针对整幅输入图像清晰度的算法，相对应的双树复小波变换也可用于基于图像分割的FISHbb算法，FISHbb通过计算分割后的图像FISH值得到最终整幅图像的清晰度值。

在FISHbb算法中将图像分割成多幅16×16的小块图像，在分割过程中相邻的两幅图像间有50%的重叠，即横向相邻两幅图像中有8列重叠，纵向相邻的两幅图像中有8行重叠，如图2。然后将这些小块图像进行三层离散小波变换，每层的子带分别是8×8，4×4，和2×2的小块，再将之前的FISH算法应用于小块图像得到其图像清晰度值。最后取这些值中最大的1%部分进行计算得出整幅图像的清晰度值，算法如下：

其中T代表最大的1%FISH值的个数，FISHi中的i=1，2，3...，T代表最大的1%FISH值所代表的小块图像。取1%的原因是图像的清晰度很大程度上取决于图像最清晰部分的清晰度。

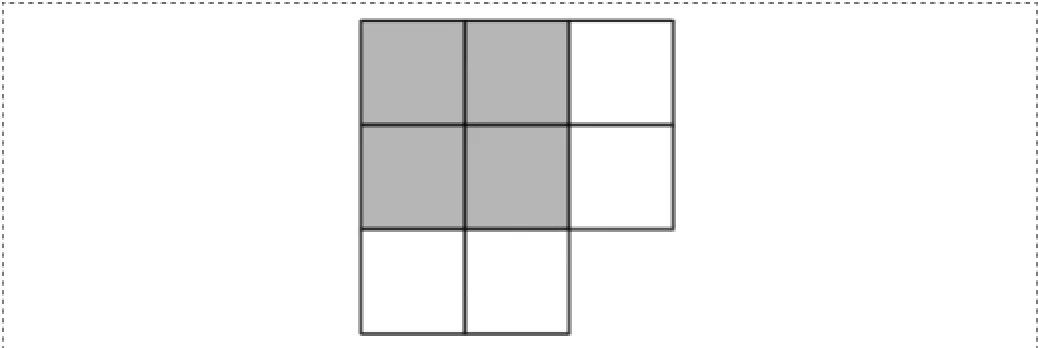
图3

FISHbb中对图像的分割示例，其中相邻两幅小块图像中有50%的部分重叠，图中每小格代表4×4小块图像。

5.实验结果对比

S3算法是C.T. Vu提出的一种图像清晰度算法［3］，该算法同时利用图像的光谱和空间特性，C. T. Vu计算图像幅度谱斜率和总空间变化的斜率。S3算法是一种相对精确的图像清晰度评估算法，该算法同时利用图像的光谱和空间特性，它并不单纯依赖于对于图像边缘等特性，从而提高了其对于不同图像的清晰度评估的准确率。因此本文选取S3算法为标准对比快速算法的准确率。

在实验中选取共49幅灰度图像为实验对象，分别用DWT FISH，DWT FISHbb，DTCWT FISH，DTCWT FISHbb（DWT FISH和DWT FISHbb为Phong V. Vu提出的原算法，DTCWT FISH和DTCWT FISHbb为本文提出的改进算法）和S3共5种算法对这些图像清晰度进行评估。

以S3算法为标准对比，DWT FISH，DWT FISHbb，DTCWT FISH和DTCWT FISHbb算法的图像清晰度评价准确率如表1所示：

表1　以S3算法为标准，改进前后算法图像清晰度评价准确率

由此结果可以看出：相较于基于DWT的原FISH和FISHbb算法，改进后算法图像清晰度评价的准确率分别提高了4.09%和8.17%。

各算法平均每幅图像处理时间如表2：

表2　算法平均处理时间比对

DWT FISH，DWT FISHbb，DTCWT FISH和DTCWT FISHbb算法的运算速率要远快于S3算法。而DTCWT FISH和DTCWT FISHbb算法相较于DWT FISH，DWT FISHbb算法在提高了运算准确率的基础上，虽然运算速率有所降低，但相较于S3算法仍然是运算速率很快的快速算法。

6.结论

本文的算法是基于双树复小波变换在FISH算法和FISHbb算法基础上的改进算法，算法首先将输入图像经过一次三层双树复小波变换，然后对离散小波的各子带进行对数能量计算，最后将这些对数能量进行加权求和计算得到一个图像清晰度值。

该算法是一种图像清晰度评价快速算法，延续了FISH和FISHbb的快速算法思路，相对于普通图像清晰度评价算法，在运算速率上有很大的提升，而通过利用双树复小波变换的对原算法进行改进，相较于之前的FISH和FISHbb算法在准确率上又有一定的提高。

［1］李祚林，李晓辉，马灵玲，胡玥，唐伶俐.面向无参考图像的清晰度评价方法研究［J］.遥感技术与应用：第26卷2期，2011年4月：239-246.

［2］Phong V.Vu and Damon M. Chandler，” A Fast Wavelet-Based Algorithm for Global and Local Image Sharpness Estimation，” IEEE Signal Processing Letters， 2012，19（7）：423-426

［3］C.T.Vu，T.D.Phan，and D.M.Chandler，“S3： A spectral and spatial measure of local perceived sharpness in natural images，” IEEE Transactions on Image Processing， vol. 21， no. 3， Mar 2012， pp. 87 –99.

［4］P. Marziliano，F. Dufaux，S.Winkler， T. Ebrahimi， and G. Sa，“A no-reference perceptual blur metric，” in IEEE 2002 International Conference on Image Processing， 2002， pp. 57–60.

［5］E.Ong，W.Lin，Z.Lu，X.Yang，S.Yao，F.Pan，L.Jiang， and F. Moschetti， “A no-reference quality metric for measuring image blur，” in Seventh International Symposium on Signal Processing and Its Applications， 2003， vol. 1， pp. 469–472.

［6］C. Y. Wee and R. Paramesran， “Image sharpness measure using eigenvalues，” in 9th International Conference on Signal Processing，ICSP.， 2008， pp. 840 –843.

［7］X.Zhu and P. Milanfar， “A no-reference sharpness metric sensitive to blur and noise，” in 1st International Workshop on Quality of Multimedia Experience （QoMEX）， 2009.

［8］X.Marichal，W.Y.Ma，and H.J.Zhang，“Blur determination in the compressed domain using dct information，”in IEEE International Conference on Image Processing， 1999， vol. 2， pp.386390.

［9］J.Caviedes and S.Gurbuz，“No-reference sharpness metric based on local edge kurtosis，”in IEEE International Conference Image Processing， 2002， vol.3，pp. III–53–III–56.

［10］石宏理，胡波.双树复小波变换及其应用综述［J］.信息与电子工程：第5卷3期，2007年6月：229-234.

邹一帆（1990－），男，山西太原人，硕士，现就读于兰州大学信息科学与工程学院，研究方向：电子与通信工程。