混凝土框架二阶效应中美规范设计应用对比分析
王国敏(中交第二航务工程勘察设计院有限公司,湖北 武汉 430071)
混凝土框架二阶效应中美规范设计应用对比分析
王国敏
(中交第二航务工程勘察设计院有限公司,湖北 武汉 430071)
框架结构因其结构简单、受力明确、施工便利,在工程建设中得到广泛的应用。同时,由于框架结构相对侧移刚度较弱,其二阶效应较为明显。本文结合海外工程设计经验,通过对中美规范有关框架结构二阶效应内容的对比研究分析,提供有关应用结论和建议,供设计人员参考。
二阶效应;层间位移;挠曲变形;刚度
引 言
作用在结构上的重力或构件中的轴压力,在产生了层间位移的结构和挠曲变形的构件中引起的附加内力和附加变形,称为结构的二阶效应。二阶效应包括层间位移引起的弯矩增大的重力二阶效应(称为P-Δ效应)和受压构件挠曲变形引起弯矩增大的挠曲效应(称为P-δ效应)。二阶效应计算可采用有限元方法及简化计算法。本文以中美规范有关框架结构二阶效应的相关内容为主,结合海外工程设计经验,对比研究二阶效应的简化计算方法及相关规定,提供有关应用结论和建议。
1 中美规范简化设计方法及相关规定
《混凝土结构设计规范》(GB50010)(以下简称“GB50010”)均按有侧移框架考虑,分别给出P-Δ、P-δ效应计算方法;《Building Code Requirements for Structural Concrete(ACI318)and Commentary》(以下简称“ACI318”)则应判断框架有无侧移,再分别计算其二阶效应。
1.1二阶效应简化设计方法
1)中国规范
GB50010给出的P-Δ效应的增大系数法计算公式如下:

其中:Δ=ηsΔ1;ηs=1/(1-∑Nj/DH0)。
式中符号含义见GB50010。
《高层建筑混凝土结构技术规程》(JGJ3-2010)(以下简称“JGJ3-2010”)给出的P-Δ效应计算公式与公式(1)相同。
GB50010给出的框架结构P-δ效应的增大系数法计算公式如下:

其中:Cm=0.7+0.3M1/M2;ηns=1+(lc/h)2×ζc/ [1 300h0(M2/N+ea)];ζc=0.5fcA/N,当Cmηm小于1.0时,取1.0。
式中符号含义见GB50010。
2)美国规范
美标ACI318给出的无侧移框架二阶效应(P-δ效应)简化计算公式如下:

其中δ=Cm/(1-Pu/0.75Pc)≥1.0。
式中:
Mc为考虑二阶效应的增大弯矩;
M2为受压构件乘了系数的端力矩较大值,如果横向荷载作用在支点之间,M2取构件上的最大值,M2恒为正且不小于M2,min,M2,min=Pu(0.6+0.3h),h为截面高;
Pc为临界荷载,Pc=π2EI/(klu)2,其中 EI= (0.2Eclg+Eslse)/(1+βdns)或EI=0.4Eclg/(1+βdns),为了简化计算,可以假定βdns=0.6,EI=0.25EcIg;
Pu为乘了系数的轴向荷载,Pu≤φPu,φ=0.75,Pu为横截面标称强度;
其他符号含义见ACI318。
美标 ACI318-1给出的有侧移框架二阶效应简化计算公式如下:
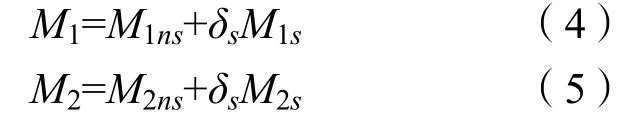
式中:
M1为受压构件较小的乘系数的端弯矩,M1<1.4(M1ns+M1s);
M2为受压构件较大的乘系数的端弯矩,M2<1.4(M2ns+M2s);
M1ns、M2ns为不引起结构侧移的荷载作用下,用一阶弹性分析计算出的乘了系数的柱端弯矩;
M1s、M2s为引起结构侧移的荷载作用下,用一阶弹性分析计算出的乘了系数的柱端弯矩;
δs为有侧移框架的弯矩增大系数,按下式计算:

如按式(6)计算得出的δs大于1.5,则应通过二阶弹性分析按下式计算:
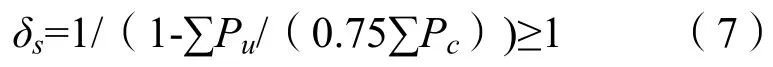
其中,∑Pu为楼层中所有乘了系数的竖向荷载之和,Pc见式(3)。
3)比较分析
中国规范不区分框架有无侧移,分别计算P-Δ、P-δ效应。
美国规范要求按有侧移与无侧移分别计算P-Δ、P-δ效应。计算无侧移框架的二阶效应公式(3)中,按P-Δ效应的直线弯矩图考虑,忽略P-δ效应;一般情况下,构件挠曲变形的曲线弯矩图所导致的侧向位移比按P-Δ效应的直线弯矩图大15%左右,如考虑该影响,则公式(6)中的“Q”可乘1.15;计算有侧移框架二阶效应弯矩增大系数 δs时,如δs>1.5,则应按公式(7)进行楼层稳定性验算,并要求受压构件、约束梁或其他结构中包括二阶效应在内的总弯矩不得超过一阶效应产生的弯矩的 1.4倍。
计算P-δ效应时,中国规范规定构件的计算长度可近视取偏心受压构件相应主轴方向上下支撑点之间的距离,一般取层高;美国规范规定的受压构件的无支撑长度,可取楼板、横梁或其它在对应方向提供侧向支撑的构件之间的净距离。当框架梁截面高度较大时,两者计算结果偏差较大。
刚度取值,在“极限状态”下,结构构件可能开裂而导致刚度退化,结构计算中,结构内各类构件的受力及变形状态应与此相呼应。故考虑刚度退化的影响,能较合理的反映结构或构件在该极限状态下的内力分布及变形规律,包含二阶效应。
中国规范规定的位移限值均为弹性位移(见《建筑抗震设计规范》(GB50011)),且考虑二阶效应后的位移限值不变。为使考虑二阶效应后的位移值(含一阶效应下的弹性位移)能与规范规定的弹性位移限值匹配,在考虑二阶效应的结构位移增大系数计算时,不考虑刚度折减,产生楼层侧移的荷载取标准值。如计算的位移较大时,《建筑抗震设计规范》(GB50011)建议“宜适当考虑构件开裂时的刚度退化,如取0.85EcIo”。
考虑二阶效应的结构构件内力增大系数计算时,中国规范均要求考虑结构刚度的折减。由于各类构件沿长度方向各截面所受弯矩的大小不同,非弹性性能的发展特征也各有不同,导致构件弯曲刚度降低规律较为复杂。为便于工程应用,通过考虑非线性性能的结构分析,并参考试验结果,按结构非弹性侧向位移相等的原则,给出按构件类型的统一当量刚度的折减系数,见GB50010;为简化计算并适当提高结构构件承载力的安全储备,JGJ3-2010提出刚度折减系数可近视取0.5。
ACI318规定:“弹性二阶分析在考虑确定截面性质时,应将轴向荷载的影响、构件长度方向上的开裂区以及荷载特性持续影响列入考虑范围”。用作强度设计分析中,所采用的刚度 EI要能体现构件临近破坏时的刚度,在预计接近极限荷载下的侧向位移的二阶分析中尤为重要。故ACI318在一阶结构位移计算、考虑二阶效应的结构构件内力增大系数计算时,EI均采用折减后的刚度。
1.2整体稳定判断准则
1)中国规范
JGJ3-2010规定框架结构整体稳定性应符合下式要求:
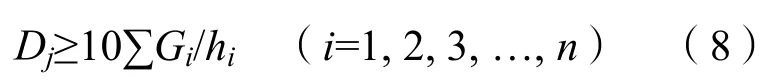
式中符号含义见JGJ3-2010。
《建筑抗震设计规范》(GB50011)(以下简称“GB50011”)规定:当结构在地震作用下的重力附加弯矩大于初始弯矩的10%时,应计入重力二阶效应的影响,如下式所示:
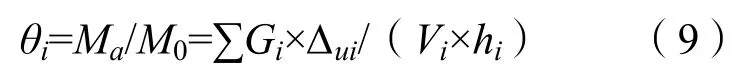
式中符号含义见GB50011。
经对公式(9)转换,可得以下公式:
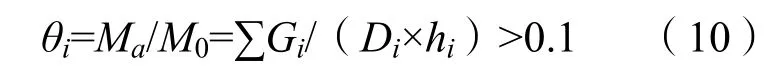
即:
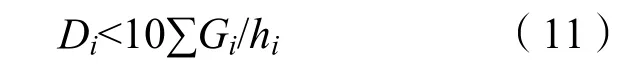
公式(11)是考虑重力二阶效影响的下限,结合JGJ3-2010规定,当Di≥10∑Gi/hi时,可不考虑二阶效应带来的整体稳定问题。鉴于高层建筑特点,JGJ3-2010在框架结构整体稳定性上从严规定Di应大于或等于10∑Gi/hi。
2)美国规范
受压构件、约束梁或其他结构中包括二阶效应在内的总弯矩不得超过一阶效应产生的弯矩的 1.4倍。
计算有侧移框架二阶效应弯矩增大系数δs时,如δs>1.5,则应按公式(7)进行楼层稳定性验算。
3)比较分析
在考虑弹性刚度折减50%的情况下,重力P-Δ效应控制在20%之内时,结构的稳定具有适宜的安全储备,JGJ3-2010以此(见公式8)作为整体稳定性的最低要求。
ACI318通过二级弹性分析或按公式(7)进行楼层稳定效应验算,此时,δs是在∑Pu/∑Pc的基础上作为整个楼层的平均值来计算,以此反映楼层中所有柱参与抵抗侧移的柱之间的相互影响。
中美规范在重力P-Δ效应的计算公式中,均未考虑结构存在的明显扭转位移的情况。故当结构侧向位移中存在明显的扭转位移时,以上计算方法可能低估离扭转中心较远的柱的重力P-Δ效应。在此情况下需要采用三维二阶分析。
1.3忽略二阶效应的准则
1)中国规范
忽略P-δ效应的准则:GB50010规定,弯矩作用平面内截面对称的偏心受压构件,当同一主轴方向的杆端弯矩比M1/M2不大于0.9,且轴压比不大于0.9时,若构件的长细比满足以下要求时,可不考虑轴向压力在该方向的P-δ效应:
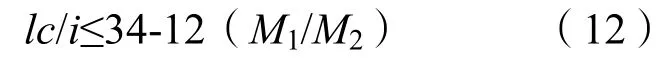
式中:i为偏心方向的截面回转半径。
忽略P-Δ效应的准则:当高层建筑框架结构满足下列规定时,弹性计算分析时可不考虑重力二阶效应的不利影响。
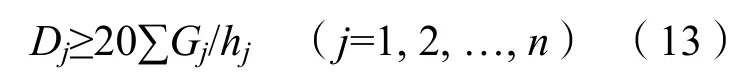
2)美国规范
忽略P-δ效应的准则:在满足以下条件时的受压构件应允许忽略二阶效应:
有侧移框架:
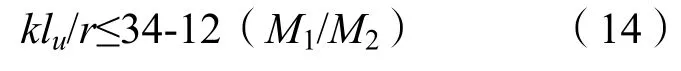
无侧移框架:

其中:M1/M2在柱以单曲弯曲时取正值,以双曲弯曲弯曲时取负值;r为构件截面的回转半径,对矩形截面,r可取稳定方向截面尺寸的0.3倍,对园形截面,r可取园形截面直径的0.25倍。
忽略P-Δ效应的准则:P-Δ效应只发生在有侧移的结构中,如结构中某柱、某楼层满足无侧移框架的要求,则可忽略P-Δ效应。
如结构中某柱的端弯矩因二阶效应而增大的幅度未超过一阶弯矩的5%,则该柱应允许假定为无侧移。
如结构中某楼层由下式计算得出的 Q值小于或等于0.05,则该楼层应允许假定为无侧移:
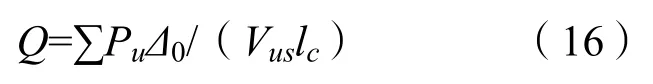
式中:
∑Pu为所计算楼层中乘了系数的竖向荷载之和;
Vus为所计算楼层中乘了系数的楼层水平剪力之和;
Δ0为该楼层上下之间由 Vus产生的一阶相对侧向位移;
lc为受压构件长度,取框架结构中节点中心之间的的长度。
为确定结构使用性能,在挠度、振动和建筑周期的分析中,需要在各种使用荷载(不乘系数)下完成,结构构件在使用荷载分析中的惯性矩要体现所考查的不同使用荷载水平下的开裂程度,故美国规范规定在计算Δ0中所采用的EI均采用折减后的刚度。若由一阶使用荷载,在考虑刚度折减情况下,计算得到框架层间位移,则ACI318规定可取用重力荷载之和的1.2倍、使用荷载(不乘系数)产生的楼层剪力以及 1.43倍的一阶使用荷载计算得到框架层间位移,由上式计算Q值。
3)比较分析
GB50010只给出定性的判断标准(当结构的二阶效应可能使作用效应显著增大时,在结构分析中应考虑二阶效应的不利影响),未提供定量的判断方法。GB50011、JGJ3-2010在判断是否需考虑二阶效应问题上,表达方式不同,但实质规定一致。应用以上规范在判断是否需考虑二阶效应的不利影响时,楼层剪力应取标准值,弹性层间位移应取对应多遇地震作用标准值或水平力标准值产生的最大层间位移;结构位移增大系数计算时,不考虑结构刚度的折减;内力增大系数计算时,考虑结构刚度的折减,对梁,取0.4,对柱,取0.6,为简化计算,折减系数可近视取0.5;根据JGJ3-2010规定第i重力荷载设计值Gi取1.2倍永久荷载标准值与1.4倍楼面可变荷载标准值的组合,考虑到不同的荷载组合对应的二阶效应不同,工业建筑(如港口生产建筑)应采用对应荷载组合项中的柱底压力设计值。
JGJ3-2010按结构的弹性分析的二阶效应对结构位移的增量控制在5%左右,考虑实际刚度折减50%时,引起结构侧移的荷载产生的柱端弯矩增量控制在 10%以内,作为忽略 P-Δ效应的准则;ACIA318-11按二阶效应(考虑刚度折减)计算得出的侧向荷载弯矩增量不超过5%作为忽略P-Δ效应的准则。两者比较,美国规范严于中国规范。
2 计算对比
算例:图1为两层无围护的混凝土框架结构转接塔,混凝土强度等级C35,fc=16.7 MPa,Ec=3.0×104MPa,设备活荷载考虑同时发生,不计地震作用,计算柱2的二阶效应。
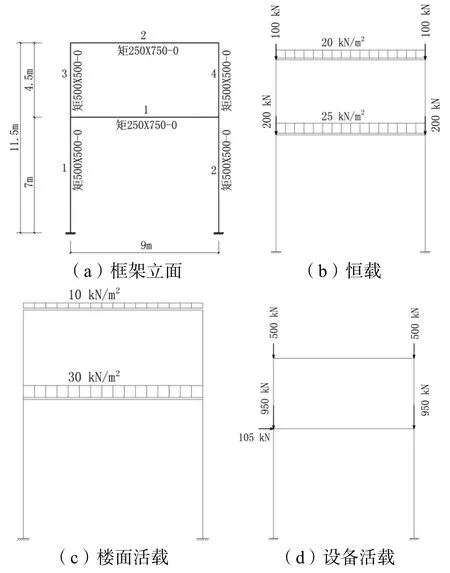
图1 算例示意
2.1依据GB50010计算二阶效应
1)2柱柱底内力及内力组合如表1、表2。
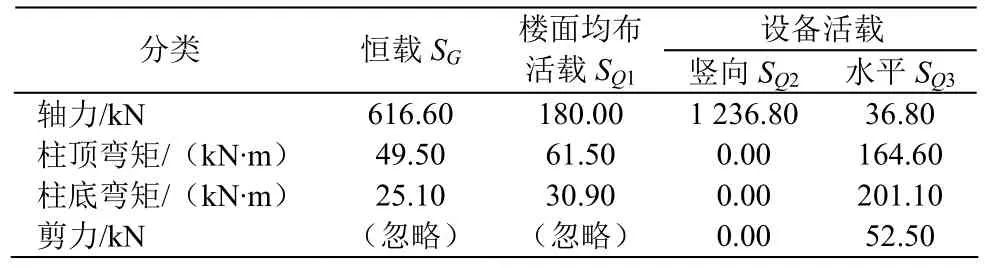
表1 柱底内力
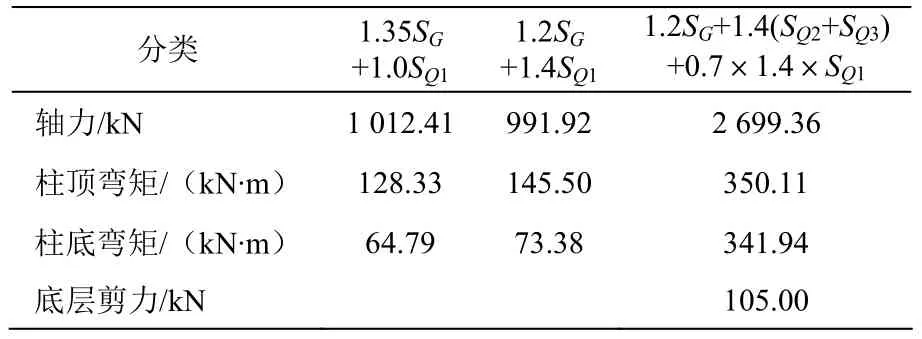
表2 柱底内力组合
2)P-Δ效应计算
当计算弯矩增大系数时,对构件的弹性抗弯刚度ECI乘以折减系数:对梁,取0.4,对柱,取0.6,经计算Δ=21.5 mm,考虑二阶效应后,2柱上、下端弯矩M计算结果见表3。
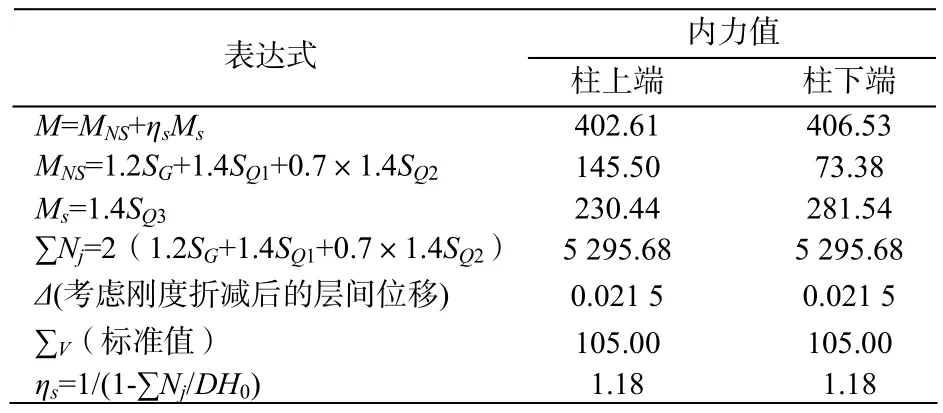
表3 P-Δ效应
当计算位移增大系数时,不对刚度进行折减,经计算Δ=21.5 mm,考虑二阶效应后,2柱上端位移计算结果见表4。

表4 P-Δ效应(位移)
未考虑二阶效应前,楼层(二层)层间位移角:1/588,考虑二阶效应后,楼层(二层)层间位移角:1/538。
3)P-δ效应计算
M1/M2=402.61/406.53=0.99>0.9;
lc/i=7 000/(0.289×500)=48.44;
34-12(M1/M2)=34+12×0.99=45.88;
lc/i>34-12(M1/M2)。
故,应考虑P-δ效应,计算结果见表5。

表5 P-δ效应计算结果
2.2依据ACI318-11计算二阶效应
1)2柱柱底内力及内力组合如表6、表7。
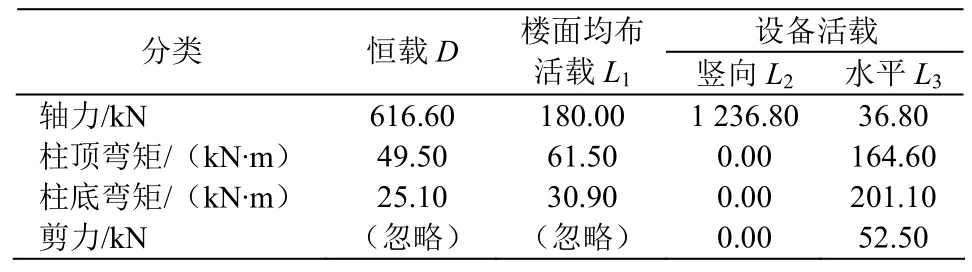
表6 柱底内力
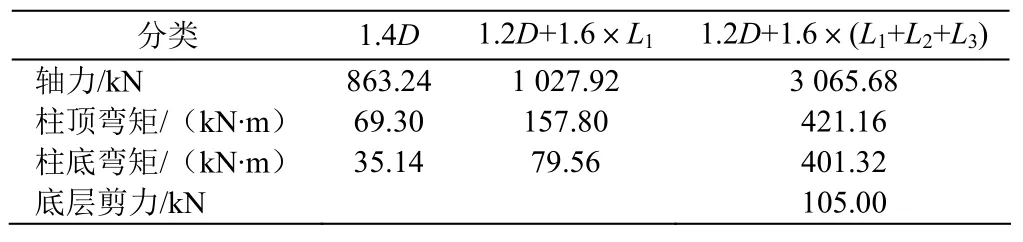
表7 柱底内力组合
2)框架侧移判断
计算楼层侧移时,对构件的弹性抗弯刚度ECI乘以折减系数:对梁,取 0.35,对柱,取 0.7,经计算Δ=19.9 mm,Δ0=1.6Δ=31.36。Q计算结果见表8。

表8 Q计算结果
Q=0.16>0.05,为有侧移框架,按公式(4)、公式(5)计算二阶效应。考虑二阶效应后,2柱上、下端弯矩M计算结果见9。

表9 二阶效应计算结果
2.3二阶效应计算结果比较
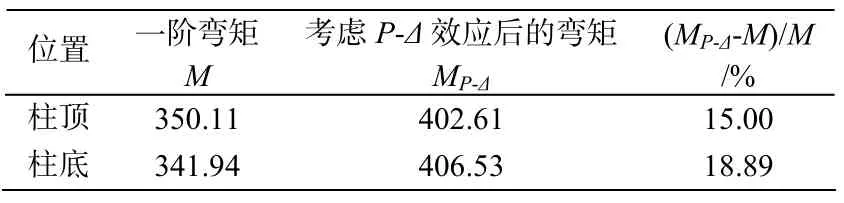
表10 中国规范
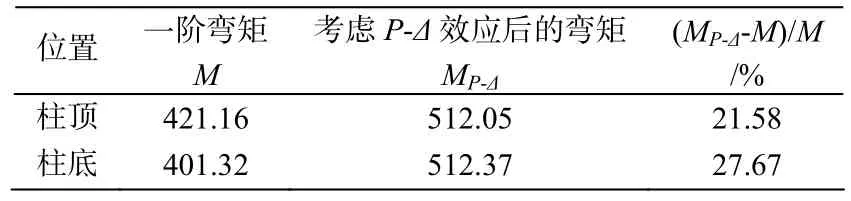
表11 美国规范
3 结 论
1)结合以上算例,P-Δ效应只会增大由引起结构侧移荷载(如:弯矩、偏心压力或水平力)或作用所产生的构件内力,而不增大由不引起结构侧移的荷载(如:较为对称的结构上作用的对称竖向荷载)所产生的构件内力。受压构件中由轴向压力在产生挠曲变形的杆件内引起的曲率和弯矩的增量,当柱反弯点位于柱高中部时,柱中任一截面在考虑P-δ效应后的弯矩不会超过最大柱端一阶弯矩,P-δ效应不会对柱截面受压承载能力产生不利影响,此时,柱截面设计中没必要考虑P-δ效应;当反弯点不在柱高中范围时(即单曲率弯曲),P-δ效应增大后的柱中部弯矩有可能超过柱端控制截面的弯矩,此时,柱截面设计中就应考虑P-δ效应。
2)中国规范不区分框架有无侧移,分别计算P-Δ、P-δ效应;美国规范要求按有侧移与无侧移分别计算 P-Δ、P-δ效应,在有侧移的框架中,美国规范忽略构件挠曲变形引起的曲率和弯矩的增量。
3)中美规范在判断是否要考虑 P-Δ效应的公式相同,但因中国规范采用的是未折减的刚度、而美国规范采用的是折减后的刚度,故美国规范规定严于中国规范。
4)当需要控制结构楼层侧向位移时,楼层侧向位移量应考虑因二阶效应增大的侧移量。
5)中、美规范简化计算重力二阶效应的基本公式相同,构件的弹性抗弯刚度ECI折减幅度相近;美国规范活载分项系数较中国规范大,乘系数后的重力荷载较中国规范大,考虑P-Δ效应后,按美国规范计算的P-Δ效应后的侧移荷载产生的弯矩增量略大于中国规范,总弯矩增量亦大于中国规范。
6)中国规范(GB50010)未对弯矩增大系数进行限制,JGJ3-2010对框架结构在整体稳定性上要求符合公式(8),即考虑 P-Δ效应的弯矩增大系数ηs≤1.25;美国规范规定侧移框架二阶效应弯矩增大系数 δs>1.5时,应按公式(7)进行整体稳定验算,且受压构件、约束梁或其他结构中包括二阶效应在内的总弯矩不得超过一阶效应产生的弯矩的1.4倍。故在高层建筑稳定性要求方面,中国规范较美国规范严。
7)如本文算例所示,当结构形式、截面及材料一定时,结构的重力二阶效应增大系数只与重力荷载相关,当重力荷载增大时,结构的重力二阶效增大系数亦增大。
8)中美规范在重力 P-Δ效应的计算公式中,均未考虑结构存在的明显扭转位移的情况。当结构侧向位移中存在明显的扭转位移时,以上计算方法可能低估离扭转中心较远的柱的重力P-Δ效应。在此情况下需采取措施减少结构的扭转位移并采用三维二阶分析。
9)在“极限状态”下,结构构件可能开裂而导致刚度退化。为此,结构计算中,结构内各类构件的受力及变形状态应与此呼应。故建议中国规范在计算结构位移,包括计算结构二阶位移时,统一采用折减后的构件刚度。
10)对高层建筑、受水平荷载及竖向荷载较大的工业建筑(如港口工程转运站建筑),应重视并合理考虑二阶效应。
[1]GB50011-2010 建筑抗震设计规范[S].
[2]JGJ3-2010 高层建筑混凝土结构技术规程[S].
[3]GB50010-2010 混凝土结构设计规范[S].
[4]ACI318 Building Code Requirements for Structural Concrete(ACI318)and Commentary[S].
Comparative Analysis of Design Application of Second-order Effect of Concrete Frame Stipulated in Chinese and American Standards
Wang Guomin
(CCCC Second Harbor Consultants Co.,Ltd.,Wuhan Hubei 430071,China)
The framing structure has been widely used in the construction due to its simple structure,obvious stress and construction convenience.In addition,the frame structure is characterized with weaker stiffness of relative lateral displacement and more obvious second-order effect.Based on overseas engineering design experiences,by comparing,analyzing and studying the second-order effect of framing structure stipulated in Chinese and American standards,relevant conclusions and suggestions are put forward as a reference for the design.
second-order effect; interlayer displacement; flexural deformation; stiffness
TU375.4
A
1004-9592(2016)04-0068-06
10.16403/j.cnki.ggjs20160417
2015-11-18
王国敏(1962-),女,高级工程师,主要从事结构设计工作。

