索托节点的数值模拟方法研究

杨维国, 王萌, 王亚, 阮志勇

(北京交通大学 土木建筑工程学院，北京 100044)



索托节点的数值模拟方法研究

杨维国, 王萌, 王亚, 阮志勇

(北京交通大学 土木建筑工程学院，北京 100044)

为了更加准确地模拟索托结构中的索托节点，本文利用ANSYS软件进行整体桁架的模拟并进行相关的有限元分析，提出一种新的索托节点数值模拟方法，即不变刚度短梁法，并与其他3种数值模拟方法(自由度耦合方法、自由度耦合加变刚度弹簧单元方法、点-点接触方法)进行分析对比。结果表明：4种方法对桁架结构挠度和构件内力引起的差别并不明显，结果基本吻合，内力走势一致。由于自由度耦合加变刚度弹簧单元方法已得到验证，故说明本文提出的不变刚度短梁法是合理可行的；自由度耦合加变刚度弹簧单元方法和不变刚度短梁法能更好地模拟索托节点处的摩擦力行为，而且这两种方法理论明确且计算简单方便，是相对较好的索托节点数值模拟方法。

索托节点；数值模拟；不变刚度短梁法；自由度耦合；变刚度弹簧；点-点接触；摩擦力

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20160623.0827.006.html

索托结构是一种新型大跨空间结构形式[1-2]，是在总结斜拉结构和悬索结构优缺点的基础上提出的全新结构形式。索托结构是指索体从结构的底部穿过，将结构托起，索托结构外形类似于斜拉结构，但受力模式却完全不同。索托结构中索为结构提供竖向弹性支撑，同时也有效地减小了索对主体结构的有害水平分力，使结构能够实现更大的跨度。

索托结构设计中如何对索托节点进行准确模拟是一个关键问题。对索托结构进行理论计算需确定索托节点接触问题的种类，运用合适的求解方法来满足工程精度及收敛性要求。考虑到索托节点计算的非线性及对计算工作量的要求，需要在索托结构体系的计算中对索托节点采用简化处理的方法。既不能违背索托结构的基本性能，又要达到简化计算的目的[3]。索托结构中，拉索可以在索托节点处自由地滑动使两侧索力趋于平衡，但摩擦力是不可避免的因素，所以索托节点两侧索力不相等。根据索托预应力节点足尺试验可知[3]，拉索摩擦损失随张拉力的增大而增大，损失值约为张拉力的1%～5%，如何模拟索托节点处的摩擦力是准确模拟索托节点受力行为最主要的问题。

在现有的3种模拟方法(自由度耦合方法[4]、自由度耦合加变刚度弹簧单元方法[5]、点-点接触方法[3])基础上，提出了不变刚度短梁法。以桁架结构为例，对4种方法进行桁架结构挠度、构件内力与索托节点摩擦力行为的对比和评价。最后确定模拟索托节点最准确的方法。

1　模型参数与荷载条件

1.1模型参数

本文以北京芦城体校曲棍球馆索托结构为例进行计算[6-7]，取三榀索托桁架为研究对象，结构整体示意如图1所示。该索托桁架为体外施力式索托桁架结构[8]，索体从主体钢结构的底部穿过，拉索两端锚固在边柱上，斜向索与水平向的夹角(所谓索夹角)θ为20°。为了保证边柱不会因为索的张拉而发生侧向位移，柱主要以轴力为主，在每根边柱从柱顶往外侧拉一根索，拉索与竖直方向的夹角为17°，从地面锚固到边柱为11 m，见图1。

桁架平面布置和立面布置如图 2所示，上弦杆

外侧一列从左到右分别为S1到S31，内侧一列从左到右分别为S32到S62，下弦杆从左到右分别为X1到X30，桁架上部竖杆从左到右分别为P1到P32，桁架上部斜杆从左到右分别为Q1到Q32。腹杆编号从左到右分别为F1到F124。桁架各杆件及索的具体材料属性如表1 所示。

图1　索托桁架结构计算模型示意图(单位：m)Fig.1　Calculation model of cable supported truss structure(unit:m)

表1　结构构件材料属性

1.2荷载条件

1.2.1桁架荷载

结构自重由软件分析程序自动考虑，恒载Gk取1.5 kN/m2(不含自重)，按 《建筑结构荷载规范》 取不上人屋面活荷载Qk取0.5 kN/m2，计算杆件内力和结构挠度分别采用以下荷载工况：

工况1：1.35Gk+0.98Qk=2.515 kN/m2

工况2：1.0Gk+1.0Qk=2.0 kN/m2

计算杆件内力时，荷载值取2.515 kN/m2，索托桁架间距为6 m，桁架节间间距为3 m，换算成节点荷载等于22.635 kN。由于计算模型是三榀桁架，桁架之间用钢管链接，桁架结构水平刚度得到提高，这与真实地模拟实际工程中结构的水平刚度足够大相符，不会发生侧向失稳，故只考虑竖向力作用。

1.2.2拉索张力

为使索与主体钢结构协调工作，需要对索施加适当的张力。结构在施工和工作阶段是两种不同的状态：1)施工状态，即初始平衡状态，此时结构受自重、部分施工荷载和预应力的作用；2)工作状态，结构在自重、外部荷载和预应力作用下的平衡状态。考虑到结构在工作状态下的挠度和应力比初始状态下大，对拉索施加张力时只考虑结构在工作状态下的受力情况，即结构在自重、外部荷载和预应力作用下的受力状态，结构内力和挠度分别用荷载工况1和工况2计算。

为了找到合理的张拉值，本文通过有限元分析，在纯桁架、拉索零张力与某数值张力3种情况下对结构的挠度、杆件与索的应力比进行控制对比。计算结果如表2所示，经过对比可得，桁架结构在拉索350 kN张拉下，主体结构的挠度以及内力得到很好的改善，索与主体钢结构能良好地协调工作。说明桁架各杆件截面，拉索截面以及施加的张力取值得当，所以本文通过初始应变法来对索施加350 kN的张拉力。

表2　不同情况下结构的变形以及杆件应力

2　四种索托节点数值模拟方法

本文用ANSYS建立三榀桁架，如图3所示。为了更真实地模拟实际工程中索托桁架结构的受力状态，索托结构中索的力学分析模型要满足大位移、小应变假定，计算时考虑大变形和应力刚化的影响[9-11]在ANSYS索托桁架模型中，根据构件受力不同，采用不同的单元模拟。桁架上弦杆和下弦杆在荷载作用下，除了产生轴力以外，还会产生弯矩和剪力，故采用Beam188单元；边柱同样采用Beam188单元；桁架腹杆主要受轴力，弯矩和剪力很小，故采用Link8单元；拉索由于只能承受拉力，故采用Link 10单元。

图3　有限元模型立体图Fig.3　The space diagram of finite element model

2.1自由度耦合法[5]

自由度耦合法是将连续索与其他构件的连接处分开设置节点，并将此两节点沿两侧拉索夹角平分线方向上的自由度耦合在一起，通过ANSYS有限元方法求解。这种方法能解决连续索滑移问题，操作简单但模拟不了索托节点处拉索与主体钢结构的摩擦接触。

2.2自由度耦合加弹簧的方法[6]

利用自由度耦合和变刚度弹簧单元来处理滑移索摩擦问题，即将拉索与桁架结构接触的节点与桁架上对应节点在切线方向建立变刚度弹簧单元，径向进行自由度耦合。在索滑动时，弹簧的内力即为滑道两端索力之差(即该处的摩擦力)在弹簧方向上的分量。若无摩擦滑动，则弹簧刚度为零。若有摩擦滑移，则切线方向相当于布置了一有刚度的弹簧，弹簧刚度由试验得到的摩擦力与滑移距离关系确定，索托节点模型如图4所示。

图4　索托节点构造有限元模型示意图Fig.4　The finite element model of cable supported joint

文献[12]对预应力索-钢转换节点进行力学性能分析、足尺模型试验研究和ANSYS模拟分析，总结了预应力损失、摩擦系数的变化规律。预应力损失的试验测试结果可供此类预应力钢结构工程参考。

应用试验结果，采用具有非线性功能的单向弹簧单元Combin39来模拟变刚度单元，并对其输入力-变形曲线，实现利用自由度耦合和变刚度弹簧单元来处理滑移索摩擦问题。

2.3点-点接触法[3]

点-点接触方法是将拉索与桁架接触的节点、桁架上对应的节点分开建立，在两段拉索夹角平分线的方向上两个节点间有一个较小的距离，然后用Contact52单元将两点连接起来。Contact52单元的一些主要输入参数有：法向刚度KN、粘性刚度KS、初始条件START、摩擦系数MU。

2.4不变刚度短梁法

本文提出一种新的索托节点数值模拟方法，即不变刚度短梁法。该方法的基本原理是：短梁与主梁钢结构的链接是刚接，短梁本身有一定的抗弯刚度但很小，在对拉索施加预拉力的时候，短梁呈弯曲变形，由于短梁本身具有抗弯能力所以使得两侧索力不相等。短梁的抗弯能力用来模拟索托节点处的摩擦力，采用Beam188/189单元来模拟短梁。

2.4.1短梁法理论

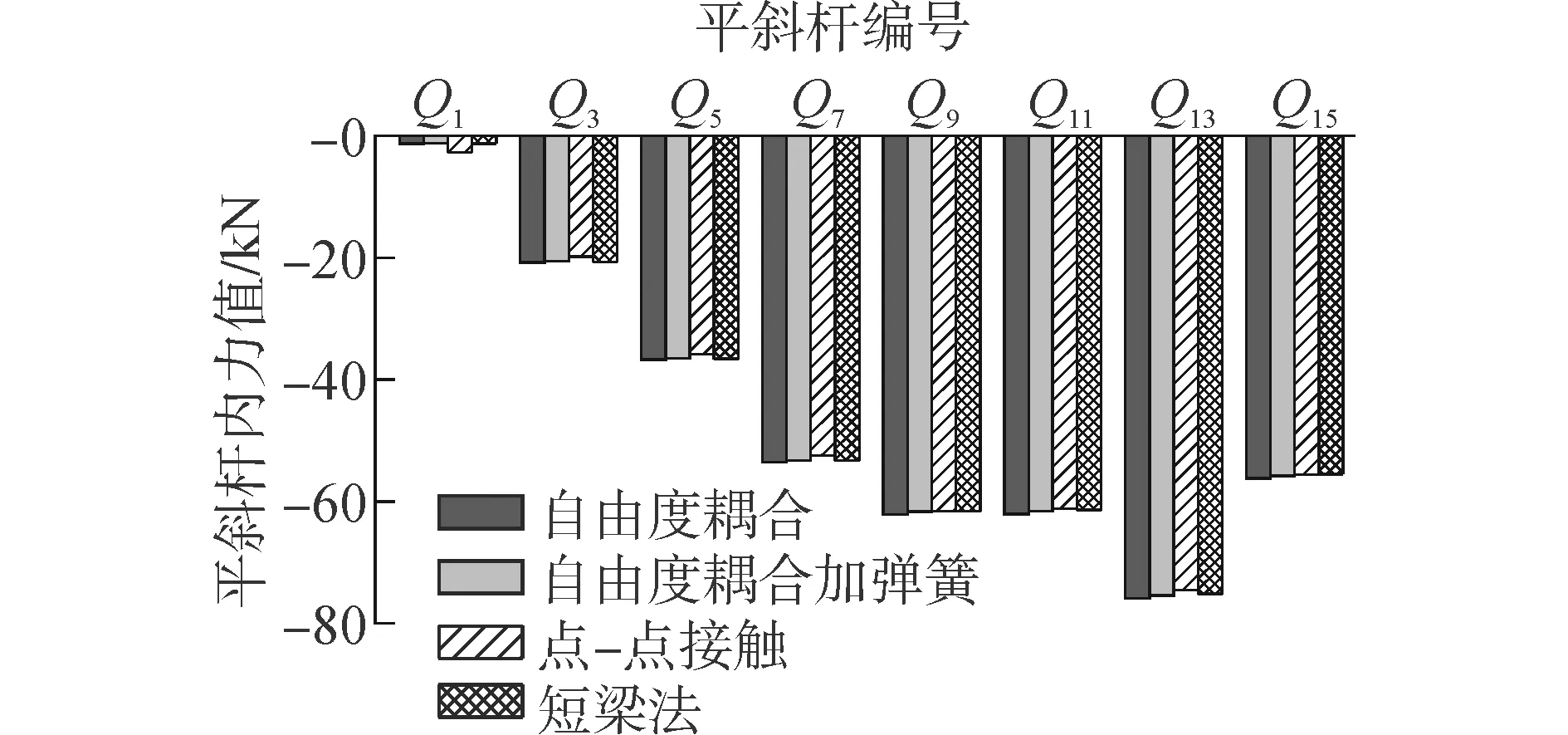
如图5(a)所示，在初始状态时，两侧索的初始张拉均为T0，短梁AO还没变形，结构处于平衡状态。图5(b)中，右侧索施加张力时，由于短梁已有弯曲变形，短梁本身的抗弯能力使两侧索力不相等。右侧索的索力为T2=T0+F，左侧索的索力为T1，T0

(1)

短梁顶端O的水平位移为左边索在(T1-T0)作用下的伸长量：

(2)

采用结构力学的位移法，求得短梁顶端O点所受到的剪力为

(3)

式(3)体现了短梁的抗弯刚度与拉索几何参数及抗拉刚度的关系。假如短梁截面是矩形，而且b=h(宽=高)，那么短梁截面尺寸为

(4)

从式(4)可知，该方法的实质是根据摩擦损失值FS和拉索在索托节点处的滑移量Δ来确定短梁的刚度(短梁的长度和截面尺寸)。该方法不用建立复杂接触，较为简便灵活，故本文提出此方法并进行研究，验证其可行性。

图5　拉索受力简图Fig.5　Diagram of cable force analysis

2.4.2短梁法应用

把上述短梁理论应用在本文索托桁架结构中的索托节点，如图6所示，索夹角为θ，给拉索的初始张拉力为T0，在结构自重以及外荷载作用下，结构有竖向位移，拉索长度变长，使拉索的预应力变大，由于索托节点处摩擦力的存在，导致两侧索力不相等，即T2>T1>T0。因为结构具有两个索托节点，所以索托节点处拉索的滑移量就是水平索在(T1-T0)作用下的伸长量的一半，即

(5)

图6　有限元模型中拉索的受力状态Fig.6　Cable load condition in a static finite element model

如图7所示，短梁是在两侧索夹角平分线方向上(所谓径向)建立的。摩擦力使两侧索力不相等，即T2>T1，预应力摩擦损失在切线方向上的分量，即短梁上A点所受到的剪力为

(6)

为了使结构受力更合理，索的效率更高，一般索夹角θ都小于60°，水平索的伸长量近似等于短梁端部A点在其切线方向上的位移，也是索托节点处拉索的滑移量，即

(7)

图7　索托节点处短梁法示意图Fig.7　The short beam method in cable-supported joint

确定了摩擦损失值FS和拉索在索托节点处的滑移量Δ就可以通过式(4)来确定短梁的长度和截面尺寸(假如短梁截面是矩形，b=h)。短梁的长度和截面尺寸要满足一定的条件：

1)短梁的抗弯刚度足够小，为了模拟两侧索力的摩擦损失，一般工程中摩擦损失力约为张拉力的1%～5%；在拉索摩擦损失力和拉索滑移量已知的情况下，可以通过式(8)得到几组短梁的几何参数(l，b，h)。

2)短梁的抗压刚度应足够大，能为主体钢结构提供足够大的支撑力，但短梁本身不被压缩变形；另外，短梁长度不应太长，否则会影响到斜索与水平向的夹角。

本文中的索托桁架结构，拉索的初始张拉力T0=350 kN、θ=20°，在结构自重以及外荷载作用下，拉索预应力在无摩擦情况下达到约775 kN；假如要模拟摩擦力损失为3%，即T2-T1=775×3%=23.25 kN，通过式(6)算出FS≈23 kN。水平索(即中间的拉索)力增加量为T1-T0=775 kN×97%-350 kN≈400 kN，索托节点处拉索的滑移量约为Δ=0.020 m，通过式(8)得到不同短梁长度的不同截面尺，如表3所示，ANSYS分析结果如表4所示。

表3　不同短梁几何参数

表4　不同几何参数短梁的计算分析结果

从表4可知，不同的短梁几何参数组，得到的结构挠度、索力以及拉索的滑移量也不同，但差别不大，短梁的抗压刚度越大，结果差别越小。因为短梁固定在主梁钢结构的的节点上，而非刚度较大的物体上，所以结构在自重以及外荷载作用下，桁架本身也有变形，使桁架上对应的索托节点有了位移变化，导致两侧索力有所偏差。因此，只要短梁的抗压刚度足够大，结构挠度、拉索滑移量以及拉索支撑力都差别不大，只需调整索力摩擦损失值到合理值即可。本文中，先选出一组抗压刚度足够大的短梁几何参数，用ANSYS计算并分析与需要模拟的索力摩擦损失是否接近，用此方法循环直到结果接近，选出较合适的尺寸。

经计算建议短梁在压力(拉索给主体结构的支撑力)作用下，轴向压缩量不宜大于1 mm。本文中，拉索提供的支撑力约(T1+T2)sinθ/2≈265kN，短梁的抗压刚度应大于265 MPa，经过计算和挑选，最终选择短梁截面尺寸为b=h=0.010 4m，长度l=0.080 m。

3　4种模拟方法的结论对比

本文通过ANSYS建立了4种索托节点模拟方法(自由度耦合加变刚度弹簧方法已得到验证)，得到索托桁架结构的杆件内力，结构竖向位移，索力摩擦损失以及拉索的滑移量，并对计算结果进行了分析和对比，最后对每种方法进行评估，旨在找出较简单且能满足工程精度要求的索托节点建模方法。

由于索托桁架结构左右对称，作用荷载也是对称的，左右对称杆件受力基本相同，故本文只列出左半部桁架杆件的内力及左边斜向索和水平索的索力。

3.1结构整体变形及索力的对比

经ANSYS计算可得利用4种不同索托节点模拟方法计算得到的桁架结构整体最大竖向位移，同时计算出索托节点处拉索的滑移量及索力，如表5所示。

表5　桁架结构整体和索托节点的分析结果

根据表5的数据可得如下结论：

1) 不同索托节点建模方法计算得到的结构整体竖向位移和变形差别不大，4种方法均能为桁架提供的支撑力。

2) 自由度耦合方法不能模拟索托节点处的非线性摩擦，所以两侧索相等，由于拉索可以无摩擦滑移，索托节点处的滑移量最大。

3) 自由度耦合加弹簧法、点-点接触法及短梁法都可以模拟索托节点处的索力摩擦损失，计算两侧索力，索力摩擦损失以及滑移量差别不大，均可进行参数控制，更接近工程中索托节点的摩擦情况。

3.2索托桁架结构构件内力的对比

经ANSYS计算可得4种不同索托节点模拟方法下索托桁架结构构件内力，杆件类别分别为：上弦杆、下弦杆、腹杆、平直杆、平斜杆，对各种杆件的内力值进行分析和对比。

3.2.1上弦杆内力

根据图8对比分析可知：4种方法计算得到的上弦杆内力变化趋势基本一致，结果基本吻合，并且4种方法所得上弦杆内力差别不明显，不同方法影响较小。

3.2.2腹杆内力

由于腹杆受压杆和受拉杆相间存在，本文中腹杆内力分两组列出：A组编号是1、2、5、6、…、57、58、61、62；B组编号是：3、4、7、8、…、55、56、59、60 。计算结果如图9所示。

由图9可得：腹杆的内力走势与文献[9]里的结论相符，桁架腹杆受拉与受压杆件相间分布，腹杆在索托节点处内力降低。4种方法计算出来的腹杆内力值非常相近，说明4种方法对腹杆内力影响较小。

图8　4种索托节点模拟方法计算的上弦杆的内力值Fig.8　Internal forces of upper chord under calculated by four methods

图9　4种索托节点模拟方法计算的腹杆内力值Fig.9　Internal forces of web member calculated by four methods

3.2.3下弦杆

由图10可得：与上弦杆和腹杆内力相比，4种方法对下弦杆影响相对明显，但内力结果基本吻合，变化趋势也一样。因此4种方法对下弦杆内力影响较小。

图10　四种索托节点模拟方法计算的下弦杆内力值Fig.10　Internal forces of lower chord calculated by four methods

3.2.4桁架上部的平直杆和平斜杆内力

由图11和12可得桁架上部的平直杆都是受拉杆，平斜杆都是受压杆，这两种杆件受力较小。这两种杆件从桁架端部到桁架跨中，杆件内力慢慢变大，4种方法计算出来的内力变化趋势一样，结果基本吻合。

3.3评价4种索托节点模拟方法

1) 自由度耦合方法在一定程度上简化了索托节点问题，并被一些实际工程设计所采用，但是由于没有考虑索单元与主体结构之间的非线性摩擦力，计算分析方法略显粗糙，与实际情况有一定差别。

2) 自由度耦合和变刚度弹簧单元来处理滑移索摩擦问题的方法，弹簧采用Combin39单元，可以模拟不同的摩擦系数。该方法理论明确，计算易收敛，并在2008年奥运会羽毛球馆的实际工程算例中得到验证，是目前为止较为合理的方法[13]。

图11　四种索托节点模拟方法计算的平直杆内力值Fig.11　Internal forces of straight rod calculated by four methods

图12　四种索托节点模拟方法计算的平斜杆内力值Fig.12　Internal forces of inclined rod calculated by four methods

3) 点-点接触法属于非线性接触分析，一般的通用有限元软件可以提供接触单元，利用接触单元处理接触滑移，但这种方法考虑非线性接触行为，计算工作量大，计算方法较复杂，适用于滑移索的单个节点分析，不适用于带滑移索的整体结构体系分析，不便于一般工程技术人员掌握。

4) 短梁方法：通过本文4种方法的对比和分析可知短梁方法是可行的，可以通过改变短梁的长度和截面面积来调整索托节点处拉索的摩擦损失力。短梁刚度不变，计算更简单，计算效率较高，并且该方法的理论明确，工程人员更容易理解和掌握。但这种方法需要在拉索的张拉力和摩擦情况已知的情况下才能确定短梁的几何参数。

4　结论

1) 本文通过对4种索托节点数值模拟方法(自由度耦合方法、自由度耦合加变刚度弹簧单元方法、点-点接触方法和不变刚度短梁法)的分析计算可知：由于索托节点处的摩擦力小(约为张拉力的1% ～ 5%)，所以4种方法对桁架结构挠度和构件内力引起的差别不是很明显，结果基本吻合，内力走势一样。其中，自由度耦合加变刚度弹簧单元方法在2008年奥运会羽毛球馆的实际工程算例中得到验证，进而说明本文新提出的不变刚度短梁法是合理可行的。

2) 通过对4种索托节点模拟方法的评价可知：自由度耦合加弹簧方法可以模拟不同的摩擦系数；短梁方法可以通过改变短梁的长度和截面面积来调整索托节点处拉索的摩擦损失力。这两种方法能更好地模拟索托节点处的摩擦力，理论明确且计算简单方便，是相对较好的索托节点数值模拟方法。

[1]胡沛铭. 索托桁架结构延性设计研究[D]. 北京: 北京交通大学, 2014.

HU Peiming. Research on the ductility design of cable-supported truss structure[D]. Beijing: Beijing Jiaotong University, 2014.

[2]MALERBA P G, GALLI P, DI DOMIZIO M, et al. A large span roof made of cable stayed arches[C]//Proceedings of ARCH′10-the 6th International Conference on Arch Bridges. Fuzhou, China, 2010.

[3]陈丹. 索托结构关键问题研究[D]. 北京: 北京交通大学, 2010.

CHEN Dan. Study on key problems of cable-supported structure[D]. Beijing: Beijing Jiaotong University, 2010.

[4]张阿鹏. 索托结构静力和抗震性能的研究[D]. 西安: 西安建筑科技大学, 2007.

ZHANG Apeng. Study on static and aseismic behaviors of cable-held structure[D]. Xi’an: Xi’an University of Architecture and Technology, 2007.

[5]杨维国, 邹清, 李兴坡, 等. 索托结构中拉索预应力水平的优化研究[J]. 中国矿业大学学报, 2012, 41(2): 219-224.

YANG Weiguo, ZOU Qing, LI Xingpo, et al. An optimized pre-stress level for the design of cable supported trusses[J]. Journal of China university of mining & technology, 2012, 41(2): 219-224.

[6]席根喜, 徐国彬. 索托结构在芦城体校曲棍球馆的应用[J]. 空间结构, 2010, 16(3): 60-63.

XI Genxi, XU Guobin. Application of cable-held structure in hockey stadium of Beijing Lucheng Physical Training School[J]. Spatial structures, 2010, 16(3): 60-63.

[7]侯俊. 北京芦城体校曲棍球训练馆索托结构施工技术[J]. 工程施工技术, 2007(6): 89-93.

HOU Jun. Construction technologies of cable-supported structure in Beijing Lucheng physical training school hockey training hall[J]. Construction technology, 2007(6): 89-93.

[8]谷鹏. 索托桁架结构性能影响因素分析[D]. 北京: 北京交通大学, 2011.

GU Peng. Study on the influencing factors of cable-supported truss structural performance[D]. Beijing: Beijing Jiaotong University, 2011.

[9]王新敏. ANSYS工程结构数值分析[M]. 北京: 人民交通出版社, 2007: 6-14.

[10]SONG M K, KIM S H, CHOI C K. Enhanced finite element modeling for geometric non-linear analysis of cable-supported structures[J]. Structural engineering and mechanics, 2006, 22(5): 575-597.

[11]LI Fengchen, ZHANG Lina, TIAN Shizhu, et al. Analysis of identified cable force of cable-stayed bridge[C]//Proceedings of the 2nd International Conference on Transportation Engineering. Chengdu, China, 2009: 3020-3025.

[12]张国军, 葛家琪, 谷鹏, 等. 预应力大悬挑钢结构索-钢转换节点足尺模型试验与设计研究[J]. 建筑结构, 2010, 40(12): 34-40, 83.

ZHANG Guojun, GE Jiaqi, GU Peng, et al. Full-scale model experiment and research of large span prestressed cable-member transfer connection[J]. Building structure, 2010, 40(12): 34-40, 83.

[13]王树, 张国军, 葛家琪, 等. 2008奥运会羽毛球馆预应力损失对结构体系影响分析[J]. 建筑结构学报, 2007, 28(6): 45-51.

WANG Shu, ZHANG Guojun, GE Jiaqi, et al. Influence of prestress loss on structural behavior of the badminton gymnasium for 2008 Olympic Games[J]. Journal of building structures, 2007, 28(6): 45-51.

本文引用格式：

杨维国, 王萌, 王亚,等. 索托节点的数值模拟方法研究[J]. 哈尔滨工程大学学报, 2016, 37(8): 1050-1056.

YANG Weiguo, WANG Meng, WANG Ya, et al. Study of numerical simulation methods for cable-supported joints[J]. Journal of Harbin Engineering University, 2016, 37(8): 1050-1056.

Study of numerical simulation methods for cable-supported joints

YANG Weiguo, WANG Meng, WANG Ya, RUAN Zhiyong

(School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China)

To more accurately simulate cable-supported joints, in this study, we simulated an overall truss by using ANSYS model, and carried out finite element method (FEM) analyses. As a new method, the constant stiffness short beam method was advanced for simulating cable supported joints. It was also compared with other three methods, the degree-of-freedom coupling method, the degree-of-freedom coupling with variable stiffness spring method, and the joint-joint contact method. The results show that: there are no obvious differences in the deformation and internal forces for the four methods, which are basically same. The trend of the internal forces is consistent. Because the free coupling with variable stiffness spring method has been verified, the proposed constant stiffness short beam method we proved is both reasonable and feasible. The degree-of-freedom coupling with variable stiffness spring method and the constant stiffness short beam method can better simulate the friction forces in cable-supported joints, which represents a better way to model cable-supported nodes, and the theory underlying these two methods is clear and convenient.

cable-supported joints; numerical simulation; constant stiffness short beam method; degree-of-freedom coupling method; variable stiffness spring; joint-joint contact method; friction force

2015-05-09.网络出版日期：2016-06-23.

国家自然科学基金项目(51178041)；中央高校基本科研业务费专项资金项目(2011JBM260)；中国航空规划建设发展有限公司项目(技13研-51).

杨维国(1973-), 男, 教授, 博士;

王亚(1990-), 女, 博士研究生.

王亚，E-mail:wangya_73@163.com.

10.11990/jheu.201505025

TU393.3

A

1006-7043(2016)08-1050-07