舰船典型结构冲击仿真模型前处理方法研究
王乾勋, 冯麟涵, 杜志鹏, 张 磊
(1.沈阳工业大学 机械工程学院, 辽宁 沈阳 110870; 2.海军装备研究院, 北京 100161)
舰船典型结构冲击仿真模型前处理方法研究
王乾勋1, 冯麟涵2, 杜志鹏2, 张磊2
(1.沈阳工业大学 机械工程学院, 辽宁 沈阳 110870; 2.海军装备研究院, 北京 100161)
有限元仿真方法是研究和考核舰船结构及舰载设备抗冲击的重要手段,板梁是舰船及其设备中最普遍的结构,其仿真精度对舰船抗冲击设计有重要影响。设计了不同尺寸的悬臂梁和板架结构,在相同的冲击环境下进行了冲击试验和不同前处理方法的仿真计算,通过对比试验与仿真结果,研究了有限元单元的长宽比、形状、类型、求解方法、单元耦合方式等前处理方法对于板梁结构冲击仿真精度的影响。研究得到:单元长宽比接近1∶1、采用缩减积分、实体与壳体耦合等方法能有效提高仿真精度,对舰船结构的有限元仿真提供一定参考。
抗冲击板梁结构冲击试验前处理方法
0 引言
美国、德国、荷兰、英国和法国等国家一般采用冲击试验和数值模拟相结合的方法对舰船设备抗冲击能力进行考核[1-5]。我国对舰船设备抗冲击性能的研究与考核发展较晚,考核所采用的技术手段主要借鉴欧美等国家的考核方法。由于经济条件和试验条件等限制,加上仿真计算考核方法具有周期短、成本低、易实施和不受环境条件限制等优点。国内多以仿真计算为主,考核为辅。
模型前处理的质量对仿真计算结果的可靠性有重要影响,高质量的前处理结果能够显著缩短求解时间进而缩短仿真考核的周期,进一步为模型优化创造良好的前期基础,减轻设计人员的工作量[6-8]。因此,模型前处理方法就显得尤为重要。
舰船中存在着大量的悬臂梁和板架结构,将这两种结构作为研究对象具有一定代表性[9-12]。为了探讨不同前处理方式对舰船设备的冲击破坏机理,设计了不同尺寸的悬臂梁和板架结构。结合试验结果,分析不同前处理方法中悬臂梁和板架在相同冲击载荷下的应力响应,进而研究前处理方法对板梁结构冲击仿真精度的影响。
1 梁模型和板架模型
1.1模型简介
悬臂梁模型如图1(a)所示,长度为L,宽度为B,厚度为H,其材料为Q235钢,弹性模量E=206 GPa,泊松比μ=0.3,密度ρ=7 850 kg/m3。板架模型如图1(b)所示,由底板、中间板、上板、下竖板1、下竖板2、上竖板1、上竖板2(2块)和子配重块(8块)组成,其材料与悬臂梁相同。

图1 悬臂梁模型与板架模型
为了更细致地研究梁的长、短、薄、厚在进行前处理后冲击计算的应力响应规律,设计了11套不同尺寸的梁模型,并取其一阶固有频率,参数如表1所示。图2为梁模型的实物图。

表1 梁的参数

图2 梁实物图
板架结构模型共计5套,5套板架模型只有在上竖板1和上竖板2位置处的厚度不一样,具体数值如表2所示,图3为板架实物图。

表2 板架的参数

图3 板架实物图
1.2抗冲击试验测点布置
将梁模型结构和板架模型结构安装于冲击机台面上,进行冲击试验。试件通过8.8级六角螺钉配合双耳止动垫片装配于冲击机台面。测点布置方案如图4所示,悬臂梁模型共有2个加速度测点和4个应力测点;板架模型结构共有3个加速度测点和3个应力测点。

图4 梁与板架模型测点布置图
梁模型与板架模型试验安装图如图5所示,整个系统由冲击机控制柜、液压泵站、测试电脑、加速度传感器、应变片、电源、冲击台、信号采集仪以及支撑架构成。

图5 梁与板架模型试验安装图
2 冲击试验及结果
2.1冲击环境
根据德国军标BV043-85中对设备冲击考核冲击环境的相关规定,将三折线谱转换为如图6所示正负双波时域冲击加速度信号,该信号由正负两个面积相等的半正弦波组合而成,图中横坐标为时间,纵坐标为加速度,将该载荷施加于设备的固定端。

图6 正负双波时域冲击加速度信号
式 (1)~式(5)为设计谱值与时域信号的转化关系式:
(1)
(2)
(3)
(4)
(5)
式(1)~式(5)中:A为极限谱加速度;V为极限谱速度;D为极限谱位移[13]。
结合大量相关冲击试验的结果,以及现有最新研制的500 kg正负双波冲击机的承载能力,定制冲击环境主要参数如下:谱加速度A0=150 g;谱速度V0=4.5 m/s;谱位移D0=4 cm;重力加速度g=9.8 m/s2。
将A0、V0和D0这三个参数代入式(1)~式(5)中,计算得出双重正弦变化时间历程曲线中各个参数值如下:
a2=735 m/s2;a4=232.65 m/s2;t1=6.41 ms;t2=20.26 ms;V1=V2=3 m/s。
2.2试验结果
对11套梁模型和5套板架模型,通过冲击试验机施加2.1节中设计的正负双波时域冲击加速度信号,分别得到悬臂梁模型和板架模型测点的应力值,如表3、表4所示,表中“-”表示由于模型尺寸引起的无效测点。

表3 梁的试验结果

表4 板架的试验结果
3 梁模型前处理方法研究
选取8号梁作为研究对象,8号梁的试验结果最大应力响应为83.98 MPa。模型进行网格划分时涉及到单元的长宽比、网格的形状(三角形或四边形等)、网格的类型(二维网格/三维网格)、单元的求解技术等诸多方面,逐一研究这些因素对设备冲击计算精度的影响。
3.1单元长宽比对冲击计算精度的影响
在有限元软件ANSYS中采用平面单元PLANE 182对梁模型进行网格划分,不同长宽比网格划分后的有限元模型如图7所示,长宽比依次为1∶1、5∶1、10∶1、15∶1和20∶1。

图7 梁设备有限元模型对比图
仿真冲击载荷与试验载荷保持一致,计算后提取梁固定端的最大应力响应,绘制出应力响应与单元长宽比的关系曲线,如图8所示。

图8 应力响应与单元长宽比的关系
图8中可以看出,梁固定端的应力响应随着单元长宽比的增加而降低。在长宽比1∶1~5∶1之间,最大应力响应下降的速度较快;在长宽比5∶1~20∶1之间,最大应力响应下降速度相对缓慢;将试验结果与仿真计算结果进行对比,得到长宽比为1∶1时的仿真结果与试验数据最接近,误差为11.49%。
3.2网格的形状对冲击计算精度的影响
同样在有限元软件ANSYS中采用平面单元PLANE 182对梁模型进行网格划分,网格的长宽比设置为1∶1,网格分别为三角形自由网格、三角形映射网格和四边形网格,如图9所示。
护理前两组患者的空腹血糖、餐后2 h血糖和糖化血红蛋白水平的检测结果差异无统计学意义(P>0.05);但在护理后观察组患者的空腹血糖、餐后2 h血糖和糖化血红蛋白水平的检测结果都明显低于对照组(P<0.05)比较差异有统计学意义。见表1。
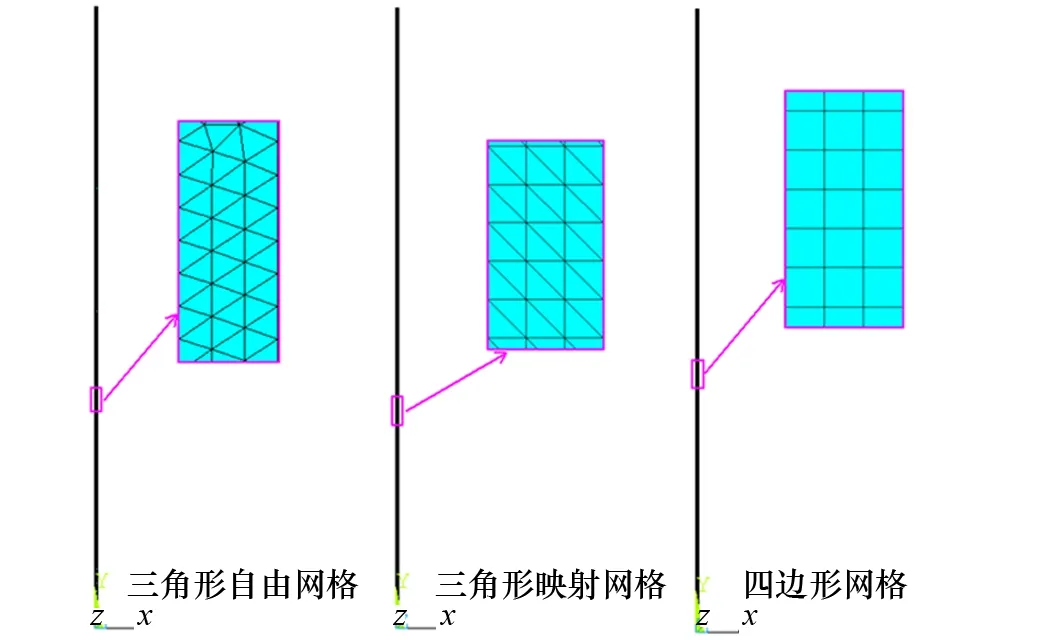
图9 不同网格形状的有限元模型
计算后提取梁固定端的最大应力响应,绘制出应力响应与网格形状的关系图,如图10所示。
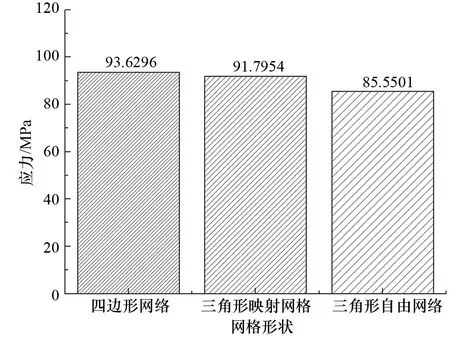
图10 网格形状与应力的关系
从图10中可以看出,仿真得到的应力按从大到小顺序依次为四边形网格,三角形映射网格,三角形自由网格。通过与试验结果的对比,四边形网格的误差最大为11.49%,三角形映射网格误差为9.31%,三角形自由网格误差最小为1.87%。
3.3网格类型对冲击计算精度的影响
对梁模型分别用二维四边形单元、三维四面体、三维六面体进行网格划分,然后对其进行冲击仿真计算。得到应力响应与网格类型的关系,如图11所示。

图11 网格类型与应力的关系
从图11中可以看出,仿真得到的应力按从大到小顺序依次为四面体网格,四边形网格,六面体网格。与试验结果进行对比,四边形网格的误差为11.49%,四面体网格的误差为15.80%,六面体网格的误差为7.21%。
3.4单元求解技术对冲击计算精度的影响
对梁模型采用三维四面体网格进行前处理,利用有限元软件ANSYS进行冲击仿真计算,选择单元的类型为SOLID 185号单元,依次采用:完全积分法(Full integration)、缩减积分法(Reduce Integration)、增强应变公式法(Enhanced Strain)和简单的增强应变公式法(Simple Enhanced Strain)进行计算。计算后的应力响应结果如图12所示。

图12 单元求解技术与应力的关系
3.5单元大小对冲击计算精度的影响
有限元软件ANSYS中采用平面单元PLANE 182对梁模型进行网格划分,网格的长宽比设置为1∶1,网格大小依次设置为1 mm、2 mm、3 mm、4 mm、5 mm、6 mm和10 mm。将冲击载荷施加于梁模型的固定端,计算后提取梁固定端的最大应力响应,绘制出应力响应与单元大小的关系图,如图13所示。

图13 单元大小与应力的关系
从图13中可以看出,梁固定端的应力响应随着单元大小的增加而降低,在单元大小1 mm~3 mm之间应力下降最快,3 mm~10 mm之间下降相对较慢, 将仿真数据与试验结果进行对比, 网格大小为10 mm时的误差最大为20.44%,网格大小为2 mm时的误差最小为3.32%。
4 板架结构模型前处理方法研究
对板架结构模型主要研究网格单元类型对冲击计算结果的影响,对所设计的板架进行全实体和实体与壳体结合两种网格划分方式,同时保证网格尺寸均相同,实体网格采用Solid 185单元,壳体采用Shell 181单元,进而研究网格单元类型对设备冲击破坏的影响。板架有限元模型如图14所示。
将冲击载荷施加于板架结构底板的下表面,计算后提取板架结构应力测点3的最大应力响应结果,如表5所示。
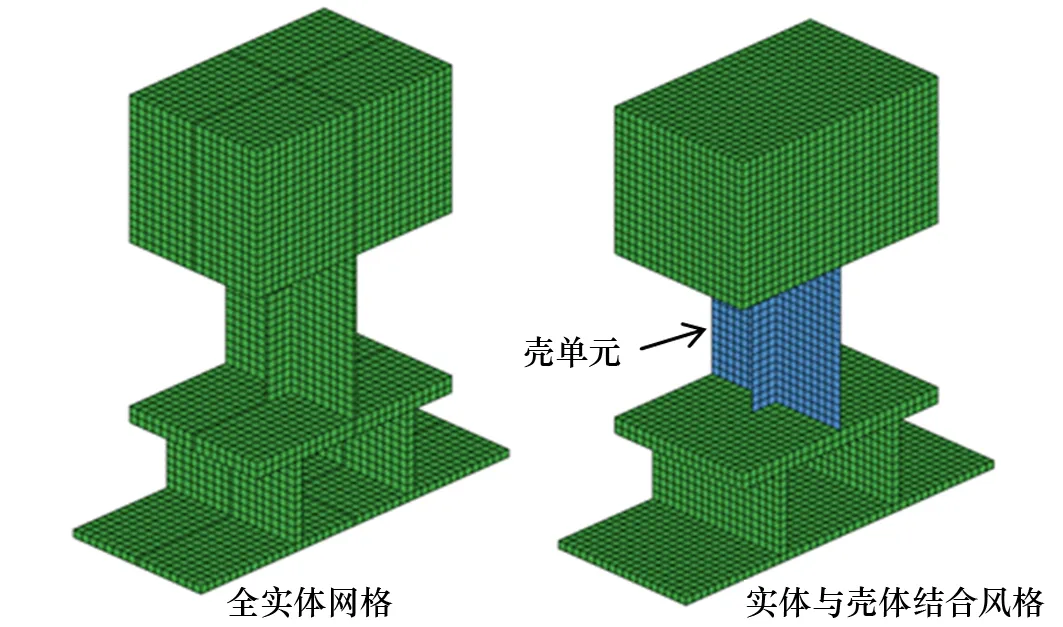
图14 板架结构有限元模型
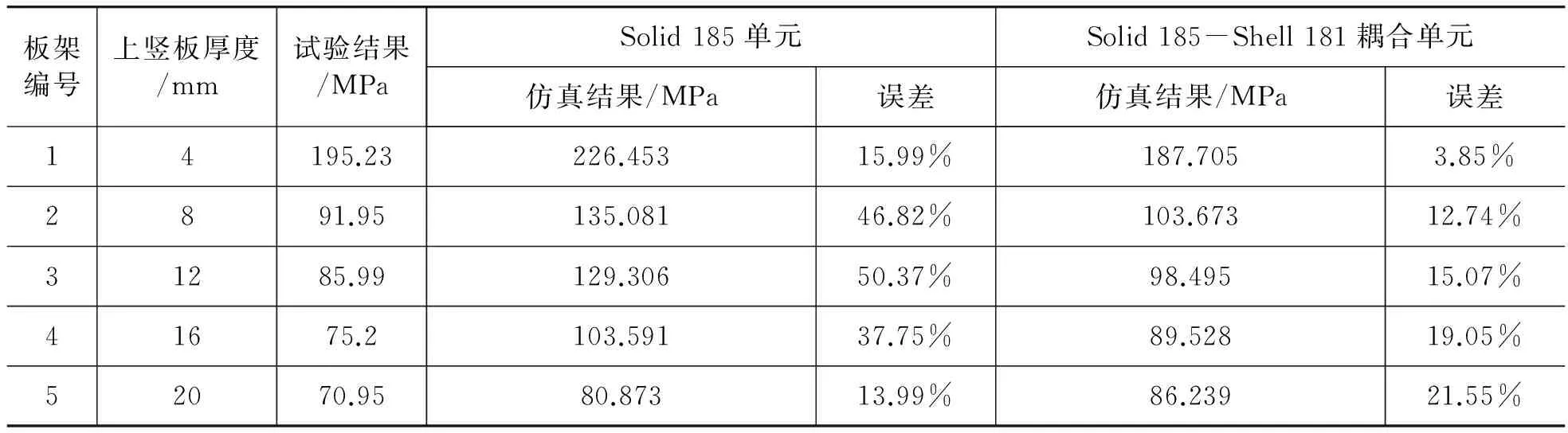
板架编号上竖板厚度/mm试验结果/MPaSolid185单元Solid185-Shell181耦合单元仿真结果/MPa误差仿真结果/MPa误差14195.23226.45315.99%187.7053.85%2891.95135.08146.82%103.67312.74%31285.99129.30650.37%98.49515.07%41675.2103.59137.75%89.52819.05%52070.9580.87313.99%86.23921.55%
与上竖板连接的板为中间板,其厚度为20 mm,当上竖板厚度小于中间板厚度80%(16 mm)时,实体与壳体结合的网格划分方法计算的结果更加准确有效;当上竖板厚度等于中间板厚度时,实体网格划分方法计算的结果更加精确。
5 结论
(1) 对于悬臂梁,在相同的冲击环境下,长宽比1∶1网格划分的仿真应力结果与试验结果最接近,误差为11.49%,即在舰船板梁结构模拟中,在条件允许的情况下保证网格长宽比接近1∶1,有利于提高仿真精度。
(2) 在梁结构中,对于二维的三角形网格和三维的六面体网格划分,其计算精度明显高于其他划分方法。
(3) 缩减积分法相比于其他计算方法特别适合于板梁的弯曲等变形的仿真计算,相对于试验结果的仿真误差仅为0.7%。
(4) 在板架冲击仿真中,由于板架结构厚度较小,两种板材的厚度比在小于80%时,宜采用壳单元与实体单元耦合或者壳单元与壳单元耦合的方式进行仿真计算。
[1]张健, 万正权, 黄进浩, 等. 舷侧板架与冰体碰撞数值仿真及模型试验研究[J]. 船舶力学, 2014(04): 424-433.
[2]陈长海, 朱锡, 侯海量, 等. 近距空爆载荷作用下双层防爆舱壁结构抗爆性能仿真分析[J]. 海军工程大学学报, 2012(03):26-33,70.
[3]Baskar K, Shanmugam N E, Thevendran V. Finite-element analysis of steel-concrete composite plate girder[J]. Journal of Structural Engineering, 2002, 128(9): 1158-1168.
[4]Shanmugam N E, Lian V T, Thevendran V. Finite element modelling of plate girders with web openings[J]. Thin-Walled Structures, 2002, 40(5): 443-464.
[5]郑少平, 陈静, 程远胜, 等. 代理模型技术及其在船舶板架强度和稳定性计算中的应用[J]. 中国造船,2013(01):40-51.
[6]周红, 张延昌, 岳亚霖, 等. 夹层板系统碰撞性能数值仿真分析技术[J]. 计算机辅助工程,2013(02):66-71,82.
[][]
[7]Nagel G M, Thambiratnam D P. A numerical study on the impact response and energy absorption of tapered thin-walled tubes[J]. International Journal of Mechanical Sciences, 2004, 46(2): 201-216.
[8]陈静, 张攀, 肖汉林, 等. 大型舰艇多学科设计优化船体结构子系统设计方法[J]. 中国舰船研究,2013(05):27-32.
[9]Nagel G M, Thambiratnam D P. Computer simulation and energy absorption of tapered thin-walled rectangular tubes[J]. Thin-Walled Structures, 2005, 43(8):1225-1242.
[10]刘敬喜, 崔濛, 龚榆峰. 船舶碰撞仿真失效准则比较[J]. 中国舰船研究,2015(04):79-85.
[11]谭海涛, 王善, 徐定海. 水下爆炸载荷下舰船舷侧防护结构可靠性分析[J]. 哈尔滨工程大学学报,2009(05):491-494,588.
[12]Faulkner D. The Collapse Strength and Design of Submarines [M]. Int. Symp. Naval Submarines, London, 1983.
[13]汪玉, 华宏星. 舰船现代冲击理论及应用[M].北京: 科学出版社, 2005.
Pretreatment Method Study on Typical Structure Shock Simulation of Ships
WANG Qian-xun1, FENG Lin-han2, DU Zhi-peng2, ZHANG Lei2
(1.Mechanical Engineering School of Shenyang University of Technology, Shenyang Liaoning 110870, China; 2.Navy Equipment Research Institute, Beijing 100161, China)
Finite element simulation is an important means of research and evaluation of ship structure and equipment under shock environment.Plate girder structure is widely used in the ships, so the simulation quality of the plate girder structure makes a significant effect on the shock design of ships. Designed a series of cantilever and board structure, and carried out shock test and simulation under same shock environment, studied the effects on the finite element simulation accuracy of the element aspect ratio, shape, style, solving method, coupling method by comparing the results of test and simulation. It could be found that when element aspect ratio nearly 1∶1, Reduce Integration and solid-shell coupling methods can greatly improve the simulation quality which can be used to guide the finite element simulation of ships.
Shock resistancePlate girder structureShock testPretreatment method
中国博士后科学基金(编号:2014M562622),航空科学基金(编号:201404Q5001)。
王乾勋(1990-),男,硕士研究生,主要从事舰船设备抗冲击设计与研究。
U662
A

