应急决策中基于问题与解关系的案例调整方法
郑 晶, 王应明, 陈圣群
(1. 福州大学 决策科学研究所,福建 福州 350116; 2. 福建江夏学院 电子信息科学学院,福建 福州 350108)
应急决策中基于问题与解关系的案例调整方法
郑晶1,2, 王应明1*, 陈圣群2
(1. 福州大学 决策科学研究所,福建 福州 350116; 2. 福建江夏学院 电子信息科学学院,福建 福州 350108)
针对应急方案调整问题,提出了一种基于案例问题与解决方案之间关系的决策分析方法.通过混合相似度法计算目标案例与历史案例间的综合相似度,并将其融入历史案例的问题与解决方案属性中,进而根据向量余弦夹角定义计算问题与解决方案之间的关系.应急方案调整除需考虑问题与解决方案之间的夹角关系,还需考虑问题与解决方案的模的大小.最后,用算例说明该应急案例调整方法的有效和实用性.
案例推理;应急决策;案例调整;向量余弦夹角
Journal of Zhejiang University(Science Edition), 2016,43(5):560-566
0 引 言
当突发事件发生时,决策者必须快速有效地做出应急响应,最大限度降低突发事件带来的危害,保证生命和财产安全.因此,如何快速做出应急决策是应急管理中最重要的研究内容之一.目前,应急方案生成方法主要有前景理论[1]、故障树分析[2]、博弈论[3]、群决策[4]、案例推理(Case-based reasoning, CBR)[5]、协同决策模型[6]等.由于应急决策中涉及很多专业知识,且需要快速做出响应,决策者普遍认为借鉴历史经验生成应急方案是一种有效的途径.案例推理就是通过寻找与目标案例相似的历史案例,将其解决方案重新应用到当前案例中的方法.因此,案例推理已经广泛应用于应急决策中,例如,LIAO等[7]将其运用于环境应急响应问题中;FAN等[5]将其应用到瓦斯爆炸应急决策中;HUANG等[8]将其应用到应急管理工程中;LIU等[9]将其应用到应急资源管理中等.
已有研究主要针对如何在案例库中检索到与目标案例最相似的历史案例,并将解决方案应用到当前突发事件中.但是,因为历史案例与目标案例存在一定的差异,特别像突发事件如此复杂的问题,历史案例的方案多数情况下不能直接应用于当前突发事件中,因此,案例推理中案例调整的研究引起了学者们的关注.案例调整主要有两类,一类是利用统计方法对问题的解进行调整,例如,QI等[10]根据适应能力度量机制计算解的适应能力得到新问题的解,HU等[11]通过灰色关联方法计算问题与解之间的关系以对新问题的解进行调整,FUCHS等[12]利用微分方法计算问题与解之间的关系获得新问题的解;另一类是利用机器学习方法来提高调整的精确度,例如,LIAO等[7]利用遗传算法来解决问题的适应能力问题,同时克服了案例缺乏的问题,JUNG等[13]应用径向基函数来解决产品设计中问题解的调整问题,SHARIFI等[14]基于支持向量机创建了案例调整模型来解决伺服系统的问题等.在突发事件中,存在历史案例匮乏的情况,且决策过程中需高度依赖专业知识,虽然机器学习可以提高案例调整的精确度,但是需要大量数据及昂贵的计算花费,不适合应用于应急决策中.所以,本文将采用基于统计的案例调整方法,充分利用了其专业知识和使用便利的优点[10].在案例调整中,需要获取问题与解之间的关系,而向量余弦是一种常用的向量比较方法,可以用于任何维度的向量比较中,在高维正空间中的利用尤为频繁.因此,考虑基于问题与解决方案属性的向量余弦关系的案例调整方法,具有重要的意义.
1 问题描述
在考虑基于案例推理的应急决策问题时,为了叙述方便,用N={1,2,…,n}表示历史案例的数量;H={1,2,…,h}表示问题属性的数量;F={1,2,…,f}表示解决方案属性的数量.本文中,案例采用二元组的形式表示,即案例=(问题,解决方案).案例分为目标案例和历史案例,目标案例指当前发生的突发事件,历史案例指存储在案例库中与当前突发事件同类型的用来辅助决策的案例.设C={(X1,Y1),(X2,Y2),…,(Xn,Yn)}表示由n个历史案例构成的案例集,其中(Xj,Yj)表示案例库中的第j个案例,Xj和Yj分别表示历史案例的问题和解决方案,j∈N.记X0表示当前需要解决的突发事件,Y0为当前突发事件待生成的解决方案.
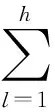
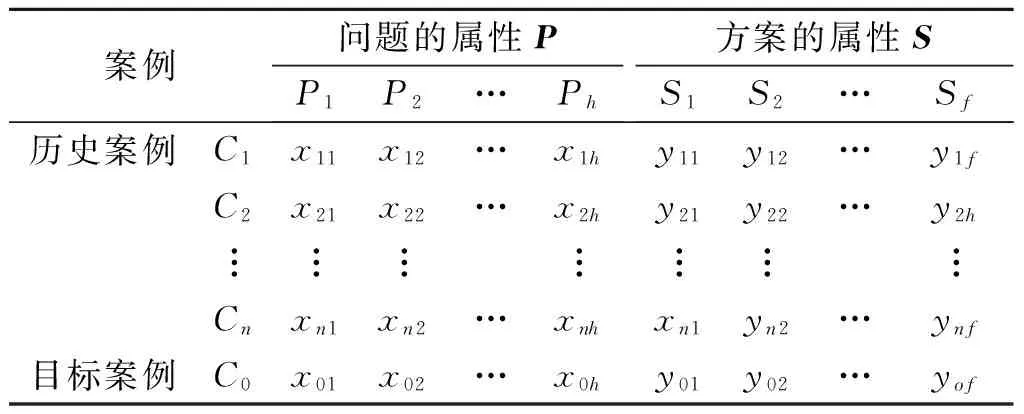
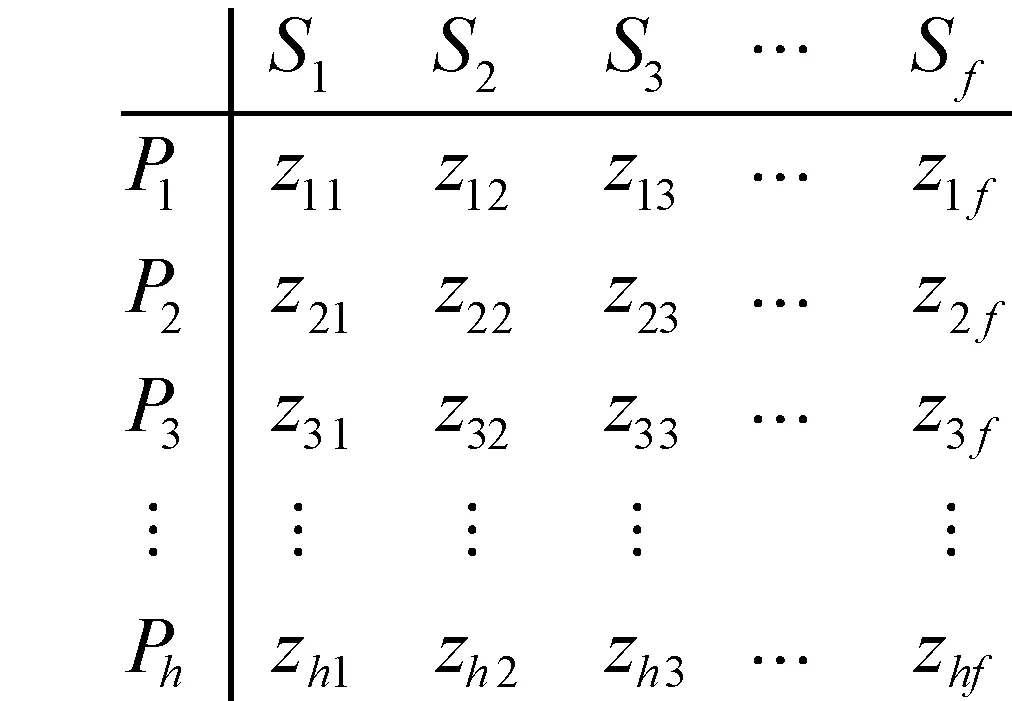
表1 问题和方案的属性值描述
依据现实情况,表1中的属性值xjl通常可分为数值型和语言型2种,yjt一般采用数值型.例如,属性“烧毁面积”一般是数值型;属性“固定消防能力水平”一般是语言型,如采用“极差,差,一般,强,非常强”等语言变量来表示;属性“消防人员”一般是数值型.
本文要解决的问题是:针对当前需要解决的问题X0,依据表1中的历史案例问题与解决方案及问题的属性权重,如何运用一个可行的决策分析方法生成目标案例的应急方案,即得到Y0的值.
2 应急方案生成方法
为了生成有效的应急方案,笔者提出一种基于向量余弦的案例调整方法.如图1所示,首先,通过混合相似度计算方法计算目标案例与历史案例的相似度,并把相似度融入历史案例问题与解决方案属性中;在此基础上,通过余弦定理分析案例的问题与解之间的关系;最后,根据问题与解决方案之间的余弦夹角及其问题与解决方案的模生成目标案例的解决方案.下面分别阐述该方法的计算步骤.
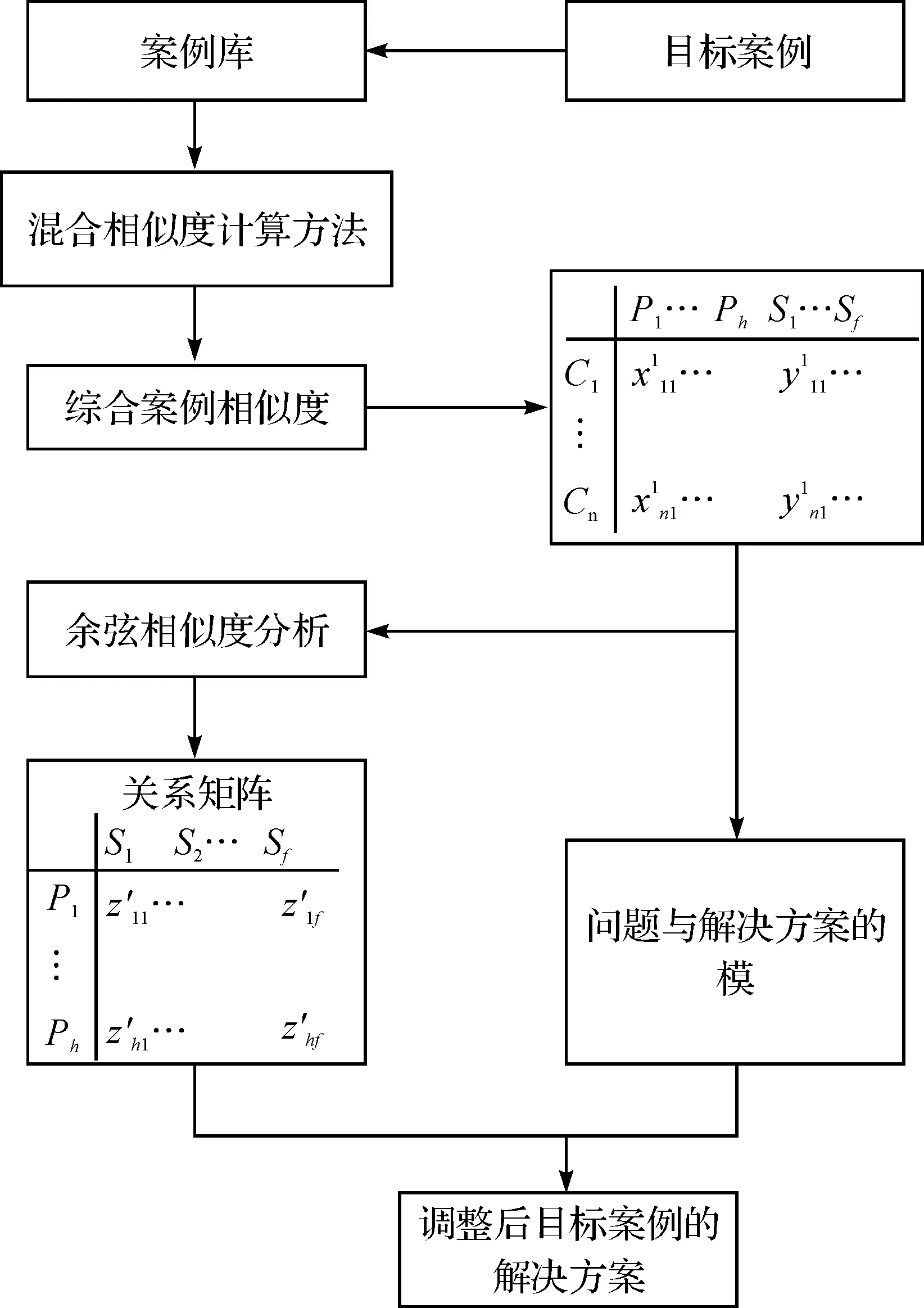
图1 基于问题与解的应急案例调整过程Fig.1 The process of emergency case adaptation based on the relation between the problem and the solution
2.1案例相似度计算
定义1设语言集I={I0,I1,…,Ik,…,In}为一组有序的语言评价值,则其中Ik的三角模糊数为
在案例检索中,相似度计算是一个关键的环节.目前单一检索方法存在一定的限制,但是,通过联合多个检索方法可以打破限制,放大检索的优势[15].目前,基于距离相似度的计算方法有:欧氏距离法[16]、灰关联法[15]、高斯方法[17]、优于关系法[18]等.本文采用将欧氏距离法、灰关联法和高斯方法相结合的相似度计算方法,分别从线性、关联及其非线性的角度获取案例相似度.欧氏距离法是最常用的检索方法,其相似度计算公式为:

(1)

灰色关联法的关联度计算公式为:
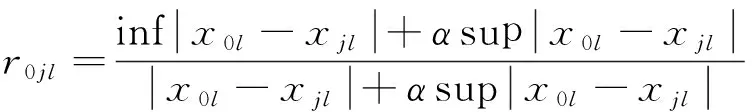
(2)
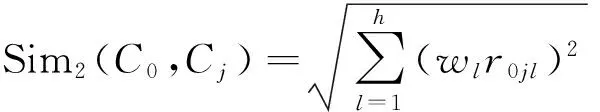
α∈(0,1)为分辨系数,一般的情况下取α=0.5.
高斯法的相似度计算公式为:
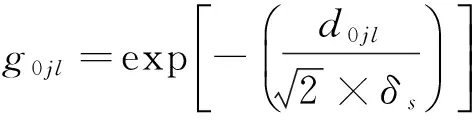
(4)
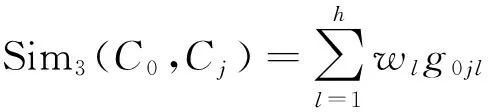
(5)
其中,σs=σ×(max{xjl}-min{xjl}),σ∈[0,1]表示误差偏离程度,max{xjl}和min{xjl}表示第l个属性的最大值和最小值.
上述3种案例相似度计算方法中属性权重wl的确定方法有熵权法[20]、Delphi法[21]、机器学习优化方法[22]、数学模型优化方法[20]等.其中ZHAO等[20]提出的基于属性距离的权重优化方法不仅可以客观地确定权重,而且易于求解.因此,本文采用该方法.基于属性距离的权重优化模型如下:
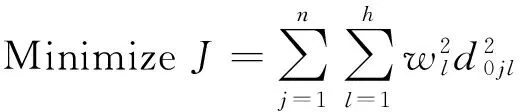
(6.1)

(6.2)
0≤wl≤1,
(6.3)其中,式(6.1)为目标函数,含义是最小化所有案例的带权属性距离,式(6.2)表示权重之和为1,式(6.3)表示属性权重的取值范围.
进一步,对上述3种案例的相似度进行集结得到综合案例相似度Sim(C0,Cj),其计算公式为
Sim(C0,Cj)=γSim1(C0,Cj)+βSim2(C0,Cj)+
θSim3(C0,Cj),
(7)
其中,γ+β+θ=1,0≤γ,β,θ≤1.显然,Sim(C0,Cj)∈[0,1],Sim(C0,Cj)越大,表明历史案例Cj与目标案例C0的相似度越高.
最后,对综合案例相似度Sim(C0,Cj)进行归一化处理,归一化公式为
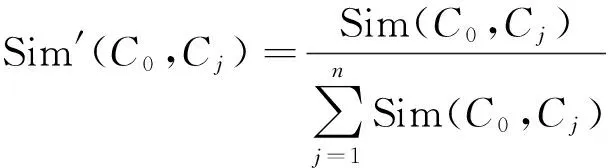
(8)
2.2案例的问题与解决方案间的关系分析
决策者通过借鉴历史案例生成目标案例的解决方案,因此,一个很自然的想法就是分析历史案例的问题与解决方案之间的关系,然后通过关联关系生成应急方案.目前求解关联度的方法主要有余弦向量和灰色关联度.灰色关联度法需要确定各项指标的最优值,主观性过强,同时部分指标最优值难以确定;而向量余弦度量法是一种客观的方法,更适用于衡量问题与解决方案属性间的关联,目前广泛应用于文本挖掘中的文件比较[23],文献[24]应用向量余弦进行了方案的比较.向量余弦的定义如下.
定义2设向量U=(u1,u2,…,ue),V=(v1,v2,…,ve),则其夹角余弦为
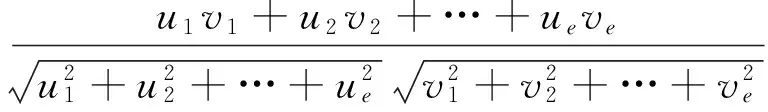
(9)
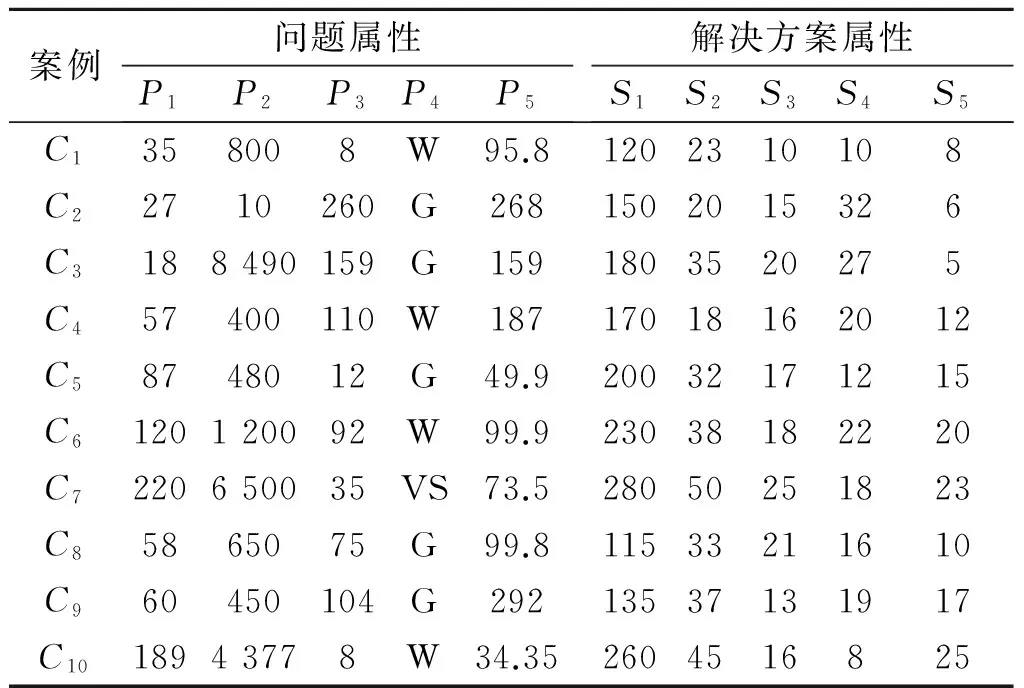
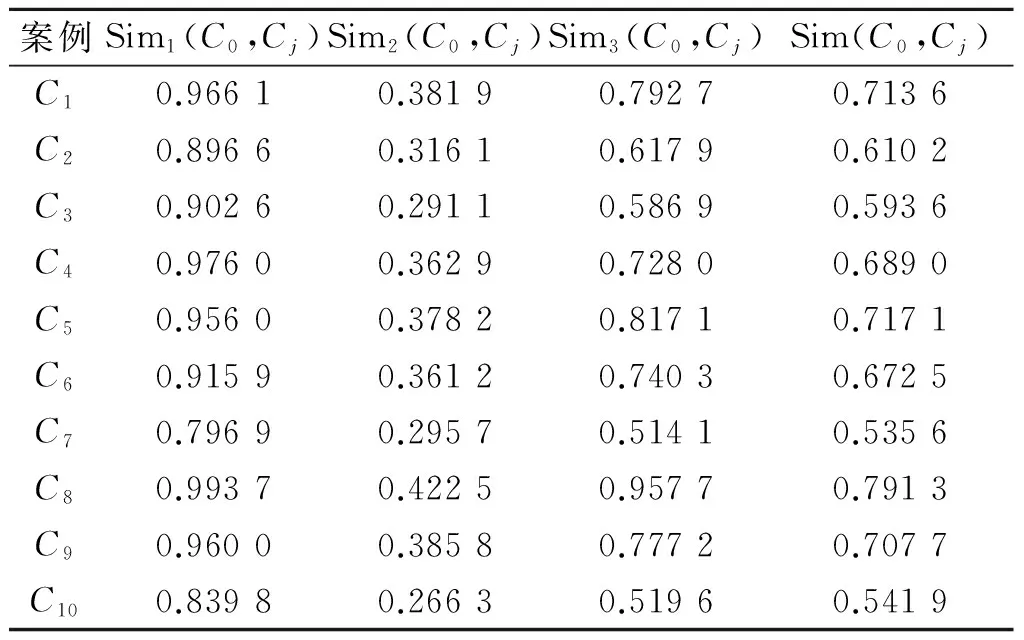
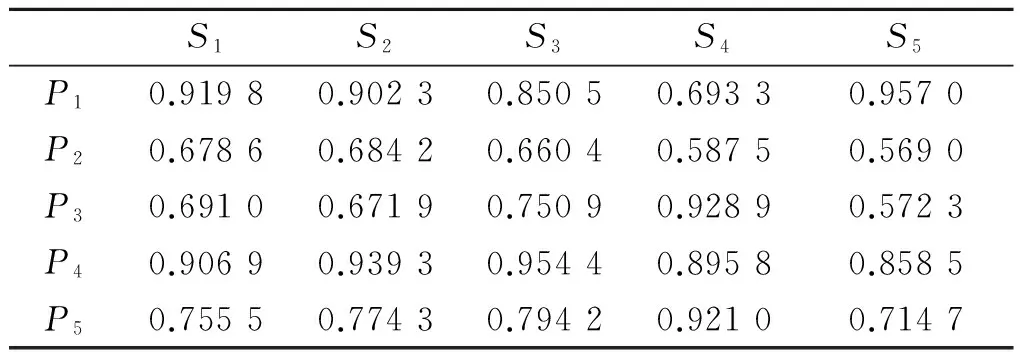
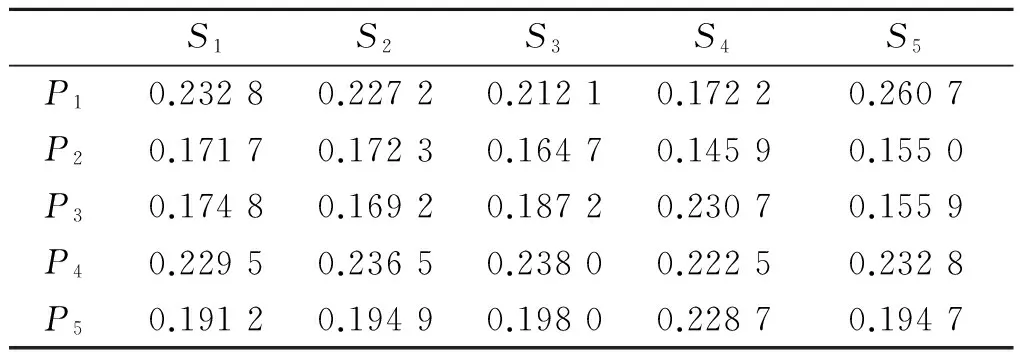
显然,因为对属性的取值都大于或等于0,所以夹角余弦0 , (10) 为避免结果失真,需要对关联矩阵[zlt]进行归一化处理,归一化公式为 (11) 2.3案例调整 王应明[24]指出,夹角余弦的大小只反映向量X和Y之间的方向,不反映向量模的大小.由此可见,利用夹角余弦表示2个向量之间的关系,除了考虑向量之间的夹角余弦大小之外,还必须考虑向量模的大小.因此,在计算目标案例的解决方案属性值时,还必须考虑历史案例的问题属性模与解决方案属性的模.历史案例的问题属性与解的属性模的计算公式分别为: (12) (13) 在此基础上,计算目标案例的解决方案属性,计算公式为: (14) 由公式(14)可知,y0t的结果与历史案例的问题与解决方案属性间的向量余弦夹角、问题的模、解决方案的模以及当前的突发事件的问题属性紧密相关. 综上所述,根据历史案例,将求解目标案例的解决方案的计算步骤归纳如下: 步骤1根据模型(6)确定属性权重wl;依据式(1)~(5)和(7),计算目标案例C0与历史案例Cj的综合案例相似度Sim(C0,Cj),并根据式(8)进行归一化处理,得到Sim′(C0,Cj); 步骤2对历史案例的问题与解决方案的属性都乘以Sim′(C0,Cj),然后,依据式(9)计算问题与解决方案属性之间的余弦夹角; 步骤3依据式(11)对问题与解决方案属性之间的余弦关系进行归一化; 步骤4依据式(12)和(13),求解案例的问题属性与解决方案属性的模; 步骤5依据式(14)求解目标案例的解决方案. 考虑高层建筑火灾的应急方案生成问题.某天某座高层建筑发生火灾,当前的情形是伤亡人数(P1)为53人,燃烧面积(P2)为680 m2,着火高度(P3)为60 m,该建筑的室内固定消防能力(P4)一般,该建筑的高度(P5)为95 m.对于高层建筑火灾出动的警力主要包括消防人员(S1,单位:人),水罐炮车(S2,单位:辆),中高压泵消防车(S3,单位:辆),高喷车(S4,单位:辆)和抢险救援车(S5,单位:辆).目前,收集到10个与当前火灾同类型的历史高层建筑火灾案例(C1,C2,…,C10),其问题与解决方案属性信息见表2.其中,固定消防能力水平的语言评价等级分别为极差(VW),差(W),一般(G),强(S)和非常强(VS).下面给出应急方案生成过程的部分计算过程,并与只根据检索结果得到的传统解决方案进行比较. 表2 问题与解的属性值信息 首先,将表2中的固定消防能力水平作为语言变量,根据定义1,将其转换为三角函数,结果为(VW,W,G,S,VS)=((0,0,0.25),(0,0.25,0.5),(0.25,0.5,0.75),(0.5,0.75,1),(0.75,1,1)),并根据重心去模法得到精确数(VW,W,G,S,VS)=(0.083 3,0.25,0.5,0.75,0.916 7). 表3 3种案例相似度及其平均相似度 其次,根据式(8)对综合案例相似度进行归一化处理得到Sim′(C0,Cj),并将历史案例的问题与解的属性都乘以Sim′(C0,Cj),在此基础上,依据式(9)计算目标案例的问题与解属性之间的余弦夹角,计算结果见表4. 表4 问题与解决方案间属性余弦夹角 然后,依据式(11)对问题与解的属性余弦夹角进行归一化处理,其计算结果见表5. 表5 标准化的问题与解属性余弦夹角 最后,依据式(14)求出目标问题的解,其计算结果为y01=112.734 2,y02=20.762 3,y03=10.825 9,y04=12.053 9,y05=9.301 1.根据问题的实际情况,需要对属性求上限值,所以得到解的向量为(113, 21, 11, 13, 10). 若按传统方法,单纯地根据检索结果获取目标案例的解决方案,那么,由表3可知,与目标案例最相似的案例为C8,其解决方案属性向量为(115, 33, 21,16, 10).显然,与得到的解决方案存在一定的差异.从表2的原始数据可以得到,案例C8的伤亡人数、着火高度与建筑高度的情况都比目标案例C0恶劣,案例C8的燃烧面积比目标案例C0略小,案例C8的固定消防能力水平与目标案例C0相同.而且从表5可以得到,伤亡人数、着火高度与建筑高度的属性与解决方案的属性向量余弦夹角都大于固定消防能力水平与解决方法的向量余弦夹角,说明决策者在制定决策方案时,考虑伤亡人数、着火高度与建筑高度的变化情况与解决方案的属性变化情况更为一致.因此,可以认定案例C8的情况比目标案例C0恶劣,若单纯根据检索结果采用案例C8的解决方案,势必造成物力人力的浪费.本文根据问题与解决方案之间的关系得到解决方案,更符合实际情况. 案例推理是对人类解决问题方式的一种直观模拟,在解决半结构化和非结构化的决策问题时具有较大的优越性,并且其解决方案很容易被决策者采纳,因而在很多领域受到了决策者的青睐.案例推理中的关键步骤是检索和调整.目前,对于案例检索方法的研究已经比较成熟,但是对于案例调整的研究还比较匮乏.本文基于研究案例的问题与解决方案之间的关系,对目标案例的方案进行了调整.主要思想是通过向量余弦夹角确定问题属性与解决方案属性之间的关系,并依据这种关系得到当前问题的解决方案.基于问题与解关系的案例调整方法较于传统方法更客观,算例亦说明了其有效性和可行性. [1]LIUY,FANZP,ZHANGY.Riskdecisionanalysisinemergencyresponse:Amethodbasedoncumulativeprospecttheory[J]. Computers & Operations Research,2014,42:75-82. [2]LIU Y, FAN Z P, YUAN Y, et al. A FTA-based method for risk decision-making in emergency response[J]. Computers & Operations Research,2014,42:49-57. [3]YANG J, XU C. Emergency decision engineering model based on sequential games[J]. Systems Engineering Procedia,2012(5):276-282. [4]YU L, LAI K K. A distance-based group decision-making methodology for multi-person multi-criteria emergency decision support[J]. Decision Support Systems,2011,51(2):307-315. [5]FAN Z P, LI Y H, WANG X, et al. Hybrid similarity measure for case retrieval in CBR and its application to emergency response towards gas explosion[J]. Expert Systems with Applications,2014,41(5):2526-2534. [6]陈兴,王勇,吴凌云,等.多阶段多目标多部门应急决策模型[J].系统工程理论与实践,2010(11):1977-1985. CHEN Xing, WANG Yong, WU Lingyun, et al. Emergency decision model with multiple stages, multiple objectives, and multidivisional cooperation[J]. System Engineering-Theory & Practice,2010,30(11):1977-1985. [7]LIAO Z, MAO X, HANNAM P M, et al. Adaptation methodology of CBR for environmental emergency preparedness system based on an improved genetic algorithm[J]. Expert Systems with Applications,2012,39(8):7029-7040. [8]HUANG C, SHEN S, HUANG Q. An approach of information processing for CBR in emergency management engineering[J]. Systems Engineering Procedia,2012(5):185-190. [9]LIU W, HU G, LI J. Emergency resources demand prediction using case-based reasoning[J]. Safety Science,2012,50(3):530-534. [10]QI J, HU J, PENG Y. A new adaptation method based on adaptability underk-nearest neighbors for case adaptation in case-based design[J]. Expert Systems with Applications,2012,39(7):6485-6502. [11]HU J, QI J, PENG Y. New CBR adaptation method combining with problem-solution relational analysis for mechanical design[J]. Computers in Industry,2015,66:41-51. [12]FUCHS B, LIEBER J, MILLE A, et al. Differential adaptation: An operational approach to adaptation for solving numerical problems with CBR[J]. Knowledge-Based Systems,2014,68:103-114. [13]JUNG S, LIM T, KIM D. Integrating radial basis function networks with case-based reasoning for product design[J]. Expert Systems with Applications,2009,36(3):5695-5701. [14]SHARIFI M, NAGHIBZADEH M, ROUHANI M. Adaptive case-based reasoning using support vector regression[C]//Advance Computing Conference (IACC), 2013 IEEE 3rd International. Ghaziabad: IEEE,2013:1006-1010. [15]LI H, SUN J. Majority voting combination of multiple case-based reasoning for financial distress prediction[J]. Expert Systems with Applications,2009,36(3):4363-4373. [16]ZHANG S. Nearest neighbor selection for iteratively KNN imputation[J]. Journal of Systems and Software,2012,85(11):2541-2552. [17]LI H, SUN J. Gaussian case-based reasoning for business failure prediction with empirical data in China[J]. Information Sciences,2009,179(1):89-108. [18]LI H, SUN J, SUN B L. Financial distress prediction based on OR-CBR in the principle ofk-nearest neighbors[J]. Expert Systems with Applications,2009,36(1):643-659. [19]LIU H, CHEN W, KANG Z, et al. Fuzzy multiple attribute decision making for evaluating aggregate risk in green manufacturing[J]. Tsinghua Science & Technology,2005,10(5):627-632. [20]ZHAO K, YU X. A case based reasoning approach on supplier selection in petroleum enterprises[J]. Expert Systems with Applications,2011,38(6):6839-6847. [21]GU D X, LIANG C Y, BICHINDARITZ I, et al. A case-based knowledge system for safety evaluation decision making of thermal power plants[J]. Knowledge-Based Systems,2012,26:185-195. [22]YAN A, SHAO H, GUO Z. Weight optimization for case-based reasoning using membrane computing[J]. Information Sciences,2014,287:109-120. [23]付永贵.基于云计算的余弦向量度量法文本检索模型[J].情报科学,2012,30(5):736-739. FU Yonggui. The cosine vector measuring method text retrieval model based on cloud computing[J]. Information Science,2012,30(5):736-739. [24]王应明.一种多指标决策与评价的方法-投影法[J].统计与研究,1998(4):66-69. WANG Yingming. A method for multi indicies decision and evaluation:A projection method[J]. Statistical Research,1998(4):66-69. A case adaptation method based on problem-solution relation for emergency decision making. ZHENG Jing1,2, WANG Yingming1, CHEN Shengqun2 (1.DecisionSciencesInstitute,FuzhouUniversity,Fuzhou350116,China; 2.CollegeofElectronicsandInformationScience,FujianJiangxiaUniversity,Fuzhou350108,China) This paper proposes a decision analysis method based on the problem-solution relation of similar cases to support the emergency alternative adaptation. The overall similarity between the target case and historical cases can be calculated by adopting a hybrid approach, it is then integrated into the attributes of historical cases’ problem and solution, relation of historical cases’, we can estimate the relation between the problem and solution based on their cosine angle. The adaptation of the emergency alternative should take accout not only on the angle relation between the problem and the solution, but also the size of the module. Finally, a numerical example is provided to illustrate the feasibility and validity of the proposed emergency case adaptation method based on the problem-solution relation. case-based reasoning; emergency decision making; case adaptation; cosine angle 2015-08-31. 国家杰出青年科学基金(70925004);福建省教育厅科技项目(JB14122);福建江夏学院青年科研人才培育基金项目(JXZ2014009);福建省自然科学基金资助项目(2015J01279). 郑晶(1980-),ORCID:http://orcid.org/0000-0002-2785-0342,女,博士,副教授,主要从事决策理论与方法研究. ,ORCID:http://orcid.org/0000-0002-5229-0914,E-mail:msymwang@hotmail.com. 10.3785/j.issn.1008-9497.2016.05.012 C 931 A 1008-9497(2016)05-560-07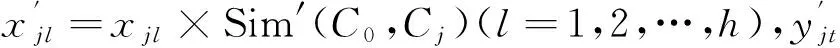
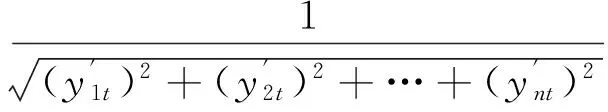

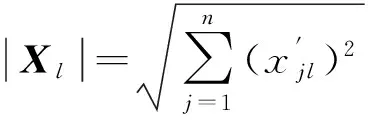
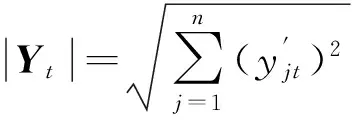
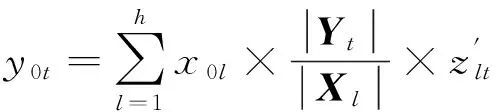
3 算 例
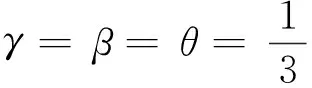
4 结 论


