阴影匹配/粒子滤波自适应加权组合定位算法

胡　辉，欧敏辉，颜瑜军

(华东交通大学信息工程学院，江西 南昌　330013)



阴影匹配/粒子滤波自适应加权组合定位算法

胡辉，欧敏辉，颜瑜军

(华东交通大学信息工程学院，江西 南昌330013)

针对城市峡谷场景中，传统阴影匹配定位算法只能提高过街定位精度，不能提高沿街定位精度问题，基于粒子滤波定位算法定位精度的分布特点，提出了阴影匹配/粒子滤波自适应加权组合定位算法。该算法根据阴影匹配运动状态下定位驻留时间特性和模板分值统计特性，计算自适应加权因子，对阴影匹配和粒子滤波定位算法进行自适应加权，得到最终定位结果。试验结果表明：该算法与阴影匹配、粒子滤波、阴影匹配/卡尔曼滤波组合、阴影匹配/粒子滤波组合定位算法相比，分别在沿街方向平均误差从5.04 m缩小到2.80 m，在过街方向平均误差从4.87 m缩小到1.30 m，均方根误差从6.82 m缩小到3.47 m。

阴影匹配；粒子滤波；自适应加权；定位精度

0　引言

城市峡谷是一种高楼密集、高楼间距离短的城市环境，道路上空的可视卫星分布在与道路平行的“条状”天空中，导致误差放大因子GDOP(Geometric Dilution of Precision)值一般都大于几十，使得在此场景中GPS存在较大的定位误差。在城市峡谷中，由于环境复杂，建筑物对卫星信号的阻碍，以及行人和车辆对卫星信号造成衰减，需要更好的方法进行GPS定位处理提高定位精度。国内外学者研究将粒子滤波PF(Particle filter)算法应用于GPS传统伪距定位解算的优化，粒子滤波技术是利用统计学特性进行建模，可以较好地解决模型上因近似非线性所带来的主观性误差，随着采样粒子数的增大，逐渐趋向状态的后验概率密度，在GPS动态单点、高动态等导航定位数据处理中获得了广泛应用，比传统最小二乘和卡尔曼滤波具有更高的定位精度[1-4]。在城市峡谷环境，由于建筑物的遮挡，过街方向的卫星信号是阻碍的，这使得在过街方向的定位精度很差。然而在沿街方向卫星信号是无阻碍的，利用非线性最优估计算法优化GPS的定位精度在沿街方向比过街方向更接近真实值[5]。此外，Groves提出了在城市峡谷场景一种新的提高定位精度的阴影匹配算法SM(Shadow matching)，该算法了利用卫星可见性判断来实现定位，在真实场景静态实验验证过街方向可达到米级定位精度[6]；随后L.Wang针对阴影匹配打分模板进行改进，新的模板与传统模板相比，过街方向误差减少了9.4%[7-8]；L.Wang在2014年应用非线性算法阴影匹配/卡尔曼滤波、阴影匹配/粒子滤波组合算法实现定位，新的算法在过街方向达到2 m精度的概率是72.4%[9]。但是，阴影匹配只能提高过街方向的定位精度，却不能提高沿街方向的定位精度。本文针对此问题，提出了阴影匹配/粒子滤波自适应加权组合定位算法。

1　粒子滤波及阴影匹配算法

1.1粒子滤波算法

粒子滤波算法基本步骤包括：初始化、重要性权值计算、权值归一化、重采样以及输出。

(1)

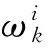
(2)

步骤三：权值归一化

(3)

步骤四：重采样。采用系统重采样算法，权值较大的样本被多次复制，权值较小的样本则可能会被剔除。

步骤五：输出。系统状态的最小均方误差估计

(4)

令k=k+1，返回步骤二。

1.2阴影匹配算法

阴影匹配算法原理是根据卫星信号被建筑物遮挡情况判断接收机位置。通过建立的建筑物轮廓模型数据和卫星星历，预测城市峡谷中候选位置处的卫星可见性，与实际该候选位置接收到卫星信号的可见性进行比较。依照打分模板，当预测和实际观测卫星都不可见或预测和实际观测卫星都可见，则给定分值1。当预测卫星不可见，而实际观测可见或预测卫星可见，而实际观测不可见，则给定分值0。对于每个候选位置的打分函数如下：

(5)

式(5)中，fpos,k(j)是j候选位置在k时刻最终的分值；fsat,k(i,j)是k时刻第i颗卫星在候选位置点j处使用打分模板得到的分值，综合考虑到系统对算法精度和速度的要求，选定候选位置网格点Nsm=600。仿真数据显示k时刻对应的候选位置打分分值分布如图1。

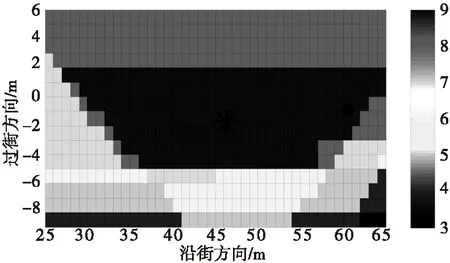
图1　阴影匹配候选位置分值分布图Fig.1　The score distribution of candidate location of the Shadow matching

图1中深色对应的高分值候选位置，可看出有很多高分值候选位置，这些高分值候选点认为是近邻关系，因此使用类似K-NN(k-nearestneighbours)算法来估计最终位置。对于L个高分值区域，阴影匹配定位结果如图用“*”表示，公式为：

(6)

(7)

其中，xsme,k，xsmn,k对应的是k时刻使用阴影匹配定位算法在沿街和过街的定位位置。ei,k和ni,k分别对应的是k时刻第i个高分值候选位置的沿街、过街位置。

2　阴影匹配/粒子滤波自适应加权组合定位算法

将粒子滤波应用于GPS定位解算中，首要是建立状态模型和观测模型。定义xpf,k为系统状态向量，zk为系统观测向量。

xpf,k=[xpfe,k,vpfe,k,xpfn,k,vpfn,k]T

(8)

zk=[ze,k,zn,k,vk,θk]T

(9)

式中系统状态向量由粒子滤波优化GPS数据在k时刻的沿街、过街位置xpfe,k,xpfn,k和沿街、过街速度vpfe,k,vpfn,k构成，观测向量由GPS输出经转换矩阵转换在k时刻的沿街、过街位置ze,k,zn,k，速度vk和方位角θk构成。

2.1系统状态方程

本文以PV(Position，Velocity)模型来模拟接收机在城市峡谷场景的运动状态。状态量包括沿街、过街位置、速度、方位角。其中每个方向上的位置和速度所含噪声是相互独立的，相关系数为0。系统的状态转移方程为：

xpf,k=Φkxpf,k-1

(10)

其中

(11)

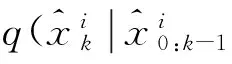
2.2系统观测方程

系统的观测方程，沿街位置和过街位置和系统状态参数的关系为：

ze,k=xpfe,k+εe,k

(12)

zn,k=xpfn,k+εn,k

(13)

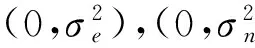
(14)

(15)

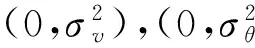
(16)

2.3自适应加权因子αk,βk的计算

该算法根据阴影匹配运动状态下定位驻留时间特性和模板分值统计特性，计算自适应加权因子。本文中设定阴影匹配过街和粒子滤波算法沿街具有相同的加权因子，这充分利用阴影匹配过街定位精度和粒子滤波优化GPS沿街定位精度的优势，加权组合模型如下式：

xe,k=αkxsme,k+βkxpfe,k

(17)

xn,k=βkxsmn,k+αkxpfn,k

(18)

式(17)(18)中xe,k、xn,k为k时刻输出最终沿街、过街定位结果，xpfe,k、xpfn,k为k时刻经粒子滤波优化GPS定位算法输出结果，αk,βk分别为对阴影匹配和粒子滤波沿街和过街的加权因子。在城市峡谷环境中，由于建筑物轮廓信息变化不明显，使得卫星在候选位置点的定位可见性变化不明显，阴影匹配运动状态下在同一位置定位驻留一定时间，定位驻留时间tsm,k越大，造成定位误差越大。同时，从图1中也可以看出，符号“•”对应真实位置，符号“*”对应阴影匹配定位位置，可见通过模板分值统计高分值候选位置数目hsm,k越大，阴影匹配定位误差也就越大。因此本文建立基于tsm,k，hsm,k的自适应因子αk,βk计算，用来充分利用粒子滤波沿街精度和阴影匹配过街精度，如下：

(19)

βk=1-ak

(20)

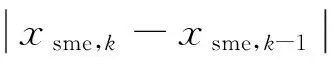
3　试验结果与分析

本文实验在华东交通大学15与16栋之间峡谷场景，实验路径如图2(左)中A-B所示，初始位置A坐标为(28°44′52.178 75″N,115°51′41.745 64″E,45.25m)，终止位置B坐标(28°44′52.722 85″N,115°51′43.545 70″E,45.12m)，AB距离为83.27m。其中峡谷宽度为15m，峡谷长度为50m，实景图如图2(右)；通过4台南方S82RTK进行静态联测，获取精确基准点A和B坐标，架设徕卡TS06全站仪在基准点A上测量A点到B点参考路线基本信息；在基准点A和B上，利用全站仪测量建筑物各个特征顶点的坐标，建立建筑物轮廓模型；使用更新率为1Hz的SuperstarIIGPS接收机在2015年5月11日17:35:07～17:36:41采集实验数据。

图2　城市峡谷路线A-B和实景图Fig.2　The route A-B and scenario of the urban canyon

图3是SuperstarII接收机在沿街、过街定位误差结果。GPS接收机在38～80s之间沿街、过街都存在较大误差，沿街方向最大误差为6.5m，而过街方向最大误差为13m。在城市峡谷场景中，GPS接收机在沿街方向的定位精度优于过街方向。

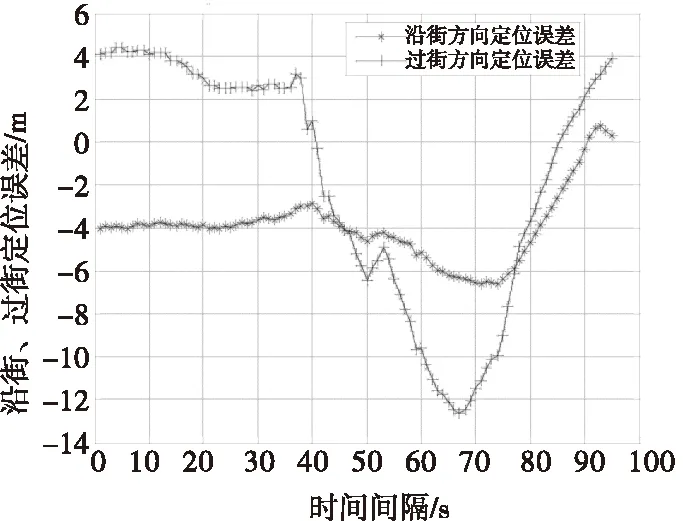
图3　SuperstarII在沿街、过街方向定位误差Fig.3　The positioning error of the along-street and cross-street measured by superstarII

3.1阴影匹配定位结果和阴影匹配定位特性

图4阴影匹配沿街方向定位结果呈齿状，是由于卫星短时间内星空分布不变，且建筑物边缘轮廓信息变化不明显，使得阴影匹配运动状态下定位同一位置驻留一定时间。图中看出沿街最大定位误差16m，尤其在36～69s之间，输出同一位置持续时间达33s，造成大的定位误差。从图4看出阴影匹配定位算法在过街方向有较高定位精度，最大误差2.4m。

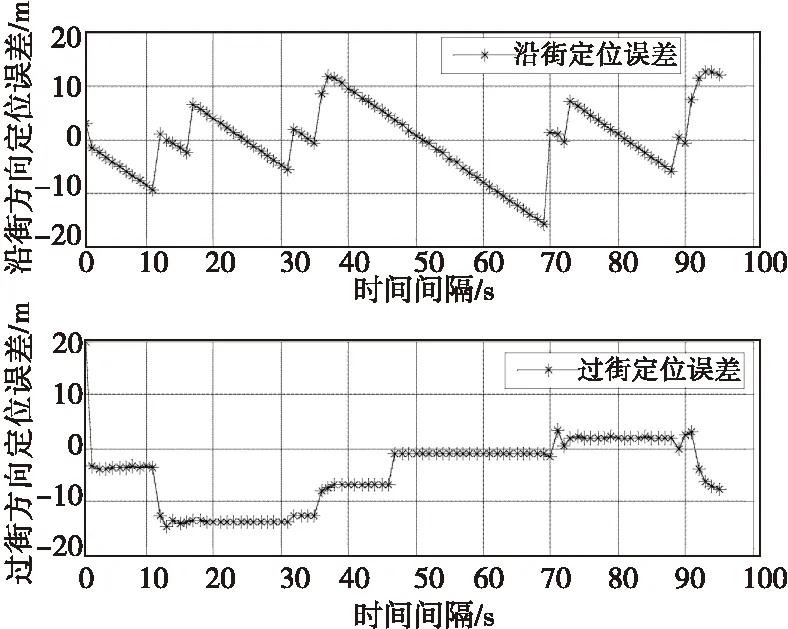
图4　阴影匹配沿街、过街定位结果Fig.4　The along-street and cross-street positioning results of the shadow matching

从图5看出，阴影匹配运动状态下只在11个位置处存在定位结果，根据式(19)中tsm,k在一定时间内持续增大，在37m处，tsm,k最大达33s，产生大的定位误差。模板分值统计高分值候选位置数目，在47～69s间，hsm,k数目达到210个，对应数目越大，定位误差也越大。根据式(19)、式(20)驻留时间tsm,k和高分值候选位置数目hsm,k可以计算αk，βk值，当tsm,k和hsm,k增大，对应αk逐渐变小，此时阴影匹配沿街定位误差大，而βk逐渐增大，充分利用粒子滤波优化GPS的沿街定位精度和阴影匹配的过街定位精度。

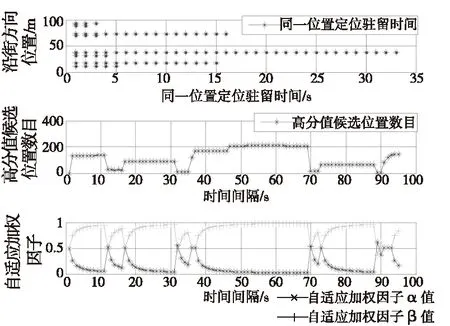
图5　阴影匹配动态下定位驻留时间、高分值候选位置数目、自适应加权因子Fig.5　The lingering time of shadow matching under dynamic positioning， number of candidate locations of high scores， adaptive weighted factors

3.2算法性能比较

图6—图9为阴影匹配粒子滤波自适应加权组合定位算法与几种算法的性能比较结果。

从图6可以看出，该方法相比阴影匹配算法，从即将进入峡谷、峡谷中、出峡谷沿街方向都具有良好的定位精度，在过街方向，该方法比阴影匹配定位精度高，峡谷中仅在70s附近存在一定偏差，当快速收敛到真实位置附近；从图7可以看出，该方法相比粒子滤波算法，在峡谷外和峡谷内，沿街方向都比粒子滤波定位精度高或保持同粒子滤波相同定位精度，在过街方向，可以明显看出该方法比粒子滤波定位精度高很多；从图8可以看出，该方法与阴影匹配/卡尔曼组合算法相比，在沿街方向存在较高的定位精度，在过街方向基本上精度更好，仅存在部分点有3m左右偏差；从图9可以看出，该方法与阴影匹配/粒子滤波组合算法相比，在沿街方向存在较高定位精度，在过街方向也基本上存在较高的定位的精度，仅部分点位置有3m左右偏差。从这几个图能够看出该算法具有很高的定位精度，详细性能比较见表1。

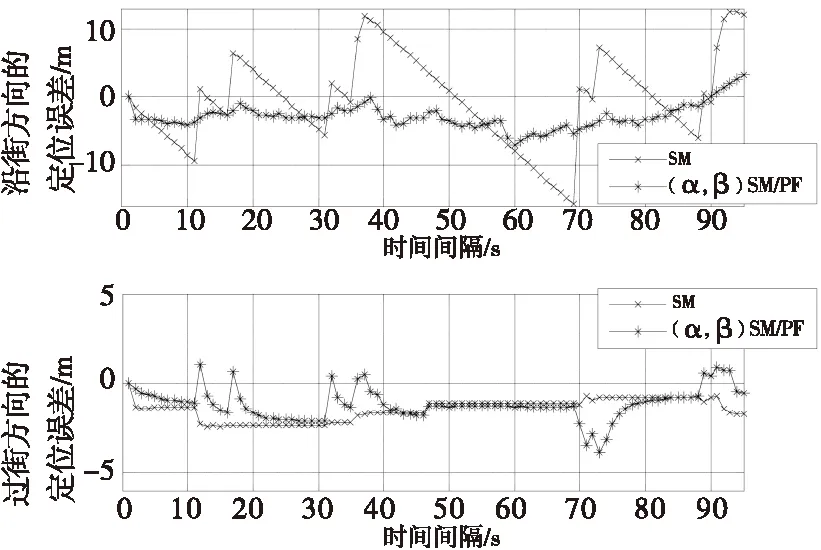
图6　该算法与阴影匹配算法的比较Fig.6　The algorithm was compared with the Shadow matching algorithm

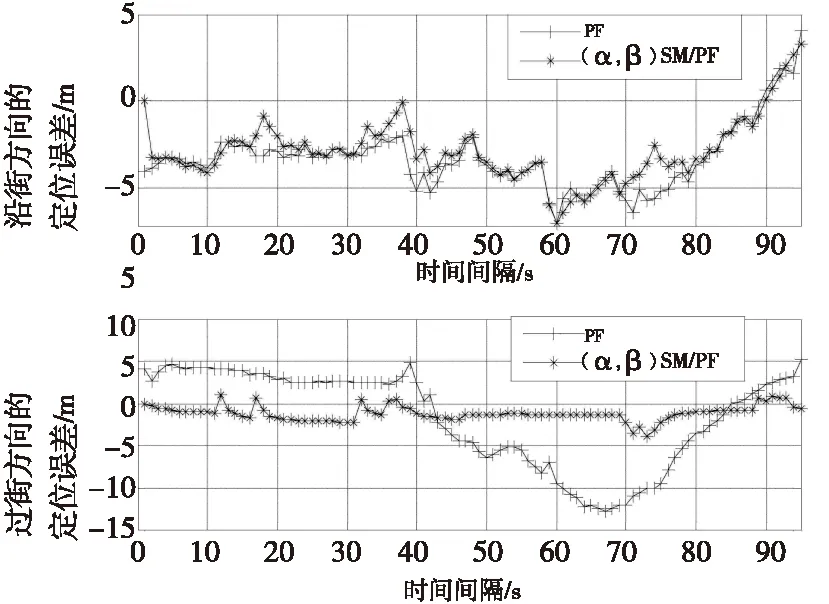
图7　该算法与粒子滤波算法的比较Fig.7　The algorithm was compared with the Particle filter algorithm

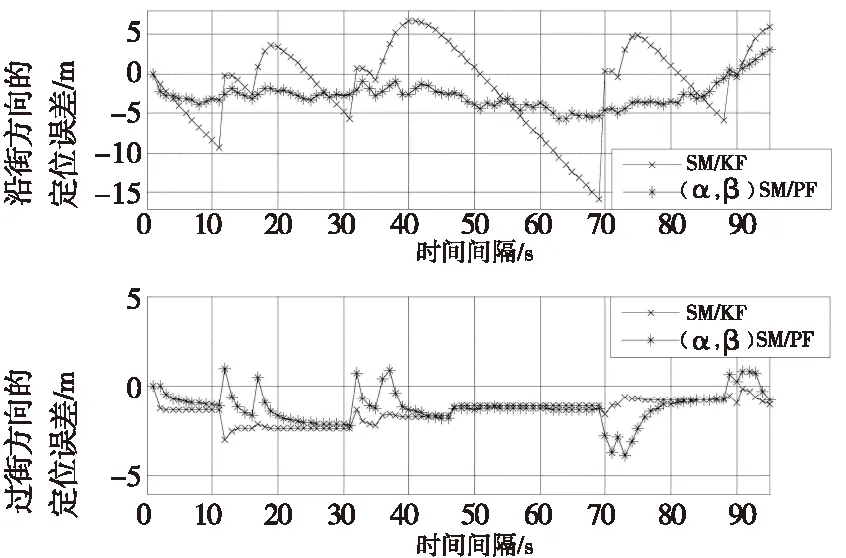
图8　该算法与阴影匹配/卡尔曼组合算法的比较Fig.8　The algorithm combined with Shadow match/Kalman algorithm

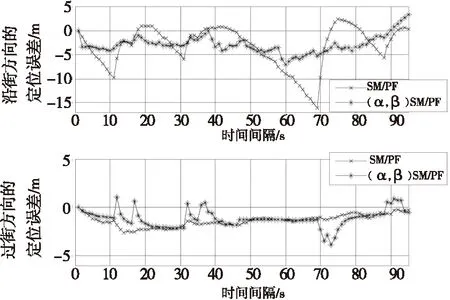
图9　该算法与阴影匹配/粒子滤波组合算法的比较Fig.9　The algorithm is compared with Shadow matching/Particle filter algorithm

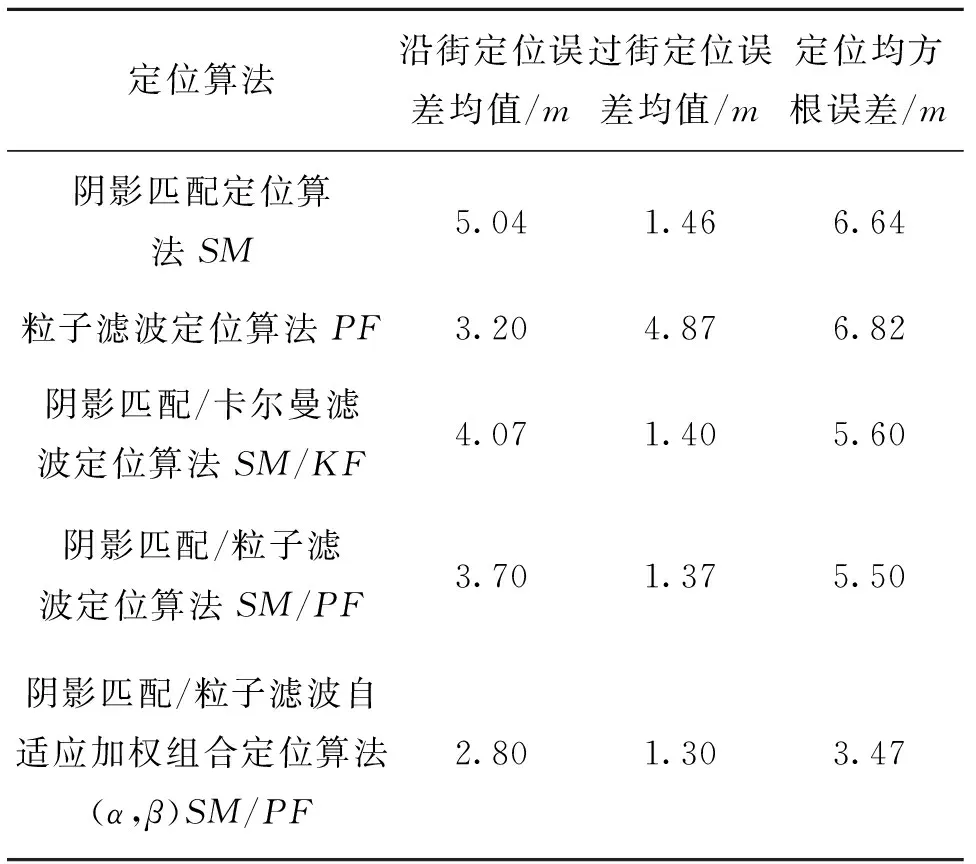
定位算法沿街定位误差均值/m过街定位误差均值/m定位均方根误差/m阴影匹配定位算法SM5.041.466.64粒子滤波定位算法PF3.204.876.82阴影匹配/卡尔曼滤波定位算法SM/KF4.071.405.60阴影匹配/粒子滤波定位算法SM/PF3.701.375.50阴影匹配/粒子滤波自适应加权组合定位算法(α,β)SM/PF2.801.303.47

4　结论

本文提出了阴影匹配/粒子滤波自适应加权组合定位算法，该算法根据阴影匹配运动状态下定位驻留时间特性和模板分值统计特性，计算自适应加权因子，进而对阴影匹配和粒子滤波优化GPS进行加权。实验结果表明该算法与单独使用阴影匹配算法、单独使用粒子滤波算法、阴影匹配/卡尔曼组合定位算法那、阴影匹配/粒子滤波组合定位算法相比，可以解决城市峡谷场景沿街定位精度低、不连续的问题， 同时获得过街方向定位高精度。为实现在

城市环境中基于位置服务LBS的应用提供重要参考。

[1]WangE,ZhaoW,CaiM.ResearchonimprovingaccuracyofGPSpositioningbasedonparticlefilter[C]//IndustrialElectronicsandApplications(ICIEA), 2013 8thIEEEConferenceonIEEE, 2013:1167-1171.

[2]王尔申,蔡明,庞涛.MCMC粒子滤波的GPS定位数据处理算法[J]. 数据采集与处理,2013(2):213-218.

[3]王尔申,庞涛,李兴凯,等. 基于遗传算法和神经网络的改进粒子滤波的GPS定位数据处理[J]. 电子器件,2015(2):410-413.

[4]王尔申,庞涛,李兴凯,等. 基于遗传粒子滤波的GPS定位数据处理算法[J]. 太赫兹科学与电子信息学报,2015(3):419-422.

[5]WangL,GrovesPD,ZiebartMK.GNSSShadowMatching:ImprovingUrbanPositioningAccuracyUsinga3DCityModelwithOptimizedVisibilityScoringScheme[J].Navigation, 2013, 60(3):195-207.

[6]GrovesPD,WangL,WalterD,etal.TheFourKeyChallengesofAdvancedMultisensorNavigationandPositioning[C]//Position,LocationandNavigationSymposium-PLANS2014, 2014IEEE/ION.US:IEEE, 2014:773-792.

[7]WangL,GrovesP,ZiebartM,etal.UrbanPositioningonaSmartphone:Real-timeShadowMatchingUsingGNSSand3DCityModels[J].ProceedingsofInternationalTechnicalMeetingoftheSatelliteDivisionoftheInstituteofNavigation, 2013:1606-1619.

[8]WangL,GrovesPD,ZiebartMK.SmartphoneShadowMatchingforBetterCross-streetGNSSPositioninginUrbanEnvironments[J].JournalofNavigation, 2015, 68:411-433.

[9]WangLei.KinematicGNSSShadowMatchingUsingaParticleFilter[C]//Proceedingsofthe27thInternationalTechnicalMeetingofTheSatelliteDivisionoftheInstituteofNavigation.Tampa,Florida, 2014:1907-1919.

[10]SunZ,MaoX,TianW,etal.Activityclassificationanddeadreckoningforpedestriannavigationwithwearablesensors[J].MeasurementScience&Technology, 2009, 20(1):187-188.

Shadow Matching/Particle Filter Adaptive Weighted Integrated Localization Algorithm

HU Hui，OU Minhui，YAN Yujun

(College of Information Engineering，East China Jiaotong University，Nanchang 330013，China)

Traditional shadow matching localization algorithm could only improve the cross-street positioning accuracy in urban canyon, and could not improve the along-street accuracy. A shadow matching/particle filter adaptive weighted integrated localization algorithm based on particle filter distribution characteristics of the positioning precision was proposed in this article. According to the shadow matching positioning lingering time under motion characteristics and the statistical properties of the template score, this algorithm calculated adaptive weighted factor. Adaptive weighted shadow matching and particle filter positioning algorithm could get the final localization results. Experimental results showed that the proposed algorithm, compared with shadow matching, particle filter, shadow match/Kalman algorithm , shadow matching/particle filter, could decreased average along-street, error from 5.04 m to 2.80 m decreased average cross-street error from 4.87 m to 1.30 m, decreased the root-mean-square error from 6.82 m to 3.47 m.

shadow matching; particle fliter; adaptive weighted; positioning accuracy

2016-02-03

江西省自然科学基金项目资助(20142BAB207001)；江西省教育厅科学技术研究项目资助(GJJ14369)

胡辉(1970—)，男，江西南昌人，博士，教授，研究方向：卫星导航定位，并行算法与分析处理，机器视觉。E-mail:gnss523@163.com。

TN961

A

1008-1194(2016)04-0082-06