信号重构中测量矩阵性能的判据
程 涛
(1. 深圳大学光电工程学院,光电子器件与系统重点实验室,广东 深圳 518060;2. 广西科技大学汽车与交通学院,广西 柳州 545006;3.深圳大学光电工程学院,深圳生物医学光学微纳检测与成像重点实验室,广东 深圳 518060)
信号重构中测量矩阵性能的判据
程涛1,2,3
(1. 深圳大学光电工程学院,光电子器件与系统重点实验室,广东 深圳518060;2. 广西科技大学汽车与交通学院,广西 柳州545006;3.深圳大学光电工程学院,深圳生物医学光学微纳检测与成像重点实验室,广东 深圳518060)
针对压缩感知中测量矩阵性能判据混乱的问题,提出基于不同类型重构算法的测量矩阵性能判据。该判据比传统方法的可操作性更好,在矩阵的其他性质都近乎一致的条件下实现了对具有不同列不相关性矩阵的严格对比实验。实验结果表明,对于OMP(orthogonal matching pursuit)算法,测量矩阵的列不相关性可作为测量矩阵性能判据,但当列不相关性达到一定程度(即μcmax>0.25)后对测量矩阵性能再无影响。对于BP(Basis Pursuit)算法,具有相同解空间的测量矩阵性能与列不相关性无关;测量矩阵的列不相关性不是判断测量矩阵性能的主要判据。一个矩阵能达到的理论上限就是等规模的哈达玛矩阵的重构能力。
压缩感知;测量矩阵;信号;相关性;解空间
0 引言
信息技术的飞速发展使得获取和利用海量数据和信号成为可能。信号的数字化是通过从模拟信源采样实现的。但是,奈奎斯特采样定理指出,带限信号的采样频率必须大于其带宽的两倍以上才能确保由采样完全重构原始信号。只有增加信号带宽才能携带更多的信息。但是信号带宽的增加又导致采样频率的提高。因此,现有技术的采样频率和处理速度越来越难以与日益增长的宽带信号处理需求相匹配[1-3]。
信号中存在大量的冗余信息,人们开发了各种压缩算法,以降低存储、处理和传输的成本。压缩比大的多为损压缩方式。例如,在快速傅里叶变换中,大量不重要的高频系数被丢弃。这种前期采集大量数据,又在后期压缩过程中丢弃大量数据的格局造成了资源的严重浪费了。人们一直期望一种采集压缩一体化的信号采集处理格局。这样就可采集、传输、存储、处理和管理很少的数据,就可实现对原始信号的完全或近似重构。从而摆脱传统技术的窘境,节约巨大的人力物力资源[4]。
压缩感知就能以远低于奈奎斯特采样定理要求的频率采样,在采集信号的同时实现对信号的压缩,并能高质量地恢复原始信号。压缩感知在图像处理、视频分析、雷达遥感、信息通信、数据挖掘、军事侦察、资源探测和医学成像等领域有广阔的应用前景和巨大的经济效益[4]。压缩感知的研究内容主要分为三个部分:测量矩阵、稀疏表示和重构算法。测量矩阵主要研究测量矩阵设计、优化、性能分析等;稀疏表示主要研究信号的稀疏化方法等;重构算法主要研究压缩感知的各种求解方法。其中测量矩阵是压缩感知研究的核心。本文针对压缩感知中测量矩阵性能判据混乱的问题,提出基于不同类型重构算法的测量矩阵性能判据。
1 压缩感知理论
压缩感知理论表明,如果信号是稀疏的,就能以远低于奈奎斯特(Nyquist)采样频定理的采样率采集信号,并能以高概率精确重建稀疏信号[5],压缩感知模型如式(1)所示,求解式(1)就可以重构出稀疏信号x。
minx0s.t.y=Φx
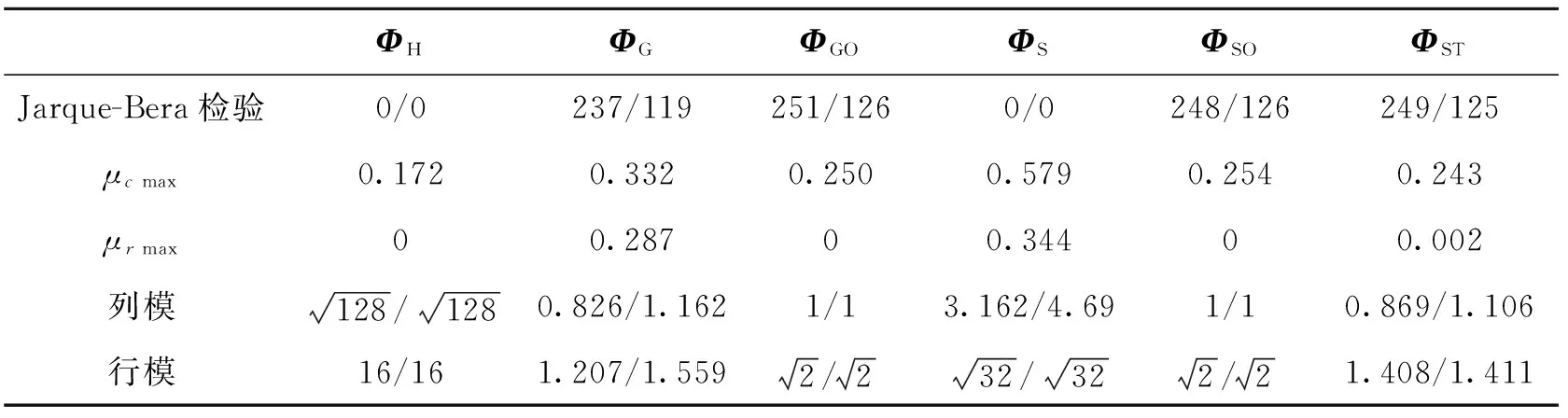
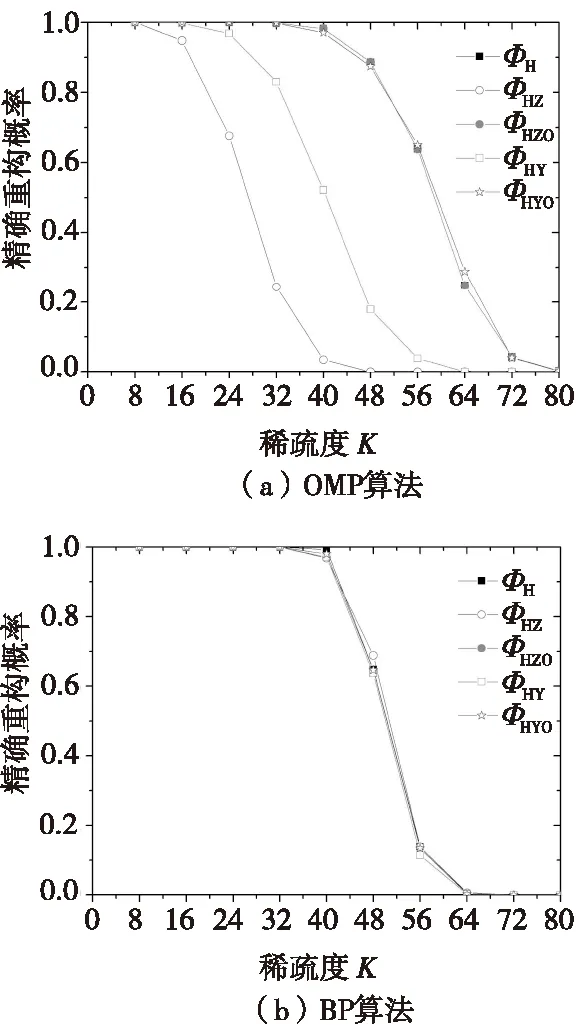
(1)式(1)中,y是测量数据,y∈RM;Φ是测量矩阵,Φ∈RM×N,M 式(1)属于非凸优化问题,缺乏完善的理论基础。因此,一般把式(1)转化成如式(2)所示的凸松弛优化问题。如果Φ满足RIP(Restricted isometry property)性质,求解式(2)就能以极高概率得到与求解式(1)一样的稀疏信号x。而且凸优化问题具有更完善的理论基础,更易于做理论分析和提高计算速度。 minx1s.t.y=Φx (2) 测量矩阵Φ的性质是关系信号重构效果的关键。当前判断测量矩阵Φ性能优劣的主要判据为是否满足RIP性质,如式(3)所示[6]。但是一个矩阵及其子矩阵是否满足RIP性质的验证可操作性不强,现在只有一些定性的说明。例如,随机矩阵的RIP性质一般都较好。但是有的随机矩阵(例如,0-1随机矩阵)在式(3)中的最小和最大特征值并不是一个接近1的值。 (1-σK)x2≤Φx2≤ (3) 由于RIP的不易操作性,Donoho提出测量矩阵设计判断三原则:测量矩阵的列向量应满足一定的不相关性、测量矩阵列向量的元素应具有独立随机性、基于l1范数的解就是最优解[1]。但是这些原则也是只是基于l1范数的基础上提出的,不适用于基于l0范数的贪婪算法,例如OMP(orthogonal matching pursuit)算法。而且由于各类矩阵的各种性质都不一样,缺乏可比性,因而Donoho三原则缺乏真实对比实验的支持。 文献[1, 9—10]提出测量矩阵的行向量正交化以及列向量单位化的设计准则。文献[11—13]进一步根据哈达玛矩阵的特点,通过数学推导和证明,提出了适用于l0范数的测量矩阵设计五原则:行模相近、列模相近、各行不相关性好和各列不相关性好以及行列元素服从随机分布,并据此设计出具有不同列不相关性的高斯矩阵。但是由于文献[12]中的各种实验采用的不是同一套数据集,因而导致实验结果不是很准确,无法精确把握问题的本质。列不相关性比RIP和Donoho三原则有更好的可操作性。Elad[14]和Duarte[15]等人的矩阵设计思路也是以列相关性最小化或平均化为目标。 一般来说,测量矩阵的列不相关性越好,那么RIP性质也越好,也意味着OMP和BP的重构效果也越好。但这都是基于过去具有不同列不相关性的不同类型测量矩阵实验得到的经验性结论,并非严格意义上的对比试验。测量矩阵性能受到众多因素的影响。如果能排除测量矩阵其他各种因素的影响,就可研究清楚单一因素对测量矩阵性能的影响。然后,在这一基础上就可进一步研究其他各个因素的作用。本文设计了具有不同列不相关性的矩阵,矩阵的其他性质都近乎一致。在此基础上做对比实验,就可研究清楚列不相关性对矩阵性能的真实影响。从而确定基于不同类型重构算法的测量矩阵性能判据。 本文设计了具有不同列不相关性的哈达玛矩阵ΦH、高斯矩阵ΦG、高斯优化矩阵ΦGO、稀疏循环矩阵ΦS、稀疏循环优化矩阵ΦSO、稀疏循环近似矩阵ΦST,以及哈达玛矩阵ΦH左乘高斯方阵ΦGZ得到的ΦHZ、哈达玛矩阵左乘高斯方阵后的优化矩阵ΦHZO、哈达玛矩阵ΦH右乘高斯方阵ΦGY得到的ΦHY、哈达玛矩阵右乘高斯方阵后的优化矩阵ΦHYO。除ΦG、ΦS、ΦHZ和ΦHY之外,这些矩阵基本都满足行模相近、列模相近、各列不相关性好以及行列元素服从随机分布,如表1所示。 表1列出了测量矩阵采用哈达玛矩阵ΦH、高斯矩阵ΦG、高斯优化矩阵ΦGO、稀疏循环矩阵ΦS、稀疏循环优化矩阵ΦSO、稀疏循环近似矩阵ΦST的各种统计学参数(表1中各行数据,除“Jarque-Bera检验”外,“/”号左边的数据表示最小值,“/”号右边的数据表示最大值;“Jarque-Bera检验”行,“/”号左边的数据表示符合检验的列数,“/”号右边的数据表示符合检验的行数)。μcmax表示列间相关系数绝对值的最大值;μrmax表示行间相关系数绝对值的最大值。各类矩阵的大小都是128×256。ΦH是从元素为+1和-1的哈达玛方阵中随机抽取M行;ΦG的各元素服从N(0,1/M)分布;ΦS的初始行向量是包含32个随机分布的1的稀疏行向量,各行向量都是前一个行向量各元素依次右移2位的结果;ΦGO是采用优化算法基于ΦG得到的测量矩阵;ΦSO和ΦST是采用优化算法基于ΦS得到的测量矩阵;ΦHZ的左乘高斯方阵;ΦHZO和ΦHYO是采用优化算法基于ΦHZ和ΦHY得到的测量矩阵。其中ΦGZ的各元素服从N(0,1/M)分布,ΦGY的各元素服从N(0,1/N)分布。优化算法就是对不同的测量矩阵依次做行向量正交规范化和列向量单位化操作并循环迭代多次,以使测量矩阵的性质趋于稳定收敛。本文设定迭代次数都为100次。 OMP是基于l0范数的经典算法,BP(Basis Pursuit)是基于l1范数的经典算法。绝大多数重构算法都是在OMP和BP的基础上改进升级得到的。OMP和BP算法原理简单,不涉及信号先验信息,受信号和重构矩阵(测量矩阵)类型影响小,因而更适用于理论研究。 表1 各类矩阵的相关参数 图1—图3是采用OMP和BP两种算法重构不同稀疏度高斯信号的精确重构概率和稀疏度关系曲线。图1—图3都采用同一数据集,每种不同稀疏度的实验以不同信号重复500次。图1是哈达玛矩阵ΦH、哈达玛矩阵左乘高斯方阵ΦHZ、哈达玛矩阵左乘高斯方阵后的优化矩阵ΦHZO、哈达玛矩阵右乘高斯方阵ΦHY、哈达玛矩阵右乘高斯方阵后的优化矩阵ΦHYO的重构结果。图2是哈达玛矩阵、高斯矩阵ΦG和高斯优化矩阵ΦGO的重构结果。图3是哈达玛矩阵、稀疏循环矩阵ΦS、稀疏循环矩阵的优化矩阵ΦSO和近似矩阵ΦST的重构结果。图1—图3中的曲线ΦH都是同一条曲线。 图1 哈达玛矩阵的重构概率与稀疏度的关系Fig.1 Prob. of exact recovery vs. the sparsity by Hadamard matrices. 图2 高斯和哈达玛矩阵的重构概率与稀疏度的关系Fig.2 Prob. of exact recovery vs. the sparsity by Gauss and Hadamard matrices. 图3 稀疏循环和哈达玛矩阵的重构概率与稀疏度的关系Fig.3 Prob. of exact recovery vs. the sparsity by sparse circulant and Hadamard matrices. 根据计算结果可知,ΦHZ和ΦHZO的μc max分别为0.431和0.172;ΦHY和ΦHYO的μc max分别为0.372和0.258。ΦH的μc max分别为0.172。比较图1-图3中的图(a)可以发现,ΦHZ、ΦHY、ΦG和ΦS的列不相关性最差,而且行模和列模也不近似相等。各行列也不全服从随机分布,所以重构效果最差。ΦH、ΦHZO、ΦHYO、ΦGO、ΦSO和ΦST的μr max几乎都完全不相关,行模和列模都近似相等。尽管μc max最大为0.254,最小为0.172,相差较大,但是重构结果都几乎一样,几乎都与曲线ΦH重合。这说明,对于基于l0范数的OMP算法,测量矩阵的列不相关性达到一定程度(即μc max>0.25)就不会对信号的重构结果再产生大的影响。因此一味追求测量矩阵高的列不相关性是不合适的。这是因为OMP算法中存在最小二乘法的矩阵运算,在物理几何意义上就是平行四边形法则在高维空间的展开。只要任意两列向量间夹角大于一定程度(即μc max>0.25),就可以避免计算机中的精度不足问题,因而重构结果变化不大。 比较图1—图3中的图(b)可以发现,所有矩阵(ΦH、ΦHZ、ΦHZO、ΦHY、ΦHYO、ΦG、ΦGO、ΦS、ΦSO和ΦST)的重构曲线几乎都重合在一起。这是因为,ΦHZ、ΦHZO、ΦHY、ΦHYO、ΦGO、ΦSO和ΦST都只是相当于在ΦH、ΦG和ΦS的左边乘以一个满秩的方阵,并不会改变原方程的解空间[4, 11-12]。因此BP算法还是在原空间的可行域内做全局搜索。由此可见基于l1范数的BP算法受测量矩阵的列不相关性的影响较小。基于同一信号集,所有矩阵的任意列组的列秩几乎都是一样的,其中ΦS并不具有好的RIP性质。所以在实际操作中,好的RIP性质并不是能够取得好的重构效果的必要条件。解空间和矩阵及其子矩阵的列秩才是判断能否取得好的重构效果的必要条件。 本文提出基于不同类型重构算法的测量矩阵性能判据。基于列不相关性和解空间的判据比传统方法的可操作性更好,在矩阵的其他性质都近乎一致的条件下实现了对具有不同列不相关性矩阵的严格对比实验。实验结果表明,对于OMP(orthogonalmatchingpursuit)算法,测量矩阵的列不相关性可作为测量矩阵性能判据,但当列不相关性达到一定程度(即μc max>0.25)后对测量矩阵性能再无影响。对于BP(BasisPursuit)算法,具有相同解空间的测量矩阵性能与列不相关性无关;测量矩阵的列不相关性不是判断测量矩阵性能的主要判据。一个矩阵能达到的理论上限就是等规模的哈达玛矩阵的重构能力。拟设计更多具有不同列不相关性的测量矩阵深入探究列不相关性和解空间之间的关联和差异。 [1]DONOHODL.Compressedsensing[J].InformationTheory,IEEETransactionson, 2006, 52(4): 1289-1306. [2]戴琼海, 付长军, 季向阳. 压缩感知研究 [J]. 计算机学报, 2011, 34(3): 425-433. [3]石光明, 刘丹华, 高大化, 等. 压缩感知理论及其研究进展 [J]. 电子学报, 2009, 37(5): 1070-1081. [4]程涛. 基于压缩感知的遥感变化检测研究 [D]. 武汉: 武汉大学, 2013. [5]赵光辉, 张天键, 沈方芳, 等. 低信噪比下稳健压缩感知成像 [J]. 航空学报, 2012, 33(3): 1-10. [6]TAOC.Restrictedconformalpropertyofcompressivesensing[C]//WaveletActiveMediaTechnologyandInformationProcessing(ICCWAMTIP). 2014 11thInternationalComputerConference. 2014: 152-161. [7]WEID,MILENKOVICO.SubspacePursuitforCompressiveSensingSignalReconstruction[J].InformationTheory,IEEETransactionson, 2009, 55(5): 2230-2249. [8]CANDESEJ,TAOT.Decodingbylinearprogramming[J].InformationTheory,IEEETransactionson, 2005, 51(12): 4203-4215. [9]DONOHODL,TSAIGY,DRORII,etal.SparseSolutionofUnderdeterminedSystemsofLinearEquationsbyStagewiseOrthogonalMatchingPursuit[J].InformationTheory,IEEETransactionson, 2012, 58(2): 1094-1121. [10]CANDESEJ,TAOT.Near-OptimalSignalRecoveryFromRandomProjections:UniversalEncodingStrategies[J].InformationTheory,IEEETransactionson, 2006, 52(12): 5406-5425. [11]程涛, 朱国宾, 刘玉安. 基于0-1稀疏循环矩阵的测量矩阵分离研究 [J]. 光学学报, 2013, 33(2): 2200011-2200016. [12]程涛, 朱国宾, 刘玉安. 压缩感知中高斯矩阵的优化研究 [J]. 计算机应用研究, 2014, 31(12): 3599-3602. [13]程涛, 刘玉安. 基于单像素相机重构矩阵优化的影像采集和重构方法 [J]. 探测与控制学报, 2014, 36(4): 30-35. [14]ELADM.OptimizedProjectionsforCompressedSensing[J].SignalProcessing,IEEETransactionson, 2007, 55(12): 5695-5702. [15]DUARTE-CARVAJALINOJM,SAPIROG.LearningtoSenseSparseSignals:SimultaneousSensingMatrixandSparsifyingDictionaryOptimization[J].ImageProcessing,IEEETransactionson, 2009, 18(7): 1395-1408. Performance Criteria of Measurement Matrices in Signal Reconstruction CHENG Tao1,2,3 (1. Key Laboratory of Optoelectronic Devices and Systems of Ministry of Education and Guangdong Province, College of Optoelectronic Engineering, Shenzhen University, Shenzhen 518060, China; 2. Automotive & Transportation Engineering Institute,Guangxi University of Science and Technology, Liuzhou, 545006, China;3. Shenzhen Key Laboratory of Micro-Nano Measuring and Imaging in Biomedical Optics of Shenzhen, College of Optoelectronic Engineering, Shenzhen University, Shenzhen, 518060, China) Aiming at the confusing problem of measurement matrix performance criteria, the performance criteria of the measurement matrix based on different types of reconstruction algorithms were proposed. The operatebility of this criterion was better than the traditional method. The strict contrast experiments were implemented on matrices with different columns correlation by this method when other properties of matrices were almost identical. Experimental results showed that column incoherence of a measurement matrix could be taken as the performance criteria of the measurement matrix for OMP (orthogonal matching pursuit). However, the performance of the measurement matrix did not be affected when the correlation was enough between the columns. The performance of the measurement matrices with the same solution space had no relation with the column correlation for BP(Basis Pursuit). Measurement matrix correlation was not the main criteria to determine the performance of the measurement matrix. Theoretical upper limit of the matrix was reconstruction ability of Hadamard matrix in same scale. compressive sensing; measurement matrix; signal correlation; solution space 2016-02-15 国家自然科学基金资助项目(41461082);中国博士后科学基金资助项目(2016M592525);广西自然科学基金资助项目(2014GXNSFAA118285);广西高校科学技术研究项目资助(YB2014212);广西科技大学博士基金资助项目(校科博13Z12) 程涛(1976—),男,广西柳州人,博士,副教授,研究方向:压缩感知和遥感。E-mail:ctnp@163.com。 TP391 A 1008-1194(2016)04-0072-05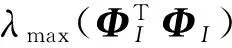
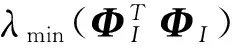
2 测量矩阵性能的判据
3 实验结果和分析


4 结论

