基于误差合成的射程修正系统精度评估

薛　冰，霍鹏飞，杨小会

(西安机电信息技术研究所，陕西 西安　710065)



基于误差合成的射程修正系统精度评估

薛冰，霍鹏飞，杨小会

(西安机电信息技术研究所，陕西 西安710065)

针对修正系统误差源对精度影响权重的问题，提出基于误差合成的一维弹道修正系统精度评估方法。该方法通过计算修正系统误差源的敏感因子，再结合各误差源散布，计算各误差源对系统精度的影响权值。仿真表明，影响修正系统精度的主要因素为卫星定位速度测量误差、阻力器气动误差及弹道纵风误差；计算了在最大射程时修正系统的纵向综合概率误差。

一维弹道修正；系统精度；评估；误差合成

0　引言

一维弹道修正系统是一种以修正引信为主体，与目标射距相关联的纵向准精确打击武器系统，能同时降低原有无控弹的射击准确度和密集度误差，其误差为相对目标的纵向精度[1]。但是目前一维弹道修正系统的指标均采用纵向密集度，无法全面有效评判火炮系统的射击精度。

目前，关于修正系统精度的评估主要采用靶场验证方法和蒙特卡罗模拟打靶方法[2]，靶场验证需要大量试验，成本高且不易实现；蒙特卡罗方法通过大样本量模拟可以仿真实际精度，但计算时间长。且这两种方法均无法直观、定量地看出影响系统精度的各误差因素的权值。为解决此问题，本文提出基于误差合成的射程修正系统精度评估方法。

1　控制策略与计算原理

1.1一维弹道修正系统控制策略

一维弹道修正系统采用瞄远打近、增阻减速方案，基于目标射距确定修正的阻力器打开时间，即引信直接与目标相关联，同时降低原有无控弹的射击准确度和密集度误差，其误差为相对目标的纵向精度。

如图1所示，一维弹道修正引信在获得目标射击诸元后，将火炮瞄向比目标更远的一个位置进行射击；弹丸发射后，采用卫星定位获取弹丸飞行参数，根据实测弹丸位置、速度预测无控弹射距；将预测的无控弹射距与目标射距相比，计算射距修正量，并据此射距修正量计算阻力器打开时间，控制阻力器适时展开，使弹道阻力增大，调整弹丸射距，使其飞向目标位置。

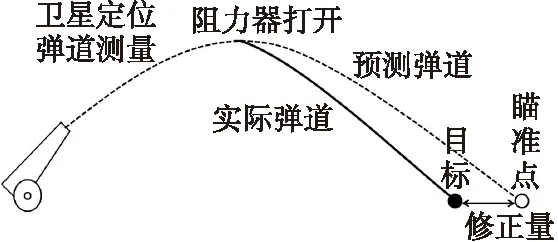
图1　一维弹道修正工作原理示意图Fig.1　Basic theory of 1-D correction fuse

1.2目标关联

一维弹道修正系统是一种与目标射距相关联的武器系统，其误差为相对目标的纵向精度，采用以目标为中心的综合概率误差来表示。

(1)

1.3误差合成法

设随即变量X,Y,Z,…的概率密度函数及联合概率密度函数已知，求N=f(X,Y,Z,…)的概率密度或分布函数。采用“方和根合成”的误差合成方法，即把分误差取平方相加后再开方的方法[4]，计算N的概率密度。

(2)

1.4六自由度刚体弹道模型

在弹箭刚体运动方程组的基础上，引入有风情况下的启动力和力矩分量，将作用在弹体上的力和力矩进行分解计算，即引入弹箭运动的6D刚体弹道方程[5]。

将地球自转角速度分量转到速度坐标系中，科氏惯性力分解到速度坐标系，略去动不平衡与横向角速度等乘积项，得到弹箭6自由度缸体运动方程组如下：

(3)

式(3)中，r，v,θ,ω分别为弹体的位移、速度、绕弹体系X轴转动角度、角速度，Fiw为弹丸所受的气动力，g为重力加速度，ak为科氏加速度，M为翻转力矩和马格努斯力矩的合力矩，M阻尼为阻尼力矩，J为弹丸在准弹体系下的动量矩，以上各量除质量m外均为矢量。

2　基于误差合成法的系统精度评估

采用单一变量法计算不同误差源的敏感因子，再结合其误差散布，对各误差源的概率误差进行综合，合成一维修正系统精度误差。计算时，先通过无控弹相关信息或文献值确定误差源散布；而后，通过误差合成法合成系统精度，计算各误差影响权值。

本文涉及敏感因子，文献[6]中也涉及敏感因子，采用加速度、速度、高度对速度测量误差的敏感因子，但所用的变量、方法均有所不同。

2.1误差源

影响弹丸射程精度的误差主要有射击误差、弹丸自身误差、弹道环境误差及一维弹道控制系统引起的误差。

1)射击误差

射击误差主要包括初速、射角及初始扰动等误差，影响无控弹丸的落点精度。由于一维弹道修正引信采用卫星定位实时测量弹丸弹道参数，因此该类误差最终归结于为弹道测量误差中，包括水平位置(X)，垂直位置(Y)，水平速度(Vx)，垂直速度(Vy)。

2)弹丸自身误差

弹丸自身误差主要包括制式弹丸质量误差(m)、弹形系数误差(i0)等。制式弹丸的质量和气动误差采用弹厂的设计指标。

3)弹道环境误差

弹道环境误差主要为气象误差，包括气压(p)、纵风(Wx)、气温(T)等。气象误差采用文献值。

4)控制系统引起的误差

控制系统引起的误差主要包括弹道测量误差、阻力器引起的气动误差等，弹道测量误差包括弹丸的位置、速度测量误差。控制系统引起的误差采用外场实测数据。

2.2误差因素敏感因子计算

采用六自由度刚体弹道模型，采用单误差因素变化法计算各误差因素对射程影响的敏感因子，即引入单一误差，使其在其误差范围内线性增加，计算弹丸射程，与没有引入误差的弹丸射程进行对比，计算引入误差后的射程变化量，对射程变化量进行多项式拟合，计算该误差源相对射距的敏感因子。

2.3系统精度评估

(2) 有关微网电能质量的关注点 微网内存在逆变器型微电源和旋转电机型微电源(微型燃气轮机)以及大量的非线性负载,可能会造成谐波污染、电压波动、电压(频率)闪变、环流等问题,所以微网的电能质量问题依然是未来微网的研究热点之一。

首先计算各误差源对射程准确度的影响，而后计算其对系统精度的影响权值，最后合成系统精度。

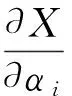
(4)

由公式(4)可以看出各误差因素对射程准确度的影响权值。

根据各因素对射程准确度误差的影响EXαi可以计算出系统的射程准确度EX：

(5)

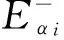
(6)

由公式(6)可以看出各误差因素对射程密集度的影响权值。

(7)

根据射程准确度误差和密集度误差，采用公式(1)即可计算出系统在此射距下的综合概率误差。

3　仿真验证

以155mm榴弹为仿真平台，计算最大射程38km条件下一维弹道修正系统作用后的综合概率误差。

3.1误差合成

根据卫星定位精度确定X、Y、Vx、Vy的误差取值，根据文献值确定气象误差(p、Wx、T)取值，155mm弹自身误差(质量误差(m)、弹形系数误差(i0))采用文献[3]提供数据，阻力片带来的气动误差(id)采用实验室吹风数据。结合以上误差源取值，以6D弹道模型，计算一维弹道修正系统各误差因素对射程的敏感因子，见表1。

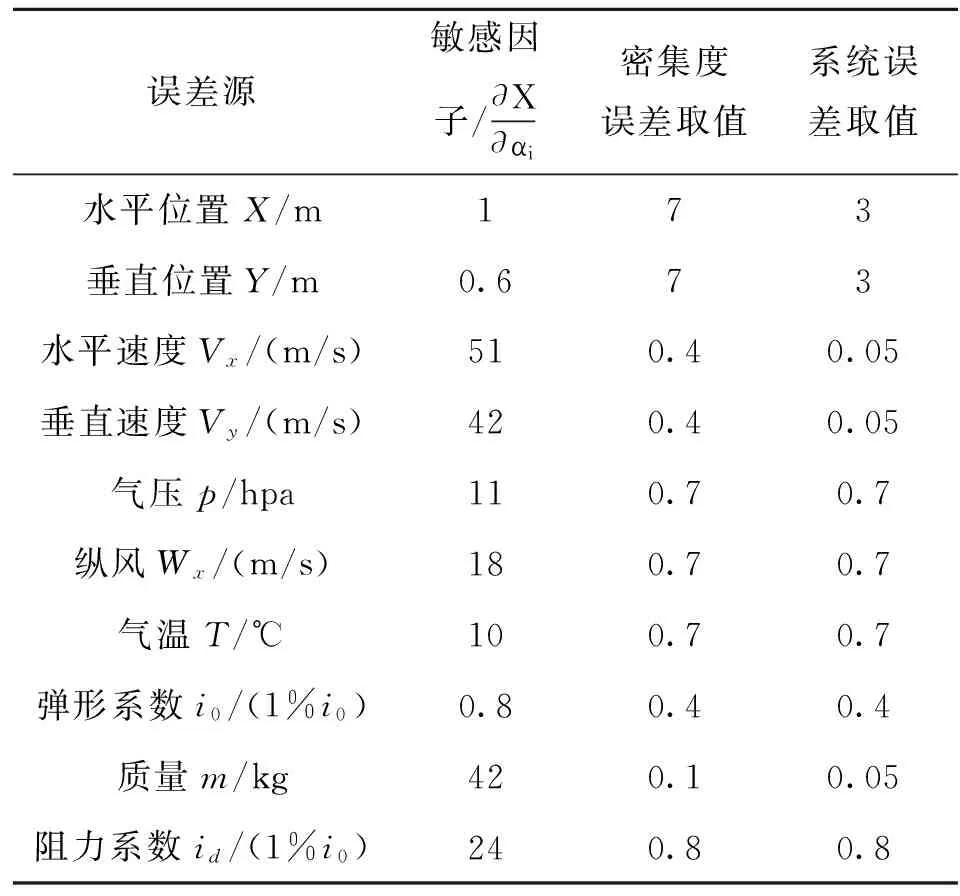
表1　155 mm榴弹射击误差源敏感因子及取值

根据表1，计算155 mm榴弹最大射程一维弹道修正系统作用后的密集度误差和准确度误差，结果见表2。

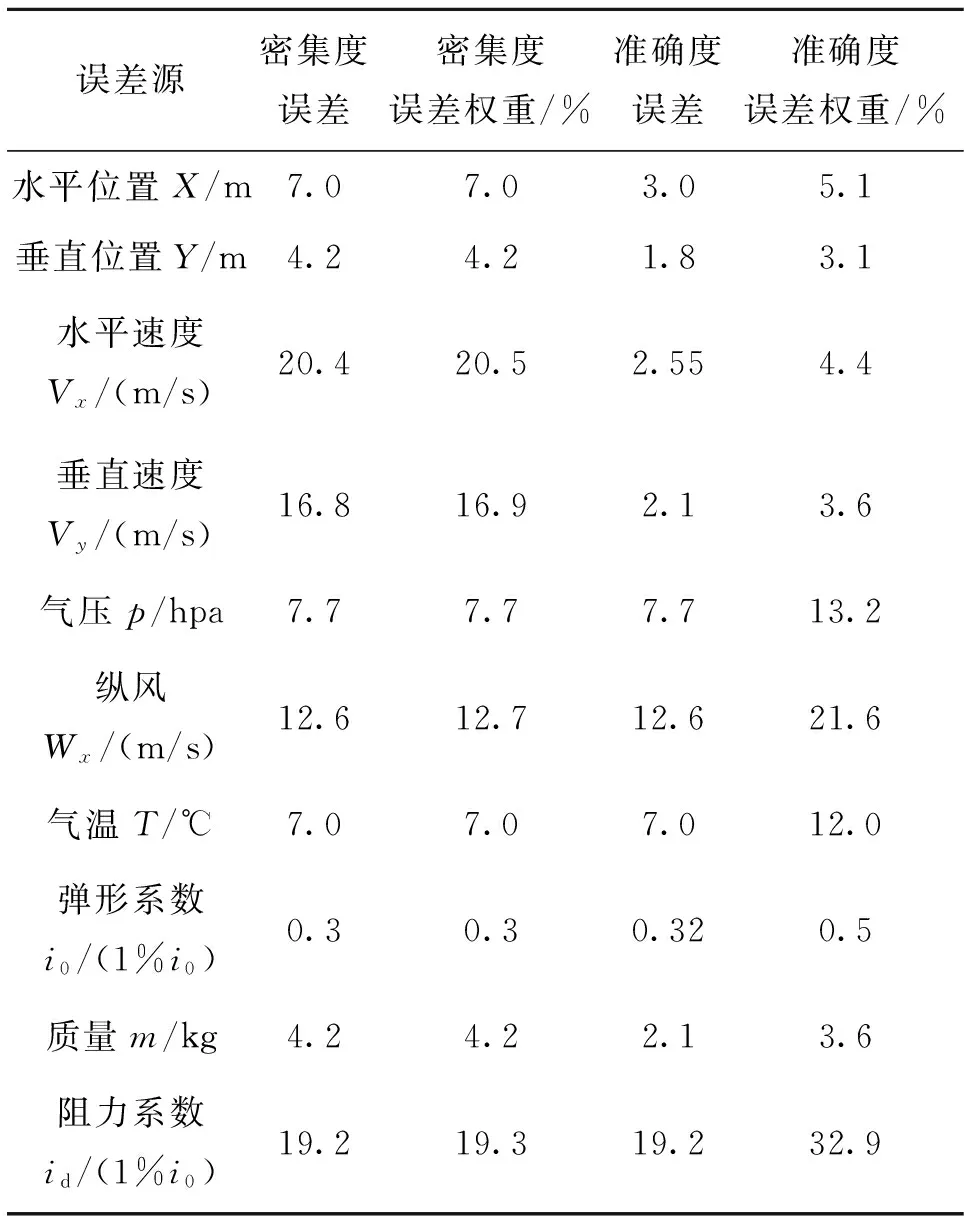
表2　155 mm榴弹最大射距一维弹道修

由表2可得，在最大射程时，修正系统纵向综合概率误差为46 m，与欧洲修正引信(ECF)纵向综合概率误差50 m的指标相当。

根据表2，绘制各误差源分别对纵向密集度及纵向准确度的误差贡献直方图，见图2、图3。

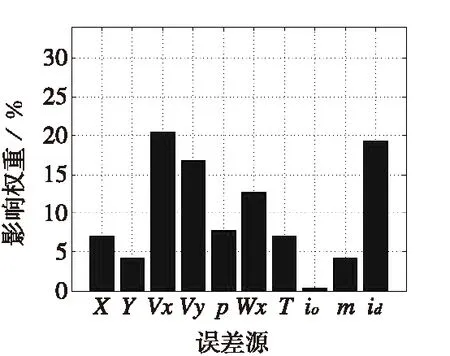
图2　各误差对密集度的贡献直方图Fig.2　Contribution to intensity error

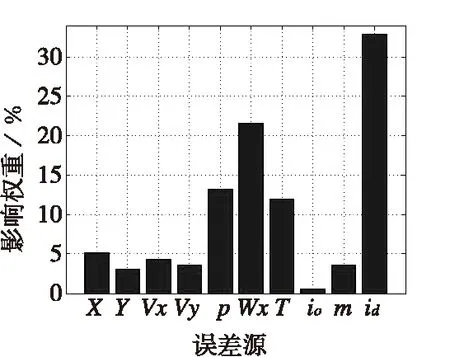
图3　各误差对准确度的贡献直方图Fig.3　Contribution to accuracy error

由图2、图3可见，影响修正系统准确度的主要因素为阻力器气动误差(id)和气象误差(p、Wx、T)，影响修正系统密集度的主要因素为卫星定位速度测量误差(Vx、Vy)、阻力器气动误差(id)和弹道纵风误差(Wx)。其中，Vx、Vy对系统密集度影响较大，而对准确度影响较小。而气动(id)和纵风(Wx)对准确度及密集度影响都很大，尤其是阻力片引起的气动引起误差占准确度误差权重超过30%。因此，准确测量纵风和计算阻力器风阻系数对修正系统的精度尤为重要。而在器件设计中，提高卫星测速的精度，减小测速误差，对修正系统精度提升应有较大贡献。

3.2蒙特卡罗模拟验证

采用蒙特卡罗模拟打靶[7]的方法，进行仿真验证，步骤如下：

1)以6D弹道模型为基础，引入修正引信射距预测、控制程序，在Matlab下建模。

2)确定弹丸发射、飞行中各种随机误差，引入Matlab模型。

3)Matlab下编制M-file作为蒙特卡罗方法主程序，一方面根据各误差源分布规律产生随机变量，另一方面通过主程序循环调用获得随即弹道数据仿真，即模拟打靶。

4)对仿真结果进行统计处理。

由于在实际设计中，气象和风阻系数不可控因素较多，而提高卫星测量精度是较为可行的方法，因此，在仿真中，分别以原卫星测速精度(X、Y向速度误差取值均为0.4 m/s)和提高后的卫星测速精度(X、Y向速度误差取值均为0.2 m/s)进行仿真，模拟打靶1 000次的统计结果表明，原综合概率误差为45 m，与误差合成法计算结果(46 m)相吻合。提高卫星精度后，概率误差统计值为36 m,精度提高达20%，此结果与误差合成法的分析结果基本吻合。

4　结论

本文提出了基于误差合成法的一维弹道修正系统精度评估方法。该方法通过计算修正系统误差源的敏感因子，再结合各误差源散布，计算各误差源对系统精度的影响权值。仿真表明，影响修正系统精度的主要因素为卫星定位速度测量误差、阻力器气动误差和弹道纵风误差。在最大射程时，修正系统纵向综合概率误差为46 m，与欧洲修正引信(ECF)纵向综合概率误差50 m的指标相当。改变误差取值后，用蒙特卡罗法模拟打靶的方法进行模拟，统计精度与原精度相比，结合所对应权重，结果表明数据吻合，证实了方法的准确性。

[1]张民权,刘东方,王冬梅.等.弹道修正弹发展综述[J].兵工学报，2010(s2):127-130.

[2]侯宏录,闫帅,刘创, 等.一种弹道射程偏差预测方法的精度分析[J].理论与方法,2008,27(8):1-5.

[3]郭锡福.远程火炮武器系统射击精度分析[M].北京:国防工业出版社,2004：42-49,94-117.

[4]费业泰.误差理论与数据处理[M].北京:机械工业出版社,2004：55.

[5]韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008:127-143.

[6]李小平,霍鹏飞,杨小会.基于敏感因子的GPS速度测量误差补偿算法[J].探测与控制学报,2015(4):31-34.

[7]王华,徐军,张芸香.基于Matlab的弹道蒙特卡洛仿真研究[J].弹箭与制导学报,2005,25(1):181-183.

Error Combination Based Range Correction Accuracy Evaluation

XUE Bing, HUO Pengfei, YANG Xiaohui

(Xi’an Institute of Electromechanical Information Technology, Xi’an 710065, China)

As to the problem that the firing accuracy influenced by error sources differs from each other, an error combination method was proposed to evaluate the accuracy of the 1-D course corrected fuze system. In this method, the weight of every error source was calculated through a combination of sensitive factors and their distribution of values .The result of mathematical simulation showed that the main factors that make more contribution to firing accuracy error were velocity measurement error, drag coefficient error of the drag-mechanism and range wind error; The CEP at the maximum range was also calculated.

1-D correction; firing accuracy; evaluate; error combination

2016-02-26

薛冰(1990—)，男，陕西咸阳人，硕士，研究方向：弹道修正引信。E-mail:aliboke@126.com。

TJ430

A

1008-1194(2016)04-0058-04