基于二维波束控制引信的起爆控制方法

吉　阳，简金蕾，任宏滨，徐　跃

(空军工程大学防空反导学院，陕西 西安　710051)



基于二维波束控制引信的起爆控制方法

吉阳，简金蕾，任宏滨，徐跃

(空军工程大学防空反导学院，陕西 西安710051)

针对传统的波束倾角固定引信无法满足新一代防空导弹引战配合需求的问题，提出了基于二维波束控制引信的起爆控制方法。该方法通过将平面相控阵技术引入引信天线，实现了波束的二维控制。在此基础之上建立了引信最佳起爆角和起爆方位模型并设计了基于波束分档前提下的起爆控制算法，保证了二维波控引信与定向战斗部的有效配合。在H平面内，根据起爆方位角来选择战斗部的起爆点；在E平面内利用波束倾角分档控制和延时调整炸点的方法，把修正后所对应的起爆角与动态破片飞散角差值作为起爆控制量，实现智能化引战配合。仿真分析表明该方法可实现战斗部适时起爆并将破片飞散方向对准目标，显著提高了引战配合效率。

二维波控引信；波束分档离散控制；最佳起爆角；起爆方位；智能化引战配合

0　引言

现代战争随着防空导弹作战空域及目标速度范围的不断扩大，防空范围从点面防空至区域防御，这就要求导弹既能拦截普通飞机等低速目标，又能对付战术弹道导弹(TBM)等高速目标，致使导弹与目标的交会条件变化范围增宽，引战配合难度加大[1]。传统的波束倾角固定引信无法满足新一代防空导弹引战配合的需求,因而将平面相控阵技术引入引信天线中，利用其扫描速度快、波束控制灵活且具有较强的抗干扰能力等特点实现对防空反导导弹引信天线的二维波束控制，保证引信对多种目标的自适应跟踪，便于与定向战斗部配合[2]，获得最佳杀伤效果。美、俄、英、德等国已在厘米波段和毫米波段的雷达导引头中引入了相控阵技术，但该技术在引信上的应用尚未见报道。以往的研究中，只有针对引信波束一维控制及其起爆控制算法[3]的探讨，对二维波束控制以及如何实现对定向战斗部的最佳起爆控制缺少分析和研究。本文针对此问题，提出了基于二维波束控制引信的起爆控制方法。

1　模型的建立

二维波控引信充分利用波束快速无惯性灵活扫描的特点，自适应地跟踪目标，适时启动定向战斗部杀伤目标，二维波控引信起爆系统如图1所示。

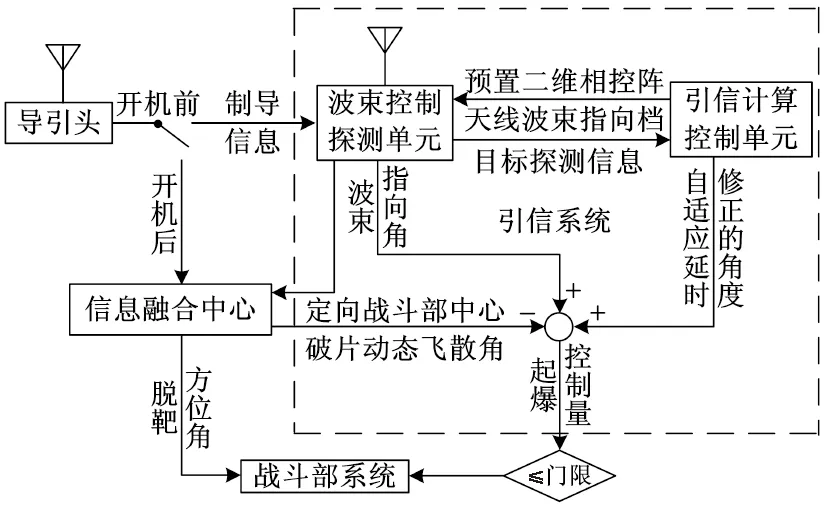
图1　二维波控引信起爆系统框图Fig.1　The block diagram of two-dimensional beam controlling fuze detonating system

根据导引头获得的交会条件预置二维相控阵引信天线波束指向挡并且根据起爆方位角选择定向战斗部的起爆点。在天线波束分档的前提下，引信获得最佳起爆角ψ后，控制波束指向距离最近的波束档，并且保证波束和弹轴之间的夹角要小于ψ。这样虽然可以在一定程度上保证炸点不滞后，但是在某些情况下，比如破片宽度比较小，ψ的误差比较大等等，就有可能使炸点超前。所以，在对精度要求比较高的情况下，为进一步提高引战配合效率，需要再进一步通过自适应延时来调整炸点位置。从起爆角的角度来看，延时等于引信天线波束分档后对起爆角进行修正，将修正后所对应的最佳起爆角 (由延时修正的角度+波束指向角)与定向战斗部中心破片的动态飞散角的差作为战斗部起爆控制量，当差值为0或小到一定范围，引信起爆战斗部杀伤目标。

1.1弹目交会运动模型

在导弹和目标交会段，由于距离近、时间短、速度大，导弹和目标已来不及做机动飞行，相对速度矢量的方向基本不变，因此可建立近场弹目交会模型[4]：假设在弹体坐标系中，OZ轴为导弹速度方向并且与导弹纵轴重合。VR为弹目相对速度，VA为战斗部静态破片飞散速度，破片静态飞散中心与弹轴垂直。A点为相对速度-VR方向与弹体坐标系XOY平面的交点，OP为弹体坐标系中的脱靶量。中心破片动态速度矢量VB是弹目相对速度矢量VR与战斗部静态破片速度矢量VA之和。则在弹体坐标系下的近场交会示意如图2所示。

图2　近场弹目交会几何图Fig.2　Missile-target encountering trajectory phase

图2中，β为弹轴与目标相对运动速度的夹角，ε为目标相对运动速度与弹目连线的夹角。

1.2最佳起爆角

参考图2，在弹体坐标系中，最佳起爆角ψ可定义为中心动态破片密度方向VB与导弹弹轴方向的夹角即

(1)

式(1)中，VB=VA+VR。则根据弹目交会几何关系可得最佳起爆角为：

(2)

式(2)中，φT～φA在0°～360°范围内变化，当战斗部中心破片静态速度和弹目相对速度一定时，ψ分别在φT-φA=0o和φT-φA=180o时取得最大值和最小值，相对应的最佳起爆角散布图如图3所示。

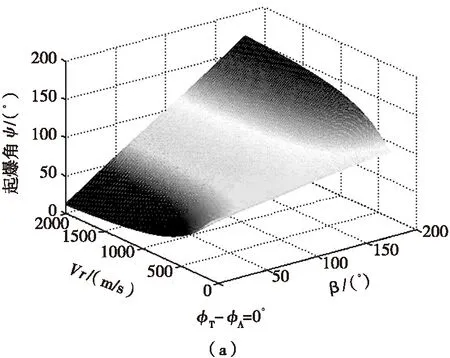
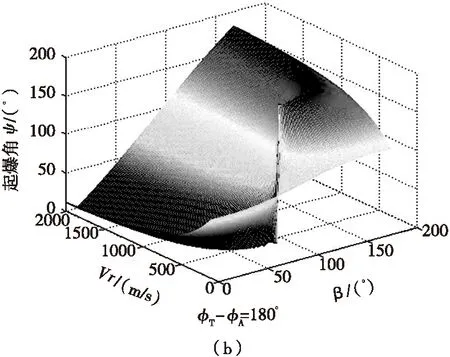
图3　最佳起爆角散布图

1.3最佳起爆方位

A点是相对速度-VR方向与弹体坐标系XOY平面的交点，OA与OX的夹角定义为起爆方位角，用φA表示。由几何关系可得方位角为：

(3)

2　起爆控制优化设计

2.1二维波束控制

平面相控阵天线可以同时实现天线波束在仰角和方位两个方向上的相控扫描。因而若将相控阵技术引入导弹引信中，则能够实现引信天线的二维控制。设天线单元按等间距矩形格阵排列，如图4所示。图中阵列在XOY平面上共有M×N个天线单元，单元间距分别为d1和d2。

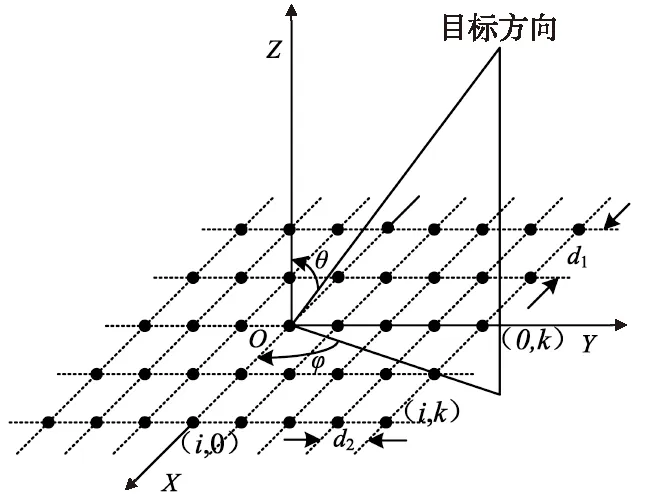
图4　平面矩形相控阵天线单元排列示意图Fig.4　Pareto chart of rectangle phased-array antenna on plane

若假设目标所在方向以方向余弦表示为(sinθcosφ,sinθsinφ,cosθ)，则图4所示平面相控阵天线的方向图F(θ,φ)可表示为：

(4)

式(4)中，αik为第(i,k)单元的幅度加权系数，ΔφBα和ΔφBβ分别为天线阵内移相器在X和Y方向上相邻天线单元之间的相位差。

由上可以看出，当(2π/λ)d1sinθcosφ=ΔφBα且(2π/λ)d2sinθsinφ=ΔφBβ时，可得到天线方向图最大值。因此改变阵内相邻单元之间的相位差ΔφBα和ΔφBβ就能改变天线波束指向，形成波束扫描。

对于不同的馈电方式，波束指向的调整方式也不同，如果采用连续式移相器，则天线波束可实现连续扫描；如果采用数字式移相器，则天线波束可实现离散扫描。

2.1.1波束宽度

定义半功率波束宽度为主瓣最大值两边场强等于最大场强的0.707倍，也就等于最大功率一半的两个平面的夹角，又称3 dB波束宽度[5]。平面相控阵天线的方向图是立体图形，它的波束宽度一般在两个相互正交的平面上考察，均匀正方形孔径相控阵天线在E面(θ方向)的波束扫描宽度与扫描角和阵列孔径尺寸大小有关，而在H面(φ方向)扫描波束在XOY平面上的投影只作平移所以波束宽度保持不变。

当平面相控阵天线波束扫描到(θB,φB)方向时，E面内波束宽度σ可由下式求得。

(5)

对于大扫描角，波束宽度σ近似为：

σ=σ0/cosθB

(6)

式(6)中，σ0为波束指向天线阵面法线方向时的宽度，即等于在H面内的波束宽度。

2.1.2天线增益

对于等幅口径分布，天线增益的理论值为：

G=(4π/λ2)Ae

(7)

式(7)中，Ae为天线有效口径面积，对于M×N个单元间距为d1和d2的平面阵，Ae最大为天线口径面积A，天线面积为：

A=MNd1d2

(8)

当波束扫描到(θB,φB)方向时，天线增益为：

G=(4π/λ2)AcosθB

(9)

2.1.3阵元间距

对于矩形栅格，应在不出现栅瓣的条件下，选择尽可能大的阵元间距，使阵元数减少。如果工作频段和最大扫描角θm确定，则相控阵天线阵元的理论最大间距d1,d2为：

(10)

2.1.4参数选择

二维波控引信天线的技术参数选择如下：工作频率f=15 GHz；扫描范围为E面(θ方向)为±65°、H面(φ方向)为360°；天线增益G大于20 dB；旁瓣电平小于-30 dB。取均匀正方形面阵尺寸大小为20 cm×20 cm，阵元数为35×35，则d/λ=0.285 7。通过计算仿真得到的平面相控阵天线波束宽度与天线增益随波束扫描角变化关系曲线如图5所示。

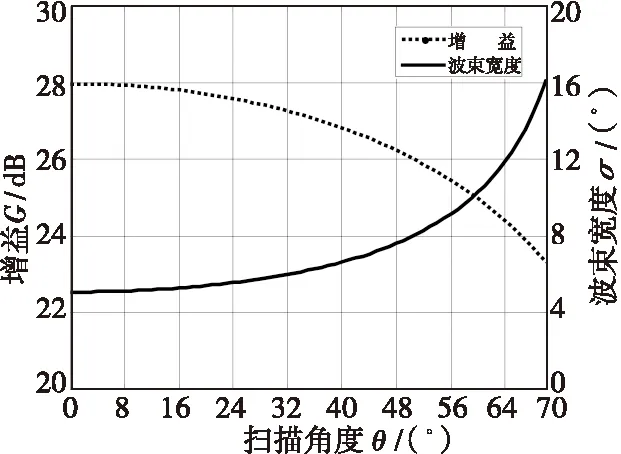
图5　波束扫描角与增益及波束宽度的关系曲线Fig. 5　Relations of beam-scanning angle, antenna gain and wave disc width

由图中可以看出，波束扫描时，随着波束指向角θ的增大，E面内波束宽度σ要展宽，范围大概在4°～16°，而天线的增益随着指向角的增大有所下降，但均大于20 dB。

根据所设计的二维波控引信天线波束扫描范围，可将波束指向：E面0°～65°(与弹纵轴之间夹角)和H面0°～360°进行等间隔离散分档。

在E平面内波束指向共分为9档，且每个波束指向之间的夹角相等，相控阵阵内相位差由数字移相器提供。假设第一个波束指向为0°，最后一个波束指向为64°，中间8个波束之间的夹角为8°，波束档位依次编号θi，i=0,1,2，…，8。E平面内波束不同指向档位中的增益和波束宽度变化关系如表1所示。

在H平面内依据起爆方位范围将区域分为8档，从X轴正方向开始，每隔45°为一档，同时将二维波控引信与定向战斗部[6-7]相结合，定向战斗部采用多点起爆方式，根据起爆方位角的大小选择相对应的起爆档位，使破片飞散方向对准目标。沿战斗部径向均匀设置的8个起爆点如图6所示。H平面内的起爆方位角和所选择的起爆点的对应关系如表2所示。

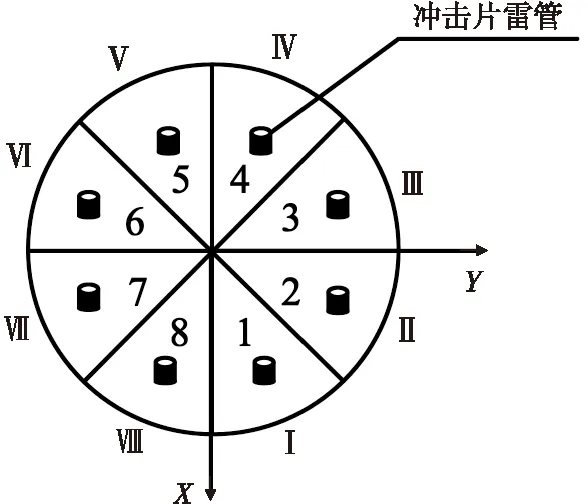
图6　多点起爆系统分布示意图Fig.6　The diagram of multi-point detonating system

2.2引信自适应起爆延迟时间的调整

为了弥补引信天线在E平面内的波束分档可能导致的超前起爆，可以通过增加引信自适应延迟时间来对起爆角进行修正，根据修正后所对应的起爆角与动态破片飞散角差值来控制起爆。引信起爆延迟时间定义为从探测到目标到起爆战斗部所经历的时间间隔。

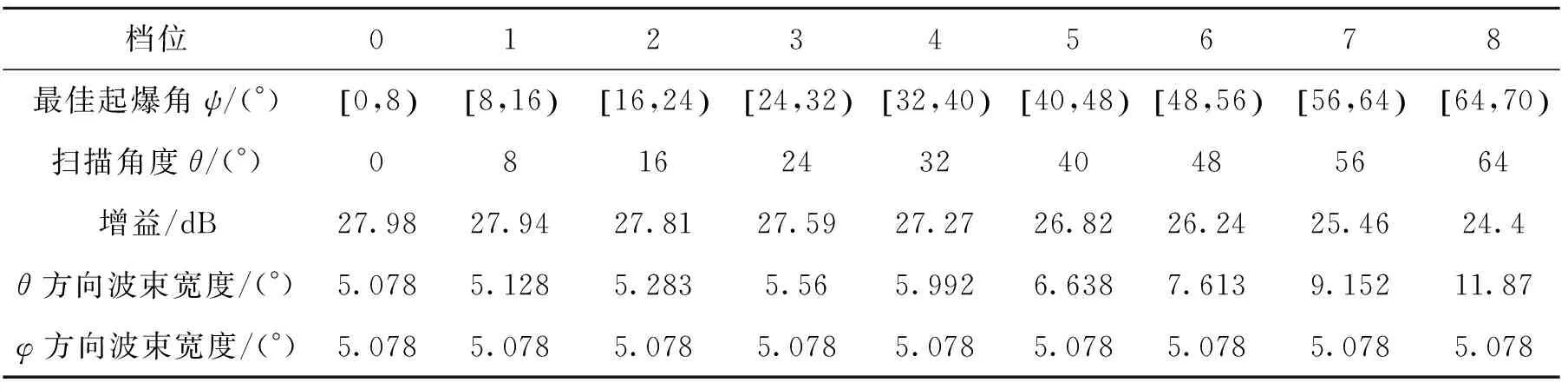
表1　E平面内波束不同指向档位中的增益和波束宽度变化关系

表2　H平面内的起爆方位和所选起爆点的对应关系

引信起爆延迟时间的设计，包括固有延时τs和可调延时tD的设计，前者主要用于提高引信抗外来和自身的瞬时尖头脉冲干扰的能力而后者则是为了满足引战配合的需要，通常利用制导系统获得的多普勒频率、相对速度、脱靶量、脱靶方位等信息进行自适应调整。

2.2.1引信固有延时的设计

假设在弹目共面交会时，弹速与弹轴重合，导弹和目标均做匀速直线运动，空间交会如图7所示。设二维波控引信天线的波束指向角为θ,天线在E平面内的主波束宽度为σ，目标轴线与相对速度的夹角为δ。

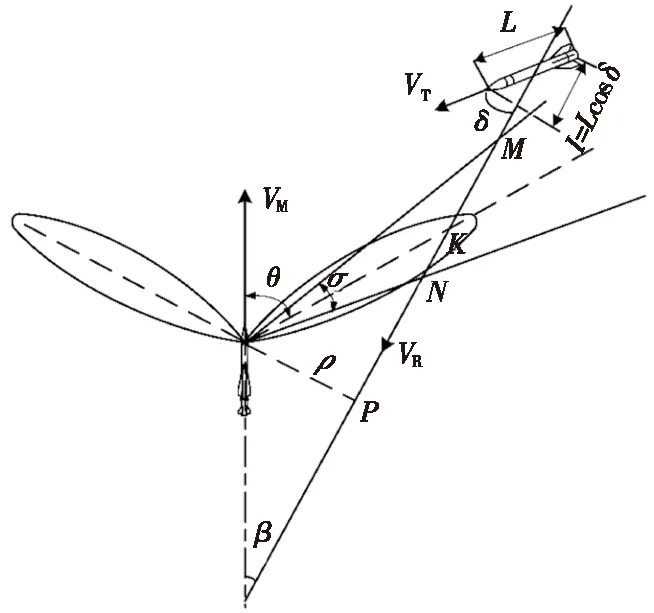
图7　目标相对运动轨迹与天线波束的交会几何图Fig.7　 The geometric figure of antenna beam and target motion

假设目标穿越天线波束时间tx，目标线长度为L，根据交会几何图，可得：

(11)

式(11)中，l=Lcosδ，α=θ-β。

(12)

固有延迟时间τs的设计应满足：

(13)

式(13)中，ΔfZ表示干扰噪声带宽。一般情况下，目标穿越天线波束时间至少是系统固有延迟时间的5倍，即

τs≤tx/5

(14)

2.2.2引信可调延时的设计

引信在弹目交会过程中，根据制导系统以及自身所获取的相关信息，实时调整其延迟时间tD的设置，实现最佳起爆，以进一步提高引战配合效率。

根据图2近场弹目交会几何关系，引信可调延迟时间tD可表示为：

(15)

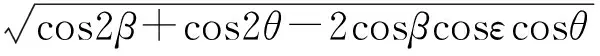
由于VR=fdλ/2cosε，所以引信可调延迟时间可算得：

(16)

式(16)中，a=cosβ,b=cosθ,c=fdλ/2，λ为引信工作波长；fd为对应波束倾角θ时的多普勒频率。

3　仿真分析

引信起爆延迟时间tQ为固有延时τs与可调延时tD之和，即tQ=τs+tD，那么

(17)

假设目标长度L=15 m，载波波长λ=0.02 m，引信波束宽度σ=6°，相对速度大小为VR=1 000 m/s，战斗部的破片速度VA=2 100 m/s，目标的初始位置是(-600 m,300 m,500 m)，距离测量误差在 (-20 m,20 m)之间均匀分布，角度测量误差在(-20 mrad,20 mrad)之间均匀分布，采样时间为T=5 ms。图8和图9分别为用卡尔曼滤波器输出参数估计的起爆方位和最佳起爆角随剩余飞行时间的变化曲线。

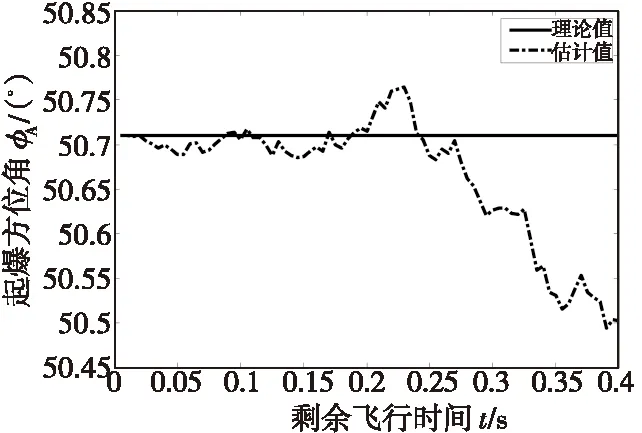
图8　起爆方位角的估算Fig.8　Estimate of detonating azimuth

由图可见，随着剩余飞行时间的减少，估算的起爆方位、 最佳起爆角都越来越接近真实值， 误差极

小。那么，越接近目标滤波所得到的数据利用的可信度就越高。在这种精度的保证下，考虑用波束分档控制和延迟调整来控制炸点位置，可以实现很高的命中概率。根据表1的分类，起爆控制参量变化结果如图10所示。利用延迟时间对起爆角的修正实现对炸点的控制，炸点误差偏差如图11所示。从图中可以看出，根据破片动态飞散角的大小调整波束指向档位并利用延迟完成对起爆角的修正，从而能保证导弹在最佳炸点附近毁伤目标。

图9　最佳起爆角的估算Fig.9　Estimate of optimum detonating angle

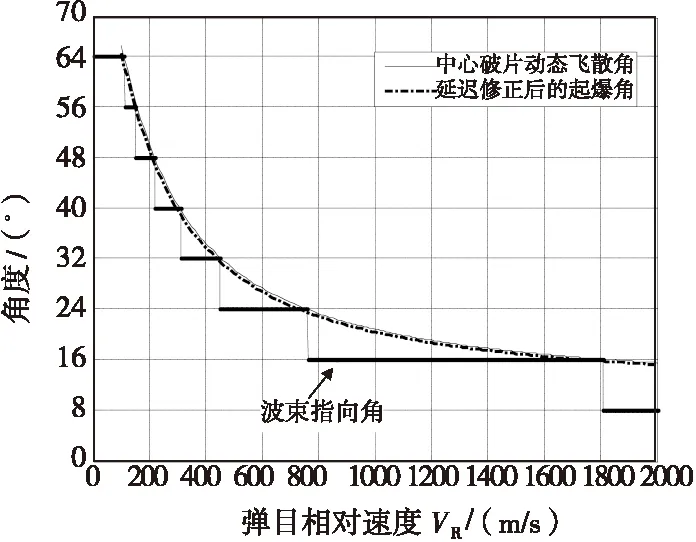
图10　起爆控制参量变化图Fig.10　Controlled variable of fuze action

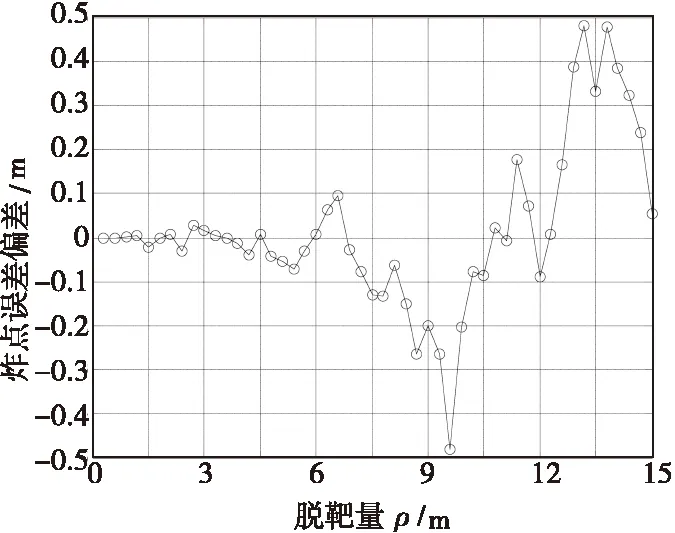
图11　炸点误差偏差Fig.11　The error of detonating point

4　结论

本文提出了基于二维波束控制引信的起爆控制方法。该方法与传统的波束倾角固定引信起爆模型相比，通过将平面相控阵技术引入引信天线，实现了波束的二维控制同时设计了基于波束分档前提下的起爆控制算法，保证了二维波控引信与定向战斗部的有效配合。仿真分析表明该方法可实现战斗部适时起爆并将破片飞散方向对准目标，显著提高了引战配合效率。本文只研究了二维波控引信的起爆控制算法，拟对模型的工程化、制导信息的综合利用等方面的工作做进一步的研究。

[1]蒋静群,简金蕾,张晓.制导信息协同下的最佳起爆控制分析与研究[J].现代防御技术,2009,37 (3) : 19-25.

[2]李静,简金蕾,任宏滨.二维波束控制引信与定向战斗部配合[J].现代防御技术,2010,38 (6): 56-60.

[3]刘剑锋,庄志洪,陈潜.基于一维相控阵引信的起爆控制算法研究[J].宇航学报,2005,26 (4): 466-470.

[4]MarkEngel，eithLewis，HowieWendt.GIFGuidanceIntegatedFuze[C]//NDIA47thFuzeConferenee.US:NDIA,2003.

[5]王新稳,李延平,李萍.微波技术与天线[M].北京:电子工业出版社,2011.

[6]韩克华,任西,张玉若，等. 定向战斗部直列式多点起爆系统设计[J]. 弹箭与制导学报,2013,33(6):78-81.

[7]郭泽荣,李洛,李元.六光束脉冲激光探测定向战斗部最佳起爆延时研究[J]. 北京理工大学学报,2014, 34(6):588-591.

Initiating Control of Two-Dimension Beam Controlled Fuze

JI Yang，JIAN Jinlei，REN Hongbin，XU Yue

(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)

The traditional fuze beam angle is fixed, which can't meet the demand of air defense missile. Aiming at this problem, a new method of initiating control based on two-dimension beam controlled fuze was proposed in this paper. This method introduced the fuze antenna based on planar phased array technology and two-dimension beam control was realized. On this basis, a new model of the optimum detonating angle and initiating direction was established and the initiating control algorithm based on beam step was designed, which guaranteed the effective cooperation of two-dimension beam controlled fuze and aimed warhead. In the H-plane, an appropriate initiation point of the aimed warhead according to the discrete azimuth can be chosen. In the E-plane, according to the discrete beam angle and adaptive detonating delay algorithm, it can realize intelligent coordination that taking the difference between the detonating angle which has been corrected and dispersion directional angle of center fragment as controlled variable of fuze action. Simulation indicates that this method can control adaptively the detonation of warhead and make the fragment aim at the target. The coordinated efficiency of fuze and warhead can be improved very well.

two-dimension beam controlled fuze; discrete control of beam directions; optimum detonating angle; initiating direction; intelligent coordination of fuze and warhead

2015-12-03

吉阳(1992—)，男，江苏南通人，硕士研究生，研究方项：引制一体化二维波束控制及引战配合。E-mail:644942351@qq.com。

TJ430

A

1008-1194(2016)04-0052-06