Self-consistent Sources and Conservation Laws for Super-Geng Equation Hierarchy

WEI Han-yu，CUI Zhong-yuan，XIA Tie-cheng

（1.College of Mathematics and Statistics，Zhoukou Normal University，Zhoukou 466001，China；2.College of Computer Science and Technology，Zhoukou Normal University，Zhoukou 466001，China；3.Department of Mathematics，Shanghai University，Shanghai 200444，China）



Self-consistent Sources and Conservation Laws for Super-Geng Equation Hierarchy

WEI Han-yu1，CUI Zhong-yuan2，XIA Tie-cheng3

（1.College of Mathematics and Statistics，Zhoukou Normal University，Zhoukou 466001，China；2.College of Computer Science and Technology，Zhoukou Normal University，Zhoukou 466001，China；3.Department of Mathematics，Shanghai University，Shanghai 200444，China）

Based on the matrix Lie super algebra and supertrace identity，the integrable super-Geng hierarchy with self-consistent is established.Furthermore，we establish the infinitely many conservation laws for the integrable super-Geng hierarchy.The methods derived by us can be generalized to other nonlinear equation hierarchies.

supertrace identity；self-consistent sources；conservation laws；super-Geng hierarchy

2000 MR Subject Classification：35Q51

Article ID：1002—0462（2016）02—0201—10

Chin.Quart.J.of Math.

2016，31（2）：201—210

§1.Introduction

Soliton theory has achieved great success during the last decades，it is being applied to mathematics，physics，biology，astrophysics and other potential field［112］.The diversity and complexity of soliton theory enables investigators to do research from different views，such as Hamiltonian structure，self-consistent sources，conservation laws and various solutions of soliton equations.

In recent years，with the development of integrable systems，super integrable systems have attracted much attention.Many scholars and experts do research on the topic，and get lotsof results.For example，in［13］，Ma gave the supertrace identity based on Lie super algebras and its application to super-AKNS hierarchy and super-Dirac hierarchy and to get their super Hamiltonian structures.Afterwards，super C-KdV hierarchy［14］，super Boussinesq hierarchy［15］and super NLS-mKdV hierarchy［16］as well as their super Hamiltonian structures are presented. The binary nonlinearization of the super-AKNS system［17］and an implicit symmetry constraint，the Bargmann symmetry constraint［18］and binary nonlinearization of the super-Dirac systems were given.

Soliton equations with self-consistent sources have attracted considerable attention in recent research of soliton theory.Physically，the sources may result in solitary waves with a nonconstant velocity and therefore lead to a variety of dynamics of physical models.They are usually used to describe interactions between different solitary waves.Some results have been obtained by some authors［1921］.Recently，self-consistent sources for super G-J hierarchy［22］and super KN hierarchy［23］are presented.

The conservation laws play an important role in discussing the integrability for soliton hierarchy.An infinite number of conservation laws for KdV equation was first discovered by Miura，Gardner，and Kruscal in 1968［24］，then，lots of methods have been developed to find them［25-27］.

In this paper，starting from a Lie super algebra，an isospectral problems are designed.With the help of variational identity，Yang get super-Geng hierarchy and its Hamiltonian structure［28］. Then based on the theory of self-consistent sources，the self-consistent sources of super-Geng hierarchy is obtained by us.Furthermore，we present the conservation laws for the super-Geng hierarchy.

§2.A Super Soliton Hierarchy with Self-consistent Sources

Based on a well known super Lie algebra G［28］

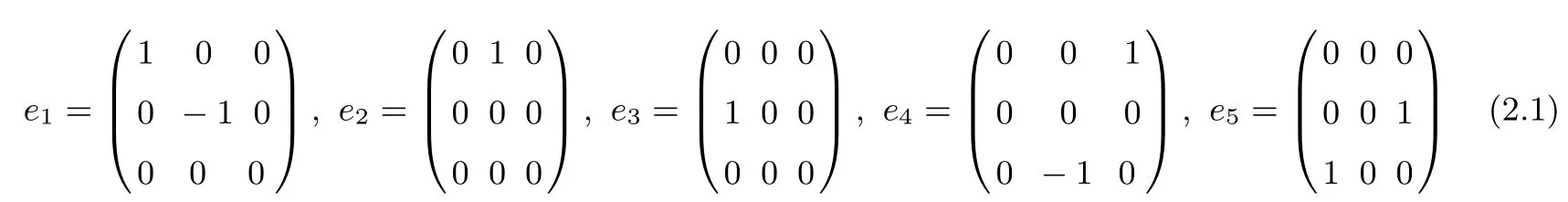
along with the communicative operation［e1,e2］=2e2,［e1,e3］=-e3,［e2,e3］=e1,［e1,e5］=［e4,e3］=-e5,［e1,e4］=［e2,e5］=e4,［e4,e4］+=-2e2,［e5,e5］+=2e2,［e4,e5］+=［e5,e4］+= e1.

Considering an auxiliary linear spectral problem

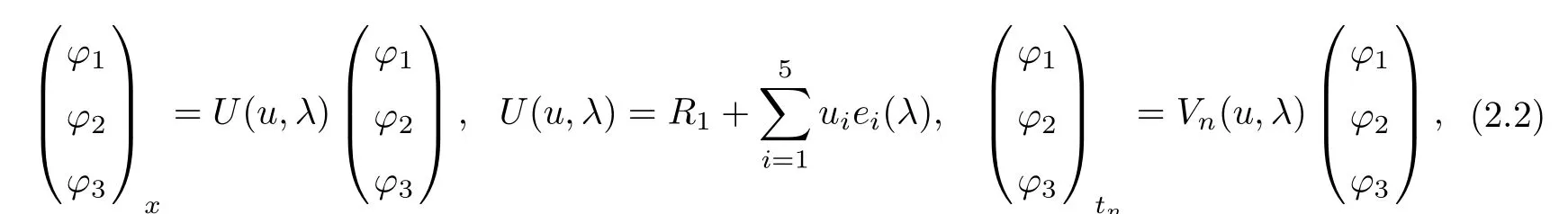
where u=（u1,···,us）T,Un=R1+u1e1+···+u5e5,ui（n,t）=ui（i=1,2,···,5）,ϕi=ϕ（x,t）are field variables defining on x∈R,t∈R；ei=ei（λ）∈˜sl（3）,R1is pseudoregular element.

The compatibility condition gives to the zero curvature equation

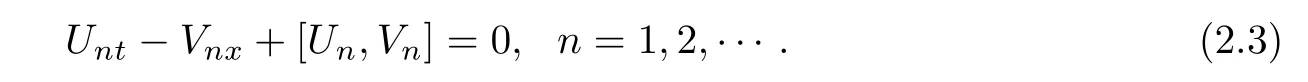
If an equation

can be worked out through Eq（2.3），we call Eq（2.4）a super-evolution equation.If there is a super-Hamiltonian operator J and a function Hnsuch that

where

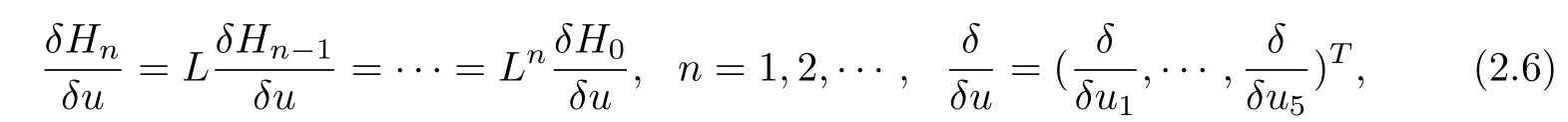
then Eq（2.4）posses a super-Hamiltonian equation.Thus，we called Eq（2.4）has a super-Hamiltonian structure.

According to the Eq（2.2），now we consider a new auxiliary linear problem.For N distinct λj,j=1,2,···,N，the systems of（2.2）become into the following

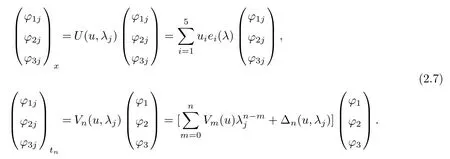
Based on the result in［29］，we can show that the following equation

where αjare constants.Eq（2.8）determines a finite-dimensional invariant set for the flows（2.6）.

For（2.7），it is known that

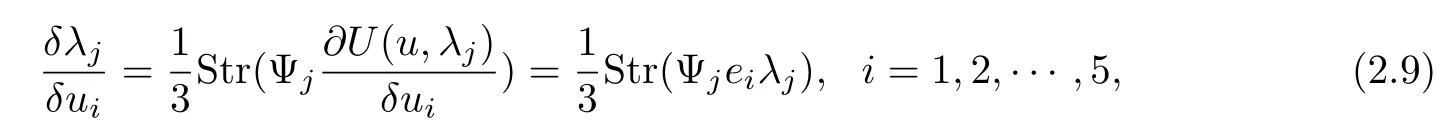
where Str denotes the trace of a matrix and

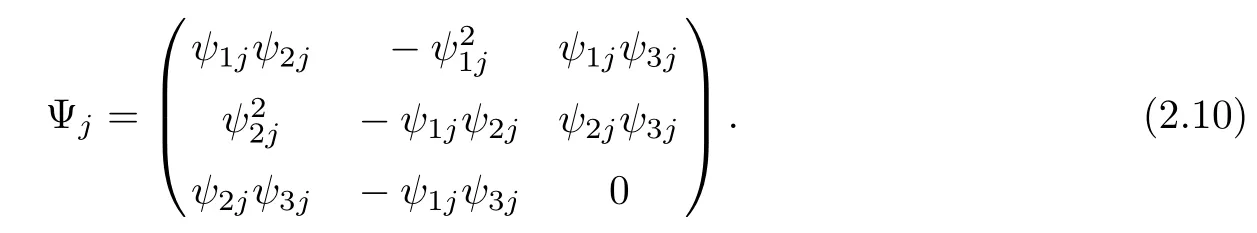
From the Eqs（2.8）and（2.9），a kind of super Hamiltonian soliton equation hierarchy with self-consistent sources is presented as follows

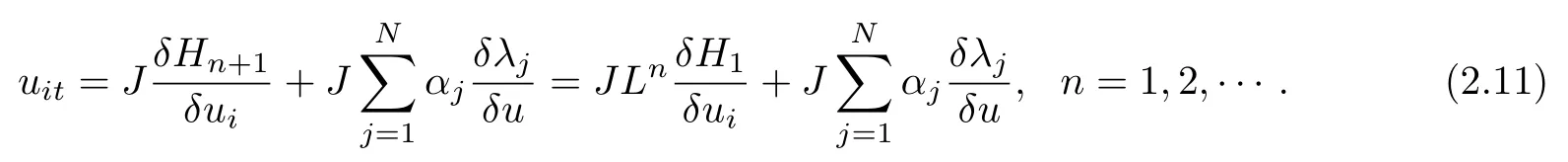
§3.The Super-Geng Hierarchy with Self-consistent Sources

It is known that the hierarchies of the Geng equations are presented in［30］and the super-Geng spectral problem associated with the Lie super-algebra is given in［28］

where

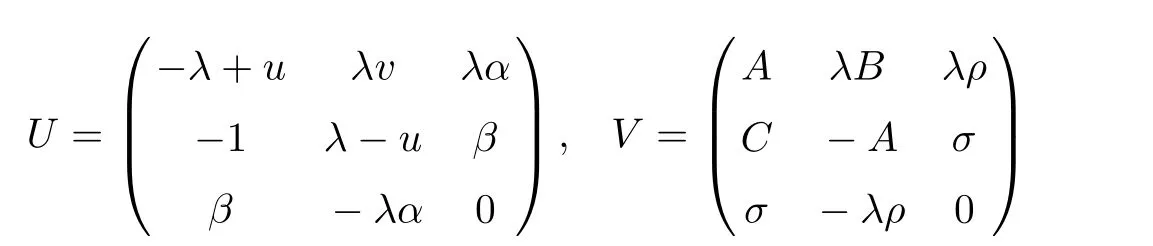
As α and β are fermi variables，they constitute Grassmann algebra. Starting from the stationary zero curvature equation

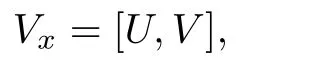
we have

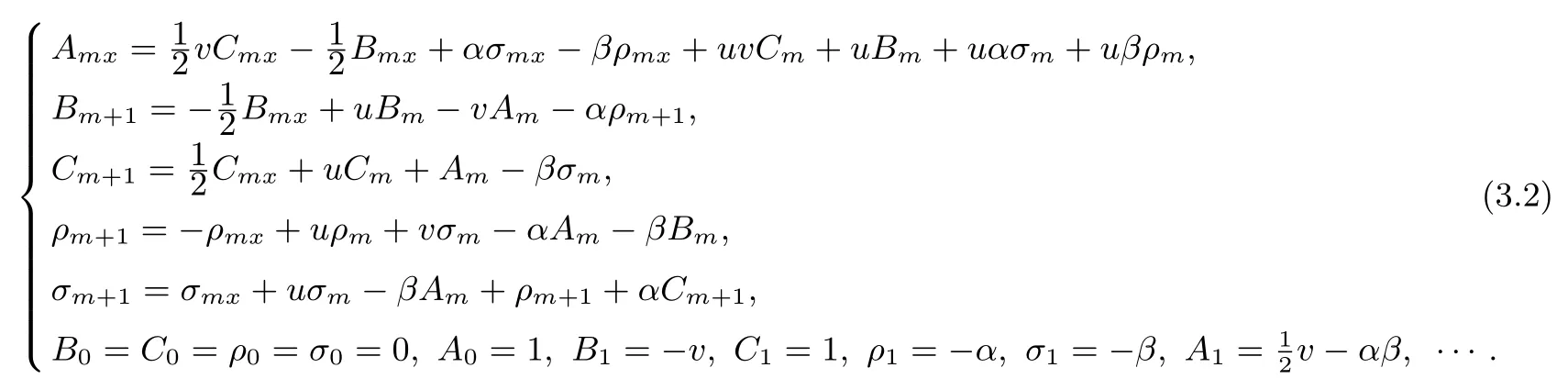
Then we consider the auxiliary spectral problem

where

Considering

substituting（3.4）into the zero curvature equation

We get the super-Geng hierarchy

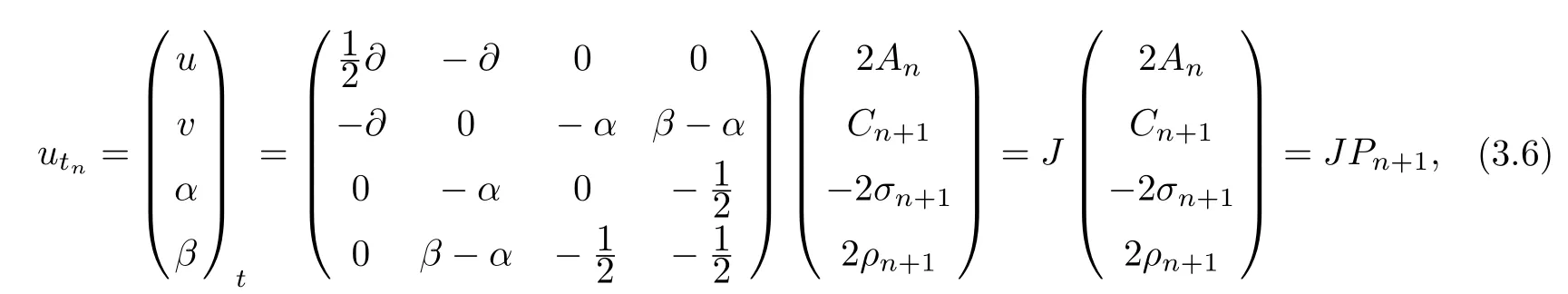
where

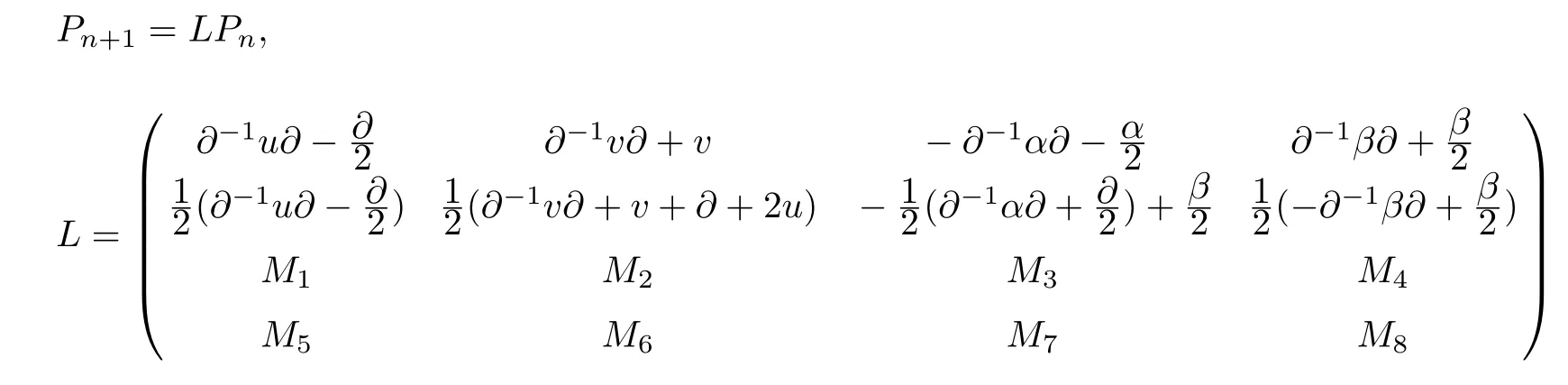
with

According to super trace identity，a direct calculation reads

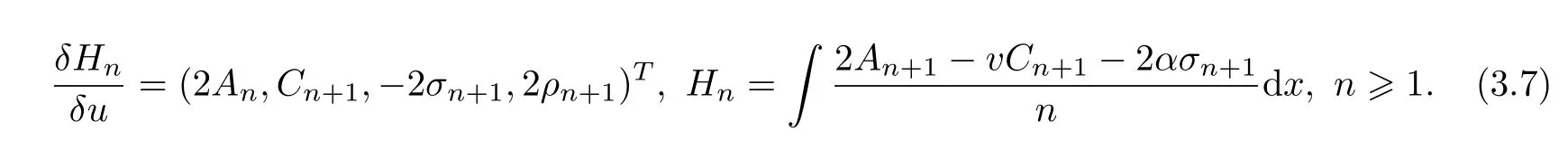
When we take n=2，the hierarchy（3.6）can be reduced to the super equations

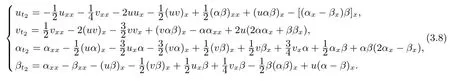
Next，we will construct the super-Geng hierarchy with self-consistent sources.Considering the linear system

From Eq（2.8），for the system（3.1），we set

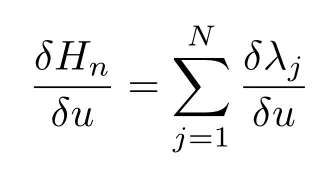
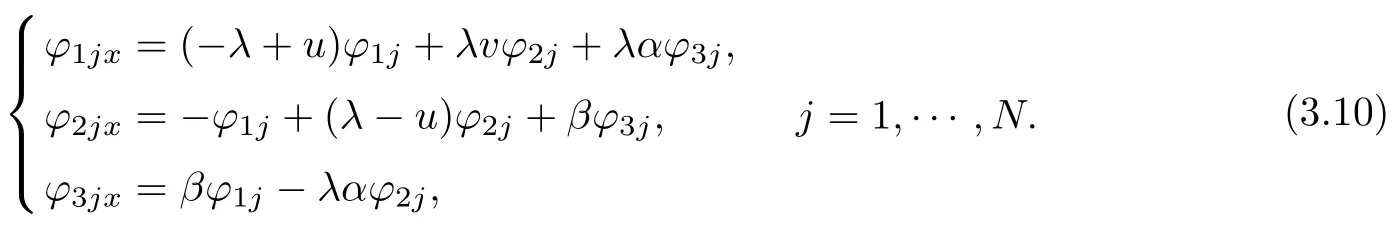
According to（2.11），the integrable super-Geng hierarchy with self-consistent sources is proposed

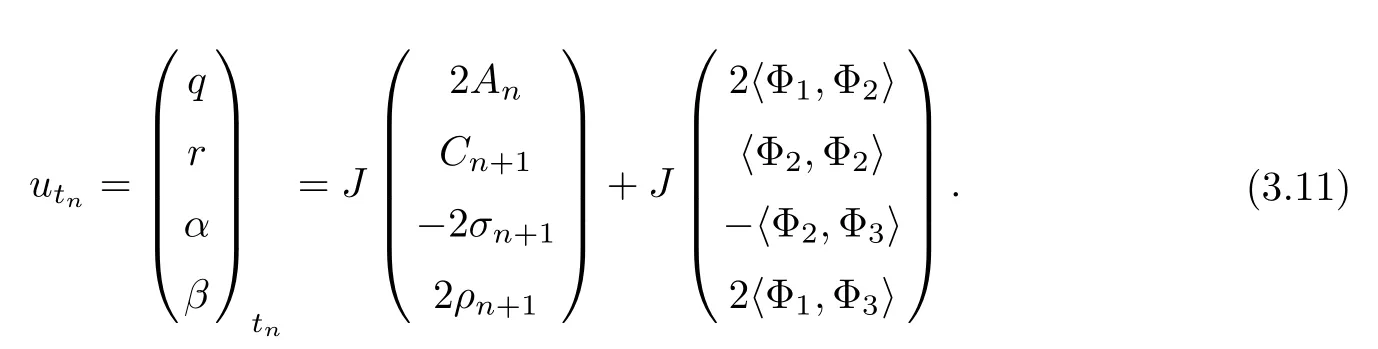
When n=2，we obtain the super-Geng equation with self-consistent sources

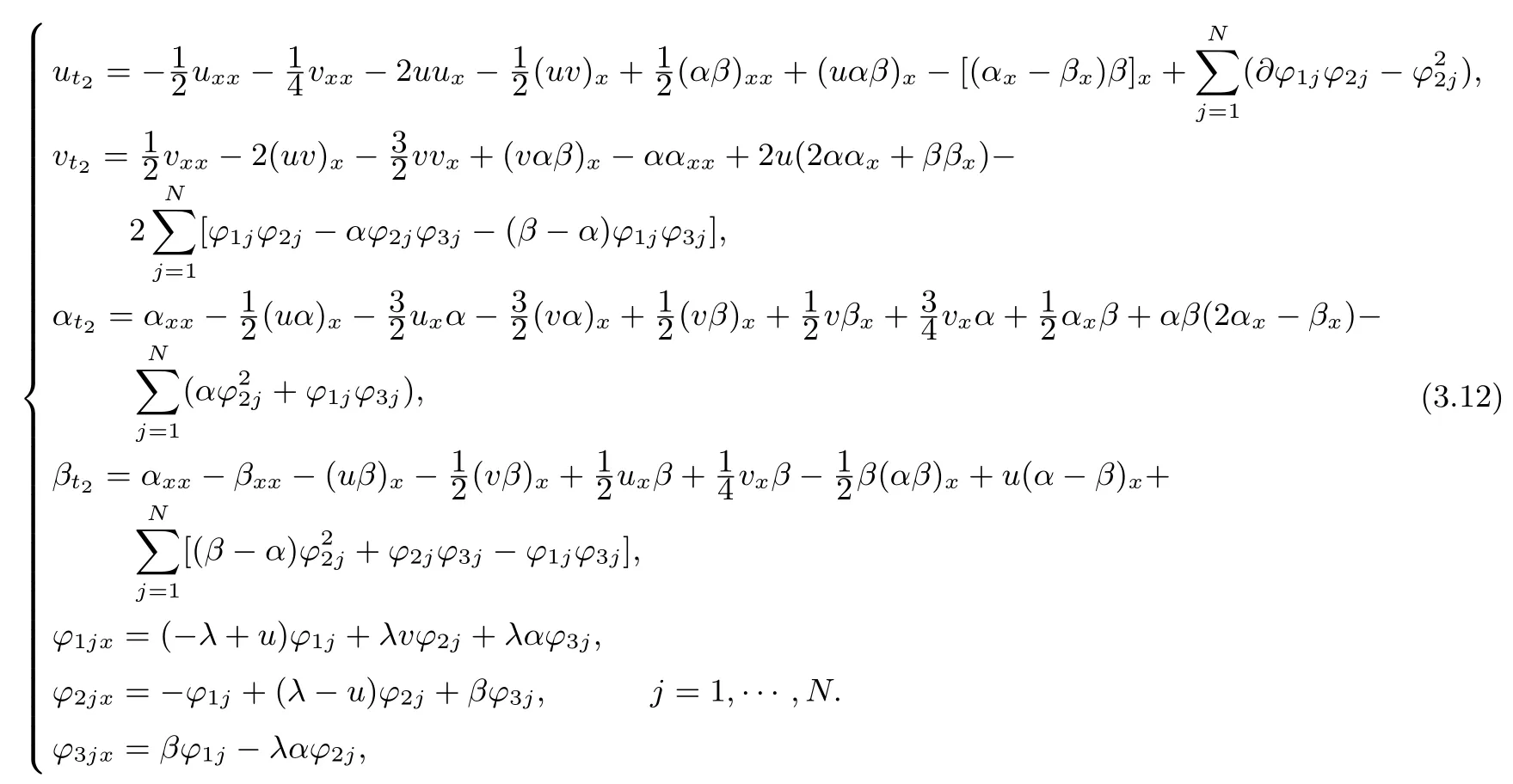
§4.Conservation Laws for the Super-Geng Hierarchy

In the following，we will construct conservation laws of the super-Geng hierarchy.Introducing two variables From Eq（2.7）and Eq（3.1），we have

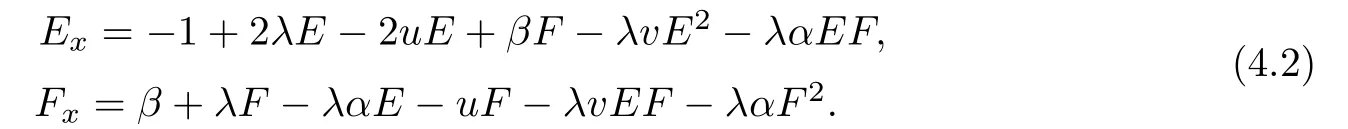
Expand E,F in the power of λ-1

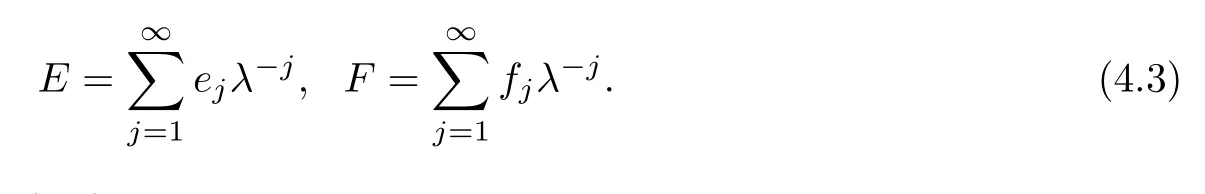
Substituting Eq（4.3）into Eq（4.2）and comparing the coefficients of the same power of λ，we obtain

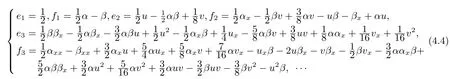
and a recursion formula for enand fnare given

It is easy to calculate that

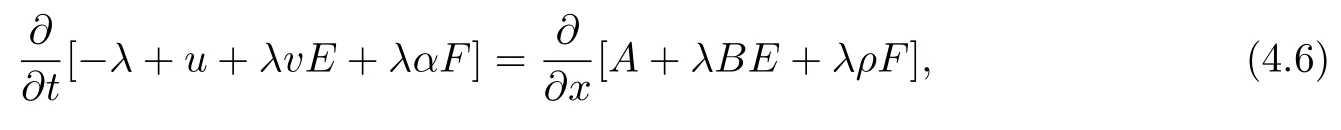
where

In order to obtain the conservation laws for the super-Geng hierarchy，we define

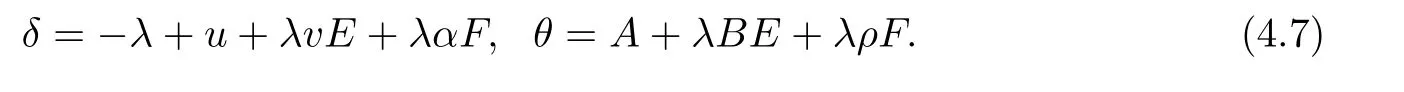
Then the Eq（4.6）can be written as δt=θx，which is just the formal definition of conservation laws.We expand δ and θ as series in powers of λ with the coefficients，which are called conserved densities and fluxes respectively

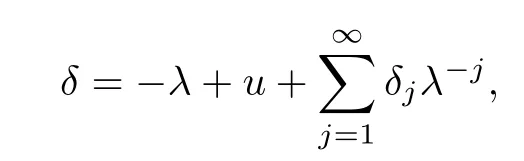
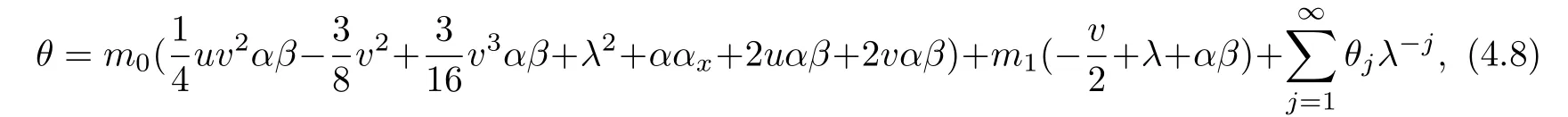
where m0,m1are constants of integration.The recursion relation for δnand θnare

where enand fncan be calculated from Eq（4.6）. The first conserved densities and fluxes are read

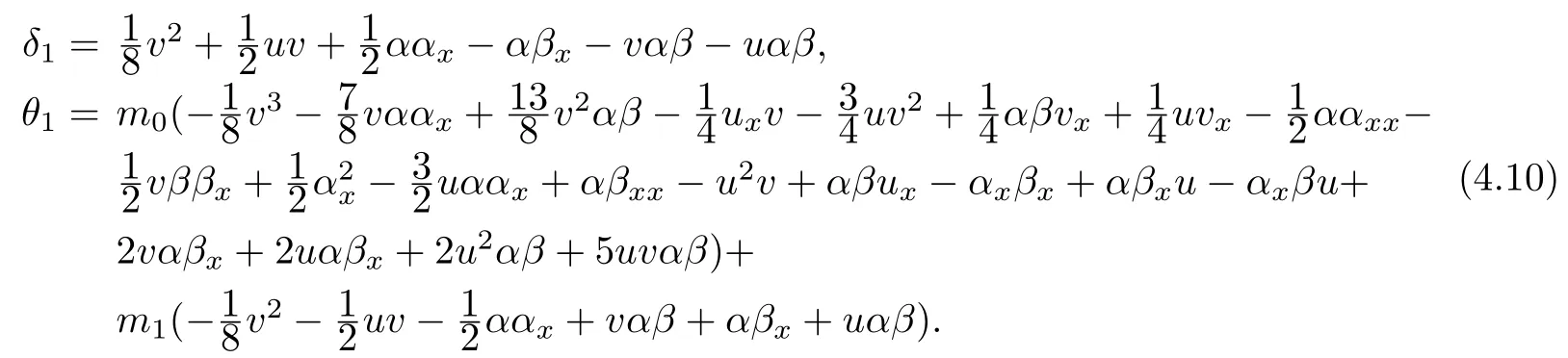
Thus，we obtained the infinitely many conservation laws of super-Geng equation hierarchy.

§5.Conclusions

Finding the integrable couplings of integrable systems is always an important part in soliton theory.With the help of variational identity，the Hamiltonian structure can also be presented. Based on Lie super algebra，the self-consistent sources of super-Geng hierarchy can be obtained. Finally，we also get the conservation laws of the super-Geng hierarchy.It is worth to note that the coupling terms of super integrable hierarchies involve fermi variables.In other words，the parameters in the coupling terms are fermi variables which is different from the ordinary one.

［References］

［1］KRUGLOV V I，PEACOCK A C，HARVEY J D.Exact solutions of the generalized nonlinear Schr¨odinger equation with distributed coefficients［J］.Physical Review E，2005，71（5）：056619.

［2］WAZWAZ A M.The variational iteration method for rational solutions for KdV，K（2，2），Burgers，and cubic Boussinesq equations［J］.Journal of Computational and Applied Mathematics，2007，207（1）：18-23.

［3］AMARAL R L P G，LEMES V E R，VENTURA O S.Gharge fluctuations in soliton-antisoliton systems without conjugation symmetry［J］.International Journal of Modern Physics A，2011，26（27）：4817-4830.

［4］VELDHUIS T T.Solitons in two-dimensional anti-de Sitter space［J］.International Journal of Modern Physics A，2010，25（2）：289-299.

［5］LOU Sen-yue，TONG Bin，HU Heng-chun，et al.Coupled KdV equations derived from two-layer fluids［J］. Journal of Physics A：Mathematical and General，2006，39（3）：513-527.

［6］YOMBAA M.A generalized auxiliary equation method and its application to nonlinear Klein-Gordon and generalized nonlinear Camassa-Holm equations［J］.Physics Letters A，2008，372（7）：1048-1060.

［7］LOU Sen-yue，MA Hong-cai.Finite symmetry transformation groups and exact solutions of Lax integrable systems［J］.Chaos，Solitons Fractals，2006，30（4）：804-821.

［8］FAN En-gui.Extended tanh-function method and its applications to nonlinear equations［J］.Physics Letters A，2000，277（4）：212-218.

［9］JIANG Xiao-wu，LI Zhu.Multi-component KN hierarchy and associated two integrable couplings as well as their Hamiltonian structure［J］.Chinese Quarterly Journal of Mathematics，2008，23（3）：415-422.

［10］ZHU Yun，YIN Li.The integrable in Liouville sense of a finite-dimensional Hamilton system［J］.Chinese Quarterly Journal of Mathematics，2011，26（1）：11-15.

［11］WEI Han-yu，TONG Yan-chun，XIA Tie-cheng.N-soliton solution for Hirota-Satsuma equation［J］.Chinese Quarterly Journal of Mathematics，2012，27（2）：270-273.

［12］WEI Han-yu，XIA Tie-cheng.A new nonlinear integrable couplings of Yang equations hierarchy and its Hamiltonian structure［J］.Chinese Quarterly Journal of Mathematics，2014，29（2）：180-188.

［13］MA Wen-xiu，HE Jing-song，QIN Zhen-yun.A supertrace identity and its applications to superintegrable systems［J］.Journal of Mathematical Physics，2008，49（3）：033511.

［14］TAO Si-xing，XIA Tie-cheng.Lie algebra and Lie super algebra for integrable couplings of C-KdV hierarchy［J］.Chinese Physics Letters，2010，27（4）：040202.

［15］TAO Si-xing，XIA Tie-cheng.The super-classical-Boussinesq hierarchy and its super-Hamiltonian structure［J］.Chinese Physics B，2010，19（7）：070202.

［16］DONG Huan-he，WANG Xin-zeng.Lie algebras and Lie super algebra for the integrable couplings of NLSCMKdV hierarchy［J］.Communications in Nonlinear Science and Numerical Simulation，2009，14（12）：4071-4077.

［17］HE Jing-song，YU Jing，CHEN Yi，et al.Binary nonlinearization of the super AKNS system［J］.Modern Physics Letters B，2008，22（4）：275-288.

［18］YU Jing，HE Jing-song，MA Wen-xiu，et al.The Bargmann symmetry constraint and binary nonlinearization of the super Dirac systems［J］.Chinese Annals of Mathematics，2010，31B（3）：361-372.

［19］GE Jian-ya，XIA Tie-cheng.A New Integrable couplings of classical-Boussinesq hierarchy with self-consistent sources［J］.Communications in Theoretical Physics，2010，54（1）：1-6.

［20］YU Fa-jun.A kind of integrable couplings of soliton equations hierarchy with self-consistent sources associated with˜sl（4）［J］.Physics Letters A，2008，372（44）：6613-6621.

［21］XIA Tie-cheng.Two new integrable couplings of the soliton hierarchies with self-consistent sources［J］. Chinese Physics B，2010，19（10）：10033.

［22］WANG Hui，XIA Tie-cheng.Conservation laws for a super G-J hierarchy with self-consistent sources［J］. Communications in Nonlinear Science and Numerical Simulation，2012，17（2）：566-572.

［23］WANG Hui，XIA Tie-cheng.Conservation laws and self-consistent sources for a super KN hierarchy［J］. Applied Mathematics and Computation，2013，219（10）：5458-5464.

［24］MA Wen-xiu，FUCHSSTEINER B.Integrable theory of the perturbation equations［J］.Chaos，Solitons Fractals，1996，7（8）：1227-1250.

［25］MA Wen-xiu.Integrable cuoplings of soliton equations by perturbations［J］.Methods and applications of analysis，2000，7（1）：21-56.

［26］MA Wen-xiu，STRAMPP W.An explicit symmetry constraint for the Lax pairs and the adjoint Lax pairs of AKNS systems［J］.Physics Letters A，1994，185（3）：277-286.

［27］BLUMAN G W，CHEVIAKOV A F，ANCO S C.Applications of Symmetry Methods to Partial Differential Equations［M］.London：Spring Press，2010：1-117.

［28］YANG Hong-xiang，DU Jun，XU Xi-xiang，et al.Hamiltonian and super-Hamiltonian systems of a hierarchy of soliton equations［J］.Applied Mathematics and Computation，2010，217（4）：1497-1508.

［29］TU Gui-zhang.An extension of a theorem on gradients of conserved densities of integrable systems［J］. Northeastern Math Journal，1990，6（1）：26-32.

［30］GENG Xian-guo.A Bargmann system and a Neumann system［J］.Acta Mathematica Scientia，1993，18A（1）：80-84.

O175.9Document code：A

date：2013-09-18

Supported by the National Natural Science Foundation of China（11271008，61072147，11547175）；Supported by the Science and Technology Department of Henan Province（152300410230）；Supported by the Key Scientific Research Projects of Henan Province（16A110026）；Supported by the Education Department of Henan Province（13A110101）

Biography：WEI Han-yu（1982-），male，native of Zhoukou，Henan，a lecturer of Zhoukou Normal University，Ph.D.，engages in solitons and integrable systems.