Likelihood Inference under Generalized Hybrid Censoring Scheme with Competing Risks

MAO Song，SHI Yi-min

（1.School of Economics and Management，Shanxi University，Taiyuan 030006，China；2.Department of Applied Mathematics，Northwestern Polytechnical University，Xi’an 710072，China）



Likelihood Inference under Generalized Hybrid Censoring Scheme with Competing Risks

MAO Song1，SHI Yi-min2

（1.School of Economics and Management，Shanxi University，Taiyuan 030006，China；2.Department of Applied Mathematics，Northwestern Polytechnical University，Xi’an 710072，China）

Statistical inference is developed for the analysis of generalized type-II hybrid censoring data under exponential competing risks model.In order to solve the problem that approximate methods make unsatisfactory performances in the case of small sample size，we establish the exact conditional distributions of estimators for parameters by conditional moment generating function（CMGF）.Furthermore，confidence intervals（CIs）are constructed by exact distributions，approximate distributions as well as bootstrap method respectively，and their performances are evaluated by Monte Carlo simulations.And finally，a real data set is analyzed to illustrate all the methods developed here.

generalized type-II hybrid scheme；competing risks；conditional moment generating function；bootstrap method；confidence intervals

2000 MR Subject Classification：62F12，62F30，62N01

Article ID：1002—0462（2016）02—0178—11

Chin.Quart.J.of Math.

2016，31（2）：178—188

§1.Introduction

Inference and optimal design of competing risks model had attracted extensive attention in the field of reliability engineering and medical studies since it was proposed by Cox［1］.Generally，it is supposed that the different risk factors are independent to avoid the problem of model identifiability［2］.Based on the above assumption，researches can be classfied into two casesincluding large sample size and small sample size.For example，Kim and Bai［3］considered constant stress accelerated life test with multiple competing risks modes，and presented inference results by expectation-maximum algorithm.Sarhan et al［4］analyzed competing risks data under progressively type-II censoring scheme with binomial removal.Cramer and Schmiedt［5］developed a Lomax competing risks model under progressively type-II censoring scheme and addressed the problem of optimal censoring schemes based on the Fisher information matrix. On the other hand，lots of papers focused on Bayes inference with competing risks when the sample size is small.Among these，Xu and Tang［6］adopted a Dirichlet prior distribution based Bayesian method to analyze a competing-failure model.Sreedevi and Sankaran［7］discussed competing risks data from the Bayesian framework.They presented a Bayes estimator under squared error loss function based on a gamma prior distribution.

Nevertheless，authors all neglect the latent fact that there may be missing data in the reliability test.Generally speaking，censoring is inevitable in the life test.It is known that conventional type-II censoring experiment may be hold for a long time，while we may observe no items failed in type-I censoring scheme.These schemes are infeasible from a practical point of view.In order to solve the problem，we employ generalized hybrid censoring test. Chandrasekar et al［8］including two types of schemes：generalized type-I hybrid censoring scheme as well as generalized type-II hybrid censoring scheme.Where，the former one must predetermine the least and most observed failure number，while the later ensure ones terminate the experiment within the specified time period.It is clear that the later one is more convenient for practical application.And readers can refer to［9］along with［10］for a further understanding of generalized hybrid censoring model.

Showing different with the former，this paper focus on the likelihood inference for the small sample size when the data is generalized type-II hybrid censored.It is organized as follows：In Section 2，we present general assumptions of the model and obtain the MLEs for unknown parameters.Then exact distributions for parameters are established through the use of CMGF in Section 3.In Section 4，Confidence intervals for parameters are constructed by exact distribution，approximate distribution and parametric bootstrap method respectively.And their performances are compared by Monte-Carlo simulations in Section 5.In Section 6，we also present a numerical example to illustrate the methods discussed above.And finally，some concluding remarks are given in Section 7.

§2.Model，Likelihood and Conditional MLEs

2.1Model and Data

Suppose that there are two different risk factors responsible for the failure of test units. And their lifetimes due to the two factors follow independent exponential distribution.Then its probability density function（PDF）and cumulative density function（CDF）are given by

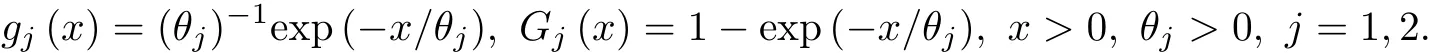
It is known that only the minimum of latent lifetime can be observed under competing risks

model.Let X=min｛X1,X2｝describe failure time of a unit，whose CDF and PDF are as

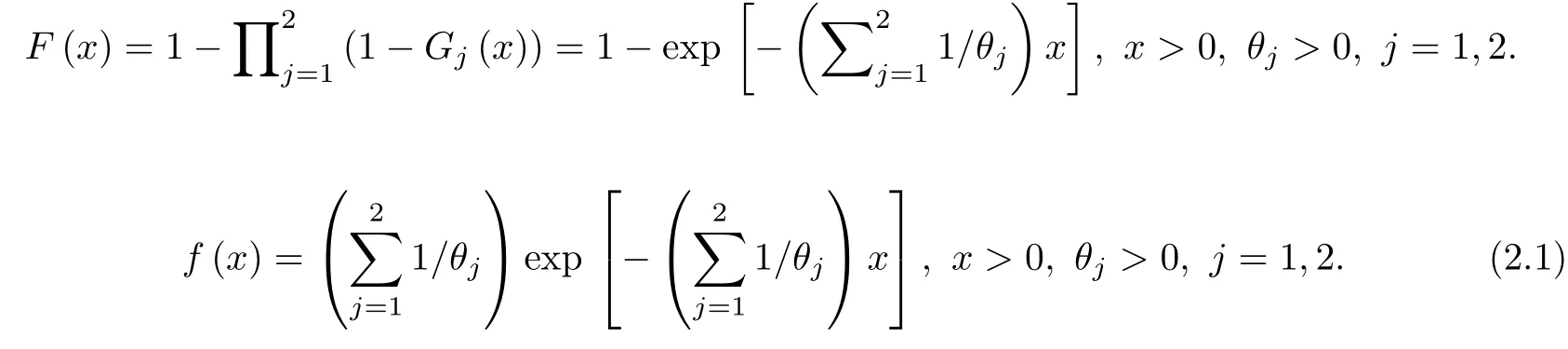
Furthermore，let Z describe the indicator for the failure factor，then the joint PDF of lifetimes and related failure factor（X,Z）is given by

Let（x1：n,x2：n,···,xn：n）describe lifetimes of n items in ascending order and let（z1,z2,···, zn）describe the indicator of risk factor corresponding to the sequential failure times.Here we express the ith failure item caused by risks factor 1 with zi=1,i=1,2,···,n.Apparently，zi=0 means that factor 2 is responsible for the ith failure.

Moreover，suppose that n identical items are simultaneously put on a life test in the presence of competing risks，and predetermine the censoring scheme（r,T1,T2）（T1＜T2）according to practical situation as well as historical data.Where，r denotes pre-determined failure number，（T1,T2）denotes pre-fixed experimental terminal duration.When the first item fails，record its lifetime x1：nand corresponding failure causez1.Continue with the experiment and record relative information just as before until the pre-fixed time τ0=（xr：n∧T2）∨T1，where，α∨β= max（α,β）,α∧β=min（α,β）.

For convenience，let Didenote the numbers of observed failures until Ti,i=1,2.Then under a generalized type-II hybrid censoring model，the observed experimental data can be classified into following cases

（a）0＜x1：n＜···xr：n＜···＜xD1：n≤T1,if xr：n＜T1＜T2；D1=r,r+1,···,n.

（b）0＜x1：n＜···＜xD1：n＜T1＜xD1+1：n＜···＜xr：n,if T1＜xr：n＜T2；D1= 0,1,···,r-1；D2=r,···,n.

（c）0＜x1：n＜···＜xD1：n＜T1＜xD1+1：n＜···＜xD2：n＜T2,if T1＜T2＜xr：n；D2= 2,3,···,r-1.

We can easily obtain the marginal probability in Case（a）and Case（c）as

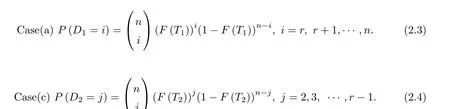
Similarly，the joint probability mass function（PMF）of D1,D2in Case（b）is as follows

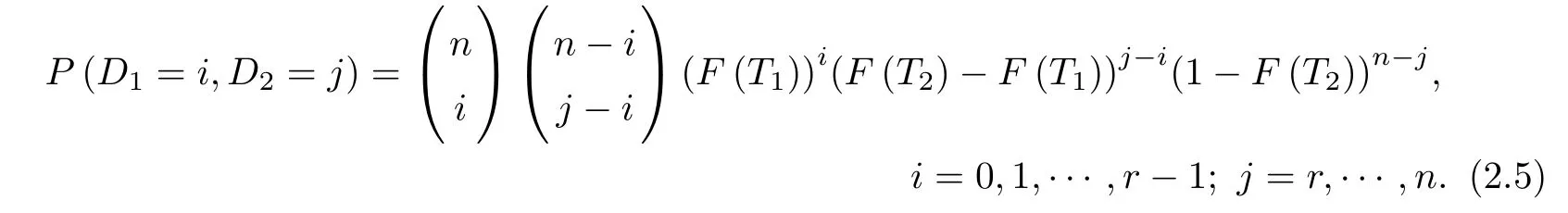
It is immediate to obtain the marginal PMF of D1in Case（b）as

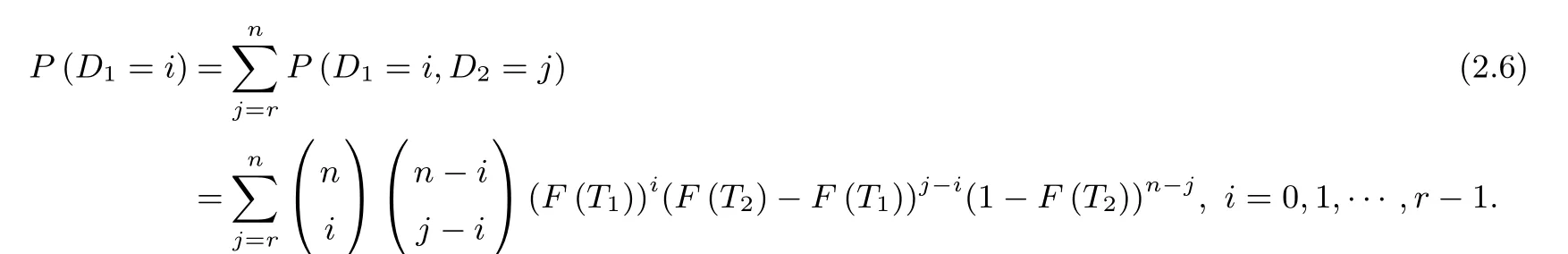
We also denote the total number of units that fail due to the risk factor j up to τ0by nj,j=1,2，then it is easy to obtain

2.2Likelihood and Conditional MLEs

Based on the observable data described above，the likelihood function is

L（θ|data）

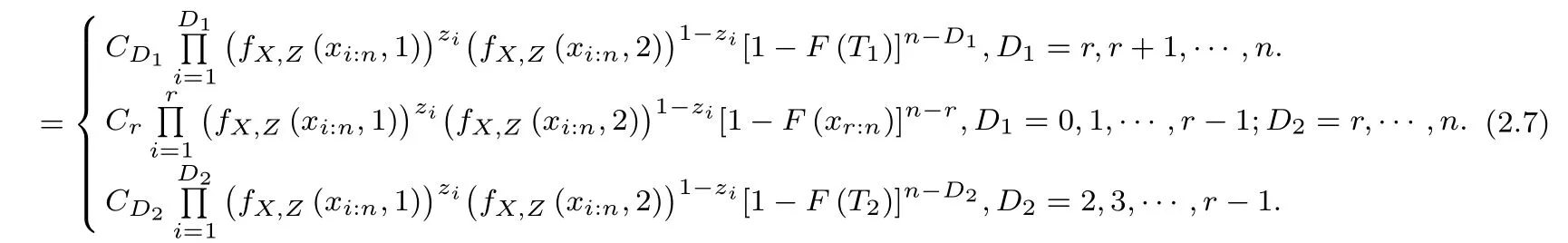
Where θ=（θ1,θ2）,Csis corresponding coefficient，Cs=n！/（n-s）！,s=（D2∧r）∨D1.

From（2.7），the MLEs of θjare easily obtained as

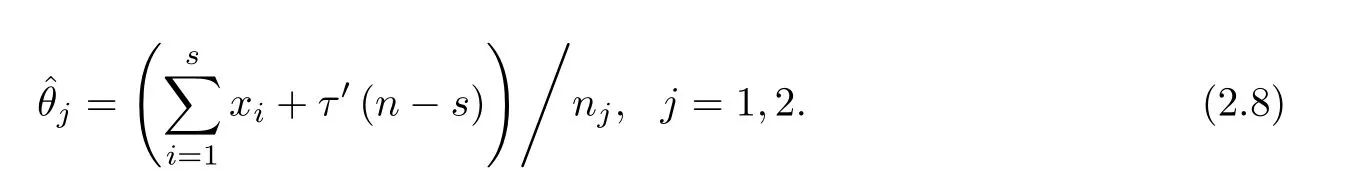
Noticing from（2.8），the MLEs of parameter θjdo not exist when nj=0,j=1,2.In order to estimate θj，we have to observe at least one failure caused by each risk factor.That is，ζ（s）=｛n1≥1,n2≥1,n1+n2=s｝,s=（D2∧r）∨D1.

§3.Exact Conditional Inference

Theorem 1Conditional on ζs，the moment generating function（MGF）ofˆθ1is given by

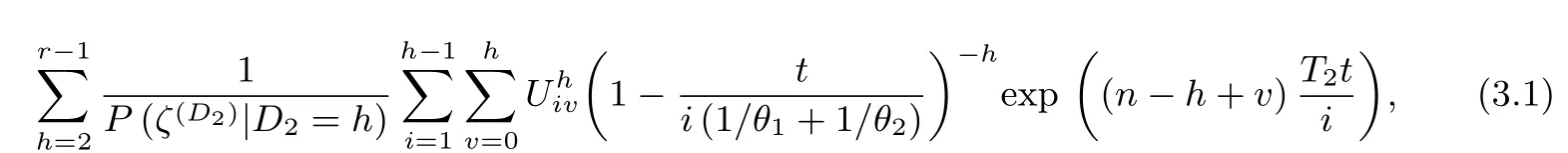
where， P

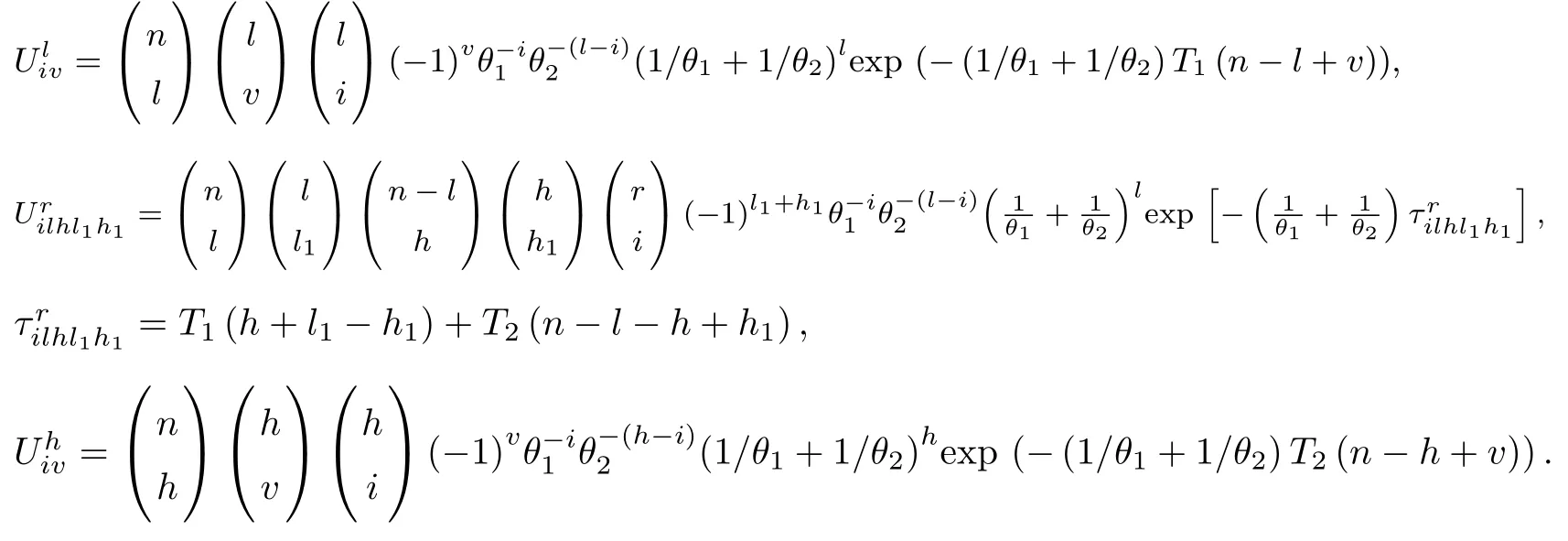
roof Conditional on ζs， we obtain

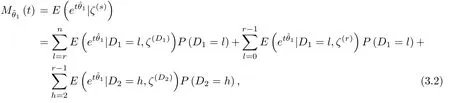
where P（D1=i）,P（D2=j）in above three cases can be obtained from（2.3），（2.4），（2.6）.

For convenience，let us denote the subset of indicator of failure causes as，where｛Zs=（z1,z2,···,zs）：zj=0,1；j=1,···,s；s=（D2∧r）∨D1｝.

For Case（a），conditional on D1=l,l=r,r+1,···,n；n1=i，we readily have the joint distribution of order statistics x1：n＜···＜xD1：n＜T1as

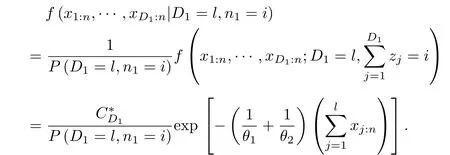
Then we can readily have

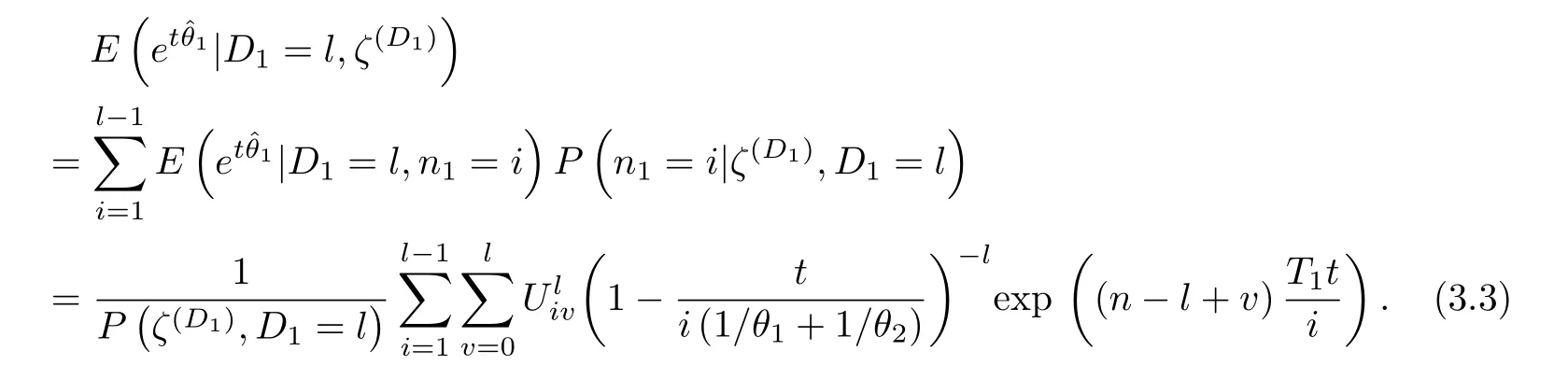
We can also obtain the joint PDF of order statistics x1：n＜···＜xD1：n＜T1＜xD1+1：n＜···＜xr：n，conditional on D1=l,l=0,1,···,r-1；n1=i in Case（b）as

Upon the conditional PDF obtained above，we can readily have

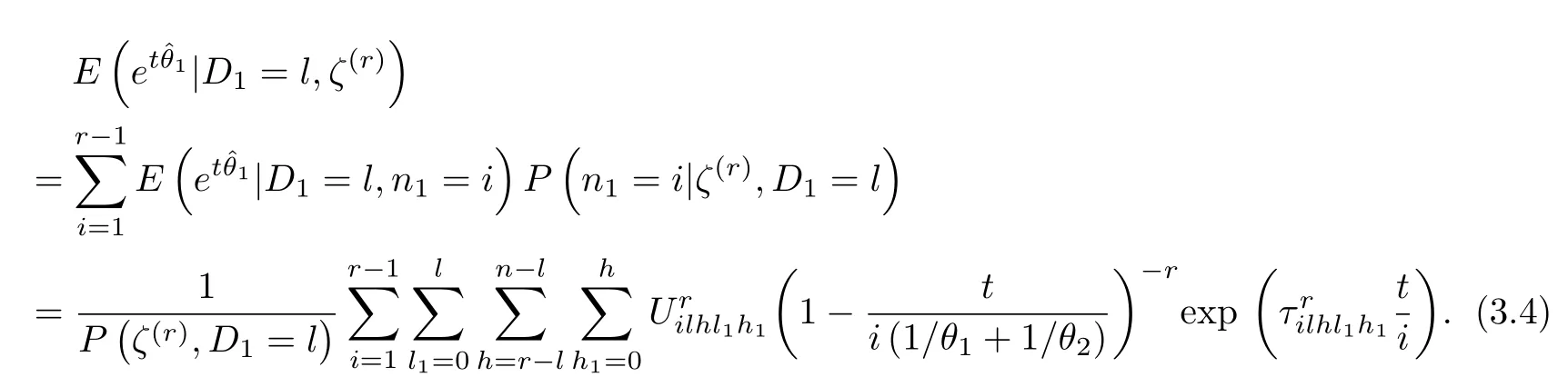
In order to obtain the results in last equation，we need to use the incomplete Beta integration and some basic repeated integration.

For Case（c），similarly，conditional on D2=h,h=2,3,···,r-1；n1=i，we readily have the joint distribution of order statistics x1：n＜···＜xD2：n＜T2as

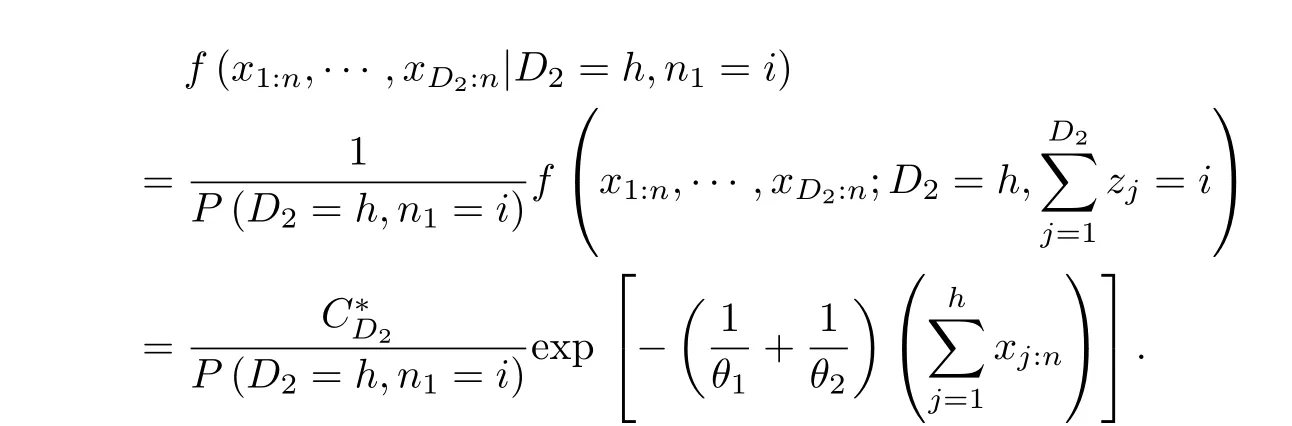
Then we can readily have

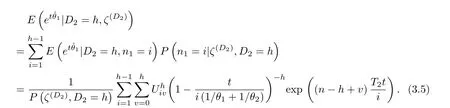
Then putting（3.3），（3.4）and（3.5）into（3.2），we can get the CMGF ofˆθ1as（3.1）shows.

Theorem 2Conditional on ζs，the MGF ofˆθ2is given by

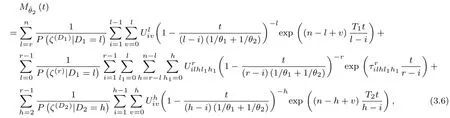
From Theorem 1，Theorem 2，we can immediately obtain the PDF ofˆθj,j=1,2，under generalized type-II hybrid censoring

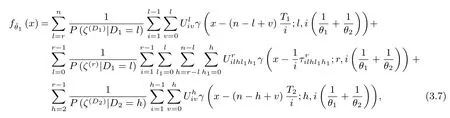
§4.Interval Estimation

4.1Exact Method

In this subsection，we construct CIs by conditional distribution of parameters obtained by CMGF.Firstly，we write the tail probability ofˆθjfrom（3.7），（3.8）as

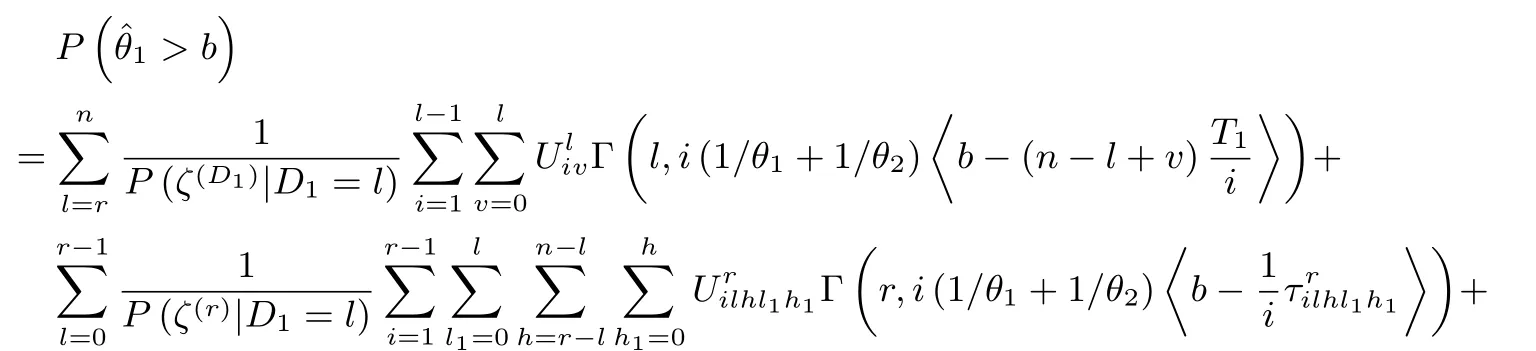
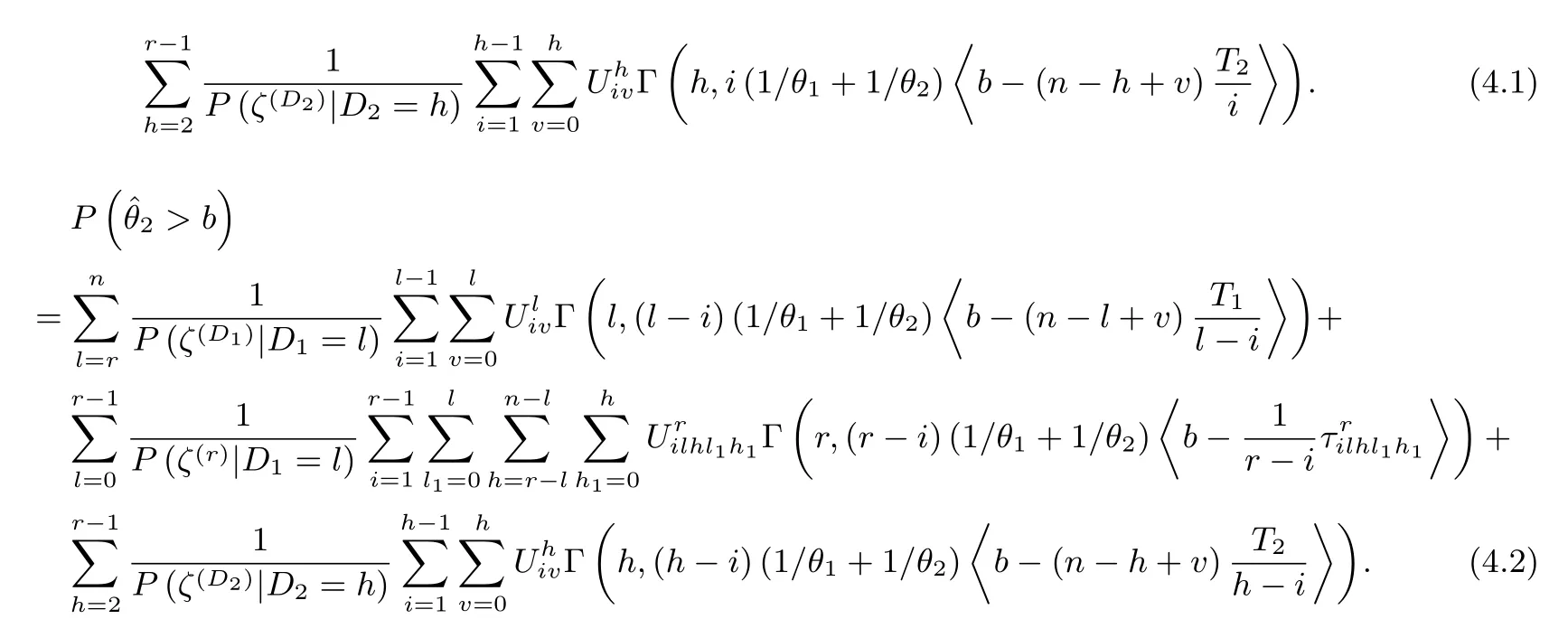
Here，bis arbitrary constant，〈x〉=max｛x,0｝,

4.2Approximate Method

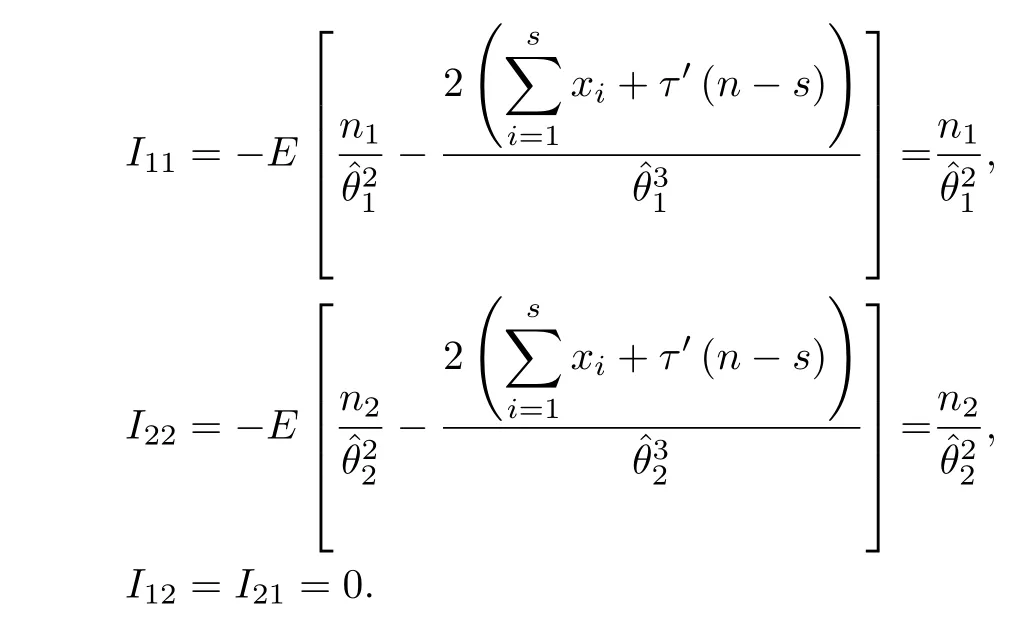
Moreover，variances ofˆθ1,ˆθ2can be described respectively as

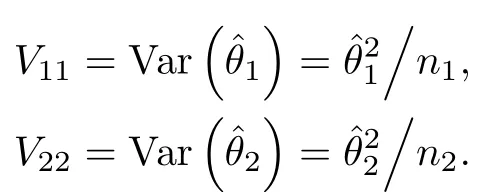
Based on asymptotic normality of MLEs，we can useas a pivot for θ1,θ2to establish two-sided 100（1-α）%approximate CI for θiaswhere zα/2is the quantile of the standard normal distribution.

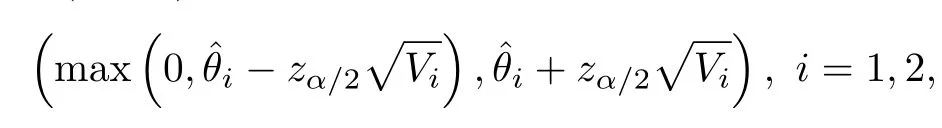
4.3Bootstrap Method

In this subsection，we obtain bootstrap CIs under the generalized type-II hybrid censoring scheme by the following algorithm.

Step 1Given the initial generalized type-II hybrid censoring sample，calculate the MLEs ˆθiof θi（i=1,2）unknown parameters from（2.8）.

Step 2Generate random exponential samples（U1,U2）of size n，where Ui～exp（θi）,i= 1,2.For each pair of（U1,U2），choose the minimum of two values along with the corresponding indicator as the simulated data（Xl,Zl）,l=1,···,n.Sort data｛X1,···,Xn｝in an ascending order and record competing risk factors in a corresponding manner.

Step 3Let｛X1,···,Xn｝denote order statistics of the data obtained above.If xr：n＜T1，find D1such that xD1：n＜T1＜xD1+1：n，then terminate the experiment at T1and set D1as the total failure number；If T1＜xr：n＜T2，then terminate the experiment at xr：nand set r as the total failure number；If T2＜xr：n，find D2such that xD2：n＜T2＜xD2+1：n，then terminate the experiment at T2and set D2as the total failure number.

Step 4With the simulated sample obtained above，calculate，the MLEs for unknown parameters θ=（θ1,θ2），from（2.8）.

Step 5Repeat steps 2～4 B-1 times，and sort all the values ofin an ascending order.Then we obtain the ordered bootstrap sample，where

Finally，two-sided 100（1-α）%bootstrap confidence interval for parameter θ=（θ1,θ2）is given by，such that

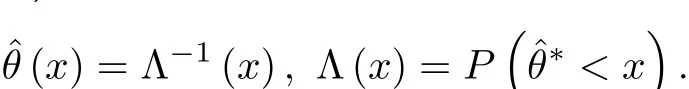
Here，Λ（x）denotes the CDF of parametersˆθ∗，Λ-1（·）denotes the inverse of the distribution Λ（x）.

§5.Simulation Studies

In order to judge the validity and efficiency of the approaches proposed in the previous sections，a Monte Carlo simulation was given under generalized type-II hybrid censoring test. We mainly adopted coverage percentages as an efficient measurement in performance assessment for CIs.In this simulation，the true value of parameters were chosen to be θ=（θ1,θ2）=（1,3）and θ=（θ1,θ2）=（2,5）respectively.Besides，we considered initial sample size as 20，40，80，120 and several different censoring schemes（T1,T2,r）.In each case，we presented various CIs based on 95%of the nominal level for small，medium and large sample sizes.And these results were presented in Table 1，Table 2，and Table 3，based on 1000 Monte Carlo simulations.

It is clear to see that exact method performs better than approximate method and bootstrap method generally in terms of coverage probabilities when n is no more than 40.The coverageprobabilities obtained by exact method are stable around the nominal level，while those by bootstrap method are slightly higher or lower than the true coverage probability of 95%.The possible reason for the poor performance of bootstrap method is that it sometimes undermines and other times overestimate the widths of CIs.Among the three methods，approximate approach presents the worst results for small and moderate sample size.This is mainly because the asymptotic normality of MLEs is significant on the ground of large amount of data.And it is also interesting to notice that the approximate coverage probabilities are almost same level for fixed parameter and sample size.We can also note from Table 1，Table 2 that estimated coverage probabilities for θ1are nearer to the given coverage probability than those for θ2by all three methods.The main reason for this is that we may observe more failure arising from risk factor 1 than factor 2 when θ1is smaller than θ2.

From Table 3，we can see that the two methods present a better performance when sample size is large.Generally，bootstrap method is more appropriate to analyze the data under generalized type-II hybrid censoring scheme.Another phenomenon we must state is that the estimated approximate coverage probabilities for θ2are not as good as those for θ1，but not so apparent in bootstrap case.However，when sample size is large，approximate method performs as well as（even better in some cases）bootstrap method.So，when sample size is larger enough，we should also try approximate method due to its computation ease and good performance.

§6.Illustrative Examples

In this section，we analyzed a real-life data set from［13］by proposed methods in Section 4. The data including ordered failure lifetimes and corresponding failure factors were presented in Table 4.Where‘Mode=0（or 1）'denotes the failure mode 0（or 1）responsible for the items failure.We chose the following censoring schemes

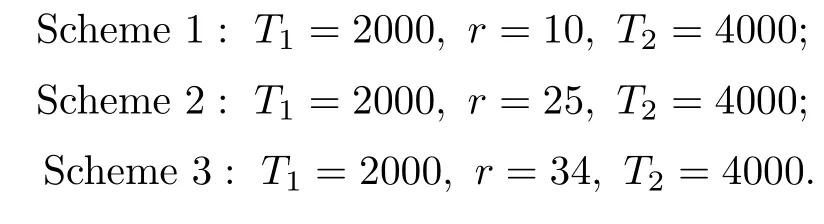
Based on the observed data and failure causes，we computed the conditional MLEs from（2.8），and the results were presented in Table 5.Where，n1was the total failure numbers due to the failure mode 1，and n2was the failure numbers due to failure mode 0.In Table 6，we constructed the CIs with true coverage probabilities of 95%by three different methods.

It is clear from Table 6 that the widths of CIs by bootstrap method are general wider than those of the other twos.So it is not surprising to find that bootstrap coverage probabilities usually hit higher than the true coverage probabilities.And it is also interesting to find that approximate CIs for parameters are sometimes narrower and other times wider than those of exact method，which may result in fluctuating coverage probabilities around the nominal level. Furthermore，all the methods provide wider CIs for parameter θ1than θ2in different schemes. The main reason for this is that we observe more failure numbers due to mode 0 than mode 1 in this example.As sample size grows，the width of CIs for parameter θ1decreases dramatically from 74619 to 6991，while that for parameter θ2decreases moderately at first，then increasesslightly.The possible explanation for this is that more failure items caused by risk mode 1 occur late in the test.

§7.Concluding Remarks

In this paper，we have considered inference of competing risks model for the analysis of exponential data when the data is generalized hybrid type-II censored.We have established exact distributions for parameters by CMGF and obtained corresponding exact CIs.We have also constructed CIs by approximate distribution and parametric bootstrap method.A numerical simulation has been conducted to evaluate the performances by the methods in the preceding section.We have also analyzed a real data set to illustrate those methods.The results show that exact method outperforms approximate method and bootstrap method when the sample size is small or medium.

［References］

［1］COX D R.The analysis of exponentially distributed life-times with two types of failure［J］.Journal of the Royal Statistical Society Series B（Methodological），1959，21（2）：411-421.

［2］CROWDER M J.Classical Competing Risks［M］.Boca Raton（FL）：Chapman and Hall，2010.

［3］KIM C，BAI D.Analyses of accelerated life test data under two failure modes［J］.International Journal of Reliability，Quality and Safety Engineering，2002，9（2）：111-125.

［4］SARHAN A M，ALAMERI M，AL-WASEL I.Analysis of progressive censoring competing risks data with binomial removals［J］.International Journal of Mathmatics Analysis，2008，2（20）：965-976.

［5］CRAMER E，SCHMIEDT A B.Progressively type-II censored competing risks data from Lomax distributions［J］.Computational Statistics and Data Analysis，2011，55（3）：1285-1303.

［6］XU An-chang，TANG Yin-cai.Nonparametric Bayesian analysis of competing risks problem with masked data［J］.Communications in Statistics-Theory and Methods，2011，40（13）：2326-2336.

［7］SREEDEVI E，SANKARAN P.A semiparametric Bayesian approach for the analysis of competing risks data［J］.Communications in Statistics-Theory and Methods，2012，41（15）：2803-2818.

［8］CHANDRASEKAR B，CHILDS A，BALAKRISHNAN N.Exact likelihood inference for the exponential distribution under generalized type-I and type-II hybrid censoring［J］.Naval Research Logistics，2004，51（7）：994-1004.

［9］PARK S，BALAKRISHNAN N.A very flexible hybrid censoring scheme and its Fisher information［J］. Journal of Statistical Computation and Simulation，2012，82（1）：41-50.

［10］BALARISHNAN N，KUNDU D.Hybrid censoring：models，inferential results and applications［J］.Computational Statistics and Data Analysis，2013，57（1）：166-209.

［11］CHILDS A，CHANDRASEKAR B，BALAKRISHNAN N，et al.Exact likelihood inference based on type-I and type-II hybrid censored samples from the exponential distribution［J］.Annals of the Institute of Statistical Mathematics，2003，55（2）：319-330.

［12］EFRON B.Computers and the theory of statistics：thinking the unthinkable［J］.SIAM Review，1979，21（4）：460-480.

［13］LAWLESS J F.Statistical Models and Methods for Lifetime Data［M］.Hoboken（NJ）：Wiley，2011.

O213.2Document code：A

date：2015-07-07

Supported by the National Natural Science Foundation of China（71401134，71571144，71171164）；Supported by the Natural Science Basic Research Program of Shaanxi Province（2015JM1003）；Supported by the Program of International Cooperation and Exchanges in Science and Technology Funded of Shaanxi Province（2016KW-033）；Supported by the Scholarship Program of Shanxi Province（2016-015）

Biographies：MAO Song（1987-），female，native of Linfen，Shanxi，a lecturer of Shanxi University，Ph.D.，engages in applied probability and statistics；SHI Yi-min（1952-），male，native of Xi'an，Shaanxi，a professor of Northwestern Polytechnical University，M.S.D.，engages in applied probability and statistics，reliability theory and application.