储层提前或滞后的矢量入靶井眼轨道优化

罗朝东，孙巧雷，王旭东，夏成宇，王大勇，杨　峰

（1.中石化西南石油工程有限公司钻井工程研究院，四川德阳618000；2.长江大学机械工程学院，湖北荆州434023）

储层提前或滞后的矢量入靶井眼轨道优化

罗朝东*1，孙巧雷2，王旭东1，夏成宇2，王大勇1，杨峰1

（1.中石化西南石油工程有限公司钻井工程研究院，四川德阳618000；2.长江大学机械工程学院，湖北荆州434023）

在钻定向井的过程中，按设计的具有井斜和方位变化的轨道钻进，若储层提前或滞后，就需要重新设计储层提前或滞后的轨道。针对这个问题，在满足现场工具造斜能力范围、靶点井斜控制范围和入靶点精度等情况下，建立了储层提前或滞后的井眼轨道优化的数学模型。从C#调用Matlab优化工具箱中求解多约束非线性多元函数最小值，从而建立储层提前或滞后的井眼轨道优化模块，计算储层终点改变后不同垂深各段的井眼曲率和各段的长度，指导现场设计钻具组合选取及判断是否需要上提钻杆。

储层提前滞后；轨道；优化设计；数学模型

在定向钻井［1］过程中，钻井的轨道是先期设计的，但是储层的位置往往具有不确定性。储层位置的不确性是指储层可能在水平方向和垂直方向上存在着一定的误差，即在钻进的过程中可能出现储层提前或者滞后的情形，因此需要实时监测实钻轨道，并在钻进的过程中，根据储层的位置及靶区形势［2-3］进行相应的钻进方案调整，对井眼的轨迹进行控制、对钻进的轨道进行优化设计［4-5］。

井眼轨迹控制是水平井钻井技术的关键环节［6］，国内外众多学者对钻井过程中井眼轨迹控制［7-9］的问题进行了探究，然而针对储层提前或滞后轨道优化的问题，并未建立起轨道优化的数学模型，笔者通过理论分析，建立了储层提前或者滞后轨道的钻井轨道目标函数和优化的计算模型，并通过具体算例进行了分析计算。

1　储层提前或滞后轨道优化理论模型建立

1.1建立坐标系与优化要求

在钻井过程中，储层的分布特点［10］是在水平方向尺寸大、垂直方向尺寸小，储层的提前或滞后主要考虑垂直方向的误差。在进行井眼轨道设计时，假定三段式井眼轨迹（造斜+微增+造斜）如图1所示，同时假定储层的位置和井眼方向是明确的，以P面水平方向位移为X，垂深为Z，建立二维坐标系O-XZ，由当前井底位置A和井眼方向是确定的，假定A点坐标为（XA，YA，ZA）、井斜角为αA。图中A为钻头现在所处位置，DM为储层提前或滞后当前靶点到储层顶界的垂深，MF为储层顶界到储存中间位置的距离（即储层厚度的一半），AC为优化轨道，S1为稳斜段，造斜率为Kα1；S2为微增斜段，微造斜率为Kα2；S3为造斜段，造斜率为Kα3；B、G、C处对应的井斜角依次为α1、α2、α3。

图1　轨道设计示意图

对于优化后设计的轨迹必须满足以下要求：

（1）对到达终点C的要求：C点到储层中间位置的距离小于微小量（即||F′F≤b1，如||F′F≤0.05m），确保接近储层中部。

（2）到达终点C的井斜角控制范围为（αDmin，αDmax）。

（3）优化轨道的各段造斜率在各段现场工具的造斜能力范围内（即Kαmin1≤Kα1≤Kαmax1，Kαmin3≤Kα3≤Kαmax3Kαmin2≤Kα2≤Kαmax2）

1.2建立目标函数

假设轨道的井斜变化率为Kαi，井身长为Si，则井眼轨迹的三维方程为：

通过对函数F′F（F′F为设计轨迹上的C点至靶点间的距离）的优化计算，求得在F′F足够小（如F′F＜0.05m）时的井斜变化率和段长等参数，进而可得到所求设计轨道。建立的目标函数是：寻找待钻井轨道长度S的最小值，即：

2　计算模型的建立

目前常见的三段式轨道形状包括造斜稳方位（Kα1≠0，Kφ=0）、微造斜段（Kα2≠0，Kφ=0）和造斜段（Kα3≠0，Kφ=0），下面将通过上述三段式轨道建立待钻井轨道最优化数学模型。

假设稳斜段长为S1，微造斜段长为S2，造斜段长为S3，造斜率为Kα1，微造斜率为Kα2，造斜率为Kα3。则C点的坐标应为：

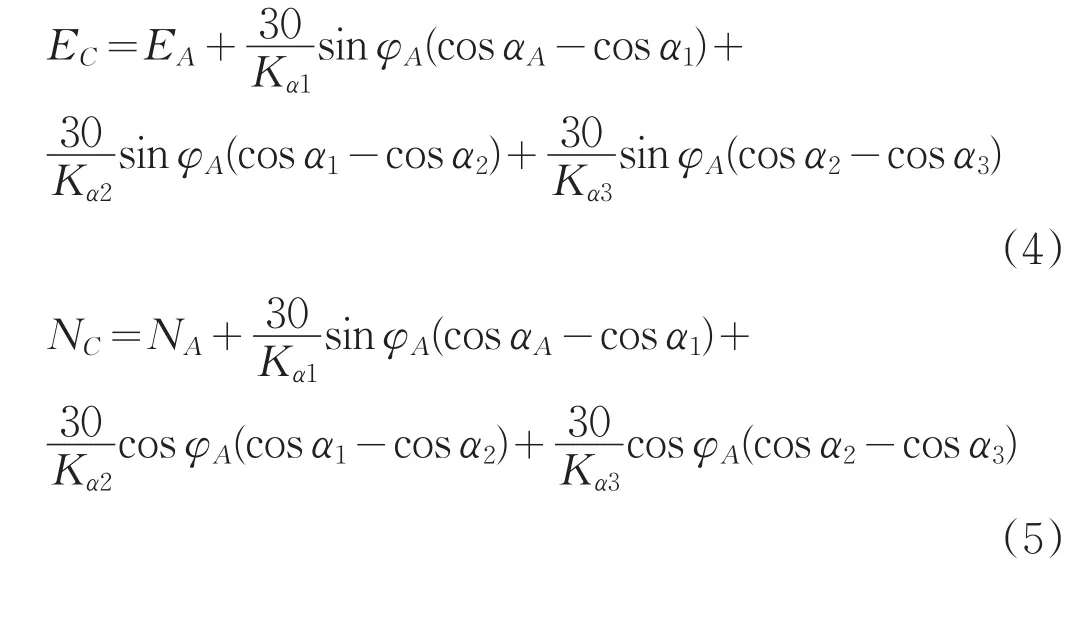
其中：

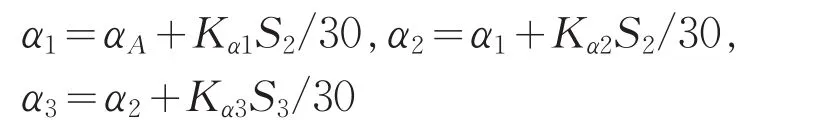
根据上述的设计准则，储层提前或滞后轨道设计的最优化数学模型（记为W）：

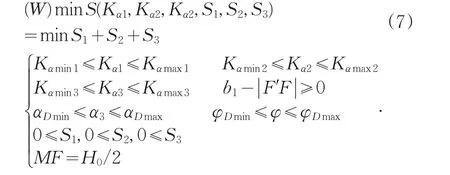
其中：

F′F=ZF-ZF'

b1为F′与F点间的距离精度控制常数，H0为储层厚度。通过对对上述模型（W）的优化计算，可得到满足所有约束条件下最优轨道的轨道参数。

3　实例计算

根据上述的优化模型，讨论储层改变后轨迹的优化。

3.1地层参数

四川盆地川西坳陷新场地区某井的井身数据为：井底井深为2725m，现井底A点坐标为E为23.5m，N 为-77m，垂深2206m，井斜为60°，方位为168°；由于储层提前导致储层顶界变为垂深2306m，储层厚度10m，优化设计待钻井眼轨迹。现场提供工具AB段造斜率Kα1增斜变化范围为（2°/30m，9°/30m）或降斜变化范围为（-5°/30m，-2°/30m），BG段的Kα2微增变化范围（2°/30m，3°/30m），GC段的Kα3造斜率（3°/30m，9°/30m），F′F精度为0.05m。靶点C处井斜角变化范围为（89.5°，90.5°），由（7）建 立 的6变 量S（S1，S2，S3，R1，R2，R3）优化模型为：

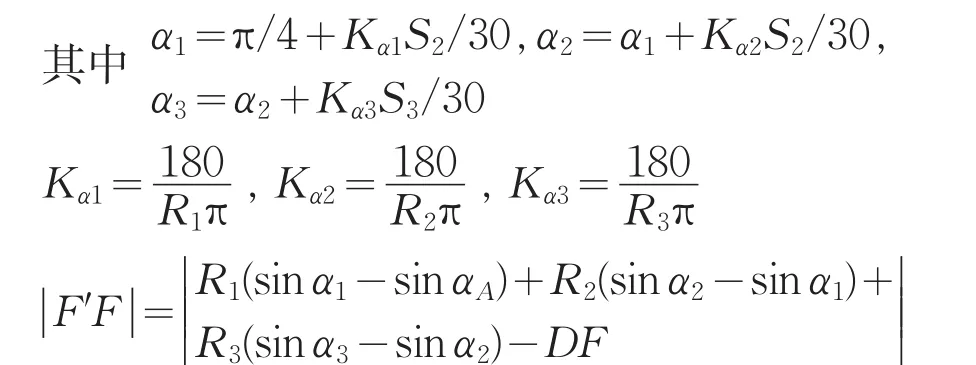
从C#调用Matlab建立井眼轨迹优化模块，通过这个模块计算得出上述井深相应的优化结果是：第一段的长为0；第二段采用稳斜，造斜率2°/30m，稳斜的长度为287.89m；第三段采用增斜，造斜率6.08°/30m，增斜的长度为287.89m，总长为338.71m。

3.2相关实例分析

以当前井底井斜角分别为60°和80°，储层厚度分别为10m和5m，讨论由于储层提前或滞后导致A点到储层顶界的垂深变化优化结果。

（1）井斜角60°、储层厚度为10m时，探顶角和优化后轨迹结果。

如表1所示，井斜角为60°、储层厚度为10m，当垂深超过100m时，选择降斜+稳斜+增斜的组合；当垂深不超过100m大于60m，选择稳斜+增斜组合；当垂深小于60m不低于30m，选择增斜+增斜组合；当垂深不超过20m，必须上提钻杆再入靶点。

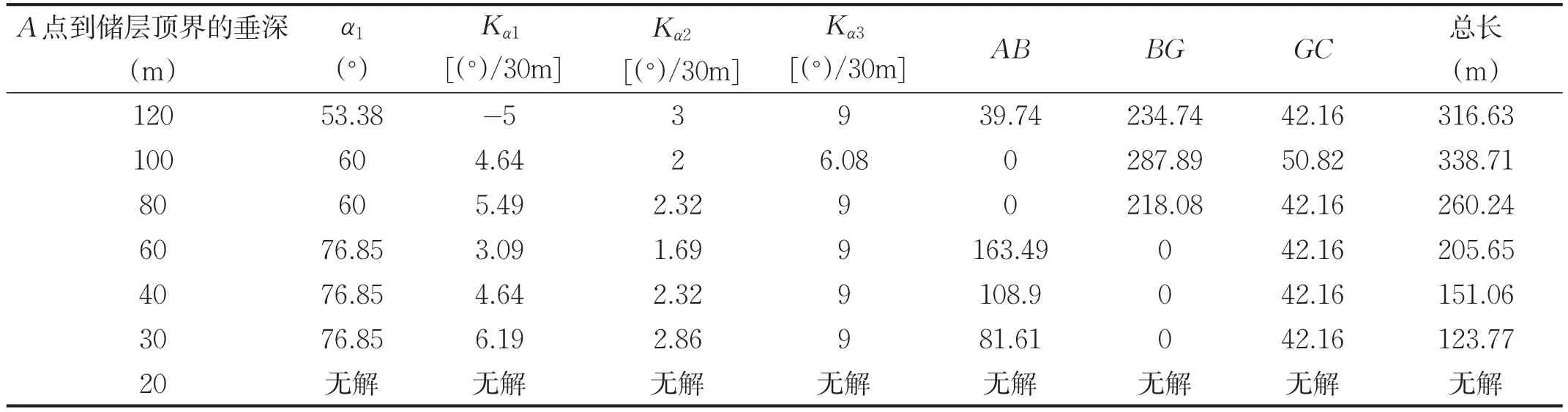
表1　不同垂深优化轨迹

（2）井斜角60°、储层厚度为5m时，探顶角和优化后轨迹结果。

如表2所示，井斜角为60°、储层厚度为5m，当垂深超过100m，选择降斜+稳斜+增斜的组合；当垂深不超过100m大于60m，选择稳斜+增斜的组合；当垂深小于60m不低于30m，选择增斜+增斜的组合；当垂深不超过20m，必须上提钻杆再入靶点。

（3）井斜角80°、储层厚度为10m时，探顶角和优化后轨迹结果。

如表3所示，井斜角为80°、储层厚度为10m，当垂深超过5m，选择降斜+稳斜+增斜的组合；当垂深不超过5m，选取稳斜+增斜或增斜的组合。

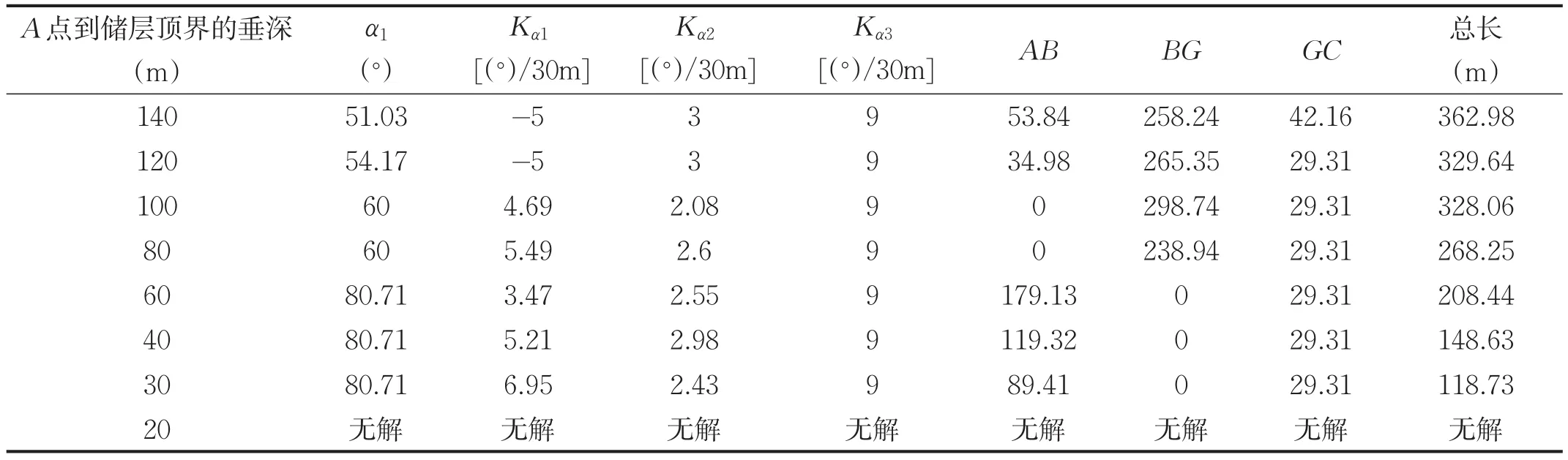
表2　不同垂深优化轨迹

（4）井斜角80°、储层厚度5m时，探顶角和优化后轨迹结果。

如表4所示，井斜角为80°、储层厚度为5m，当垂深超过10m，选择降斜+稳斜+增斜的组合；当垂深不超过10m大于1m，选择稳斜+增斜的组合；不超过1m和不低于0.5m.选择增斜+增斜的组合；小于0.5m必须上提钻杆。

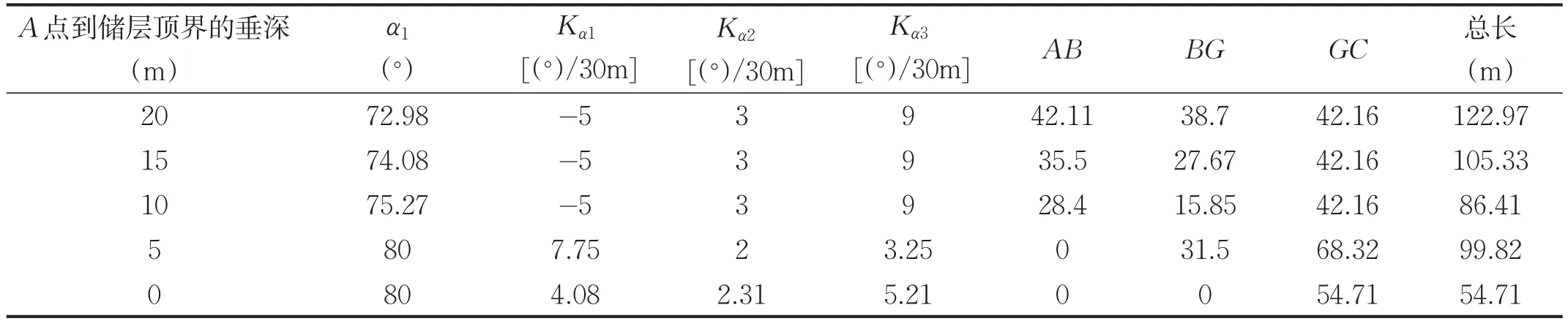
表3　不同垂深优化轨迹

表4　不同垂深优化轨迹

4　结论

（1）本文在满足井眼轨迹矢量和工具造斜能力要求的基础上，建立了储层提前或滞后轨道设计的最优化数学模型，解决了不同井斜和储层提前或滞后引起到储层顶界的垂深改变情况下轨道优化的问题。

（2）以60°和80°度为例，当储层滞后垂深过大和井斜角过大时，必须先降斜+微增+造斜，当储层滞后垂深很小和井斜角过大时，必须上提+微增+造斜。

［1］林琦，王鹏，刘振兴，章成强.定向施工中井眼轨迹控制［J］.中国井矿盐，2013（2）.

［2］隆东，张新刚，岳刚，向军文，胡汉月，刘志强.H024U井施工工艺及精确中靶技术措施［J］.探矿工程（岩土钻掘工程），2011 （3）.

［3］鲁港，夏泊洢，崔艳辉.水平井中靶分析的一种实用方法［J］.石油地质与工程，2011（6）.

［4］李增乐.中浅层水平井井眼轨道优化设计与现场施工［J］.探矿工程（岩土钻掘工程），2013（10）.

［5］相玉辉，屈展，陈军斌，王升廷，陈艺林.大位移井钻井工程优化设计与应用［J］.石油机械，2006（10）.

［6］杨晓峰，杜晶晶.井眼轨迹连续控制钻井技术研究与应用［J］.石油钻采艺，2012（1）.

［7］曹传文，薄珉.最小曲率法井眼轨迹控制技术研究与应用［J］.石油钻采工艺，2012（3）.

［8］侯喜茹，柳贡慧，汪志明，刘世昌.井眼轨迹控制系统特征描述及方法研究［J］.钻采工艺，2006（1）.

［9］王峰.侧钻双分支水平井井眼轨迹控制［J］.石油钻采工艺，2005（1）.

［10］黄根炉，赵金海，赵金洲，韩来聚.基于地质导向的水平井中靶优化设计［J］.石油钻采工艺，2004（6）.

［11］王鸿雁，肖文生，刘忠砚，姜立杰，田雪，王现锋.基于MAT⁃LAB的钻井井眼轨迹三维仿真研究［J］.石油矿场机械，2014 （4）.

TE921

A

1004-5716（2016）04-0083-04

2015-04-07

2015-04-09

国家自然科学基金项目（编号51405032）和湖北省自然科学基金创新群体（2012FFA033）联合资助。

罗朝东（1970-），男（汉族），云南昆明人，高级工程师，现从事定向井、水平井技术管理与科研工作。