基于架构的服务组合可靠性预测

黄鸿云，张　娟，丁佐华

(浙江理工大学，a.信息学院；b.理学院，杭州 310018)



基于架构的服务组合可靠性预测

黄鸿云a，张娟b，丁佐华a

(浙江理工大学，a.信息学院；b.理学院，杭州 310018)

软件可靠性是衡量软件质量的重要指标，而软件架构可以帮助预测软件的可靠性。为了研究基于服务组件架构的服务组合的可靠性计算，提出一种新的无需假设组件的失效是独立的可靠性计算方法。根据服务组件架构的端口执行情况构建Markov模型，并结合端口的失效数据来计算服务组合的可靠性。通过在线购物系统的可靠性计算论证方法的有效性。

服务组合；面向服务组件的架构；端口；可靠性；失效数据

0　引　言

在过去三十多年里，人们对软件可靠性的计算进行了较多的研究[1-9]，其中一种计算模型是基于架构的模型[5-9]。它不仅有助于基于组件的软件开发，同时还提供了一种可进行早期软件质量预测的方法。因此，可以利用软件架构来预测基于组件的软件的质量。例如，Chen等[5]提出了一种分析系统可靠性的模型，该模型适合具有不同架构层次的系统。此时，系统的可靠性分析依赖于组件的可靠性和不同层次间的连接器。此外，通过利用不同组件间的变迁概率来考虑操作剖面。但是他们要求假设组件和连接器的可靠性和变迁概率是相互独立的。单个组件的可靠性依赖于操作剖面和组件在系统的位置。系统可靠性的计算等价于组件执行路径的可靠性计算。执行路径的可靠性问题可以转化为一个基于组件的问题[6]。路径可靠性等于该路径上执行的组件的可靠性乘积。此时，可靠性的计算需假设组件间的失效是相互独立的以及接口的可靠性为1。Yacoub等[7]提出了一类关于基于组件的软件的可靠性模型和可靠性分析技术。为了分析系统的可靠性，他们利用组件间的交互场景构造称为组件依赖图(component-dependency graph，CDG)的概率模型。但是，CDG仅描述系统行为的序列模型，因此场景描述中的并发性质丢失了。

本文提出了一种新的计算面向服务组件架构(service component architecture，SCA)的服务组合的可靠性的方法。SCA的端口执行构成一个Markov链，端口映射为状态，则状态的可靠性即为端口的可靠性。于是，给定端口的失效数据即可在设计阶段预测系统的可靠性。另外，当系统在运行时，还可以获得实际失效数据。因此，所提方法能够从设计阶段到实施阶段提高系统的可靠性。一旦完成了组件的设计，同时也获得了可靠性计算公式；在实施之后，通过测试和失效密度分析，可以确定公式中个参数的具体值。该方法无需假设组件间的失效是相互独立的。

1　研究动机

Cheung[10]提出的基于组件的可靠性模型同时考虑了组件的可靠性和操作剖面，该模型使用描述系统行为的状态图。状态代表单个组件的执行，从一个状态到另一个状态的转移概率从系统的操作剖面获得。系统的可靠性依赖于状态的执行序列和单个状态的可靠性。

假设一个系统由3个组件构成，组件间的通信如图1所示。A、B为组件1的2个端口，C1、C2、S是组件2的3个端口，D、E是组件3的2个端口。组件1通过端口B将控制传递给组件2，组件2通过端口C2将控制传递给组件3，而组件3通过端口E将控制传递给组件1。

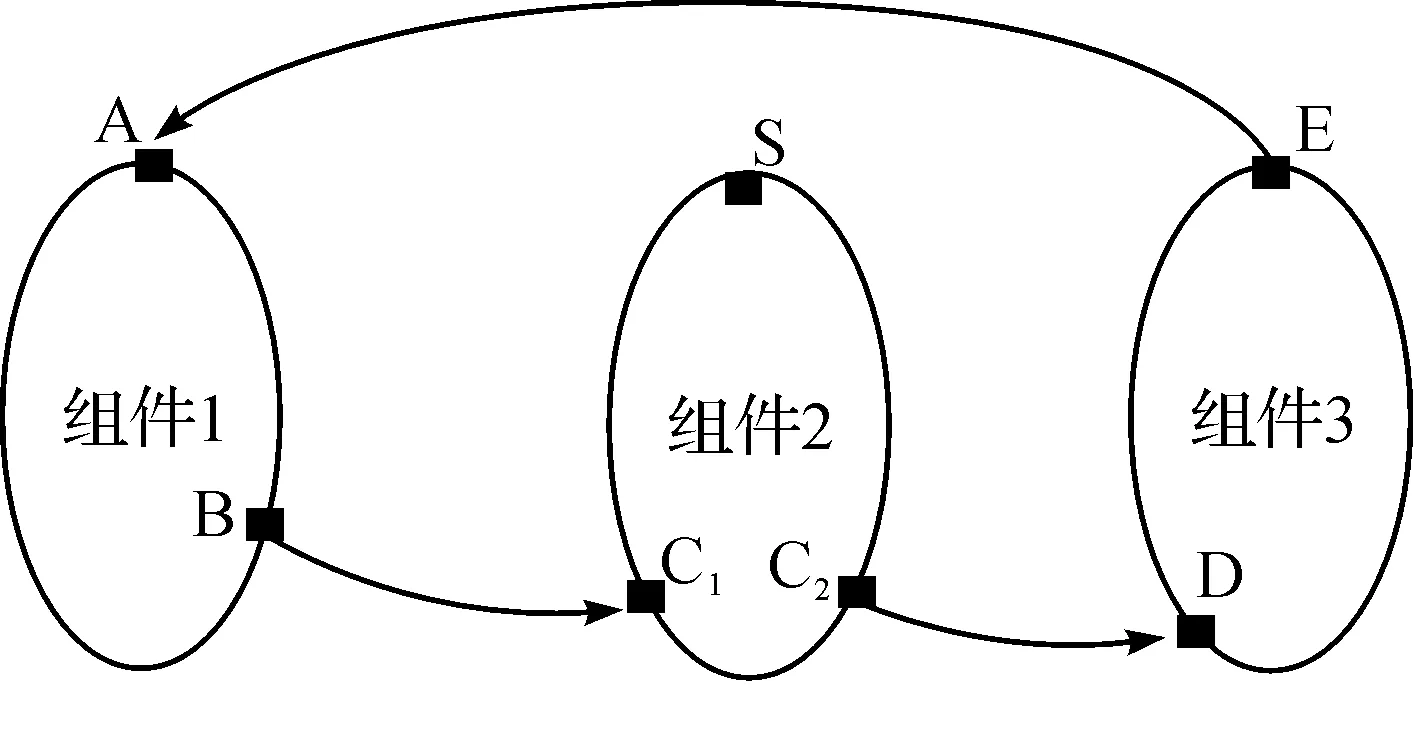
图1　具有3个组件的系统

在文献[11-12]提出的方法中，假设不同组件间的控制切换具有Markov性质，则组件架构可以用离散时间Markov链(discrete time markov chain，DTMC)进行建模，其中状态表示活动组件，有向弧表示控制的切换。图2(a)给出了上述系统的具有3个状态的Markov链。该方法将组件作为原子单元而忽略了端口间的交互。如果考虑端口的交互作用，则无需假设组件的失效是相互独立的，得到的Markov模型如图2(b)所示，它有6个状态。

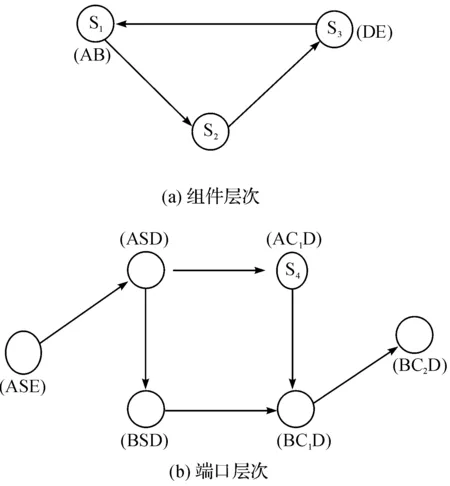
图2　组件架构到Markov链的映射

2　基于端口的组件模型

SCA模型[13]的提出使得基于服务的系统的实施变得更为容易，它提供一种定义和构建服务组件的方法，是诸如BPLE等服务组合语言的补充，使得开发者能够更加方便、有效地开发服务。但是SCA组装模型[13]缺乏形式化定义。因此，在以前工作中[14]，形式化定义了SCA模型。

定义1[14]：端口p是一个三元组(M，t，c)，M表示p中的有限方法集，t表示端口类型(provided或required)，c表示通信类型(同步或异步)。

定义2[14]：组件Com是一个四元组(Pp, Pr, G, W)，其中Pp是有限provided端口集；Pr是有限required端口集；G是有限子组件集合；W⊆TP×∪C∈G(C.Pp∪C.Pr)表示非自反的端口关系，其中TP=Pp∪Pr∪(∪C∈G(C.Pp∪C.P)r)，C.Pp和C.Pr分别表示子组件C的provided端口集合和required端口集合。

因为端口用来处理事件，因此可用端口活动来描述组件的动态行为。组件的动态行为表达式可定义为：BE::=

此表达式包含如下结构：序列化、选择、循环、并发和不确定。p·m表示端口p同步发送消息m，p1·mp2表示端口p1同步发送消息m给端口p2。BE[p1→p2]表示不同组件的端口的绑定操作，具体定义为：

其中⊙∈{·m,°m,◆m,◇m}。

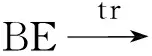
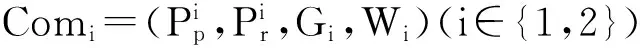
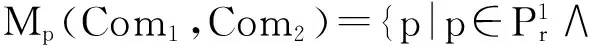
自动绑定集合定义为:

Mw(Com1,Com2)={(p1,p2)|p1∈Mp(Com1,Com2)∧p2=(p1.M,provided,p1.c)}。

于是，自动组合可定义为：

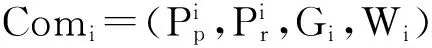
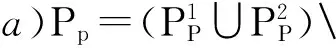
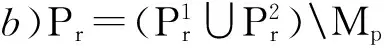
c)G=G1∪G2；

d)W=Mw∪{(p,p)|p∈Pp∪Pr}；

e)BE=(BE1▯BE2)[Mw]。

其中Mp和Mw分别是Mp(Com1,Com2)，Mw(Com1,Com2)的缩写。

显然，根据定义，两个组件的组合还是一个组件。

3　从SCA到Markov可靠性模型

3.1Markov模型

则整个系统的可靠性计算公式为：

R=T(1,n)×Rn,

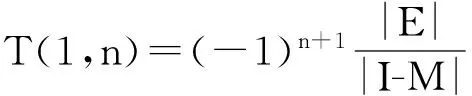
Cheung[10]提出的模型只有一个初始状态和一个终止状态。对于具有多个初始状态和多个终止状态的大型系统，可以通过在状态图中引入一个超初始状态和超终止状态将多初始状态多终止状态问题转化为单初始状态单终止状态问题。

定义4：有限状态机是一个5元组(Σ,S,s0,δ,F)，其中：

a)Σ是有限输入字符(有限非空符号集)；

b)S表示有限非空状态集；

c)s0表示系统的初始状态，s0∈S；

d)δ表示状态变迁函数，δ:S→S；

e)F表示终止状态集合，是S的一个字迹(可以为空)。

Markov链是这样一个有限状态机：每个变迁都附加了一个概率，且到下一个状态的转移概率仅依赖于当前状态。对于离散时间Markov链，变迁仅发生在离散时间间隔或离散事件，变迁概率服从离散分布。因此，离散时间Markov链包含：

a)n个状态组成的有限状态集合，S={s1,…,sn}；

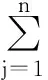
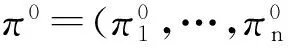
3.2从SCA建立Markov链的算法

根据端口的语义，可以通过计算SCA模型中所有的可达状态来建立有限状态机。下面给出了针对3个组件的组合的可达状态计算算法。令Com1、Com2、Com3为3个组件，它们对应的动态行为表达分别为BE1、BE2和BE3。

算法*注：本文只列出BE1和BE2间存在绑定的6种情况；事实上，绑定还可以在BE1和BE3之间，也可以在BE2和BE3间，故共有18种情况。：建立服务组合的可达状态

输入：Com1、Com2、Com3

输出：可达状态RS

Begin1Mw={p'→p″};ε=ϕ;i=1;j=1;k=12BE1=x1☉2☉…☉xn1☉;BE2=y1☉y2☉…☉yn2☉;BE3=z1☉z2☉…☉zn3☉3(BE1‖BE2‖BE3)[Mw]=BE1[Mw]‖BE2[Mw]‖BE3[Mw]=x1☉x2☉…☉xn1☉[Mw]‖y1☉y2☉…☉yn2☉[Mw]‖z1☉z2☉…☉zn3☉[Mw]=x1☉[Mw]x2☉[Mw]…xn1☉[Mw]‖y1☉[Mw]y2☉[Mw]…yn2☉[Mw]‖z1☉[Mw]z2☉[Mw]…zn3☉[Mw]4while(i<=n1&&j<=n2&&k<=n3)5 if(xi·m=p'&&yjm=p″)6 RS((BE1‖BE2‖BE3)[Mw])=RS(xi+1;…[Mw]‖yi+1;…[Mw]‖zk;zk+1;…[Mw])7 RS=RS→(xi,yj,zk)→{(xi+1,yj,zk)‖(xi,yj+1,zk)}8 i++;j++9 endif10 if(xi·m≠p'&&yjm=p″)11 RS((BE1‖BE2‖BE3)[Mw])=RS((xi·m[p'→p″]);(yjm;yj+1…[Mw]‖xi+1;…[Mw])‖zk;zk+1…[Mw]);12 RS=RS→{(xi,yj,zk+1)→};13 i++;j++;14 endif15 if(xi·m≠p'&&yjm≠p″)16 RS((BE1‖BE2‖BE3)[Mw]) =χ1(BE)RS((yjm;(yj+1…xi;…))[Mw]‖zk;…[Mw])+χ2(BE')RS((xi·m;(xi+1…‖yj;…))[Mw]‖zk;…[Mw]);BE=(yjm;(yj+1…‖xi;…))‖zk;…,BE'=(xi·m;(xi+1…‖yj;…))‖zk;…;17 i++;j++;18 endif19 if(xi◆m=p'&&yj◇m=p″)

20 RS((BE1‖BE2‖BE3)[Mw])=RS(xi◆m[p'→p″];xi+1[p'→p″];…‖yjm[p'→p″];yj+1[p'→p″];…‖zk; zk+1…[Mw]‖xi◆myj→yj◇mxi→[stop,ε/xi◆myj]21 RS=RS→(xi,yj,zk)→(xi+1,yj,zk)→22 i++;j++;23 endif24 if(xi◆m≠p'&&yj◇m=p″)25 RS((BE1‖BE2‖BE3)[Mw])= RS((xi◆m[p'→p″]);(yj◇m;yj+1…[Mw]‖xi+1;…[Mw])‖zk;zk+1…[Mw])‖26 RS=RS→(xi,yj,zk+1)→;27 i++;j++;28 endif29 if(xi◆m≠p'&&yj◇m≠p″)30 RS((BE1‖BE2‖BE3)[Mw]=χ1(BE)RS((yj◇m;(yj+1…‖xi;…))[Mw]‖zk;…[Mw])+ χ2(BE')RS((xi◆m;(xi+1…‖yj;…))[Mw]‖zk;…[Mw]); BE=(yj◇m;(yj+1…‖xi;…))‖zk;…,BE'=(xi◆m;(xi+1…‖yj;…))‖zk;…31 RS=RS→(xi,yj,zk)→(xi,yj,zk+1)→;32 i++;j++;33 endif34endwhileEnd

4　Markov可靠性模型的配置

根据上述算法，可以计算可达状态并建立有限状态机；但是，状态间的转移概率和各状态的可靠性还需要在后面通过测试进行配置。

4.1配置状态间的转移概率

在软件开发的后期，当测试或者领域数据可以使用时，组件轨迹可以通过分析工具获得，而测试覆盖工具用来获得一系列执行轨迹和变迁弧的频数。需要说明的是，每个变迁的概率必须包含轨迹的重复次数。

4.2配置状态的可靠性

两个服务的交互的特点包含如下3个属性：伙伴链接、端口类型以及操作。服务组合的后期绑定可以通过将服务的结束点分配给伙伴链接而获得。如果将服务看作是组件，则可以定义包含这3个属性的端口，如此对服务组合的测试实际上就是对端口交互的测试。于是，服务组合的可靠性依赖于端口的交互行为，或者端口可靠性。状态的可靠性可以通过下述方法进行计算。假设某个状态关联了端口集(p1,p2,p3)。在测试阶段可以获得端口p1,p2,p3的失效，所有这些失效合在一起就是该状态的失效。这也是和传统的状态的可靠性计算方法的不同之处。注意，本文考虑的是一个状态对应一个来自不同组件的端口的组合；如果一个状态有好几个不同的端口组合，则可用隐式Markov链计算系统的可靠性。

获取失效数据的方法之一是监测每个端口中变量的所有值，并判断这些值是否在预期的范围内。另一种方法是利用程序不变量，而程序不变量可以用Daikon工具获得，于是每个端口中“不好”的不变量就可以当作失效数据[15]。

5　实例分析

本文通过一个在线购物系统的例子来介绍所提出模型的使用。虽然该系统是一个简化的版本，但是它还是包含了如下结构：序列化、选择、循环和并行。

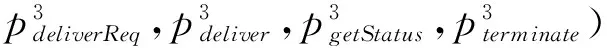
在实现时，首先创建组件，定义接口，然后将这些组件绑定到一起并用BPEL编辑器来实现。本文利用IBM WebSphere Integration Developer来开发BPEL的自主服务绑定。如此，在服务选择之后，服务绑定可以自动完成。通过将SCA模型映射为完整的J2EE应用包来部署应用，Java应用可由Tomcat和SQL数据库来实现。

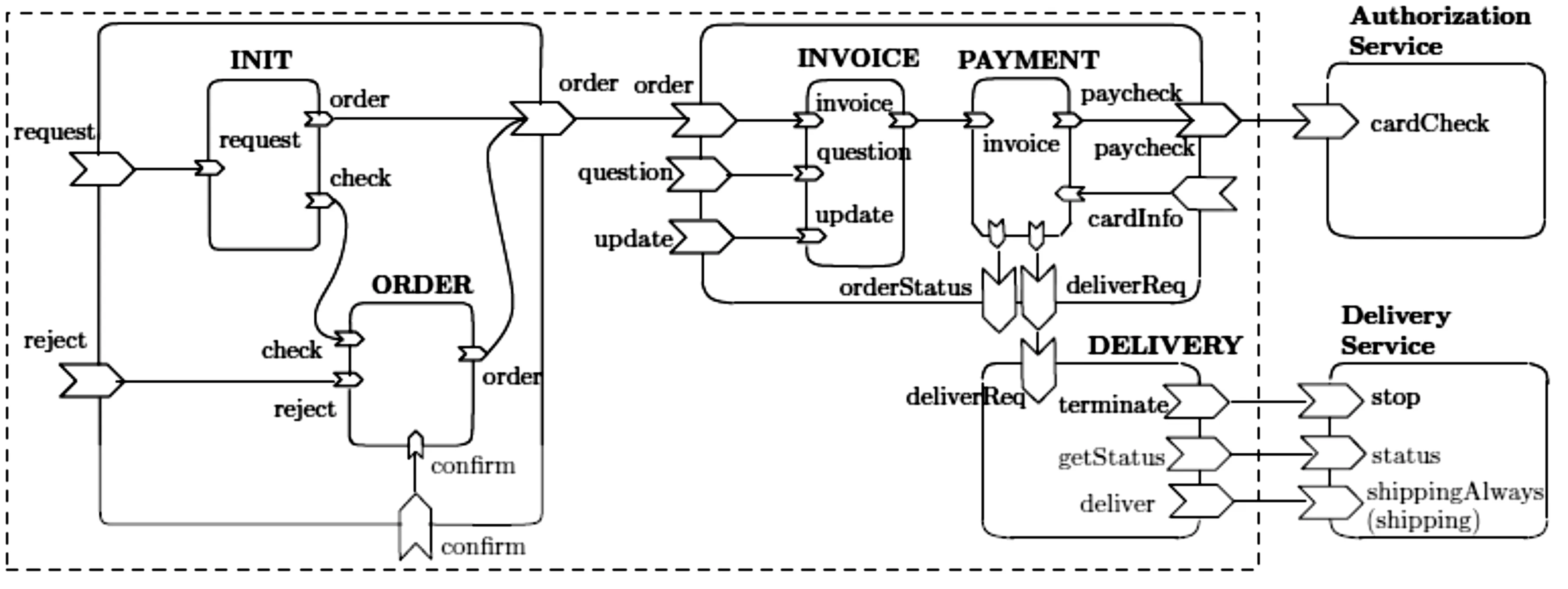
图3　在线购物系统的SCA

原子组件C11的端口定义为：

synchronous)，

required,synchronous)，

原子组件C12的端口定义为：

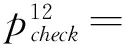
provided,synchronous)

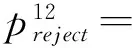
provided,synchronous)

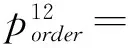
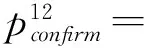
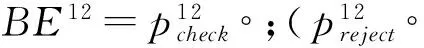
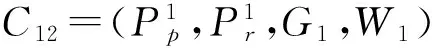
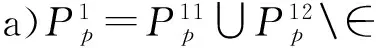
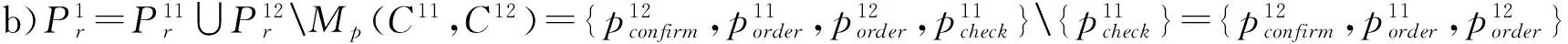
c)G1={}，

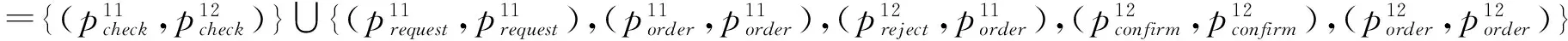
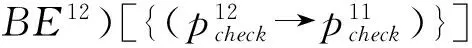
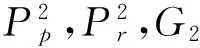
此外，假设运输服务提供者Cds提供的服务为：BEds=pshippingAlways◇◁b▷pshipping∘;pstatus∘;pstop◇；信用卡检查服务提供者Ccs提供的服务为：BEcs=pcardcheck∘。

令端口的关系集为：

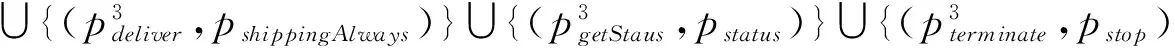
则在线购物系统的动态行为语义模型(记作SCAonline)为：

SCAonline=C1⊕C2⊕C3⊕Cds⊕Ccs.

其行为表达为：

BE=(BE1‖BE2‖BE3‖BEds‖BEcs)[Mw]

=BE1[Mw]‖BE2[Mw]‖BE3[Mw]‖

BEds[Mw]‖BEcs[Mw].

其次，根据测试可获得运行轨迹，于是有：

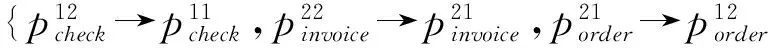
I=User-Inputs};

BE1=BE11‖BE12

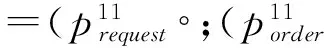
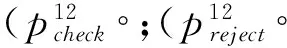
BE2=BE21‖BE22

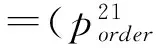
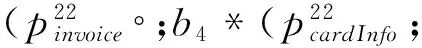
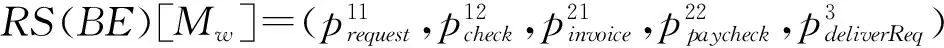
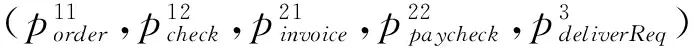
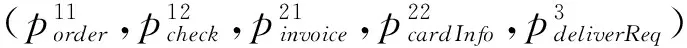
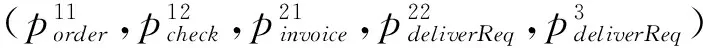
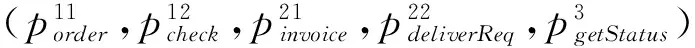
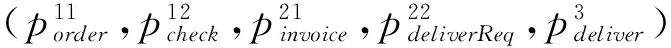
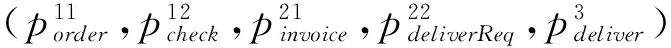
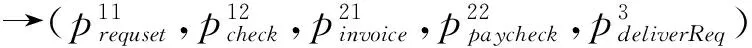
根据可达状态，可获得对应的Markob链模型，如图4所示。其中R1表示进入状态的可靠性，R15表示退出状态的可靠性，概率矩阵为：

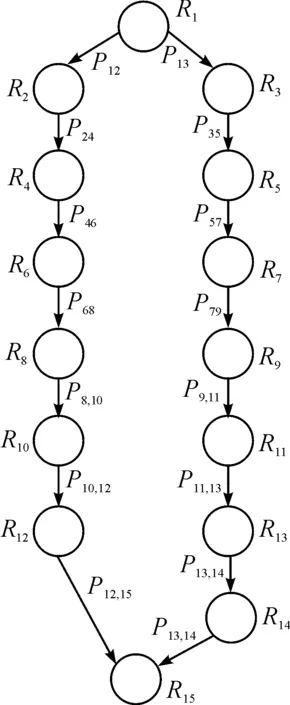
图4　在线购物系统对应的Markov链可靠性模型

因此，迁移矩阵为：

其中：R1=0.9812,R2=0.9943,R3=0.9932,R4=0.9961,R5=0.9903,R6=0.9973,R7=0.9906,R8=0.9983,R9=0.9953,R10=0.9975,R11=0.9946,R12=0.9952,R13=0.9934,R14=0.9878,R15=0.9978。

因此，根据可靠性计算公式有：T(1,15)=0.9484,R=T(1,15)*0.9978=0.9436。

6　结　语

本文提出了一种新的计算面向服务系统的可靠性方法。利用面向服务组件的架构，构建了Markov可靠性模型，它可在测试阶段重新配置。该方法的优点在于无需假设组件的失效是独立的。其次，考虑失效数据的获得，所提方法和已有方法是一个均衡过程。对于已有的基于组件的可靠性模型，因为失效数据来自组件，所以容易测试，但是无法反应内部的错误，因为对于一个输入，只有一个输出；对于本文提出的模型，失效数据来自端口，故能反应系统内部错误信息，但是需要增加额外的测试工作。

[1]CHENM,LYUMR,WONGWE.Effectofcodecoverageonsoftwarereliabilitymeasurement[J].IEEETransactionsonReliability, 2001, 50(2): 165-170.

[2]HAMLETD.Arewetestingfortruereliability[J].Software,IEEE, 1992, 9(4): 21-27.

[3]KRISHNAMURTHYS,MATHURAP.Ontheestimationofreliabilityofasoftwaresystemusingreliabilitiesofitscomponents[C]//SoftwareReliabilityEngineering, 1997.Proceedings,TheEighthInternationalSymposiumon.IEEE, 1997: 146-155.

[4]LITTLEWOODB.Softwarereliabilitymodeledformodularprogramstructure[J].IEEETransactionsonReliability, 1979, 28(3): 241-246.

[5]MAJ,CHENH.Areliabilityevaluationframeworkoncompositewebservice[C]//Service-OrientedSystemEngineering, 2008.SOSE′08.IEEEInternationalSymposiumon.IEEE, 2008: 123-128.

[6]DOLBECJ,SHEPARDT.Acomponentbasedsoftwarereliabilitymodel[C]//Proceedingsofthe1995conferenceoftheCentreforAdvancedStudiesonCollaborativeresearch.IBMPress, 1995:19-29.

[7]YACOUBS,CUKICB,AMMARHH.Ascenario-basedreliabilityanalysisapproachforcomponent-basedsoftware[J].IEEETransactionsonReliability, 2004, 53(4): 465-480.

[8]GOKHALESS,WONGWE,TrivediKS,etal.Ananalyticalapproachtoarchitecture-basedsoftwarereliabilityprediction[C]//ComputerPerformanceandDependabilitySymposium, 1998.IPDS′98.Proceedings.IEEEInternational.IEEE, 1998: 13-22.

[9]WANGW,PAND,CHENM.Architecture-basedsoftwarereliabilitymodeling[J].TheJournalofSystemandSoftware, 2006, 79(1): 132-146.

[10]CHEUNGRC.AUser-OrientedSoftwareReliabilityModel[J].IEEETransitionsonSoftwareEngineering, 1980, 6(2):118-125.

[11]GOSEVAPK,TRIVEDIKS.Architecture-basedapproachtoreliabilityassessmentofsoftwaresystems[J].PerformanceEvaluation, 2001, 45(2): 179-204.

[12]GOSEVAPK,MATHURAP,TrivediKS.Comparisonofarchitecture-basedsoftwarereliabilitymodels[C]//SoftwareReliabilityEngineering, 2001.ISSRE2001.Proceedings. 12thInternationalSymposiumon.IEEE, 2001: 22-31.

[13]CHAPMANM,EDWARDSM,BEISIEGELM,etal.Servicecomponentarchitectureassemblymodespecificationversion1.1[R].Technicalreport,OASIS, 2011.

[14]DINGZH,CHENZ,LIUJ.Arigorousmodelofservicecomponentarchitecture[J].ElectronicNotesinTheoreticalComputerScience, 2008, 207: 33-48.

(责任编辑： 陈和榜)

Architecture-based Prediciton of Service Combination Reliability

HUANGHongyuna,ZHANGJuanb,DINGZuohuaa

(a. School of Information Science and Technology; b.School of Science,Zhejiang Sci-Tech University, Hangzhou 310018, China)

Software reliability is an important index to measure the quality of software, while software architecture can help us to predict the software reliability. In order to study reliability of service combination based on Service Component Architecture (SCA), a new method is proposed, which needs not assume that component failures are independent. Markov model is built based on the execution of ports of SCA. Then, reliability of service combination is calculated in the combination of failure data of ports. The effectiveness of the method is demonstrated through the reliability calculation of an online shopping system.

service combination; architecture oriented to service component; port; reliability; failure data

10.3969/j.issn.1673-3851.2016.01.014

2015-02-27

国家自然科学基金项目(61210004，61170015)

黄鸿云(1977-)，女，江苏如皋人，硕士研究生，主要从事软件工程方面的研究。

丁佐华，E-mail：zouhuading@hotmail.com

TP311.5

A

1673- 3851 (2016) 01- 0084- 09 引用页码： 010602