大跨径钢管混凝土拱桥扣索索力计算方法综述
张 健,康胜清,邸庆辉
(重庆交通大学土木工程学院, 重庆 400074)
大跨径钢管混凝土拱桥扣索索力计算方法综述
张健,康胜清,邸庆辉
(重庆交通大学土木工程学院, 重庆 400074)
无支架缆索吊装与千斤顶斜拉扣挂相结合的施工方法已经成为大跨径钢管混凝土拱桥施工最常用的方法,其中扣索索力的确定已经成为施工中必不可少的一项重要控制参数。文章系统地综述了近年来扣索索力计算方法的研究现状,并进行了详细的阐述,总结了各个方法的优缺点,并根据钢管混凝土拱桥的施工特点,对钢管混凝土拱桥的施工方法作了进一步展望。
无支架;缆索吊装;千斤顶斜拉扣挂;大跨径;钢管混凝土拱桥;扣索索力
自从无支架缆索吊装千斤顶斜拉扣挂法在广西邕宁邕江大桥施工中得到成功运用后[1],该法已经成为目前大跨径钢管混凝土拱桥最常用的施工方法。在实现更加容易控制线形的同时,如何确定扣索的索力又成为了桥梁工作者亟待解决的问题。扣索索力的大小直接关系到拱肋节段标高以及所需扣索数目的确定,扣索索力的确定已经成为大跨度钢管混凝土拱桥中一项重要的控制参数。
目前方法主要有力矩平衡法[2],周水兴等人提出的零弯矩法[3-4],沈成武[5]等人提出零位移法,何雄君[6]、方建[7]、张治成[8]等人提出的索力优化分析法,蔡净[9]提出的定长扣索法,田仲初[14]提出的弹性-刚性支承法,陈得良、缪莉[15]提出改讲的弹性一刚性支承法。
1 力矩平衡法
力矩平衡法[1]是指在该钢管混凝土拱桥施工过程中,假设每段钢骨架刚度相对于扣索刚度为极大值,各段钢骨架之间的联接考虑为铰接,各段钢骨架结构重量力为自重加上施工荷载。吊装拱顶时,作用在最大悬臂段端头的作用力考虑为25 %~50 %的重量。
力矩平衡法的优点是可以通过手算求解,各个工况下的扣索索力值可以有节点力平衡的原理推导出通用计算公式,不受架设节段的限制,计算方法简单明了,但是也存在明显的缺点:
(1)计算假设吊装的拱肋是直杆,但是现实中的拱肋是曲杆,同时需要计算拱肋的重心。
(2)计算只适用于各节段临时铰接的情况,不能用于节段接头固结的情况。
(3)计算假定拱脚为铰接,对于拱脚固结的情况无法适用。
(4)需要频繁调整索力,使拱肋线形符合设计线形不利于施工的简化。
力矩平衡法和实际施工存在一定的差异:邕宁邕江大桥采用的合龙方式为先松部分扣点然后合龙,而现在通常是合龙之后再松扣索,合龙后整拱承受合龙段的重量而不是最大悬臂端头承受合龙段部分重量。
2 零位移法
零位移法是指在索力计算过程中以考虑预拱度后的设计拱轴线作为调索的标准线形,将扣索扣点直接简化成支座,约束扣点位移[10],即各扣点位移考虑为0,支座反力为0。扣索索力或扣索索力的增量即为各扣点X与Y方向反力的合成。在整个施工过程中各扣点受约束位移始终保持为0,所以称为“零位移法”。零位移法计算示意图见图1、图2。

图1 零位移法计算扣索索力有限元模型
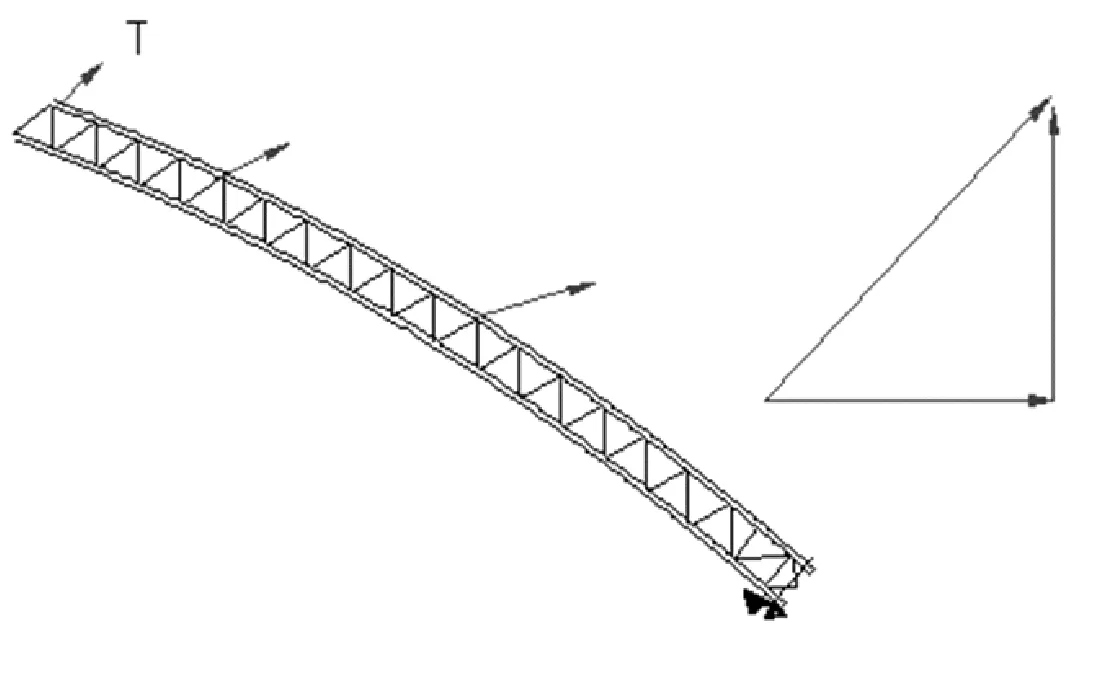
图2 扣索索力合成模式
零位移法计算原理简单明了,力学概念清晰,每节段不需要设置预抬高值,可以适用于节段之间的各种联接方式。但是每吊装一个节段,都需要对每根扣索索力以及控制标高进行调整,在实际的工程应用中十分繁琐,对施工过程的简化不利。
3 零弯矩法[3-4]、[11]
零弯矩法是在力矩平衡法的基础上由周水兴教授提出,零弯矩法的成立条件为:
(1)无论各节段之间是临时铰接还是固结(焊接)都要保证拱肋各阶段接头处的弯矩为零,即节段接头零弯矩。
(2)保证拱脚处不产生附加弯矩,确保吊装合龙时拱脚不会产生弯矩应力,即拱脚零弯矩。
在拱肋吊装施工过程中,通过张拉扣索,不断地调整扣索索力,确保各节段接头处弯矩为0,使其满足零弯矩法成立的条件。从而可以解决吊装过程中拱脚为固结的情况下扣索索力计算的问题。
具体计算公式推导可参考文献[17]。零弯矩法克服了力矩平衡法的不足之处,通过积分的方式计算力矩,不需要计算节段的重心,无论节段式临时铰接还是固结均可计算,扣索索力的计算在任意施工阶段均可进行。虽然零弯矩法计算出的扣索索力比较精确,但是需要在施工过程中不断地调整索力,对于吊装节段较多的工况,需要进行繁琐的调索工作。在应用“零弯矩法”计算扣索索力时也存在一定的问题[12],主要是一些实际工程中斜拉扣挂系统的扣塔位置、塔高和拱肋上扣点的位置等决定了应用“零弯矩法”计算出的扣索索力出现负值和不均衡(即各根扣索索力相差较大)的情况。因此,“零弯矩法”有一定的适用范围。对一些特定的实际工程,用“零弯矩法”计算扣索索力是行不通的,要采取一定的措施或应用其他索力计算方法计算扣索索力。
4 定长扣索法[13]
定长扣索法是指根据倒装分析法确定每一根扣索的放样长度,依靠扣索自身的弹性伸长使拱肋达到设计轴线位置。定长扣索法在浙江省三门市健跳大桥[4]的主拱肋吊装施工中得到成功应用。其突出优点是扣索索力比较均匀,扣索只需要一次张拉即可,所以称为定长扣索法。
在拱肋节段吊装施工中,节段标高要高于设计轴线,待拱肋各节段达到设计轴线后焊死固结,扣索刚度相对于钢管截面刚度来讲很小,所以视拱肋节段为刚体,即在拱肋吊装施工中认为拱肋节段只有刚体位移,忽略拱肋节段本身的弹性变形。拱肋节段刚体的位移由扣索的弹性变形、索塔的位移、拱肋节段在主索、扣索、缆风索等索力作用下的变形组成。定长扣索法的基本思想是:已知上一节段的标高,通过几何关系可以唯一确定下一节段标高。从而可以根据平面杆系程序或空间杆系程序进行仿真计算,计算各扣索索力以及节段的预抬高值。具体计算公式推导可参考文献[18]。
5 优化分析法
优化分析法是指在计算扣索索力过程中,在考虑拱肋线形和内力的同时,将最优化分析理论引入拱肋计算索力过程中,从而求解最优索力。
优化分析计算中,评价标准称为目标函数,以变量形式参与结构优化分析的称为设计变量,设计中应遵守的几何、强度及刚度等条件称为约束条件。扣索索力优化法的基础是零位移法,忽略扣索对拱肋节点的约束作用,用索单元模拟扣索参与整体结构的分析,经过非线性迭代计算,根据最优函数计算出一组最优索力值,将计算结果进行正装和倒装计算,判定其能否满足拱肋骨架的正装和倒装要求。当计算结果能够同时满足施工过程中的安全、稳定、强度要求后,根据计算结果给出一组标高、索力控制数据,指导施工。
张克波、王国俊根据影响矩阵的概念[16],确定张拉变量子序列{x1,x2,x3..........xn},并据此建立影响矩阵,并将最优化的计算理论引入到拱肋悬拼中的扣索索力计算中。在对结构进行空间有限元分析的基础上,以拱肋各标高控制点高程偏差的平方和最小为优化目标,以扣索索力作为设计变量,通过约束扣索的最大索力值、单个控制点的标高偏差及内力控制截面的最大Mises应力值,迭代优化出最佳索力[17]。
6 弹性一刚性支承法
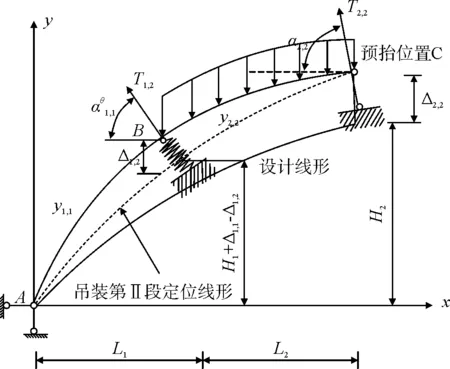
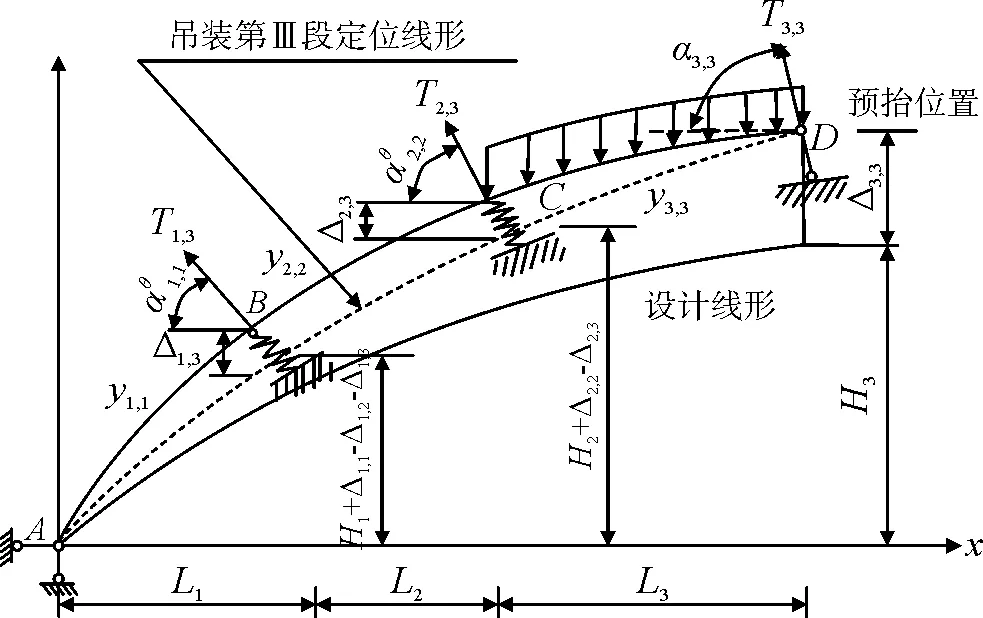
田仲初[14]提出连续体弹性-刚性支承法,能同时计算扣索索力与确定拱圈的预抬高值。连续体弹性-刚性支承法的主要思想是将当前吊装施工节段的扣索用刚性支承来模拟,将已吊装节段的扣索用弹性支承来模拟,相邻节段之间的联接作为弹性体来考虑,该方法能够同时求得扣索索力和标高预抬量。
陈得良、缪莉[15]在田仲初提出的弹性-刚性支承法基础上提出改进的弹性-刚性支承法,具体思想是将当前施工节段的扣索模拟为刚性支承,己吊装阶段的扣索模拟弹性拉索,相邻节段之间的联接作为转动弹簧来考虑,转动刚度为0 图3 第Ⅰ节段安装示意 图4 第Ⅱ节段安装示意 图5 第Ⅲ节段安装示意 图6 合龙段安装示意 上面所述方法均有各自的局限性,也有各自的优点,可以看出,单一的扣索索力计算方法还不足以使控制结果达到满意的程度。可以根据钢管混凝土结构的特点,有针对性地选择几种计算方法,建立能将各方法的计算结果融合起来的计算模块,再集成于仿真测试系统中。这也使计算结果更贴近实际的一条重要途径。同时也可以将永久模板应用于钢管混凝土拱桥的外包工况中。 [1]郑皆连, 徐风云, 唐柏石, 等. 广西邕宁邕江大桥千斤顶斜拉扣挂悬拼架设钢骨拱桁架施工仿真计算方法[C]//中国公路学会桥梁和结构工程学会1996 年桥梁学术论文集. 北京: 人民交通出版社, 1996. [2]范立础. 桥梁工程(下册)[M]. 北京: 人民交通出版社,1985. [3]周水兴, 江礼忠, 曾忠, 等. 拱桥节段施工斜拉扣挂索力仿真计算研究[J]. 重庆交通学院学报, 2000,19(3): 8-12. [4]周水兴.浙江三门健跳大桥拱肋安装与施工控制计算[J].重庆交通学院学报, 2002, 21(2): 2-5. [5]沈成武,杜国东,何雄君,等.大跨度钢管砼吊装过程力的逆分析[J].武汉交通科技大学学报, 1998, 22(3): 223-226. [6]何雄君,沈成武,陈巧生,等.钢管混凝土拱桥主拱钢管缆索吊装扣索索力调整 [J]. 武汉交通科技大学学报, 1999, 23(5): 575-578. [7]方建,王箭明,陈晓辉.青干河大桥主拱空管吊装过程的索力逆分析和优化 [J].钢结构, 2003,18(6):40-42. [8]张治成,叶贵如,陈衡治.大跨度钢管砼拱桥拱肋吊装中的扣索索力计算[J].浙江大学学报,2004,38(5):610-614. [9]蔡净.定长扣索法安装拱桁架节段控制索力计算[J].中南公路工程, 2003, 28(3): 16-18. [10]周汉东,许晓锋,黄福伟.大跨径钢管混凝土拱桥钢管拱肋吊装施工控制[J].哈尔滨建筑大学学报,1997(增刊). [11]郑春玲,雷霆.某钢管拱桥拱肋悬拼中的扣索计算[J].桥梁建设,2001 (4): 35-37. [12]张玉平,李传习,董创文.“零弯矩法”应用于斜拉扣挂索力确定的讨论[J].交通与工程, 2004, 20(1): 15-18. [13]周水兴,蔡净,熊洪滨.定长扣索法安装拱析架节段控制索力计算[J].工程力学,2001(增刊):838-842. [14]田仲初,陈得良,颜东煌,等.大跨度拱桥拱圈拼装过程中扣索索力和标高预抬量的确定[J].铁道学报, 2004, 26(3): 81-87. [15]陈得良,缪莉,田仲初,等.大跨度桥梁拱肋悬拼时扣索索力和预抬量计算[J].工程力学,2007, 24(5): 132-137. [16]张克波,王国俊.大跨度钢管混凝土拱桥拱肋吊装中的扣索索力计算[J].长沙理工大学学报:自然科学版,2005,2(4): 17-21. [17]陈妍如. 大宁河特大桥拱肋安装斜拉扣索索力与预抬量计算分析[D].重庆交通大学,2008. [18]柳江涛. 缆索吊装钢管混凝土拱桥拱肋的线性问题研究[D].北京交通大学,2011. 张健(1990~), 男,硕士,研究方向为桥梁与隧道工程。 U445.464 B [定稿日期]2016-04-29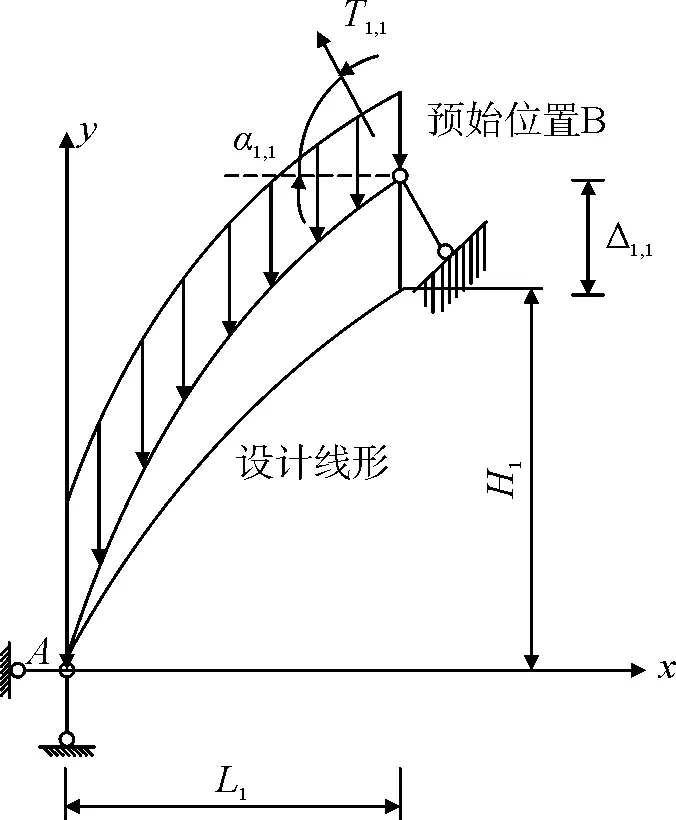

7 展望

