一种阵列天线快速波束赋形方法

王　力，何丙发，孙庆锋

(南京电子技术研究所，　南京 210039)



·天馈伺系统·

一种阵列天线快速波束赋形方法

王力，何丙发，孙庆锋

(南京电子技术研究所，南京 210039)

介绍了一种阵列天线快速赋形方法，该方法基于Orchard综合，采用遗传算法对Schelkunoff单位圆零点的位置移动实现波束赋形。波束赋形分为两个步骤：1)根据副瓣电平采用解析法确定初始零点位置；2)以赋形区域内零点径向位移作为自由度，用遗传算法进行赋形区域单目标寻优。相对常见以阵元的幅度相位作为自由度编码的遗传算法赋形，该方法不仅有效避免了副瓣和赋形区的多目标均衡问题，而且算法自由度大幅减少，收敛速度快，能够同时实现较低副瓣电平和赋形区精度要求。通过余割平方赋形和扇形波束两个实例说明该方法的有效性，可以应用于阵列天线快速赋形设计。

波束赋形；Orchard综合；遗传算法

0　引　言

在雷达、通信等领域中，往往需要特殊形状的天线波束赋形。根据波束形状求解阵列天线单元间距、激励的幅度和相位称为天线综合。这是天线设计过程中一个非常重要的环节。

实现波束赋形常见方法为解析法和各类搜素算法。解析法包括傅里叶变换法和Woodward综合法等[1]。傅里叶变换法是综合方向图最直接的方法，但是这种方法需要获得目标方向图的解析表达式，求解困难。Woodward综合法也被称作零点填充法，在赋形区域能较好逼近预期方向图，但在非赋形区域却不能控制副瓣电平。

除了解析法，各类搜索算法也逐渐被天线设计所采用。Powell算法[2]等直接搜索算法思路简单、计算速度快，然而属于局部寻优算法，寻优能力受限。除此以外，智能搜索算法由于其全局搜索特性得到广泛应用，典型的搜索算法包括遗传算法[3]和粒子群算法[4]以及基于上述算法的改进[5-6]。

遗传算法是20世纪60、70年代由Holland等人提出的一种全局优化算法，通过模拟生物进化过程寻找最优解，本质上是一种高度并行、随机、自适应全局搜索方法。遗传算法简单通用、稳健性强，适用于处理传统搜索方法难于解决的复杂和非线性问题，近年来，在天线阵列的设计中有较多应用。

采用遗传算法实现天线波束赋形时，通常采用所有阵元的激励幅度和相位作为自由度进行编码，方向图中赋形与副瓣等区域需要分别满足误差与副瓣电平等多个目标。因此，存在如下问题：(1)变量自由度为阵元数目的2倍，当阵元数目较多时，计算速度明显减慢；(2)多目标优化容易陷入局部收敛，造成单目标占优；(3)低副瓣难以控制，当副瓣低于-30dB时，实际副瓣电平小于主瓣电平的1/1 000，阵元的幅相微小扰动就会造成副瓣较大起伏，因此副瓣进一步降低的程度有限。

为了解决上述问题，本文提出了一种新的零点优化算法。该方法基于Schelkunoff单位圆零点以及Or-chard综合[7]，以满足副瓣要求零点分布作为初始值，赋形区域内的零点沿单位圆径向位置变化作为自由度，采用遗传算法进行赋形优化。本方法有如下优势：副瓣目标由初始值实现，自由度显著减少，多目标函数简化为仅仅赋形区域单目标函数，求解空间缩小，收敛速度加快，赋形精度明显提高，可广泛应用于各类赋形天线设计中。

1　优化方法

1.1Schelkunoff单位圆

Schelkunoff方法是天线阵列方向图综合中的一种经典方法，可以在方向图的指定位置产生零深。相比于其他综合方法，这是一种更深入实质的波束方向图综合技术。

由N个阵元均匀分布构成的一维天线阵列阵因子可以写成

(1)

式中：In为第n个阵元的电流激励系数，具有复数形式；k=2π/λ为波束。在式中作变换u=sinθ，z=exp(jkdsinθ)，于是，阵列多项式可以写为

(2)

以上多项式有N-1个复数根，通过因式分解得到

(3)

不妨令IN=1，并不影响方向图特性，因此阵列因子的幅值可以简化为

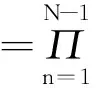
(4)

式中：zn=exp(jkdsinθn)，限制在单元圆上的复平面上的点，决定了方向图中零点的位置。阵列因子的幅度等于单位圆上的点z=x+jy与各零点zn直线线段长度的乘积，如图1a)所示。通过控制单位圆上的零点位置，增加主瓣宽度，降低副瓣电平。

Orchard等人提出了一种新的方向图综合技术，增加了零点位置的自由度，由单位圆扩展到了单元外(内)，零点还可以沿单位圆径向自由移动，自由度由θn增加为(θπ, rn)，此时，zn=rnexp(jkdsinθn)，将式(4)展开后求得系数即为阵元的电流激励。Orchard零点控制的优势在于能够灵活控制每个起伏电平或者副瓣电平。

图1b)为将副瓣区域内任意两个零点移至单位圆外后的方向图。从图中可以看出，增加零点自由度后，不仅可以改变副瓣电平，而且可以任意改变主瓣或者副瓣的形状，由此方向图可以分为赋形区和副瓣区两个部分：副瓣区域N1个零点被限制在单位圆上，赋形区域N2个零点自由移动，方向图由N1+2N2个变量决定，通过各类算法即可求得最优方向图和零点位置，最终将多项式展开得到每个阵元的幅相分布。

图1　单位圆零点位置及方向图综合

1.2遗传算法

遗传算法中包含了如下四个基本要素，如图2所示。

图2　遗传算法流程

1)编码：通过编码将各种解表示成遗传空间可以直接进行算子操作的基因型串结构数据。方向图综合问题中包括每个阵元的电流幅度和相位两个变量，通常采用级联方式进行编码。若N个阵元的天线阵列第k个天线单元激励电流的幅度和相位分别为Ik和φk，采用级联编码后，每组数据结构可以表示成(I1,I2,…,IN, φ1,φ2,…,φN)的形式。

2)初始群体：为遗传操作准备的由若干初始解组成的初始群体。

3)适应度函数：遗传算法在搜索进化过程中用适应度函数值来评估个体或解的优劣，并作为以后遗传操作的依据，通常取函数最大值或者最小值。

方向图赋形综合是一个多目标多参数的非线性优化问题，除了在赋形区需要逼近目标方向图外，在非赋形区还要尽可能地抑制副瓣电平。因此，适应度函数要包括这两个子目标函数。通常采用权系数法，把这两个子目标函数按一定的权值相加，使之转变成单目标优化问题。

设目标方向图为F0(θ)，综合后实际方向图为F(θ)，允许的最大误差电平为eth；目标最大副瓣电平为SLL0，实际最大副瓣电平为SLL；上述赋形主瓣与副瓣区域的目标函数可以分别表达成

(5)

(6)

对两个子目标赋予不同的权重w1和w2，则适应度函数可以写成

(7)

通过计算适应度函数的最小值，即可求得最优化方向图。

4)遗传操作设计，包括选择、交叉和变异：

(1) 选择：从群体中选择优胜个体，把优化的解直接遗传到下一代。个体适应度越高，其被选择的机会就越多。

(2) 交叉：把两个父代个体的部分结构互相交换重组，生成新的个体。

(3) 变异：对群体中的个体串的某些位置上的基因值作变动。

在实际方向图综合中发现，如果以阵元电流幅度和相位作为自由度，采用遗传算法直接求解存在如下三个问题：

1) 自由度较多，每个阵元都包含幅度和相位两个自由度，全阵列共有2N个自由度，随着阵元的增加，计算量将急剧增加，收敛速度明显变慢；

2) 需要同时兼顾赋形区域与副瓣区域两个目标，很难选择合适的权系数w1和w2来平衡这两个优化目标，容易使某一种模式占优，导致另外一个优化目标难以实现，优化效果有限；

3) 初始值不确定，搜索范围较大，容易陷入局部最优。

1.3优化零点算法

为了解决以上问题，结合Orchard综合灵活直观的优点，本文提出了基于Schelkunoff单位圆以及Orchard综合的遗传算法波束赋形，如图3所示。由于阵元的电流幅相分布与方向图零点位置存在对应关系，因此可以将求解电流幅相Ik，φk分布等价为求解零点位置θk，rk。通过详细分析赋形区域和副瓣区域零点位置变化对方向图的影响，还可以发现：

(1)赋形区域内零点位置的变化对副瓣区域电平的影响较小(第一副瓣零点除外)，因此，副瓣优化可以在各种优化算法前直接由解析方法计算完成；

(2)常见赋形如余割赋形等可以由仅仅移动赋形区域内零点径向位置rR来实现，因此，自由度由Orchard综合的N1+2N2个进一步减少为N2个。

基于上述特点，本文提出的优化零点算法流程分为两个步骤：求解初值和赋形优化。首先，根据副瓣电平，通过解析法求得所有零点位置，将前述零点位置作为初始值；然后，将赋形区域零点径向位置rk作为变量，通过遗传算法求得最优解下的零点位置；最后，根据式(4)展开求得阵元幅相分布。

图3　优化算法流程

相比于直接求阵元幅相分布的算法，本方法有如下两个优势：

1)副瓣约束已经由初始值通过解析法确定，适应度函数简化为赋形区域的单目标函数，避免了多目标下权重的难以分配和单目标占优的问题；

2)对零点的移动方向加以限制，仅仅允许赋形区域内的零点沿径向移动，算法自由度大幅减少，计算速度加快。同时，避免了二维空间搜索易陷入局部最优的问题。

2　计算实例

2.1程序实现

为了进一步减少与期望值之间的误差，提高计算效率，本文还改进了一种界面化操作方案，可以自由移动零点位置，并实时显示对应的方向图。程序采用MATLAB的GUI工具编写，界面同时显示零点位置、对应方向图、幅相分布以及赋形各项参数设置，如图4所示。通过直接选中并移动赋形区域内的零点位置，将方向图尽可能逼近期望值曲线。将此时的零点位置作为计算初始值，赋形区域内零点的rk作为自由度进行优化计算，进一步缩小搜索范围，提高算法的收敛速度。应用遗传算法，可以快速求得最优化的赋形。遗传算法主要采用了MATLAB自带优化算法工具箱中的GA函数来实现。

图4　程序界面

2.2算法实例

2.2.1余割赋形

20个等间距排布的线阵，单元间距0.5个波长。优化每个阵元的幅度和相位，使阵列的主瓣方向满足余割平方赋形，其余空间区域副瓣电平SLL小于-25dB。目标函数可以写为

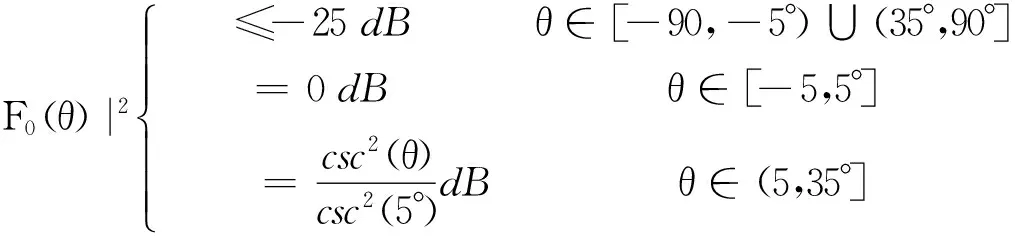
(8)

根据本文优化算法，首先计算副瓣区域零点分布。根据副瓣目标，不妨令线阵满足SLL=-25dBTaylor分布，方向图零点位置满足解析表达式

(9)

以上述解析求得的零点位置作为初值，通过遗传算法优化赋形区域内的五个零点径向位置rk，以赋形区域内与期望值的误差均值作为遗传算法的适应度函数，此时，目标函数为单目标函数

(10)

经过300次迭代计算，优化后的方向图以及幅相分布如图5所示。作为对比，该赋形算例还采用了直接以每个阵元的Ik和φk作为自由度的遗传算法，适应度函数采用加权系数法，如式(7)所示。同样经300次计算后的方向图和幅相分布如图5、图6所示。从图中可以看出，采用本文方法优化后的方向图不仅在赋形区域与期望值误差非常小，而且副瓣完全满足甚至优于设计要求。而采用直接幅相优化由于需要同时兼顾赋形区域和副瓣电平，优化效果十分有限。

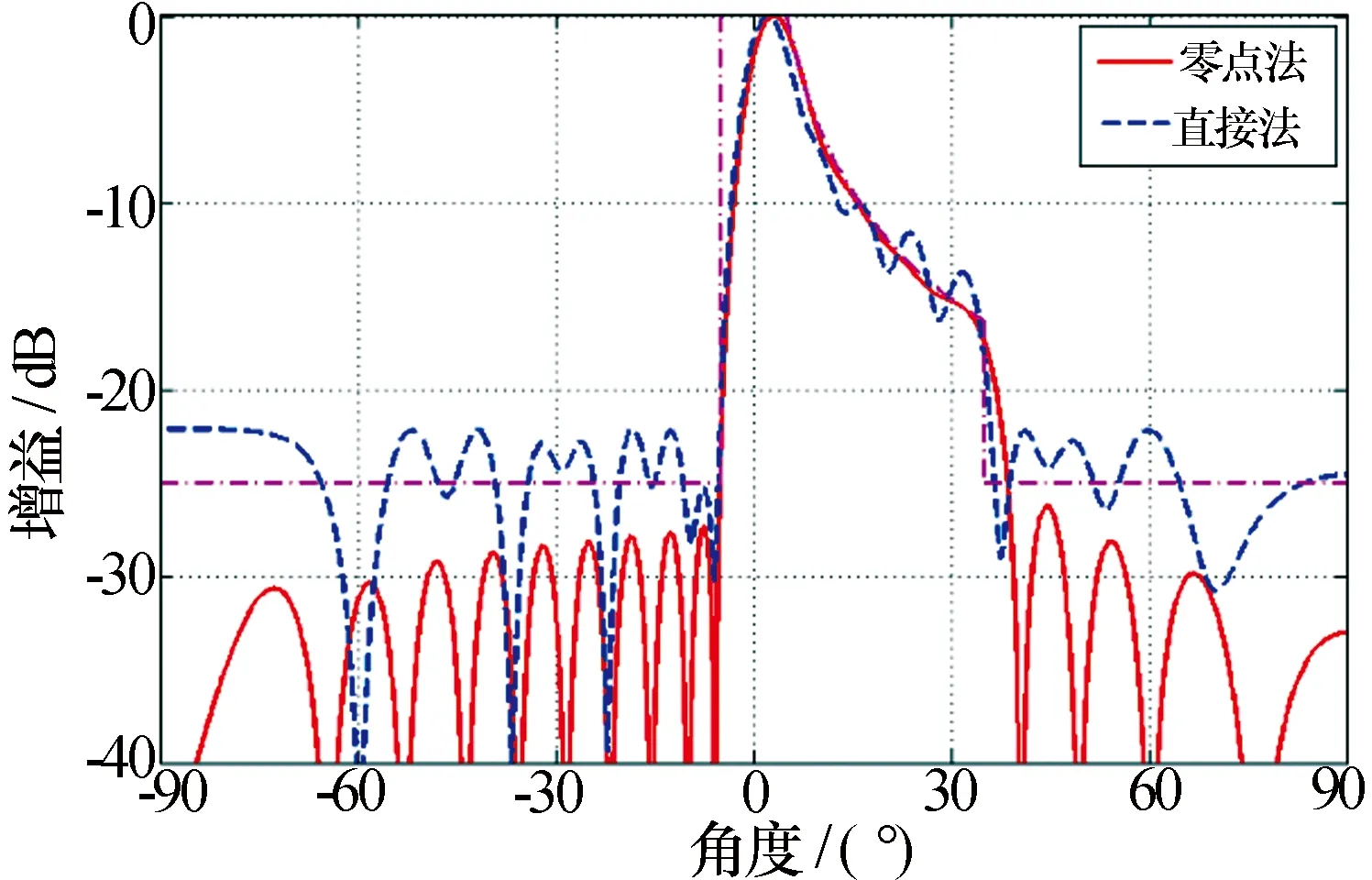
图5　优化零点算法与直接幅相算法方向图

图6　两种算法每个阵元激励幅相分布比较

2.2.2扇形波束

同样为20个等间距排布的线阵，单元间距0.5个波长。目标函数(见图7中点划线)可以写为

(11)

同样采用算例1中的直接幅相遗传算法和本文所述优化零点算法分别进行计算，方向图和阵元的幅相分布如图7和图8所示。从图7中可以看出，采用优化零点算法中赋形区域内的幅度起伏小于0.5dB，赋形区域外的副瓣小于-30dB，波束特性明显优于直接幅相遗传算法。

图7　优化零点算法与直接幅相算法方向图

图8　两种算法每个阵元激励幅相分布比较

需要说明的是，由于方向图采用dB单位表示，而采用单位1表示时，实际的副瓣电平非常小，在0附近波动，当副瓣要求<-25dB以下时，阵元幅相的微小扰动都会对副瓣造成较大起伏，这也是采用直接计算幅相的遗传算法时副瓣很难进一步降低的原因之一。同时，多目标优化也容易导致单目标占优。图9为零点法和直接法的收敛速度比较，由于两种算法的适应度函数不一致，将二者的最终收敛值进行归一化后在图9中显示。从图中可以看出，优化零点算法的收敛速度相比直接算法有了显著提高。

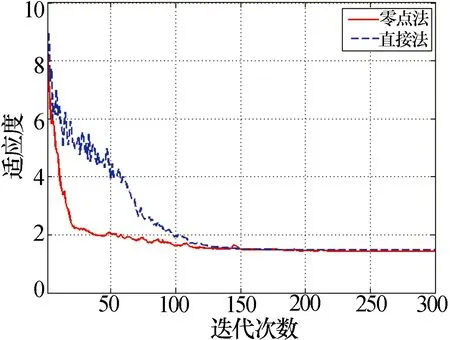
图9　两种算法收敛速度比较

3　结束语

本文提出了一种基于Schelkunoff单位圆以及Orchard综合的优化零点算法，先通过解析方法计算零点位置，满足副瓣约束，将求得的零点位置作为初始值，赋形区域内的零点径向位置变化作为自由度，进行区域内单目标遗传算法寻优。不仅避免了直接幅相计算中多目标均衡问题，也显著减少了自由度，加快收敛速度。通过低副瓣平方余割波束和扇形波束两个实例可以看出，副瓣区域和赋形区域均得到了优化，明显优于直接幅相计算法所得的结果，说明这种算法具有很好的应用价值。

[1]MAILLOUXRJ.Phasearrayantennahandbook[M]. 2nded.Beijing：PublishingHouseofElectronicsIndustry, 2007.

[2]MARTINSCL,PATENUDEY,SEGUING.Lineararraybeamshapingusingfletcher-powelloptimization[C]//Antennas&PropagationSocietyInternationalSymposium.Philadelphia,PA:IEEEPress, 1986: 395-398.

[3]刘昊, 郑明, 樊德森, 等. 遗传算法在阵列天线赋形波束综合中的应用[J]. 电波科学学报, 2002,17(5): 539-542.

LIUHao,ZHENGMing,FANDesen,etal.Synthesisofantennaarraysshaped-beamusinggeneticalgorithm[J].ChineseJournalofRadioScience, 2002, 17(5): 539-542.

[4]杨丽娜, 丁君, 郭陈江,等. 基于遗传算法的阵列天线方向图综合技术[J]. 微波学报, 2005, 21(2): 38-41.

YANGLina,DINGJun,GUOChenjiang,etal.Patternsynthesisofantennaarrayusinggeneticalgorithm[J].JournalofMicrowaves, 2005, 21(2): 38-41.

[5]刘燕, 郭陈江, 丁君, 等. 基于粒子群算法的阵列天线波束赋形[J]. 电子测量技术, 2007, 30(6): 43-45.

LIUYan,GUOChenjiang,DINGJun,etal.PatternsynthesisofarrayantennabasedonPSO[J].ElectronicMeasurementTechnology, 2007, 30(6): 43-45.

[6]李绪平, 赵交成, 段霞霞, 等. 一种综合赋形波束天线阵的组合算法[J]. 微波学报, 2007, 23(6): 26-28.LIXuping,ZHAOJiaocheng,DUANXiaxia,etal.Synthesisoftheshaped-beamarrayantennasusinganewcombinedalgorithm[J].JournalofMicrowaves, 2007,23(6): 26-28.

[7]杨永建, 王晟达, 马健, 等. 基于改进粒子群算法的共形阵列天线综合[J]. 现代雷达, 2012, 34(12): 64-67.

YANGYongjian,WANGShengda,MAJian,etal.Conformalantennaarraybeampatternsynthesisbasedonimprovedparticleswarmoptimization[J].ModernRadar, 2012, 34(12): 64-67.

[8]ORCHARDHJ,ELLIOTRS,STERNGJ.Optimizingthesynthesisofshapedantennapatterns[J].MicrowaveAntennas&PropagationIEEEProceedingsH, 1985, 132(1): 63-68.

王力男，1986年生，工程师。研究方为相控阵天线技术等。

何丙发男，1963年生，研究员级高级工程师。 研究方向为相控阵天线技术、通信天线技术等。

孙庆锋男，1978年生，高级工程师。研究方为相控阵天线技术、毫米波天线技术等。

Synthesis of the Shaped-beam Array Antennas Using a Fast Algorithm

WANG Li，HE Bingfa，SUN Qingfeng

(Nanjing Research Institute of Electronics Technology,Nanjing 210039, China)

Afastalgorithmforsynthesisoftheshaped-beamarrayantennasispresented.ThisalgorithmisrealizedbymovingthezeropointpositionsontheSchelkunoff'sunitcircleusinggeneticalgorithm,basedontheOrchardsynthesis.Theprocedureisdividedintotwosteps: 1)analyticallycalculatetheoriginalzeropointpositionsaccordingtothesidelobelevel; 2)thefreedomofzeropointmovementintheshapingareaisrestrictedintheradicaldirection,andfindthebestresultwithsingle-targetbygeneticalgorithm.Comparedtothenormalantennashapingusingamplitude-phasecodinginthegeneticalgorithm,thismethodcanavoidthemulti-objectivetrade-offbetweenthesidelobelevelandbeamshapingaccuracyefficiently,andthefreedomofvariableforthealgorithmisreduced,theconvergencevelocityisalsoenhanceddramatically.Besides,lowsidelobelevelandbeamshapingwithhighprecisioncanberealizedsimultaneously.Theefficiencyforthisalgorithmisverifiedbyshapedsquare-cosecandfanbeamsample,anditcanfindwideapplicationsintheareaoffastbeamshapingforthearrayantennas.

shaped-beam；Orchardsynthesis；geneticalgorithm

10.16592/j.cnki.1004-7859.2016.08.016

王力Email：wangli860420@163.com

2016-04-26

2016-07-02

TN821+.8

A

1004-7859(2016)08-0070-05