β级α型Bazileviˇc函数的对数系数

牛潇萌，李书海

（赤峰学院数学与统计学院，内蒙古 赤峰　024000）

β级α型Bazileviˇc函数的对数系数

牛潇萌，李书海

（赤峰学院数学与统计学院，内蒙古 赤峰024000）

利用从属关系给出|(g(z)/f(z))α|的估计.运用构造一个非负函数和对复变函数模的积分进行估计的方法，对β级α型Bazileviˇc函数类Bα(β)的对数系数bn进行研究.所得结果推广了一些作者的相关结果.

单叶函数；对数系数；Bazileviˇc函数

1　引言

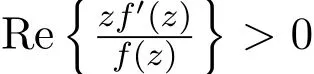
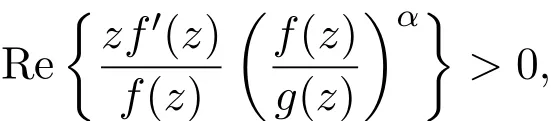
设 f(z)与 g(z)在 U内解析，如果存在 U内满足 |ω(z)|≤|z|的解析函数 ω(z)，使得g(z)=f(ω(z))，则称g(z)从属于f(z)，记作g(z)≺f(z).

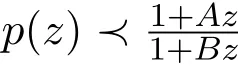
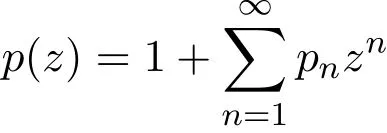
设α＞0，β∈R，f(z)∈S，如果存在g(z)∈S∗，使得则称f(z)∈B(α，β)[3].

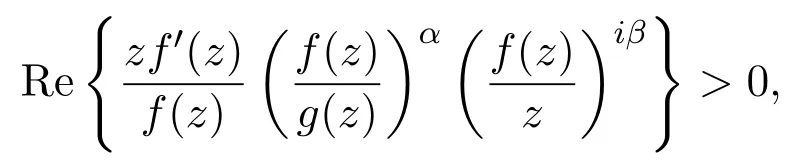
文献［4］给出了如下α型β级Bazileviˇc函数类Bα(β).

定义 1.1设f(z)∈S，α≥0，0≤β＜1，若存在g(z)∈S∗，使得

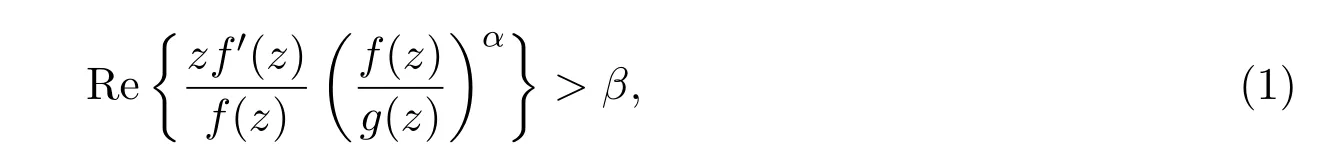
则称f(z)∈Bα(β)，其中的幂函数取主值.显然Bα(0)=Bα.设f(z)∈S，若则称bn为f(z)的对数系数.对数系数的估计在单叶函数的系数估计中有重要作用.Keobe函数k(z)=z(1-z)-2的对数系数为bn=1/n.对bn(n≥2)的估计，现在已经证明：

(1)当f(z)∈S∗时，|bn|≤[5]；(2)当f(z)∈C时，|bn|≤A，其中A表示一个绝对常数[6]；(3)当f(z)∈Bα时，|bn|≤A(1+α)，其中A表示一个绝对常数[7]；(4)当f(z)∈Y时，|bn|≤A，其中A表示一个绝对常数[8]；(5)当f(z)∈B(α，β)时，|bn|≤A，其中A表示一个绝对常数[9].

本文研究Bα(β)的对数系数.

2　引理

引理 2.1[9]设f(z)∈S，则

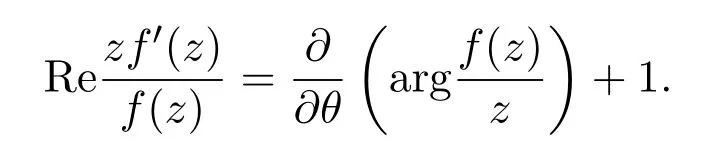
引理 2.2[9]设f(z)∈S，α∈C.则，z=reiθ，0＜r＜1，

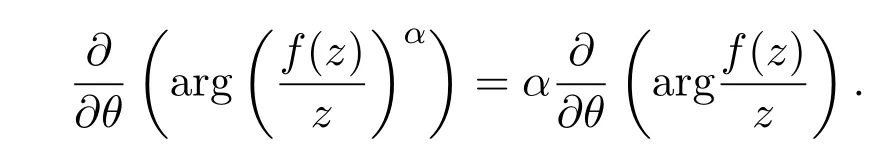
引理 2.3[6]设f(z)∈S，则对z=reiθ，≤r＜1，有(1)

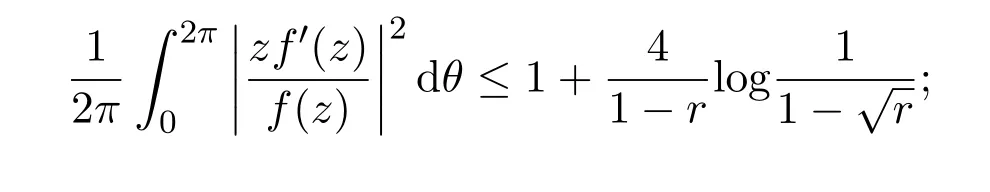
(2)

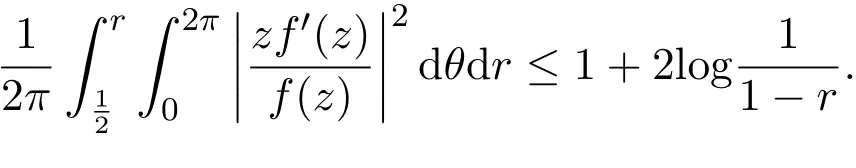
引理 2.4[10]设g(z)∈S∗，则arg g(z)＞0且引理 2.5[11]设f(z)∈S，则对0＜r＜1，有

引理 2.6设f(z)∈Bα(β)，g(z)∈S∗使得(1)式.则对z=reiθ，0≤r＜1，有

(1)

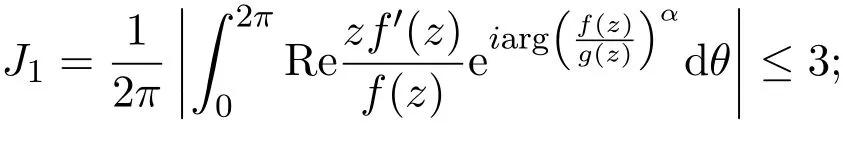
(2)

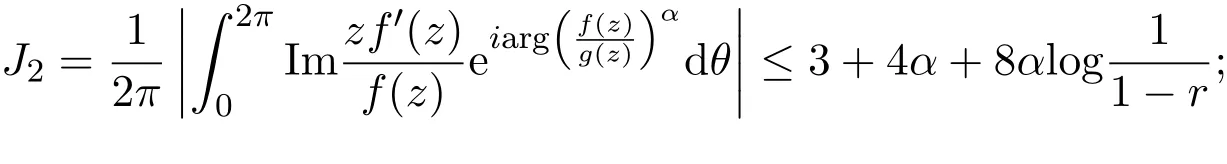
(3)

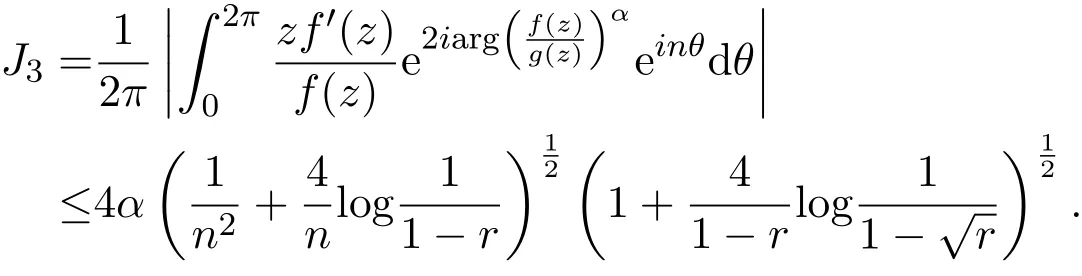
证明(1)由引理2.1和引理2.2可知，

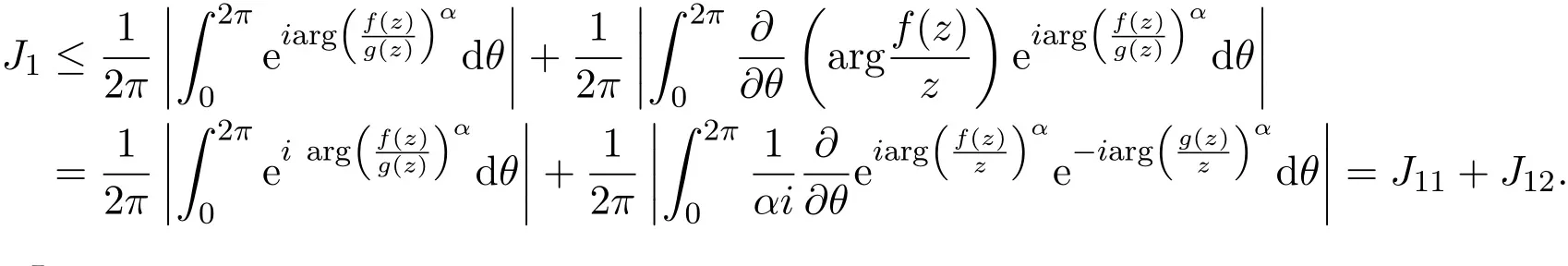
易知J11≤1，利用分部积分公式和引理2.4可得，

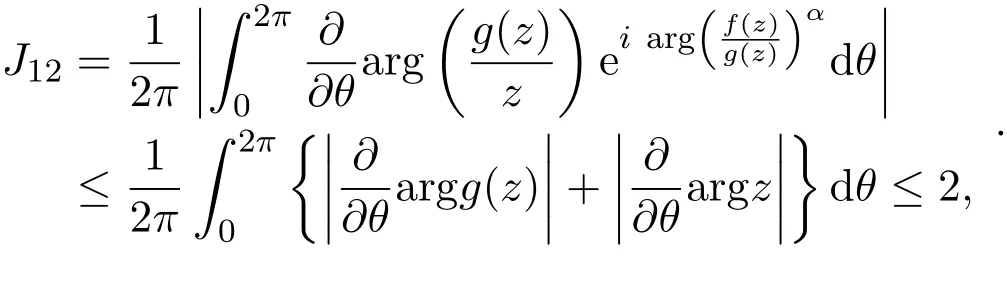
所以

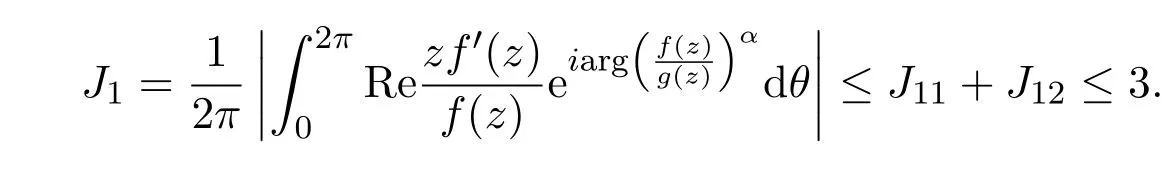
(2)记

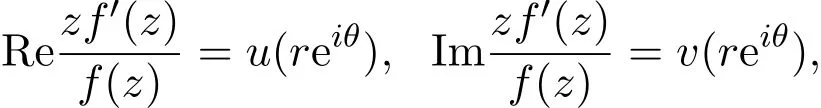
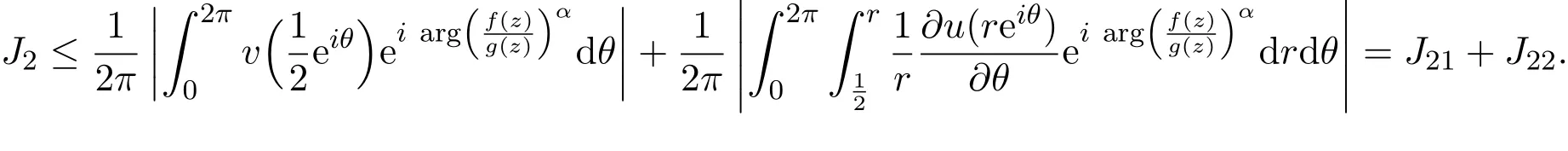
而

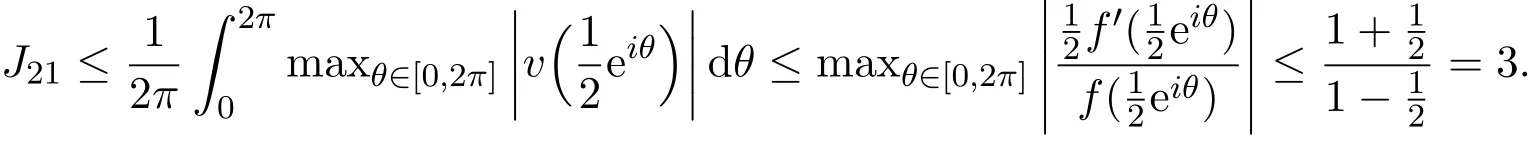
由分部积分和引理2.2可知，

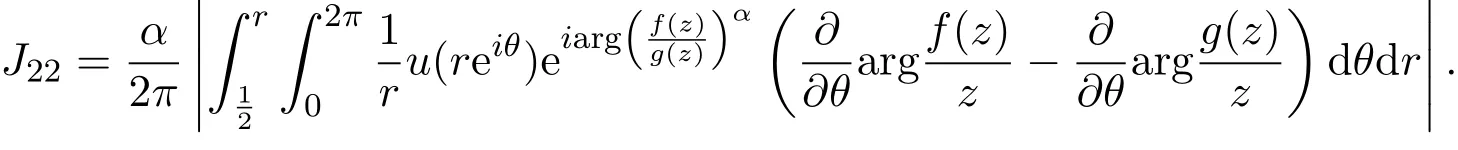
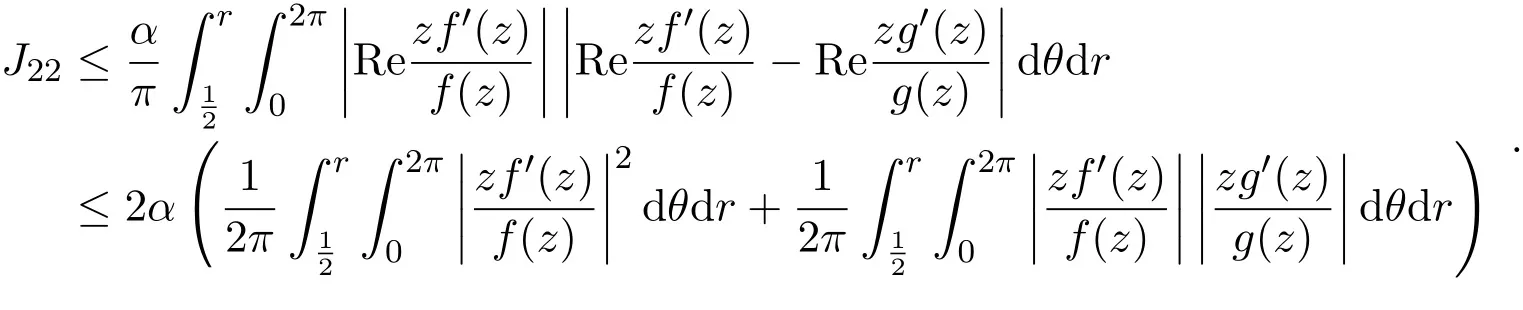
由引理2.3和Schwarz不等式可知，

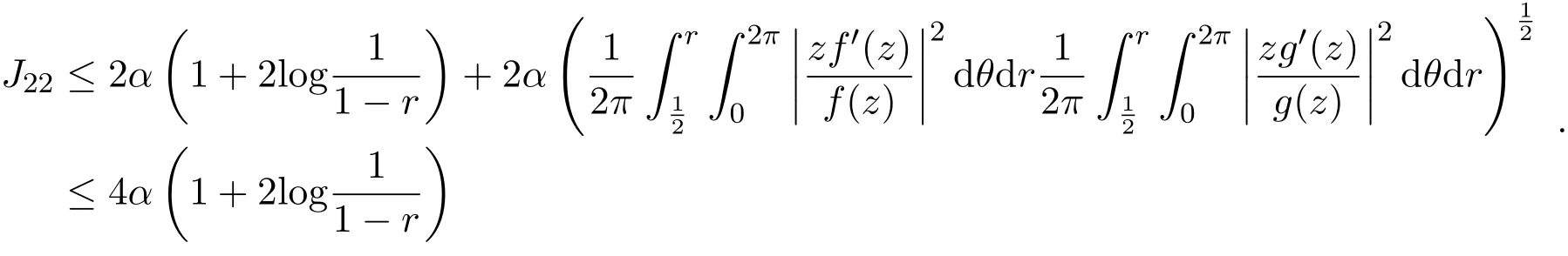
所以

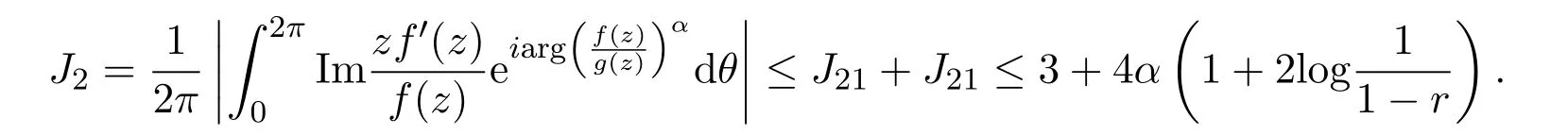
由(3)式和(2)式可知，

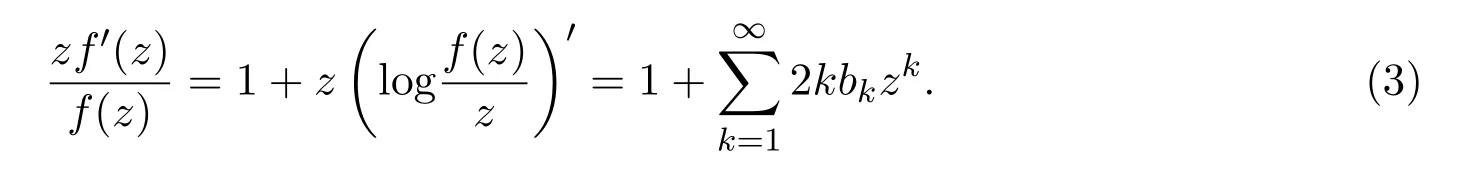
所以

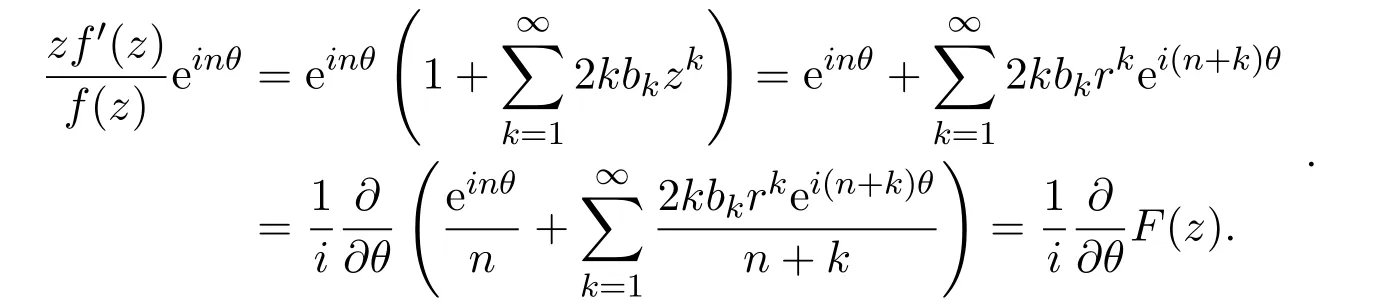
由引理2.1，引理2.2和分部积分可得，

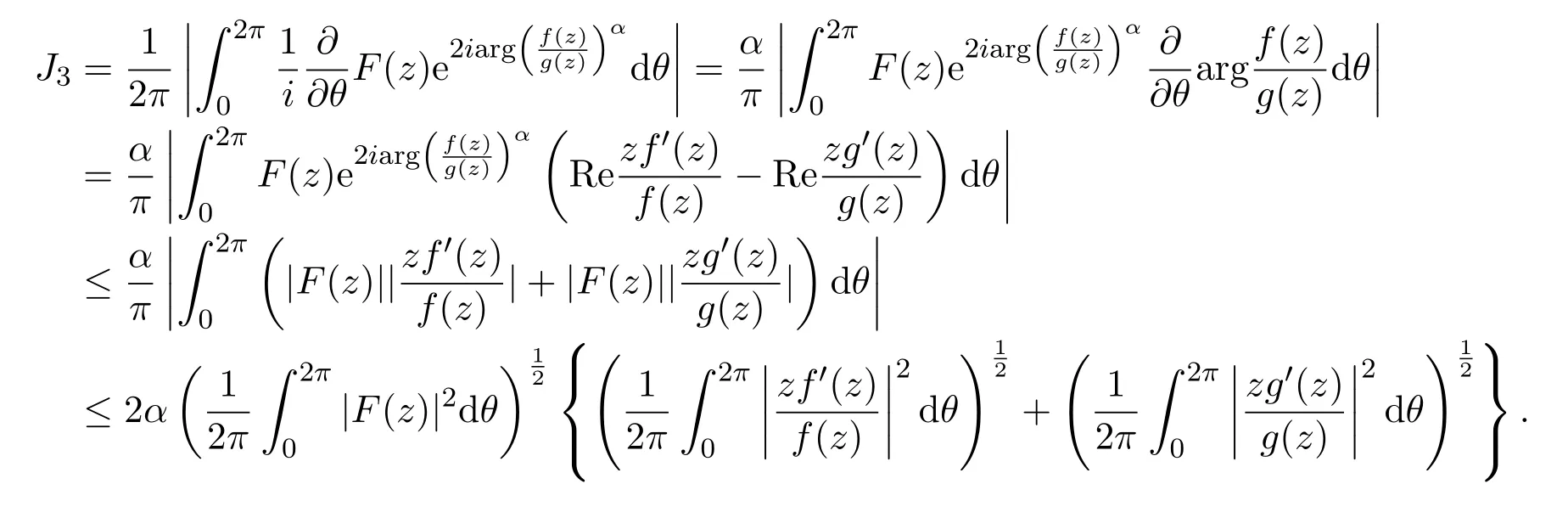
由引理2.5可知，

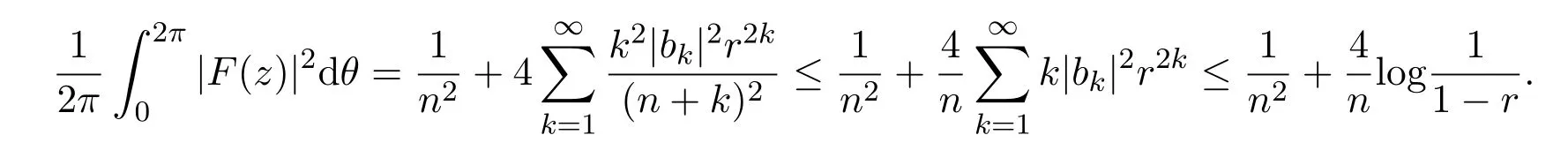
所以由引理2.3可知，

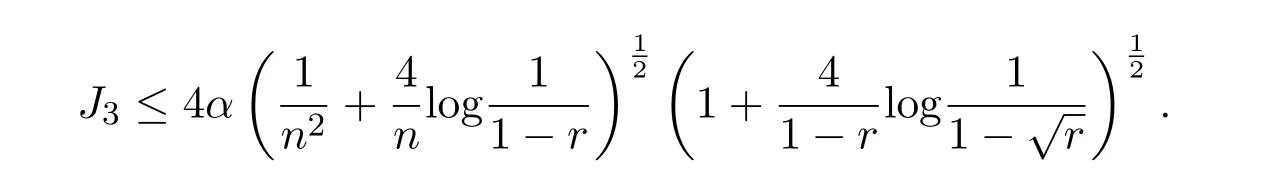
引理 2.7设f(z)∈Bα(β)(α≥0，0≤β＜1)，则对z=reiθ，0≤r＜1，有

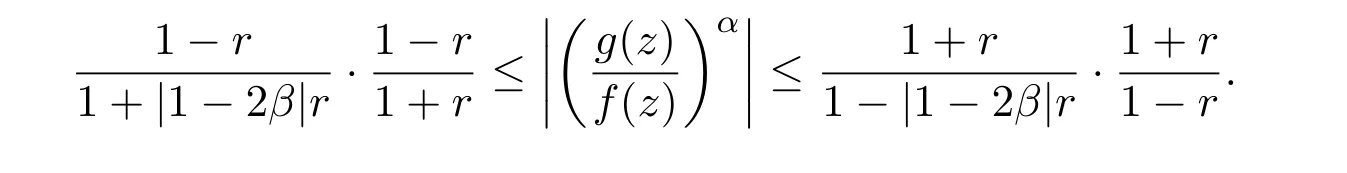
证明如果f(z)∈Bα(β)，则存在g(z)∈S∗使得(1)式成立.由于0≤β＜1，所以

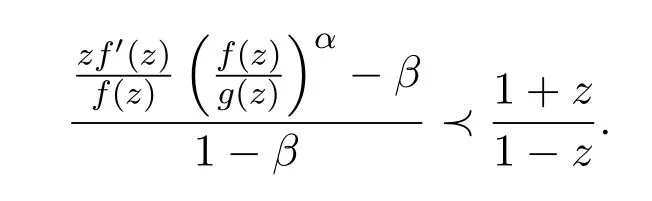
由从属关系定义可知，存在Schwarz函数ω(z)，使得

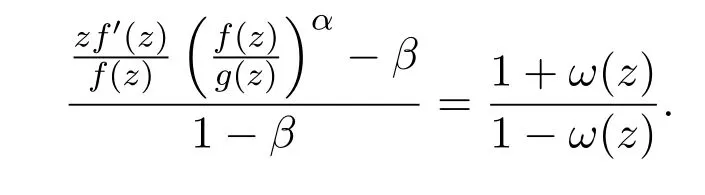
经简单计算有

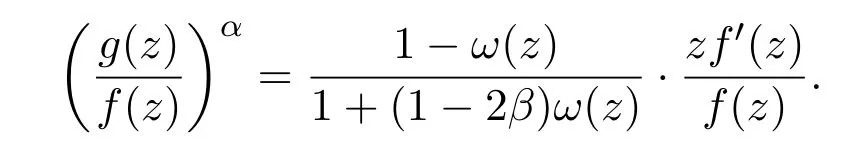
因为0≤β＜1，所以|2β-1|＜1，又因为|ω(z)|≤|z|，所以

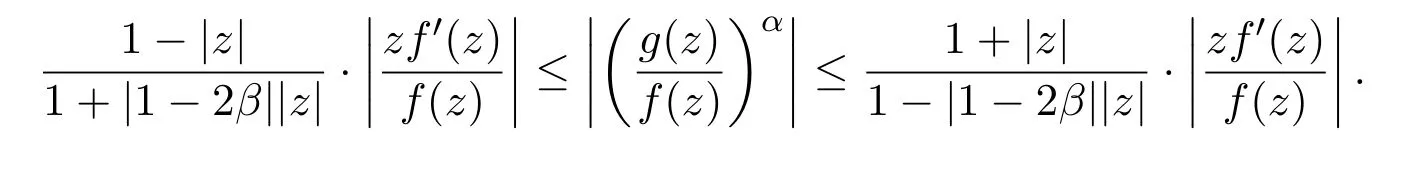
由于

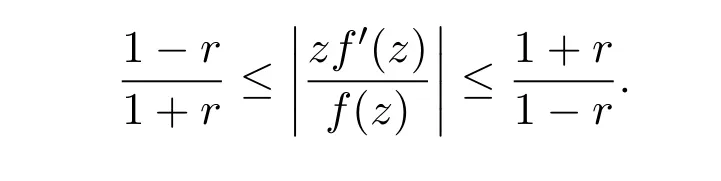
所以

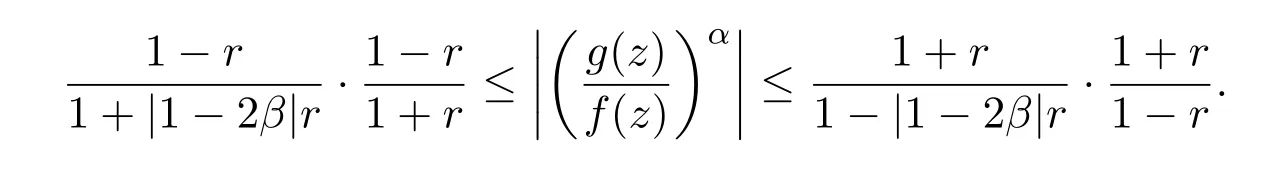
3　主要结论

定理 3.1设f(z)∈Bα(β)，则对n≥2，

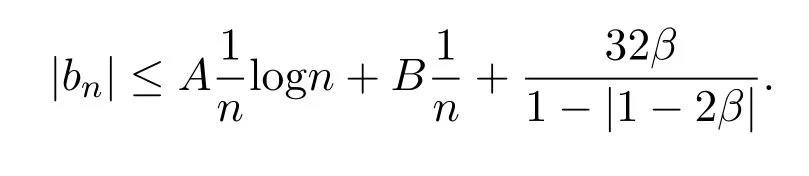
其中

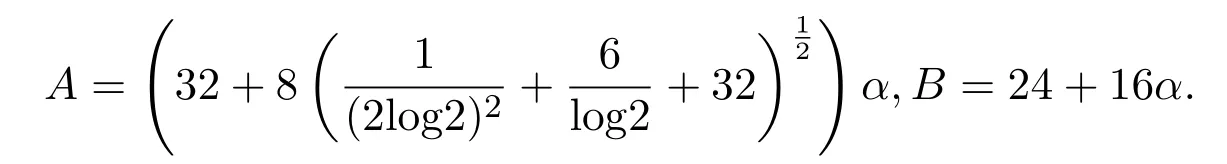
证明设f(z)∈Bα(β)，则存在g(z)∈S∗，使得(1)式成立.记

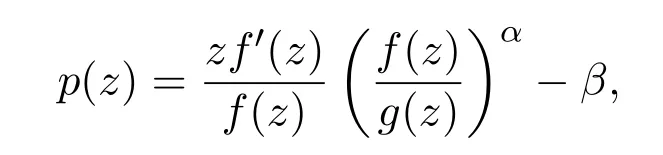
则Re p(z)＞0.由(3)式可知对z=reiθ，

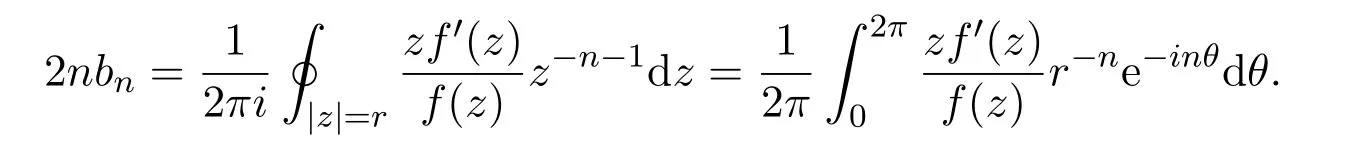
因此

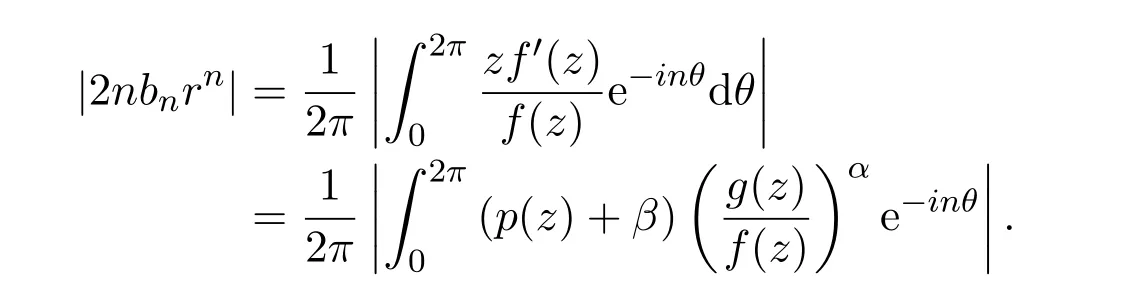
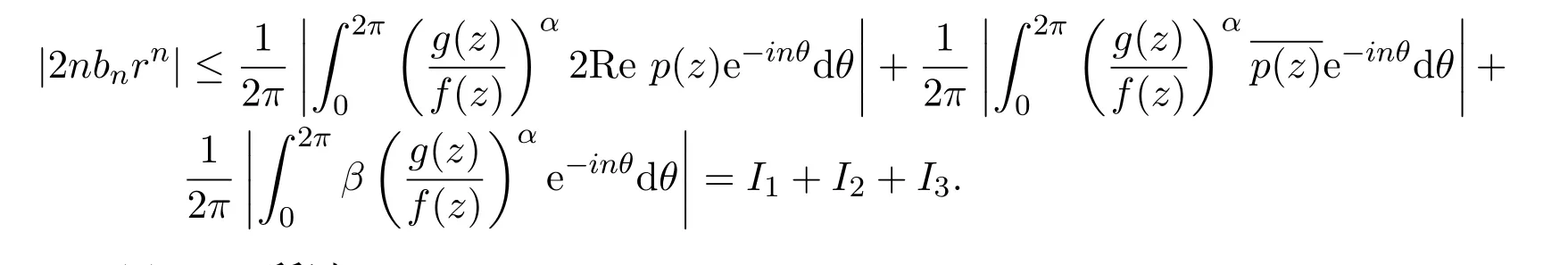
因为Re p(z)＞0，所以

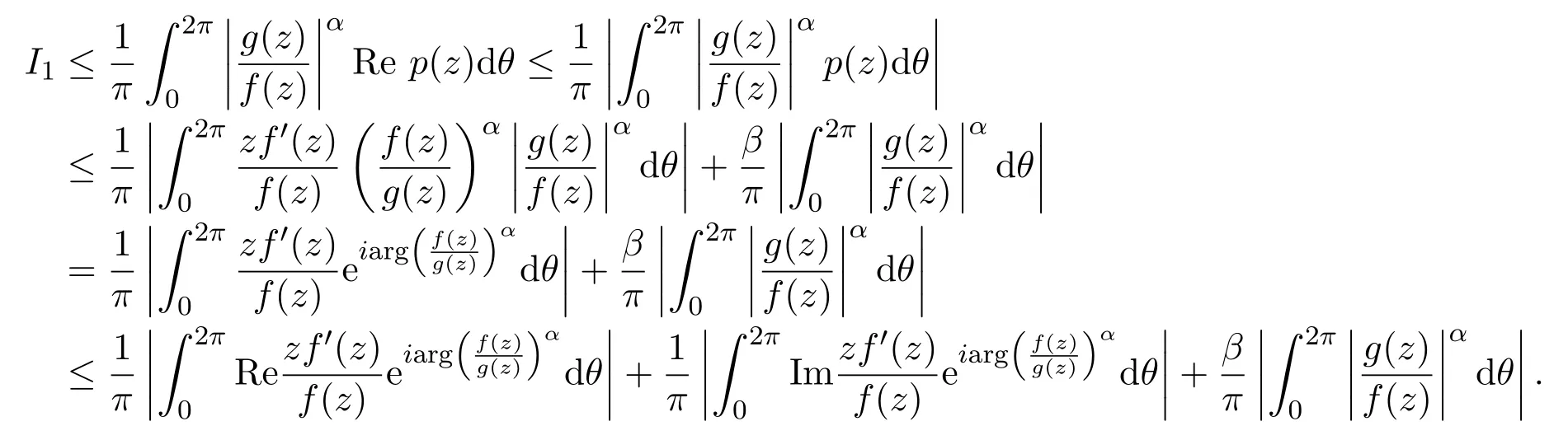
由引理2.6可知，

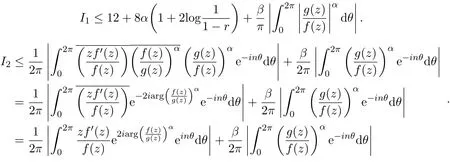
由引理2.6可知，

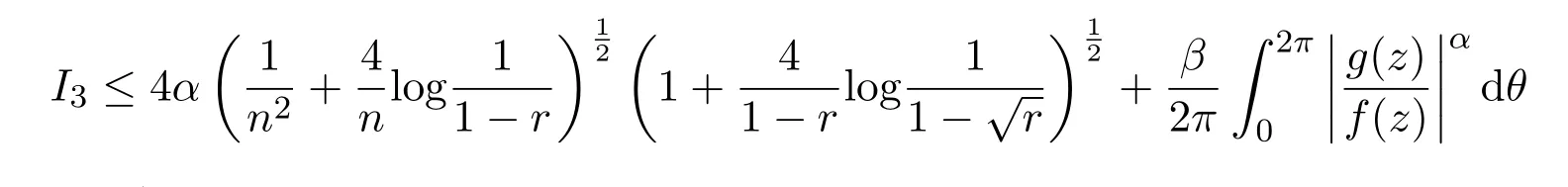
由引理2.7可知，

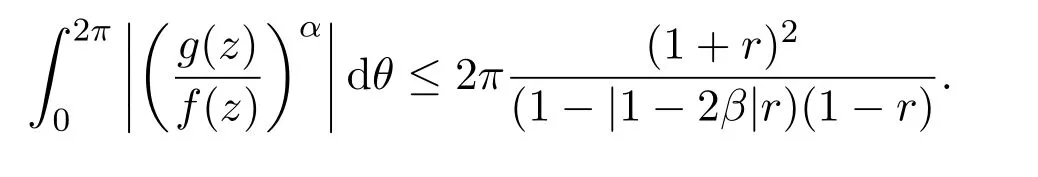
所以

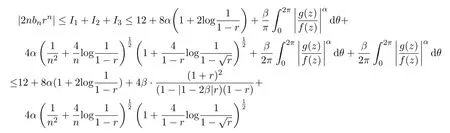
所以

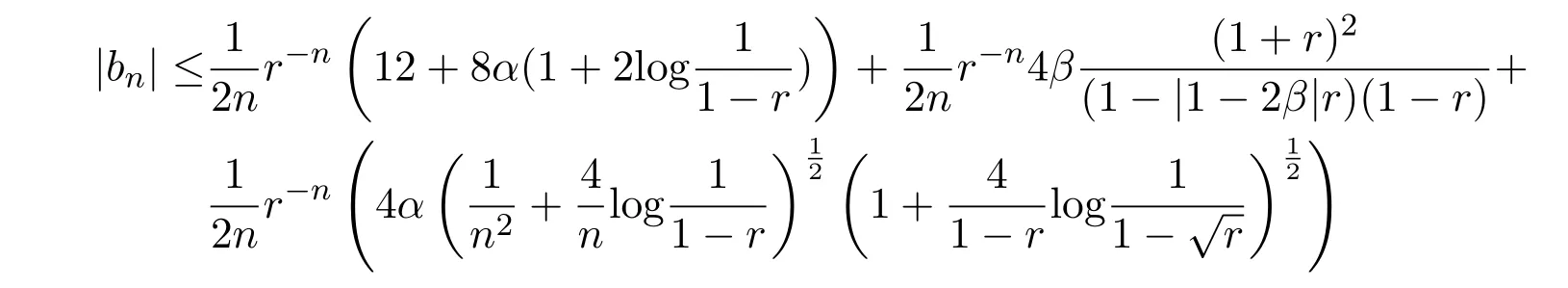
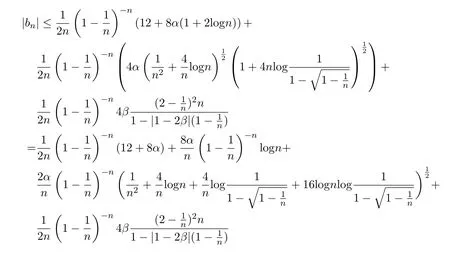
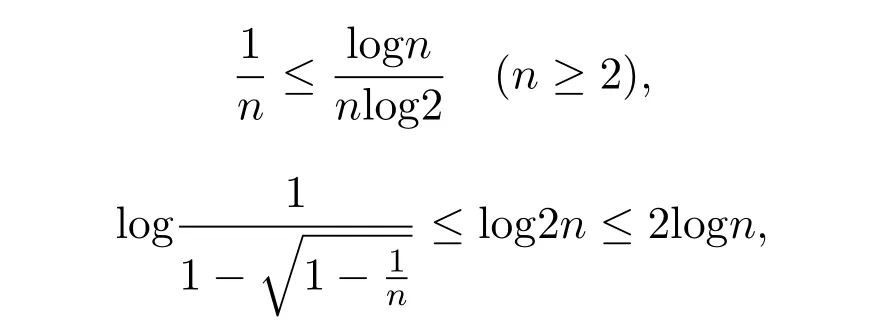
所以

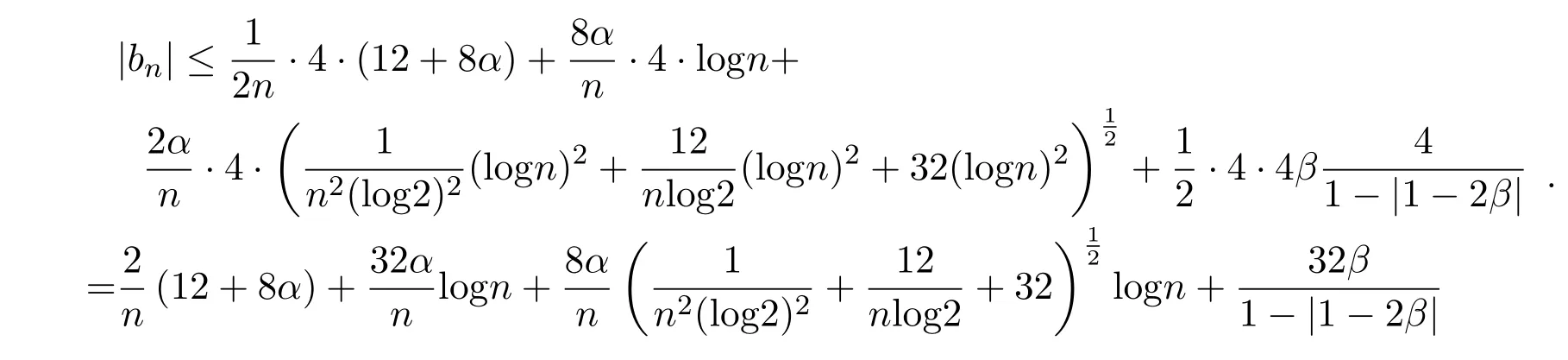
因为

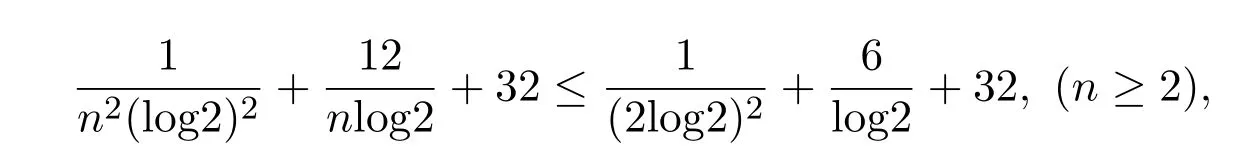
所以

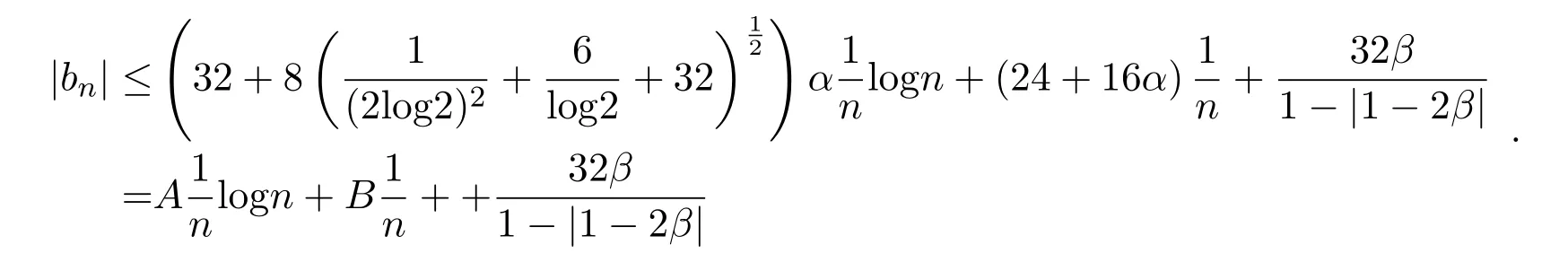
其中

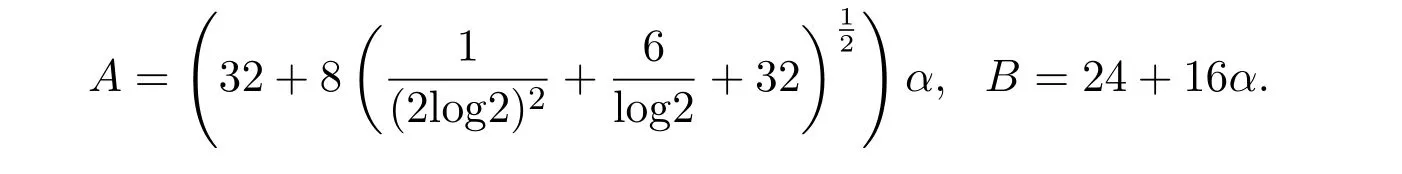
[1］Jenkins J A.On circularly symmetric functions[J］.Proceedings of the American Mathematical Society，1955，6（4）：620-624.

[2］Goel R M，Mehrok B S.A subclass of univalent functions[J］.Journal of the Australian Mathematical Society （Series A），1983，35（01）：1-17.

[3］Kim Y C.A note on growth theorem of Bazileviˇc functions[J］.Applied Mathematics and Computation，2009，208（2）：542-546.

[4］杨定恭.α型β级Bazileviˇc函数的Fekete-Szego问题[J］.数学研究与评论，1998，18（1）：99-104.

[5］胡克.单叶函数的若干问题[M］.武汉：武汉大学出版社，2001.

[6］YE Z.The logarithmic coefficients of close-to-convex functions[J］.Bulletin of the Institute of Mathematics Academia Sinica（New Series），2008，3（3）：445-452.

[7］Ye Z.The coefficients of Bazileviˇc functions[J］.Complex Variables and Elliptic Equations，2013，58（11）：1559-1567.

[8］叶中秋.圆对称函数的对数系数[J］.江西师范大学学报：自然科学版，2013，32（1）：6-8.

[9］Deng Q.On the logarithmic coefficients of Bazileviˇc functions[J］.Applied Mathematics and Computation，2011，217（12）：5889-5894.

[10］Pommerenke C H.Univalent Functions[M］.Gottingen：Vandenhoeck and Ruprecht，1975.

[11］Lebedev N A.An application of the area principle to non-overlapping domains[J］.Trudy Matematicheskogo Instituta im.V A Steklova，1961，60：211-231.

2010 MSC:30C45

The logarithmic coefficients of Bazileviˇc functions of type α and order β

Niu Xiaomeng，Li Shuhai
（School of Mathematics and Statistics，Chifeng University，Chifeng 024000，China）

By using subordination，the paper gives estimation of|（g（z）/f（z））α|.A nonnegative function and estimate the integration of model of a complex function have been constructed.The logarithmic coefficients bnof Bazileviˇc functions of type α and order β is discussed by this method.The results obtained generalize some known results.

univalent functions，logarithmic coefficients，Bazileviˇc functions

O174.51

A

1008-5513(2016)04-0342-09

10.3969/j.issn.1008-5513.2016.04.003

2016-04-27.

国家自然科学基金(11561001)；内蒙古自然科学基金(2014MS0101)；内蒙古高等学校科学研究项目(NJZY16251).

牛潇萌(1982-)，硕士，讲师，研究方向：复分析及应用.