基于平衡损失函数的具有时间效应的多合同信度模型

李新鹏,朱　坤，孙维霞，杨　丽，吴黎军

(新疆农业大学　a.数理学院; b.数学与系统科学学院， 乌鲁木齐　830052)



基于平衡损失函数的具有时间效应的多合同信度模型

李新鹏a,朱坤a，孙维霞a，杨丽a，吴黎军b

(新疆农业大学a.数理学院; b.数学与系统科学学院， 乌鲁木齐830052)

利用信度理论的方法，考虑制定的保费的公平性、合理性，以及各风险组之间具有特殊的相依效应(时间效应)，得到了平衡损失函数下具有时间效应的多合同模型的信度保费和多合同Bühlmann模型的信度保费，同时给出了结构参数的无偏估计，推广了经典信度理论。

多合同信度模型；平衡损失函数；时间效应

信度理论是精算学中最重要的保费厘定技术。它是用保单持有人过去的索赔额数据来计算保单组合的下一年保费的一种定价方法。现代信度理论起源于Bühlmann，它给出了任意分布下的净保费信度估计。信度保费为样本均值和聚合保费的加权和，其中权重因子被称为信度因子[1]。

给定保单的过去n年的索赔额X1,…,Xn，其分布依赖于风险参数Θ。由于风险的非其次性，假设Θ是随机变量，具有先验分布h(θ)。在Θ给定条件下，Xi(i=1,2,…,n)独立同分布，且分布函数为H(x,θ)。通过保单持有人的前n年索赔额X1,…,Xn来计算第Xi1,…,Xin年的保费。将保费估计值限定在过去索赔额的线性组合中，根据保单持有人的风险特征得到信度公式：

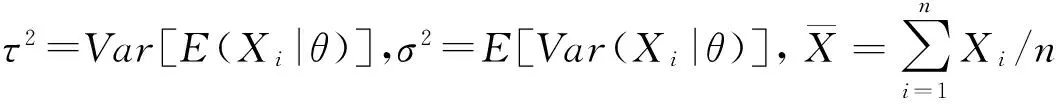
经典信度理论假定在风险参数给定下,一个保单组合的不同保单索赔额之间独立且同一个保单不同年索赔额之间也独立。但在实际应用中,各个保单间是具有风险相依结构的,如同一次交通事故可以导致多次索赔,地域临近的房屋面临共同的火灾风险等。郑丹等[2]利用信度理论的方法研究了具有时间变化效应的信度保费估计问题,得到了对应的信度保费。Bolancé等[3]研究了索赔频率风险模型，得到了时间效应为自相关时间序列时的信度保费。Frees等[4]在时间效应为Student-t copula条件下研究了信度保费的估计问题。温利民等[5]推广了Bühlmann和Bühlmann-Straub模型，研究了具有共同随机效应的信度模型，运用正交投影的方法，得到了信度保费。黄维忠等[6]就平衡损失函数下具有共同随机效应的信度保费问题进行了研究。

保险公司在制定下一年保费的时候，希望与保险人心目中的保费相差较小。因此，本文提出使用平衡损失函数，其既可以反映拟合优度，又能反映估计的精确性。设第i个保单的目标估计为δ0i(X)，它与过去的索赔数据有关，可以是保险公司认可的保费。因此，定义的平衡损失函数为：

(1)

0≤ω≤1为权重因子，其取值不同反映了目标保费与拟合程度的重要性不同。式(1)给出的平衡损失函数在ω=0时为经典信度理论中的平方损失函数。平衡损失函数在近些年来应用较广泛[6-8]。

本文既考虑了风险间的相关性,又考虑了保费制定的公平性、合理性。因此，运用平衡损失函数研究了风险组之间具有时间相依结构的多合同信度模型,得到了相应的信度保费。

1　模型假设与准备

考虑K个保单构成一个保单组合,对于第i个保单,它的过去n年索赔额为Xi1,…,Xin,假设每个保单各年索赔额都有各自的风险参数,为Θi1,…,Θin，且这些风险参数具有某种相关结构。假设如下:

假设1给定时间效应Θij=θ时，索赔额Xij间独立且同分布，且E(Xij|Θij)=μ(Θij)，Var(Xij|Θij)=σ2(Θij)，i=1,2,…,K，j=1,2,…,n+1。

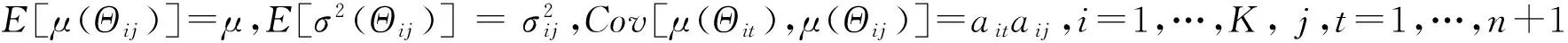
假设3本文使用的平衡损失函数为

为此，给出以下记号：

Xi=(Xi1,…,Xin)′，Θi=(Θi1,…,Θin)′

X= (X1′,…,XK′)′，Θ= (Θ1′,…,ΘK′)′

本文目标为求解最优化问题：

(2)

引理1给出了具有时间效应的多合同信度模型的重要性质。

引理1在假设1和假设2下，有以下结果[9]：

①Xij的均值为

② 过去索赔和未来索赔的协方差为

③Xi的协方差矩阵为

④Xi的协方差矩阵的逆为

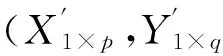
2　平衡损失函数下多合同信度模型的保费估计

定理1为最优化问题(2)的解，即第个保单下一年的信度保费估计。

定理1在上述3个假设条件下，运用平衡损失函数，通过求解最优化问题(2)，得到Xi,n+1的最优信度保费估计为：

其中：

证明引入一随机变量Yi=Iδ0i(X)+(1-I)Xi,n+1，其中I为0-1区间的随机变量，它独立于其他的随机变量且P(I=1)=1-P(I=0)=ω。ω为式(2)中的权重因子。因此，最优化问题(2)等价于

(3)

由引理2知，最优化问题(3)的解为：

μYi=EYi=E[E(Yi|I)]=

ωE(Yi|I=1)+(1-ω)E(Yi|I=0)=

ωE[δ0i(X)]+(1-ω)EXi,n+1=

ωμδ+(1-ω)μ

又因为E(Xi|I)=E(Xi)为一常数向量，所以Cov[E(Yi|I),E(Xi|I)]=0。由引理1知：

ΣYiXi=Cov(Yi,Xi)=E[Cov(Yi,Xi|I)]+

Cov[E(Xi|I),E(Yi|I)]=

ωCov(Yi,Xi|I=1)+

(1-ω)Cov(Yi,Xi|I=0)=

ωCov(δ0i(X),Xi)+

(1-ω)Cov(Xi,n+1,Xi)=

ωdii1n′ + (1-ω)ai,n + 1(ai1,…,ain)

1n为n×1的全1向量，且

因此，

所以，Xi,n+1的最优估计为：

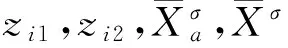
结构参数σ2的无偏估计为

结构参数a2的无偏估计为

3　结束语

本文在平衡损失函数下研究了具有时间效应的多合同信度模型,得到了相应的信度保费,推广了经典的信度理论,且基于所得结论给出了平衡损失函数下多合同Bühlmann模型的信度估计和基本结构参数μ,σ2,a2的无偏估计。

[1]BÜHLMANN H,GISLER A.A course in credibility theory and its applications[M].Netherlands:Springer,2005.[2]郑丹,章溢,温利民.具有时间变化效应的信度模型[J].江西师范大学学报(自然科学版),2012,36(3):249-252.

[3]BOLANCÉ C,GUILLÉ M,PINQUET J.Time-varying credibility for frequency risk models:estimation and tests for autoregressive specification on the random effects[J].Insurance:Mathematics and Economics,2003,33(2):273-282.

[4]FREES E W,WANG P.Credibility using copulas[J].North American Acturial Journal,2005,9(2):31-48.

[5]WEN L M,WU X Y,ZHOU X.The credibility premiums for models with dependence induced by common effects[J].Insurance:Mathematics and Economics,2009,44(1):19-25.

[6]HUANG W Z,WU X Y.The credibility premiums with common effects obtained under balanced loss functions[J].Chinese Journal of Applied Probability and Statistics,2012,28(2):203-216.

[8]李新鹏,吴黎军.平衡损失函数下具有时间变化效应的信度保费[J].重庆理工大学学报(自然科学),2013,27(4):133-137.

[9]郑丹.相依风险下的信度模型[D].南昌:江西师范大学,2013.

(责任编辑陈艳)

Multiple Contracts Model with Time Effects Based on Balanced Loss Function

LI Xin-penga, ZHU Kuna, SUN Wei-xiaa, YANG Lia, WU Li-junb

(a.College of Mathematics and Physics; b.College of Mathematics and System Sciences,Xinjiang Agriculture University, Urumqi 830052, China)

Using the credibility theory method, and considering the premium’s equity, various risk groups’ dependent effects, i.e. time effects, this paper obtained the multiple contracts model’s premium with time effects under balanced loss function, and derived the multiple contracts Bühlmann model’s premium, and gave the unbiased estimation of structure parameter, thus generalized the classical credibility theory.

multiple contracts model; balanced loss function; time effect

2015-10-10.

国家自然科学基金资助项目(11361058)；新疆维吾尔自治区大学生创新训练项目(201510758112)

李新鹏(1986—),男,甘肃人,硕士,讲师,主要从事精算数学研究，E-mail:news20060801015@126.com。

format：LI Xin-peng, ZHU Kun, SUN Wei-xia,et al.Multiple Contracts Model with Time Effects Based on Balanced Loss Function[J].Journal of Chongqing University of Technology(Natural Science)，2016(8):165-168.

10.3969/j.issn.1674-8425(z).2016.08.027

O212

A

1674-8425(2016)08-0165-04

引用格式：李新鹏,朱坤，孙维霞，等.基于平衡损失函数的具有时间效应的多合同信度模型[J].重庆理工大学学报(自然科学)，2016(8):165-168.