设计因素对RC框架结构地震易损性的影响①
郑 捷,左河山,李文博,雷振东,郑山锁
(西安建筑科技大学建筑设计研究院,陕西 西安 710055)
设计因素对RC框架结构地震易损性的影响①
郑捷,左河山,李文博,雷振东,郑山锁
(西安建筑科技大学建筑设计研究院,陕西 西安 710055)
考虑到结构抵抗地震作用的机制为结构和地震动的不确定性与非线性相互耦合的过程,采用增量动力分析(IDA)考虑地震动的不确定性,选取16条地震动记录,基于OpenSEES的有限元建模理论对13榀平面RC框架结构进行基于IDA方法的地震易损性分析,分别讨论轴压比、高宽比、混凝土强度以及纵筋强度等结构参数对RC框架结构抗震性能的影响。结果表明:柱轴压比对结构抗震性能的影响显著,而高宽比对结构抗震性能的影响不明显;在保证柱轴压比相近的前提下,提高柱混凝土强度能够提升结构的抗震性能;相同地震作用下梁柱配置纵筋强度较高的框架结构达到立即使用(IO)状态和生命安全(LS)状态的概率较配置纵筋强度较低的大,配置纵筋强度较高的框架结构较配置纵筋强度较低的表现出更好的抗倒塌能力。
RC框架结构; 轴压比; 地震易损性; 抗倒塌能力
0 引言
结构抵抗地震作用的机制为结构和地震动不确定性与非线性相互耦合的过程[1],虽然与地震动的不确定性相比,结构的不确定性对结构抗震性能的影响不占主导作用,但结构自身的不确定性,如结构计算模型、结构和构件尺寸、材料强度等对结构抗震性能的影响是不能忽视的。鉴于此,本文通过对13榀RC平面框架结构的地震易损性分析,讨论轴压比、高宽比、混凝土强度以及纵筋强度这四种不确定性因素对RC框架结构抗震性能的影响。
1 RC框架结构的计算模型
合理地建立构件和结构力学分析模型是结构进行增量动力分析的关键环节,是准确模拟实际结构在地震激励时构件受力、变形情况的基础。作为科学研究型软件的代表,OpenSEES软件能较好地模拟RC框架结构在地震激励下响应的全过程,因此本文以OpenSEES软件为平台进行数值模拟[2]。
依据现行《建筑抗震设计规范》(GB50011-2010)和《混凝土结构设计规范》(GB50010-2010),采用通用结构设计软件PKPM进行RC框架结构设计。首先设计了一榀3跨6层钢筋混凝土框架结构,平面布置规则对称,首层层高为3.6 m,二层及以上层高均为3.3 m,总高度20.1 m,混凝土强度等级采用C35,梁柱纵向钢筋为HRB400,箍筋为HPB300,作为模型1。在模型1的基础上分别设计四组对比模型,各模型参数见表1~表4。模型均位于西北某省会城市,抗震设防烈度Ⅷ度(0.2g),地震分组为第一组,场地类别为Ⅱ类,地表粗糙类别为B类,基本雪压取0.3 kN/m2,不考虑风荷载的作用。

表1 轴压比变化模型参数

表2 高宽比变化模型参数

表3 柱混凝土强度平均值及弹性模量

表4 梁柱纵筋强度平均值
各层楼板厚均取120 mm,楼面恒载取5.3 kN/m2,屋面恒载取7.0 kN/m2,活载均取2.0 kN/m2。由于本文设计的结构力学模型在平面和立面上对称,所以采用OpenSEES建模时将结构的空间框架模型简化为平面框架模型,建模与分析时选取一榀平面框架进行,楼层重量按照1.0恒载+0.5活载折算。结构平面布置与计算单元选取如图1所示。

图1 结构平面布置与计算单元选取示意Fig.1 Layout plan of structure and selected calculation unit
采用OpenSEES软件对结构进行非线性分析,材料强度均取平均值[3]以反映真实受力状态。针对本文的RC平面框架结构,采用以下材料本构模型:混凝土采用Concrete02模型(基于Kent-Scott-Park模型);钢筋采用Steel02模型。截面模型采用纤维模型,其主要思路是沿着单元纵向将各分析截面离散化为若干小纤维(包括混凝土纤维和钢筋纤维)。单元模型采用非线性梁柱单元,该单元允许刚度沿杆件长度变化,通过确定单元控制截面的各截面抗力和截面刚度矩阵,按照Gauss-Lobatto积分方法计算单元抗力和切线刚度矩阵[4]。
2 基于IDA方法的RC框架结构地震易损性分析
2.1地震波选取
地震动,即地震地面运动,是由震源释放出来的地震波引起的地表附近土层的震动,是引起震害的外因和连接地震与结构抗震之间的桥梁。本文所选全部模型均处于Ⅱ类场地,与美国地震勘测中心(USGS)对场地划分中的S2场地相似,vse取180~360 m/s。参考ATC-63选波原则[5],从PEER Strong Motion Database中选取16条满足波速范围和震中距要求的地震记录,如表5所列,持时取20 s。

表5 分析输入的地震动记录
根据规范的具体规定按式(1)比例进行调整(放大或缩小),波形不变。

(1)
2.2极限状态定义
美国FEMA356[6]定义了三个性态点:立即使用(Immediate Occupancy,IO)、生命安全(Life Safe,LS)和防止倒塌 (Collapse Prevention,CP)。依据DM准则,本文选取最大层间位移角θmax作为结构损伤指标DM,FEMA356中RC框架结构不同性态水平的层间位移角限值如表6所列。注意到DM准则在判断倒塌极限点会出现一个倒塌失效值CDM对应多个倒塌极限状态点的情况,本文在确定CP性能点时按照IM准则,即以初始斜率的20%和层间位移角为10%中对应IM值较小的点作为倒塌极限点。

表6 FEMA 356定义的不同性态水平的层间位移角限值
2.3结构地震易损性理论推导
文献[7]指出结构工程需求参数(EDP)样本与地震动参数(IM)之间的关系满足公式:
EDP=α(IM)β
(2)
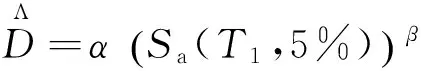
(3)
两边取对数:

(4)
结构反应的概率函数D用对数正态分布函数表示,其统计参数为:
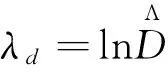
(5)

(6)
式中:λd为D的对数平均值,βd为D的对数标准差。
同理,假设结构能力参数的概率函数C也能够用对数正态分布函数来表示,该函数由结构能力参数对数平均值λc和对数标准差βc两个参数来定义。式(4)中a=lnα、b=β,其中a、b通过对结构进行大量增量动力分析后的数据进行统计回归得到,则α、β值即可容易求出。
结构的易损性曲线表示在不同强度地震作用下结构反应D超过破坏阶段所定义的结构能力参数C的条件概率。其公式可表示为:
Pf=P(C/D<1)
(7)

结构的失效概率可直接通过Z<0的概率来表达[8],即:

(8)
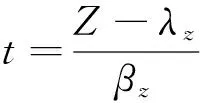
式(8)可写成:

(9)
特定阶段的失效概率Pf为:

(10)

2.4基于IDA方法的地震易损性分析基本步骤
(1)建立模拟结构在地震激励下动力响应主要特征的有限元分析模型。
(2)选择符合结构所处场地条件的地震动记录,并确定比例系数SF,选择合适的地震动强度指标IM和结构损伤指标DM。本文选定:IM为阻尼比为5%结构基本周期对应的加速度谱值Sa(T1,5%),DM为楼层最大层间位移角θmax。
(3)取一条地震动记录进行调幅,以首次调幅后的加速度进行一次弹塑性动力时程分析,记录分析结果得到的点(Sai,θi)记为P1,将此点与原点连线的斜率记为Ke,则Ke即为初始斜率。对该条地震动记录按一定的算法进行调幅,再次进行弹塑性动力时程分析,得到第二个点(Sa(i+1),θ(i+1)),记为P2。连接P1和P2,如果该线的斜率小于0.2 Ke(小于0.2 Ke时数值出现发散),则认为结构发生倒塌,往前搜索倒塌极限点。否则按多个等级调幅,继续计算下去,如果θi+1大于0.1,最大层间位移角限值取0.1作为倒塌极限点。
(4)以结构损伤指标DM为x坐标,地震动强度指标IM为y坐标,将弹塑性动力时程分析获得的与地震强度相关的结构性能参数点进行插值得到相应的单条IDA曲线,并在IDA曲线上定义极限状态点。
(5)重复步骤(3)、(4)即可得到多条地震动记录下的结构响应曲线,即多条IDA曲线。
(6)对多条IDA曲线进行统计得到16%、50%和84%分位值的百分位IDA曲线,并在三条百分位IDA曲线上定义极限状态点。
(7)通过对结构IDA分析响应数据进行线性回归,建立以地震动参数为自变量的结构反应的概率需求函数。
(8)求出不同地震动强度下结构达到极限状态的失效概率,绘制以所选地震动参数为变量的地震易损性曲线。
3 参数对结构地震易损性的影响
3.1轴压比对结构地震易损性的影响
现今设计人员多为了满足建筑外形以及业主对材料、空间等方面的要求,往往采用轴压比限值来确定框架结构柱截面尺寸,导致许多框架底层柱截面尺寸偏小,从而使得柱端抗弯承载力较小,不利于保证“强柱弱梁”的破坏机制。在遭遇罕遇地震作用时造成柱端先于梁端屈服而产生塑性铰,形成柱铰机构,削弱了结构的抗震能力,这一点在汶川地震中表现的特别突出。
对比图2(a)、(b)中模型1~模型5的地震易损性曲线可知,随着轴压比的增大,相同地震动强度下结构达到IO状态、LS状态的概率越大。也就是说结构轴压比越大,相同地震动强度下结构越容易发生轻微破坏和严重破坏。各结构在罕遇地震作用下倒塌率分别为0.5%、0%、0%、2.7%以及3.40%。ATC-63报告建议:“在设防大震下倒塌概率小于10%即认为结构达到大震性能的要求”。可见5个轴压比模型在罕遇地震激励下倒塌率均小于10%,即严格按我国现行规范设计的5个RC框架结构都能达到“大震不倒”的设防目标。若遇到像汶川地震那样的特大地震,地震动强度是规范规定设计强度的数倍,本处取Sa(T1)/Sa(T1)MCE=2进行研究。从图3中可知,轴压比最大的模型5的倒塌概率已经达到57.8%,而轴压比最小的模型3的倒塌概率只有1.2%,发生倒塌的概率仍很小。另外,增大柱截面面积,柱轴压比降低,结构的抗倒塌能力增强。

图2 结构IO及LS状态地震易损性曲线Fig.2 Seismic fragility curves of structures in IO and LS state

图3 不同轴压比结构的倒塌概率曲线Fig.3 Collapse probability curves of structures with different axial compression ratio
文献[9]对比了美国ATC、ACI、AEAOC(加州抗震规范)与新西兰NZS3101、欧洲EC8、菲律宾等国规范中关于轴压比限值的规定,发现中国规范所规定的轴压比限值明显偏大,直接导致按照轴压比限值确定的柱截面尺寸偏小,结构整体延性不足,不易形成“强柱弱梁”屈服机制。因此结合本节分析结果,建议我国规范合理地减小轴压比限值。
3.2高宽比对结构地震易损性的影响
房屋的高宽比是指房屋的总高度与总宽度(最小宽度)的最大比值,是建筑结构刚度、整体稳定、承载能力和经济合理性的宏观控制指标。本节通过变化结构总高度来调节结构高宽比,层数分别取4层、6层、8层以及10层。
对比图4(a)、(b)中模型1、模型6~8的地震易损性曲线可见,相同地震动强度下不同高宽比结构达到IO状态、LS状态的概率差异不显著,其中10层框架结构(高宽比最大)的失效概率相对稍大。从图5可见,在罕遇地震作用下4层、6层、8层以及10层框架结构倒塌概率分别为0.5%,0%,2.7%及2.02%。ATC-63报告建议:“在大震设防下倒塌概率小于10%即认为达到大震性能的要求”。鉴于4个不同高宽比模型在罕遇地震下倒塌率均小于10%,故严格按我国现行规范设计的5个RC框架结构都能达到“大震不倒”的设防目标。从图中并不能很直观地看出随着高宽比的增加结构抵御倒塌能力的变化规律。研究显示,随着高宽比的增加,柱截面尺寸也不同程度地增大,使得柱的抗倒塌能力增强,抵消了高宽比增加对结构抗震性能带来的不利影响,且IO状态、LS状态结构能力参数都是按DM准则统一取值,所以在相同的地震动强度下4层、6层、8层以及10层框架结构达到立即使用状态与生命安全状态的概率比较接近,因此并不能简单地认为,随着结构高宽比的增加结构的抗倒塌能力降低。
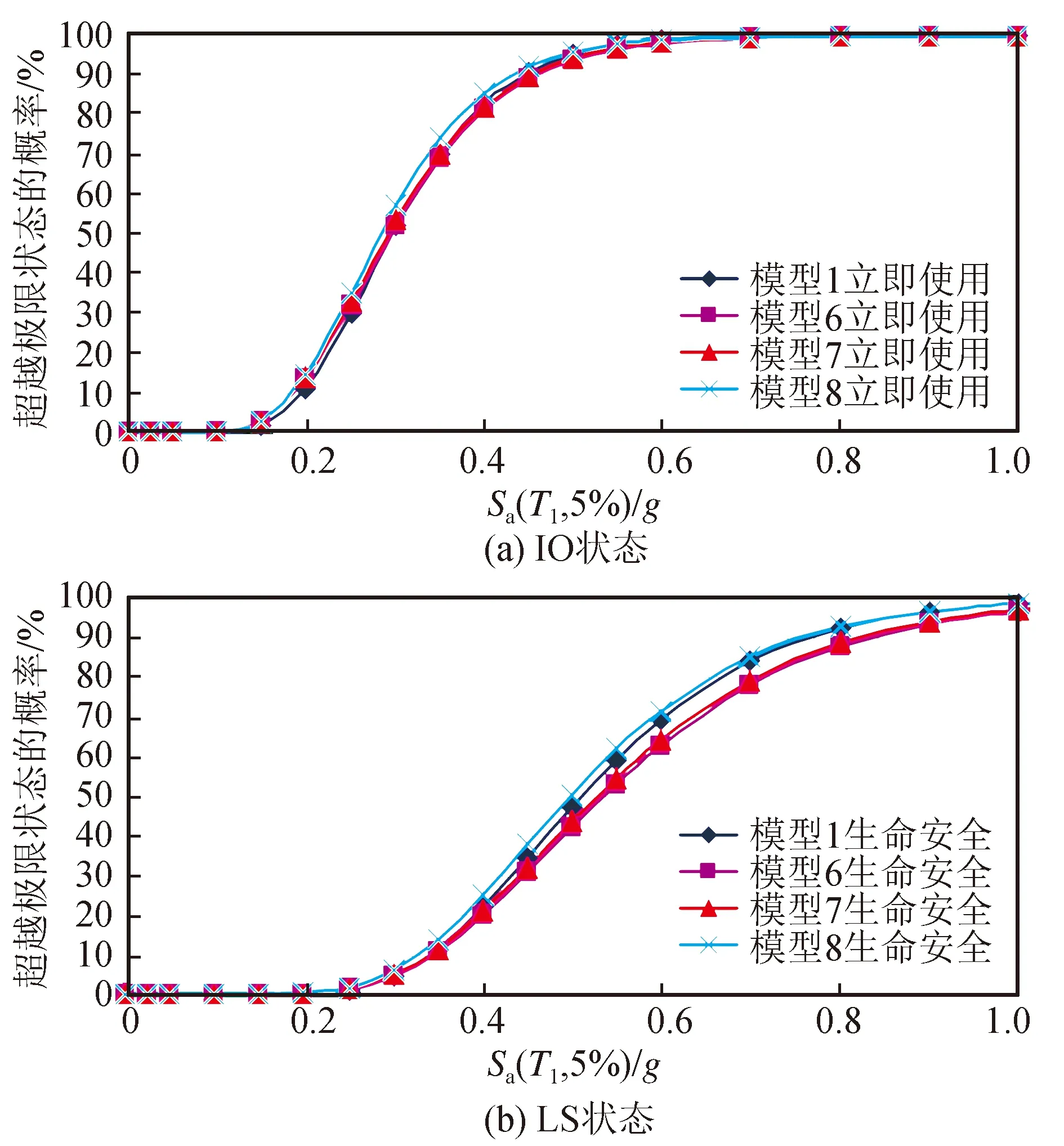
图4 结构IO及LS状态地震易损性曲线Fig.4 Seismic fragility curves of structures in IO and LS state

图5 不同高宽比结构的倒塌概率曲线Fig.5 Collapse probability curves of structures with different hight-width ratio
3.3混凝土强度对结构地震易损性的影响
在保证各RC框架结构最大轴压比近似相等的前提下,框架梁柱混凝土强度等级分别取C30、C35、C40和C50,以考察混凝土强度变化对结构地震易损性的影响。
对比图6(a)、(b)中模型1、模型9~11的地震易损性曲线可见,随着混凝土强度的提高,相同地震动强度下RC框架达到IO状态、LS状态的概率越小,即框架柱混凝土强度越低,相同地震动强度下结构越容易发生轻微破坏和严重破坏。由图7可见,随着柱混凝土强度的增大,框架结构的抗倒塌能力相应提高。
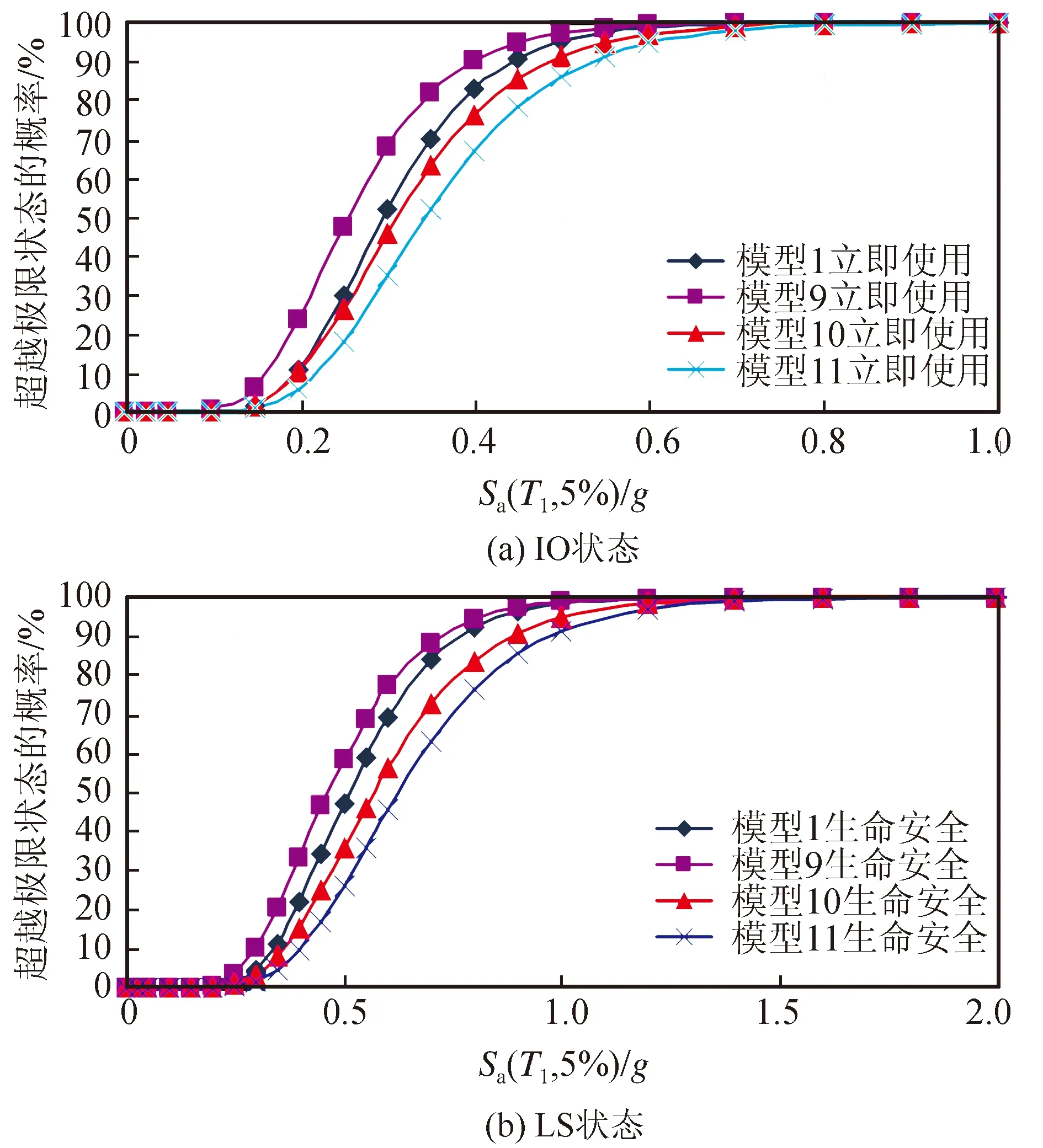
图6 结构IO及LS状态地震易损性曲线Fig.6 Seismic fragility curves of structures in IO and LS state

图7 不同混凝土强度结构的倒塌概率曲线Fig.7 Collapse probability curves of structures with different concrete strength
3.4纵筋强度对结构地震易损性的影响
HRB400级钢筋在《混凝土结构设计规范》(GB50010-2002)中明确为建筑用首选钢筋,但HRB500级钢筋由于缺乏相应的试验和研究资料一直未能进入规范,直到《混凝土结构设计规范》(GB50010-2010)颁布实施,才明确指出梁柱纵筋应采用HRB400和HRB500级钢筋[10]。按照我国现行规范设计了3个不同梁柱配筋的RC框架结构,其梁柱纵筋强度分别取HRB335、HRB400和HRB500的强度。
对比图8(a)、(b)可见,模型1、模型12和模型13达到IO状态和LS状态的地震易损性曲线有一定的差异,其中模型13(HRB500级钢筋)较其他两个模型的失效概率相对较大,即配置HRB500级钢筋的结构较容易发生轻微破坏和严重破坏。由图9可见,随着框架梁柱纵筋强度的增大,结构抗倒塌的能力相应增强。

图8 结构IO及LS状态地震易损性曲线Fig.8 Seismic fragility curves of structures in IO and LS state
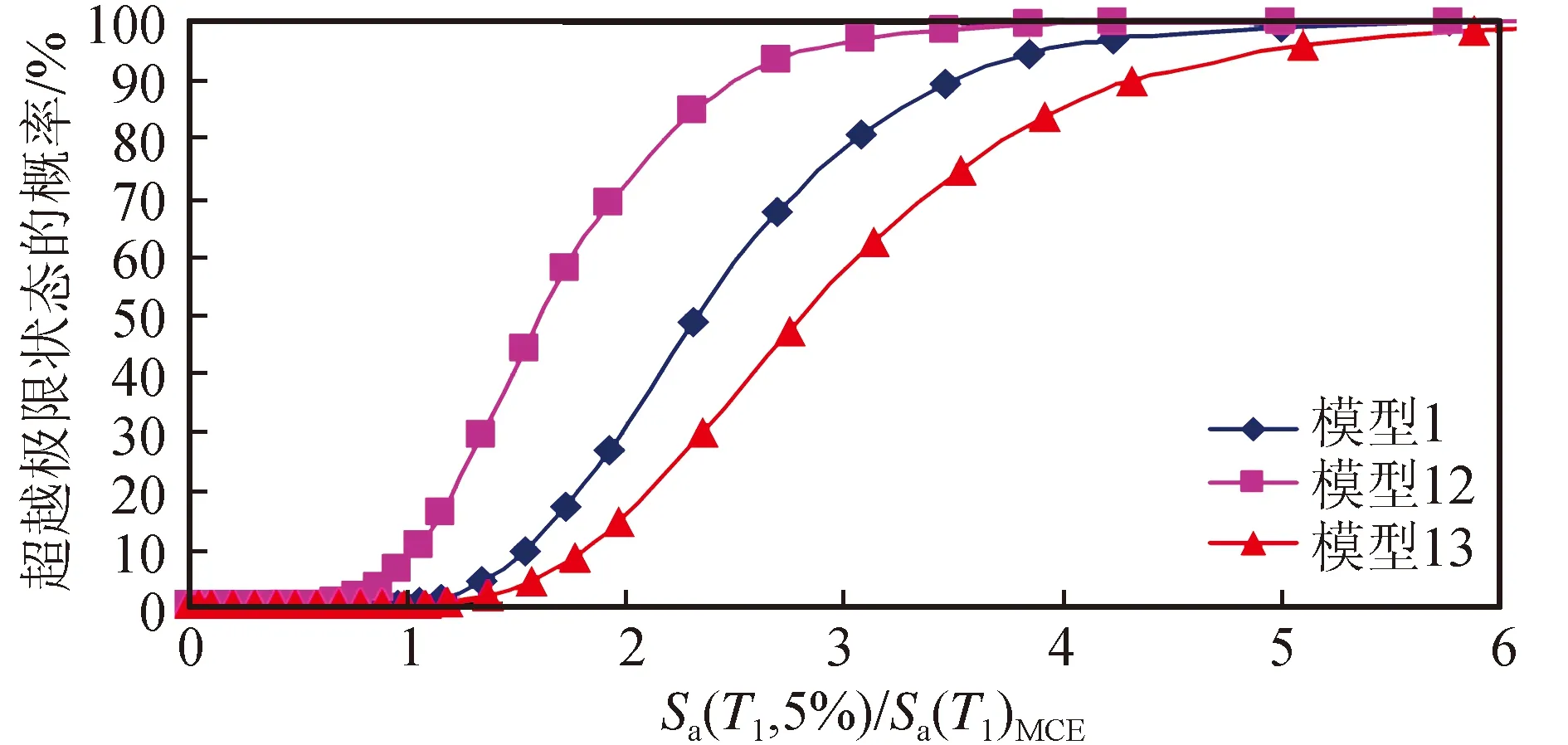
图9 不同梁柱纵筋强度的倒塌概率曲线Fig.9 Collapse probability curves of structures with different longitudinal reinforcement strength
4 结论
本文通过对13榀典型RC框架结构建模并进行基于IDA方法的地震易损性分析,得出如下结论:
(1)严格按照我国现行规范设计的RC框架结构,一般都能达到“大震不倒”的抗震设防目标。
(2)随着框架柱轴压比的增大,相同地震动强度下结构越容易发生轻微破坏和严重破坏,结构抗倒塌能力减弱,且框架结构在地震作用下不易形成“强柱弱梁”破坏机制。该结论诠释了汶川地震震害中RC框架结构多数塑性铰首先出现在柱端,结构最终破坏形式为“强梁弱柱”的现象。
(3)房屋的高宽比对RC框架结构抗震性能的影响不显著。究其原因,由于设计的RC框架结构都是严格按我国现行规范设计计算,随着高宽比的增大,框架柱截面尺寸也不同程度地增大,使得结构抗倒塌能力相应增强,一定程度上抵消了高宽比增大对抗震性能带来的不利影响。
(4)随着混凝土强度增大,相同地震动强度下RC框架发生轻微破坏和严重破坏的概率越小,且框架结构的抗倒塌能力增强。
(5)随着框架梁柱纵筋强度的提高(如采用HRB500钢筋),相同地震动强度下结构较容易发生轻微破坏和严重破坏,但结构抗倒塌的能力相应增强。
References)
[1]王亚勇,高孟潭,叶列平,等.基于大震和特大震下倒塌率目标的建筑抗震设计方法研究方案[C]//第八届全国地震工程学术会议论文集:Ⅱ.重庆:重庆大学,2010.
WANG Ya-yong,GAO Meng-tan,YE Lie-ping,et al.Study on Design Method of Building Seismic Design Based on Collapse Rate under Rare and very Rare Ground Motion[C]//Proceedings of 8thNational Earthquake Engineering Conference:Ⅱ.Chongqing:Chongqing University,2010.(in Chinese)
[2]李文博.基于IDA方法的RC框架结构地震易损性分析研究[D].西安:西安建筑科技大学,2012.
LI Wen-bo.Study on Seismic Fragility Analysis of RC Frame Structures Based on the IDA Method[D].Xi'an:Xian University of Architecture and Technology,2012.(in Chinese)
[3]GB 50010-2010,混凝土结构设计规范[S].北京:中国建筑工业出版社,2010.
GB 50010-2010,Code for Design of Concrete Structures[S].Beijing:China Architecture & Building Press,2010.(in Chinese)
[4]Spacone E,Filippou F C,Taucer Fiber F F.Beam-column Model for Nonlinear Analysis of R/C Frames:Part 1.Formulation[J].Earthquake Engineering and Structural Dynamics,1996,25 (7):711-725
[5]Applied Technology Council,Federal Emergency Management Argency.Quantification of Building Seismic Performance Factors[R].America:FEMA,2008.
[6]FEMA 356,Prestandard and Commentary for the Seismic Rehabilitation of Builings[S].Washington D C,2000.
[7]龚思礼.建筑抗震设计手册[M].第二版.北京:中国建筑工业出版社,2003.
GONG Si-li.Handbook for Seismic Design of Buildings[M].Second Edition.Beijing:China Architecture and Building Press,2003.(in Chinese)
[8]梁兴文,史庆轩.混凝土结构设计原理[M].北京:中国建筑工业出版社,2008.
LIANG Xing-wen,SHI Qing-xuan.Design Principle of Concrete Structures[M].Beijing:China Architecture and Building Press,2008.(in Chinese)
[9]杨志利.钢筋混凝土框架结构“强柱弱梁”屈服机制影响因素的研究[D].青岛:青岛理工大学 2010.
YANG Zhi-li.Research on Affecting Factors of Strong Column Weak Beam Yield Mechanism of Reiforced Concrete Frame Structures[D].Qingdao:Qingdao Technological University 2010.(in Chinese)
[10]赵亮.配置不同强度等级钢筋的混凝土框架结构非线性动力反应分析[D].重庆:重庆大学,2009.
ZHAO Liang.Nonlinear Dynamic Response Analysis of Concrete Frame Structures with Steel Bars of Different Strength[D].Chongqing:Chongqing University,2009.(in Chinese)
Influence of Design Factors on Seismic Fragility of RC Frame Structures
ZHENG Jie,ZUO He-shan,LI Wen-bo,LEI Zhen-dong,ZHENG Shan-suo
(Architectural Design Institute,Xi'an University of Architecture and Technology,Xi'an 710055,Shaanxi,China)
The seismic resistance of structures involves uncertainty regarding the structure and the earthquake,and is coupled with non-linear variables.This paper employs Incremental Dynamic Analysis (IDA)to analyze the earthquake uncertainties.Based on OpenSEES finite element modeling theory,16 ground motion records were selected.After a discussion on the seismic vulnerability of 13 plane frame structures,this paper clarifies the influence of 4 parameters on the seismic resistance levels that RC frame structures can attain.These parameters are axial compression ratio,height-width ratio,concrete strength,and longitudinal reinforcement strength.The results show that RC frame constructions,which are designed in strict accordance with current specifications,can meet the target of "no collapse in a large earthquake"; the influence of the height-width ratio on seismic resistance is not obvious; on the premise of similar axial compression ratios,increase in concrete strength can improve the seismic resistance of structures.Under the same earthquake,for structures with high beam-column longitudinal reinforcement strength,the probability of reaching the immediate occupancy and life safe states is larger than that of structures with low beam-column longitudinal reinforcement strength,but the latter show better collapse resistance.
RC frame structure; axial compression ratio; seismic fragility; collapse resistant capacity
2015-07-22
国家科技支撑计划(2013BAJ08B03);教育部高等学校博士学科点专项科研基金(20136120110003)
郑捷(1988-),女,陕西西安人,硕士,从事建筑与结构设计研究。E-mail:julie1314fl@126.com。
TU375
A
1000-0844(2016)04-0491-07
10.3969/j.issn.1000-0844.2016.04.0491

