雷达资料和网格法在城市内涝系统中的应用

李恒升，高玉春，陈德生

（1.成都信息工程学院 四川 成都 610225；2.中国气象局气象探测中心 北京　100081；3.河南省气象局 河南 郑州　450003）

雷达资料和网格法在城市内涝系统中的应用

李恒升1，高玉春2，陈德生3

（1.成都信息工程学院 四川 成都 610225；2.中国气象局气象探测中心 北京100081；3.河南省气象局 河南 郑州450003）

多普勒天气雷达是监测暴雨等灾害性天气的重要手段。文中将郑州雷达站某次降雨的雷达1小时累积雨量（OHP）产品资料通过网格插值法处理成内涝数学模型所需的降雨数据，再将其带入内涝系统中，进行郑州市区内涝积水的模拟。同时，通过调整网格插值法中的相应参数使模型的计算值与实测值之间的误差不断减小，以更接近实际情况。结果分析表明，网格间距d和搜索半径R都较小时，计算值较接近于实测值。

雷达OHP产品；网格插值法；内涝数学模型；内涝系统

城市内涝灾害对城市造成的严重经济损失，早已引起了世界各国对城市内涝问题的普遍关注，很多国家都展开了程度不同的相关研究。发达国家城市化现象出现较早、对城市水涝灾害风险特性和演变规律、城市水涝灾害综合防治对策研究起步较早，已取得可借鉴的成果［1］。

从八十年代到现在，我国城市内涝灾害加剧的现象特别突出。为此我国水利方面的专家和学者对城市内涝进行了相应的探索和实验。将内涝数值模拟方法用于城市内涝的研究，在我国虽然起步比较晚，但发展迅速［2］。我国最早研制的城市内涝仿真模型已具备了一定的模拟城市内涝的能力。随后，天津气象科研所与中国水利水电科学研究院减灾中心合作，在原有的城市内涝仿真模型的基础上，研制了天津市城区内涝仿真模型［3］。南京、南昌、太原、西安、郑州等省会城市近年来也先后开展这方面的研究，取得了一些初步成果。

所谓的城市内涝是指由于城市强降水或 连续性降水，使得城市内总的降雨量超出了城市排水能力而使城市内产生积水灾害的现象。2010年，针对国内351个城市在2008年至2010年间的内涝情况，住建部专门做了一项调查，该调查显示：发生过不同程度内涝的城市有62%，其中有137个城市发生过超过3次以上的内涝灾害。因此，研究城市强降水内涝系统的实际意义是为了将灾害程度降低到最小，从而保证人民群众的生命财产不受损失。

文中利用网格插值法将雷达1小时累积雨量 （OHP）产品资料转化为降雨边界条件，然后将该条件带入内涝数学模型中，得到相应的积水数据。同时，通过调整网格插值法中的参数，使模拟的积水数据更接近于实际情况。

1　内涝系统

1.1城市强降水内涝系统

强降水内涝系统包括3大块：模型前处理、模型计算和模型后处理。本文要完成的是模型前处理中的图形显示与编辑和雨量信息转化、计算结果的显示和相关数据处理。本文主程序的大概流程：数据采集—面雨量计算—积水模拟—结果显示。

1.2城市内涝数学模型的利用

城市内涝数学模型以平面二维非恒定流的基本方程和无结构不规划网格划分技术为骨架，结合一维非恒定流方程的算法，以FORTRAN语言编写的程序为载体，计算得出网格积水深度、最大积水深度、水流速度等结果。

建立适合内涝数学模型程序所需的降雨边界条件是本文计算郑州市积水深度的关键，首先，要获得模型所需的初始数据，如不规则网格数据和初始水深等相关参数；其次，通过时间积分方法将每个体扫更新一次的1小时累积雨量资料处理成6分钟累积雨量资料，再通过网格插值算法得到各不规则网格的面雨量数据作为降雨边界条件；最后，配合时间参数将以上数据输入内涝数学模型程序得到积水深度信息，同时在ArcGIS9.3上显示城区积水深度，并通过对计算结果和实测结果的对比分析选出一组较适合的参数应用在郑州市内涝系统中。

2　数据资料处理

2.1无结构不规则网格划分

由于内涝数据模型采用的是有限元体积法的思想，利用无结构不规则网格作为模型的计算单元，因此需要根据郑州市地形、地物特点及网格划分原则，对郑州市三环以内城区（主要内涝集中区）的地形地物进行概化。本文直接使用郑州市气象局提供的网格划分数据。该数据的划分是根据郑州市的地势及内涝特点，把河流作为二级河道，把市区内的帝湖看作湖泊型网格，对公园和绿地的糙率度赋值为0.065。在进行网格划分时充分考虑地形地貌特征，网格内的下垫面属性尽可能的相同，设计网格时根据实际积水区的大小调整网格的疏密［4］。最后生成无结构不规则网格数 1080个，通道数2405个及节点数1326个。

2.2降雨数据采集

雷达估测降雨是根据多普勒天气雷达测雨的优势，能够在恶劣的气候条件下提供可靠的降雨数据。本文利用多普勒天气雷达1小时累积雨量（OHP）产品作为降雨数据，但该数据并不是模型所需的直接降雨数据，需要经过时间积分及插值处理。所谓的OHP产品是指到当前体扫为止1小时连续累积的总雨量，每个体扫更新一次。相邻OHP产品间的时间间隔实际上是5或6分钟，但并不是从整点开始间隔5或6分钟生成一次产品。

因为内涝数学模型程序所需的文件中每个雨量点信息是以0.1小时为时间间隔的各时次雨量信息，即从整点开始每间隔6分钟的各累积雨量信息，而一般OHP产品生成的时间并不与之对应，所以需要将已生成的多个连续的OHP产品数据处理成从整点开始每间隔6分钟的各累积雨量数据。本文先将每个体扫生成的1小时累积雨量换算为该小时内的平均雨强，作为从前一体扫结束时刻到当前体扫结束时刻这一时间段内的雨强值。然后，以时间为X轴，雨强值为Y轴建立二维坐标系，将各个时段内对应的函数表示为y=“对应的雨强值”×t（左连续），从而构成了一个阶梯函数。最后，通过积分求出从整点开始每间隔6分钟的各累积雨量数据。

由于雷达OHP产品反映的是以雷达站为中心，230 km范围内的累积雨量情况，而所研究区域在距离雷达20 km范围以内，因此，本文先将不规则网格节点及其经纬度坐标信息输入到ArcGIS9.3中，然后在ArcGIS9.3上选取研究区域及其以外两公里范围内的雷达雨量点信息，并将这些数据转化为后续程序所需的数据。

2.3网格插值法

有限的雨量点资料总是难以完全反映降雨在整个区域的空间分布特性，研究降雨空间变异离不开空间插值，空间插值是分布式水文模型的关键技术和难点之一［5］。本文利用网格插值法将点雨量数据转换为面雨量数据，作为降雨边界条件。

网格插值法的基本思路：先将郑州市三环以内城区网格化，使网格覆盖在该区域面上，并通过网格插值法进行相关运算处理，计算出各网格结点上的雨量值。本文利用网格插值法的步骤（如下）：

1）确定直角坐标系原点，建立坐标系，使郑州市三环以内城区在第一象限内，建立m×n的正方形网格面（网格间距d可选），并使该网格面略大于该研究区域。

2）选定搜索半径R，计算出以某个网格点为圆心，R为半径圆内的雷达雨量点数，用经典距离倒数平方法（如公式（1）和（2）所示，令（2）式中b=2）计算该网格点的雨量。

权重系数：

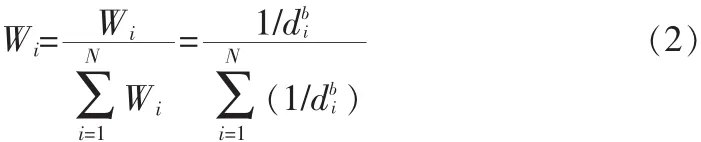
式中：Pk为任意网格点的降雨量；Pi为第i个参考雨量点的降雨量；N为确定第k个网格点降雨量所用参考雨量点的个数；Wi为各参考雨量点对于第k个网格点的权重；wi为参加第k个网格点计算的参考雨量点的权重系数；d为参考雨量点到网格点的距离；b为权重指数。

3）计算每个网格的平均面降雨量，将网格4个顶点的点雨量值直接进行算数平均求出该网格的面平均雨量值。然后，将网格的面平均雨量转换为各无结构不规则网格的面雨量。最后，处理成内涝数学模型所需的降雨文件。

3　结果数据显示与分析

3.1积水模拟显示

首先，将模型所需的降雨文件，带入到内涝数学模型中，便可得到相应的积水深度等相关结果数据文件。然后，通过程序处理成显示所需格式的数据文件。

本文积水模拟显示功能不仅可以显示最大积水，还可以直观地显示计算过程中积水深度及对应时刻面雨量的动态变化。图1是2014年6月19日郑州市强降雨的积水模拟显示结果。

图1　2014年6月19日　郑州积水模拟显示结果Fig.1　hengzhou seeper simulation shows the result

3.2结果数据分析

由强降水所造成的内涝灾害，通常可以用最大积水深度来衡量。城市内涝系统的验证的方法，就是选择不同的强降水个例做为降雨边界条件，代入系统中进行计算［6-7］。通过对误差的分析，修正相关参数，改进计算方法，使计算值与实测值之间的误差不断减小。

本文选择2014年6月19日郑州市强降雨数据作为一个降雨个例，然后处理成模型所需的降雨边界条件。由于事先不能确定什么样的d和R能使计算结果和实测结果的误差达到最小，因此，需要通过大量数据分析来找到较优的d 和R。本文分别使d取值 20个（0.25、0.5、…4.75、5）和R取值14个（1.5、2、…7.5、8）（单位全部为km）组成280组参数对，再分别将这280组参数代入内涝系统中进行计算。然后通过对模型的计算结果和实测结果的分析比较，找出较好的参数组。最后，将选出的参数组作为本内涝系统的固定参数。

通过对每个积水点在280组参数下的统计分析，可以看出大部分积水点在所有参数组下的变化规律是相似的。本文选取某个积水点的统计图来做一下分析说明，但不能认为单从某个积水点中找到最接近实测值的那组参数就可以了，因为同一参数组下每个积水点的计算值与实测值的接近程度是一样的，需要找到比较稳定的参数组，才能更可靠的反映实际情况。

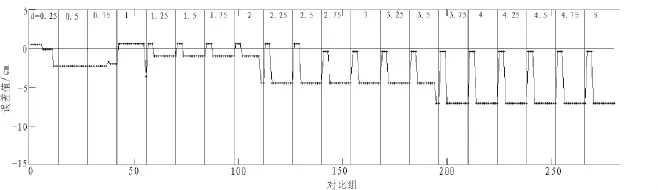
图2　不同网格间距（d）的积水点误差值随搜索半径（R）的变化情况Fig.2　The water point error value of different grid spacing（d）change with the search radius（R）

1）如图2、3所示（图中，相邻d间用竖线隔开，每个d下对应14个搜索半径R；黑点代表某组参数下的误差值或相对误差值）。从图2可以看出，当d大于等于1后，无论d怎么增大，R为1.5、2和2.5时对应的误差值始终比其他R值更接近0。而且，有图3中对应的相对误差可以看出，对应的相对误差要小于其他R值下。

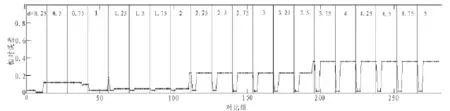
图3　不同网格间距（d）的积水点相对误差值随搜索半径（R）的变化情况Fig.3　The water point relative error of different grid spacing（d）change with the search radius（R）

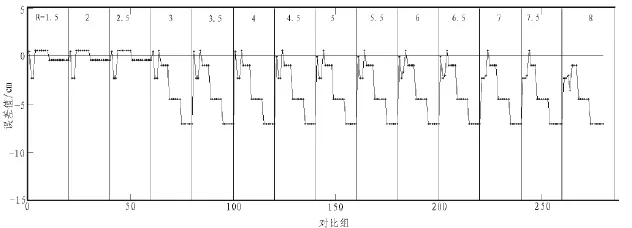
图4　不同搜索半径（R）的积水点误差值随网格间距（d）的变化情况Fig.4　he water point error value of different search radius（R）change with the grid spacing（d）

图5　不同搜索半径（R）的积水点相对误差值随网格间距（d）的变化情况Fig.5　he water point relative error of different search radius（R）change with the grid spacing（d）

2）如图4、5所示（图中，相邻R间用竖线隔开，每个R下对应20个网格间距d）。从图4可以看出，当R小于等于6.5，d为0.25和1时对应的误差值始终比其他d值更接近0。而且，有图5中对应的相对误差可以看出，对应的可信程度要大于其他d值下的。

综上所述，网格间距d可取0.25或1，搜索半径R可取1.5、2或2.5。在选取满足以上两个条件的参数组下，计算结果更接近于实测结果且可信程度高。

4　结　论

文中所研究的区域是郑州市三环以内城区，在14km×14km范围之内。利用雷达OHP产品数据将网格插值法应用于郑州市内涝系统中，通过对结果数据的分析得出以下结论：

1）由于雷达OHP产品的分辨率是2 km，因此搜索半径R不能过大。同一网格间距d下当R过大时，计算值将明显偏离实际值。

2）由于所研究区域最大范围是14 km×14 km，因此，d也不能过大。当d大于最大边长的1/3时，计算值严重偏离实际值。

3）当R和d取较小值时，计算值更接近于实际值。但从另一方面来说，d越小，网格点数就越多，反而会增加计算的时间，因此d取1比取0.25更合适。

由于降雨数据由气象部门提供，比较容易得到，但实测的积水数据比较难得到，从而造成本文在分析数据时利用的个例较少，因此，不能更全面的反映实际积水情况。如果能有较新的郑州市地理信息和管网等相关数据，并能得到更多的个例数据进行数据分析，那么会比本文更好的反映郑州市的实际积水情况。

［1］杨东.基于GIS的成都城市暴雨内涝预报预警系统研究开发［D］.成都：电子科技大学，2010.

［2］陈波.武汉城市强降水内涝仿真模拟系统研究 ［D］.南京：南京信息工程大学，2007.

［3］LI Da-ming，ZHANG Hong-ping，LI Bing-fei，et al.Basic Theory and Vlathmatical Modeling of Urban Rainstorm Water Logging［J］.Journal of Hydramechenics，Ser.B，2004，16 （1）：17-27.

［4］彭记永，孙岩，张晓娟，等.郑州城市暴雨灾害仿真系统研究及应用［J］.安徽农业科学，2010，38（11）：5736-5738.

［5］杜迎燕.基于网格的面雨量实时计算方法研究［D］.南京：河海大学，2006.

［6］解以扬，李大鸣，李培彦，等.城市暴雨内涝数学模型的研究与应用［J］.水科学进展，2005，16（3）：384-390.

［7］景学义，刘宇飞，王永波，等.哈尔滨市城市内涝监测预警系统建设［J］.灾害学，2009，24（1）：54-57.

Radar data and grid method in the application of urban waterlogging system

LI Heng-sheng1，GAO Yu-chun2，CHEN De-sheng3
（1.Chengdu University of Information Technology，Chengdu 610225，China；2.CMA Meteorological Observation Center，Beijing 100081，China；3.Henan Meteorologicial bureau，Zhengzhou 450003，China）

Doppler radar is an important tool for monitoring the storm and other severe weather.In this paper，1-Hour Precipitation Accumulation products of a single rainfall in Zhengzhou radar station is processed by grid interpolation into a rainfall data the waterlogging mathematical models is needed to，and then the rainfall data is brought into waterlogging system to simulate Zhengzhou city waterlogging water accumulation.At the same time，it adjusts the corresponding parameters in grid interpolation to make the error between the calculated and measured values decreasing，to be closer to the actual situation.The resultsshow thatwhenthegridspacingdandsearchradiusR aresmall，thecalculated valueisclosertothemeasuredvalues.

radar OHP products；grid interpolation method；waterlogging mathematical model；waterlogging system

TN595.4

A

1674－6236（2016）03-0125-04

2015-03-24稿件编号：201503326

李恒升（1989—），男，河南南阳人，硕士研究生。研究方向：气象雷达系统及信号处理。