颈部材料对亥姆霍兹共振器吸声性能的影响

陈　明，李　鹏，罗　斌

（1.贵州工业职业技术学院，贵州　贵阳　550001；2.东南大学微电子机械系统教育部重点实验室，江苏 南京 210096）

颈部材料对亥姆霍兹共振器吸声性能的影响

陈明1，2，李鹏2，罗斌2

（1.贵州工业职业技术学院，贵州贵阳550001；2.东南大学微电子机械系统教育部重点实验室，江苏 南京 210096）

为改善亥姆霍兹共振器的吸声系数和吸声带宽，采用不同参数的穿孔材料优化共振器吸声效果。鉴于多孔传声过程较为复杂，利用平行穿孔板对声阻抗进行研究，建立颈部入口声阻抗计算模型。搭建管道声学实验台，在声学管道上游布置扬声器，在管道下游布置亥姆霍兹共振器。测量不同颈部材料下的静流阻率和吸声系数，计算共振器颈部入口声阻抗。研究表明：颈部材料中的管流效应不可忽略，穿孔率对静流阻率的影响很大，平均流速相同时，孔径越大，静流阻率越小；大孔径穿孔板具有明显优势，因此设计亥姆霍兹共振器时穿孔板孔径应大于4mm。

亥姆霍兹；共振器；穿孔板；颈部材料；吸声

0　引言

亥姆霍兹共振器结构简单且吸声性能良好，被广泛应用于吸声降噪系统中，经典的亥姆霍兹共振器由颈部和空腔两部分构成［1］。但是亥姆霍兹共振器的吸声频段较窄，吸声性能优化一直是学者们研究的重要课题［2］。Matsuhisa等通过改变空腔体积调节共振器吸声频率；Zhao等通过研究长径比优化共振器的吸声性能；Ingard研究了颈部形状、直径、位置对共振频率的影响，并提出了颈部和共振腔的修正因子［3-4］。由于空间有限，改变空腔体积似乎可行性较低，优化共振器颈部结构更为可行。Chanaud在Ingard的基础上，对圆柱形谐振腔孔径和腔体进行了端部修正，得出谐振腔体积和开孔面积一定时，穿孔位置对共振频率的影响较大［5］。由国内外研究进展可知，若颈部延伸至共振器内部，可以在不增加共振器体积的前提下降低共振频率。改变共振器颈部长度、形状或者在颈部延长段布置穿孔板均可改变共振频率，因此本文在颈部添加平行穿孔的陶瓷材料，通过改变颈部材料的孔径、穿孔率等参数调节入口声阻抗。亥姆霍兹共振器在共振频率附近的声抗为0，此时的颈部速度脉动幅值最大，非线性效应显著。为了准确计算共振器入口声阻抗，建立了亥姆霍兹共振器颈部入口声阻抗计算模型，通过搭建管道声学实验台，计算了共振器颈部入口声阻抗，测量了不同颈部材料的静流阻率和吸声系数，以期为今后的相关研究提供参考。

1　共振器声阻抗模型

1.1单孔阻尼模型

为了研究颈部材料对吸声性能的影响，首先应建立入口声阻抗计算模型。鉴于多孔传声过程较为复杂，本文利用平行穿孔板对声阻抗进行研究，假设穿孔板上为均匀分布的圆孔，建立单孔阻尼模型，求解共振器入口声阻抗［6］。由于亥姆霍兹共振器颈部为平行穿孔板，声压传播到共振器空腔时需要通过圆孔，因此可将穿孔板看作平行传声管道，如图1所示。

图1　管道传声模型

在Re＜3 000时，管道内为层流，管内压力分布可用线性模型计算。忽略热传导效应，建立柱坐标系下的动量方程：

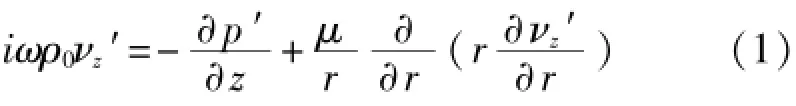
式中：ρ0——空气密度；

p′——压力脉动值；

μ——粘性系数；

ν′——速度脉动值。

式中：s——r与粘性边界层厚度比；

J0、J1——0阶、1阶贝塞尔函数。

在Re＞10000时，管道内部为湍流，ν′增大，此时应采用非线性静流阻对声波传播进行研究。根据Wilson试验，此时的管道轴向压力梯度为

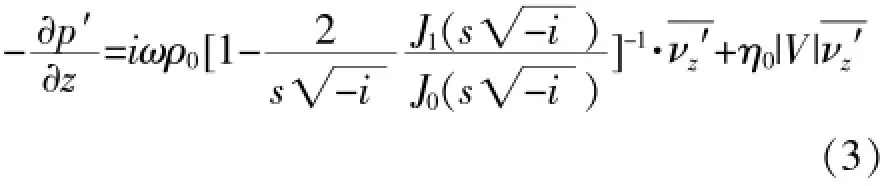
式中：η0——静态非线性福熙海麦系数；

V——管道内质点速度。

典型亥姆霍兹共振器的颈部空气脉动速度不会太大，因此很少考虑非线性静流阻［7］。但是共振器在共振频率附近工作时，颈部雷诺数会很大，此时应该考虑非线性效应［8］。如果颈部长径比较小，则非线性效应不可忽略，本文设计的穿孔板孔径在1.5～14mm，材料厚度为25 mm，经计算共振频率下的脉动速度幅值对应的雷诺数为100～1000，湍流可以忽略，可用线性模型计算。但如果管道内声速较大时，非线性效应不可忽略，需要研究静态流阻率对声阻抗和吸声系数的影响。

1.2颈部入口模型

由于共振器颈部长度远小于声波波长，假设颈部空气在压力差的作用下做整体脉动，在轴向上无相位差，如图2所示。

图中颈部左右的压力差为

式中：l′——颈部有效长度；

Gc（s）——声压扰动幅值。

图2　颈部安装穿孔板的亥姆霍兹共振

为获得颈部入口处的声阻抗，认为空腔内的声波为一维谐波，其压力和速度表达式为

式中c为当地声速。

共振器颈部体积流量和压力均连续，因此共振器颈部声阻抗也为连续，由此可知：

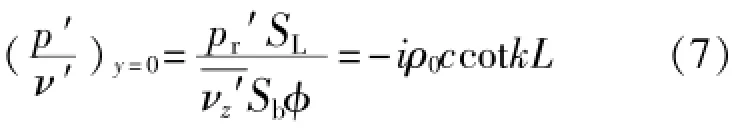
将式（7）带入式（2），得出共振器入口声阻抗为

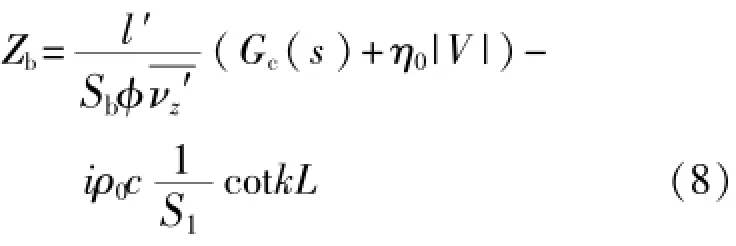
式中：l′——材料厚度；

Sb——颈部截面积；

k——非充分发展系数；

L——空腔长度。

由于粘性边界层的厚度远小于穿孔板直径，谐振腔尺寸也远小于声波波长，因此颈部入口处的声阻抗可以表示为

式中：ω——共振角频率；

φ——穿孔率。

当频率偏离共振频率时，声抗远大于声阻，速度脉动量较小。当频率接近共振频率时，声阻明显增大，此时非线性作用显著。

2　吸声性能实验研究

2.1静流阻率测量

为了研究共振器颈部入口非线性声阻抗，需要测量颈部材料的静流阻率［9］。本文在研究中共设计了6种试验材料样品，见表1。

样品1～样品3用于测量静流阻率；样品1、样品4、样品5、样品6用于测量吸声系数。实验选择的穿孔板厚度均为25mm，穿孔率十分接近，因此共振器的共振频率相近。利用经典声学理论计算不同流速下的静流阻率，如图3所示。利用静流阻率实验台对样品1～样品3的静流阻率进行测量，试验结果见图4。

表1　不同参数的颈部材料

图3　不同流速下的静流阻率理论值

图4　不同流速下的静流阻率实验值

对比图3、图4可知，实验测量值比理论计算值偏大，且流速越大二者偏离值越大。当流速趋近于0cm/s时，理论值与实验值相等。流速越大，静流阻率非线性越显著，这与上一章的分析相吻合。样品1的静流阻率明显大于样品2和样品3，说明穿孔率对静流阻率的影响很大。对比样品2和样品3，平均流速相同时，孔径越大，静流阻率越小，此时管内流动处于非充分发展阶段。

2.2吸声系数测量

为了测量不同颈部材料亥姆霍兹共振器的吸声系数，搭建了管道声学实验台，在声学管道上游布置扬声器，在管道下游布置亥姆霍兹共振器。通过控制计算机发出简谐电压信号，经扬声器后转化为单频声波，通过计算共振器上下游声场分布，得出吸声系数。为了保持实验具有对比性，取共振器入口声压为120dB。

由于穿孔率＜1，加装穿孔板后，减小了颈部有效面积，因此共振器的频率会比加装穿孔板前有所降低。通过测量发现，在频率为150，290，410Hz时，共振器的吸声系数发生突降，反射声波与入射声波相互抵消，此时共振器的入口声压为0，吸声系数也接近0。为了研究颈部材料对吸声系数的影响，取样品1、样品4、样品5、样品6为试验材料，测量共振频率在205Hz和370Hz的吸声系数，试验结果见图5（a）和图5（b）。

由图可知，不同颈部材料的吸声系数曲线有一定差别，特别是在共振频率为370Hz时，样品1和样品6的吸声系数明显小于样品4和样品5，这主要是穿孔率和孔径不同导致的。样品1和样品6的孔径小于样品4和样品5，孔径小导致吸声带宽越大，但并不能简单地认为小孔径较大孔径好。当孔径较小时，随着孔径的进一步下降，共振频率对应的吸声系数下降得很快，图5（b）中样品4和样品5的共振吸声系数基本相同，但是样品6的共振吸声系数明显小于样品4，样品5的孔径为8mm，样品4为4mm，样品6为2.5mm，由此说明共振吸声系数在2.5～4mm内下降较快，建议孔板孔径＞4mm。根据实验结果：两种共振频率下，大孔径穿孔板具有明显优势，因此设计亥姆霍兹共振器时穿孔板孔径应大于4mm。

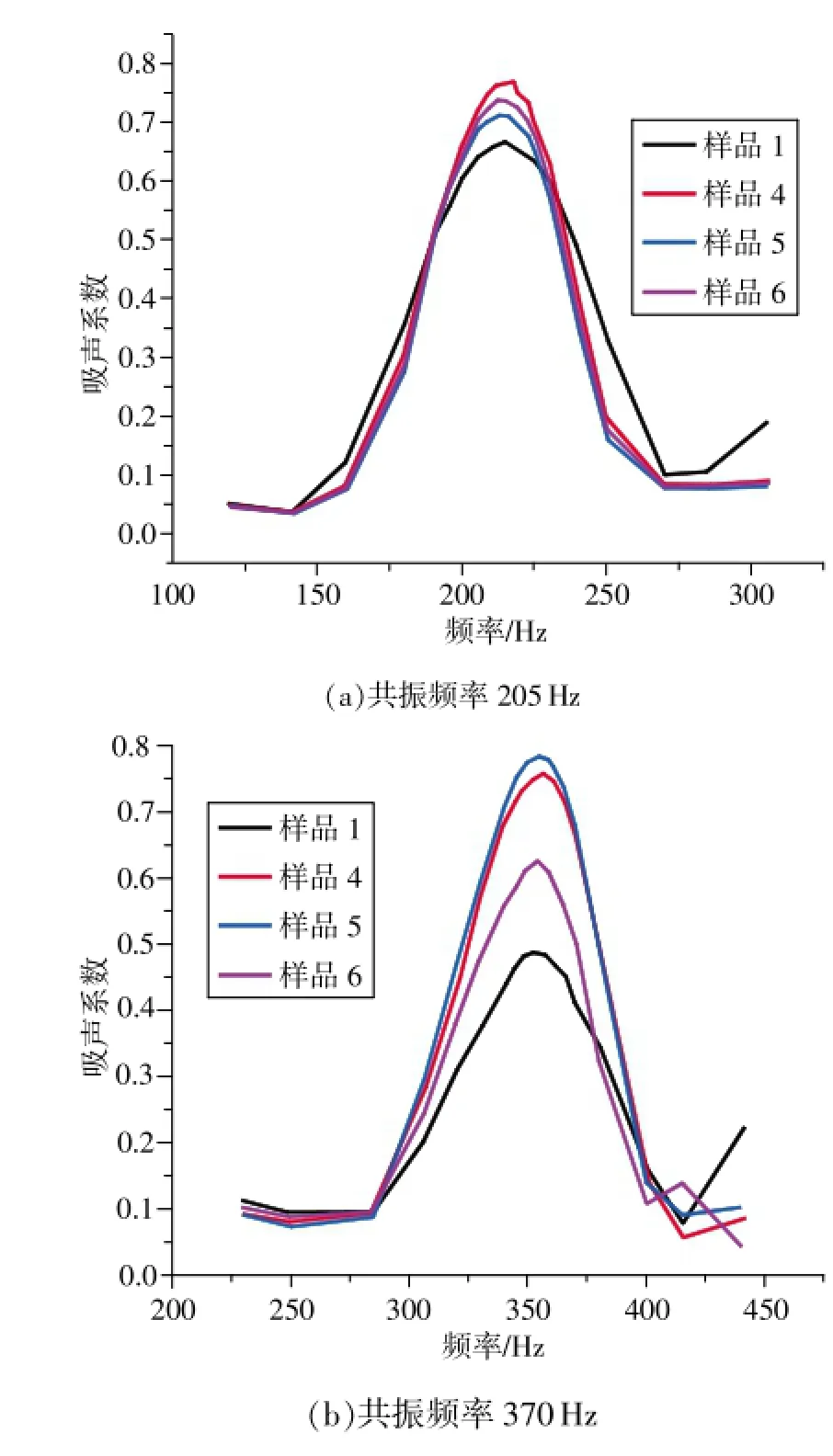
图5　 不同共振频率下的吸声系数

3　结束语

穿孔直径和穿孔材料对亥姆霍兹共振器颈部入口声阻抗具有重要影响，可改善共振器的吸声系数和吸声带宽。亥姆霍兹共振器在共振频率附近的声抗为0，此时的颈部速度脉动幅值最大，非线性效应显著。为了准确计算共振器入口声阻抗，建立了亥姆霍兹共振器颈部入口声阻抗计算模型，计算了共振器静流阻率，并重点测量了不同颈部材料的静流阻率和吸声系数，研究表明：颈部材料中的管流效应不可忽略，穿孔率对静流阻率的影响很大，平均流速相同时，孔径越大，静流阻率越小；大孔径穿孔板具有明显优势，亥姆霍兹共振器穿孔板孔径应大于4mm。

［1］韩旭，李波，李昭，等.基于亥姆霍兹共鸣器的声电转换系统研究［J］.压电与声光，2014，36（6）：925-928.

［2］李华，任坤，殷振，等.纵弯转换超声振动球面聚焦系统聚焦特性研究［J］.压电与声光，2014，36（3）：450-454.

［3］MATSUHISAH，RENB.Semiactive control of duct noise by a volume-variable resonator［J］.JSME International Journal，1992，35（2）：223-228.

［4］ZHAODA，BARROWC，MORGANS A S，et al. Acousticdampingofahelmholtzresonatorwithan oscillating volume［J］.AIAA Journal，2009，47（7）：1672-1679.

［5］CHANAUD R C.Effects of geometry on the resonance frequency of Helmholtz resonators，part II［J］.Journal of Sound and Vibration，1997，204（5）：829-834.

［6］王泽锋，胡永明，熊水东，等.腔壁弹性对水下小型圆柱形亥姆霍兹共振器共振频率的影响［J］.物理学报，2009，58 （4）：2507-2512.

［7］盖晓玲，李贤徽，杨军，等.吸声材料对亥姆霍兹共振器吸声性能的影响［J］.电声技术，2012，36（11）：1-4.

［8］靳国永，张洪田，李玩幽，等.基于可调频亥姆霍兹共振器的封闭空间噪声自适应半主动控制［J］.声学学报，2010，35（3）：309-320.

［9］陈怀军，赵文霞，郝长春.亥姆霍兹共振器孔径长度对声学超构材料性能的影响［J］.西安文理学院学报（自然科学版），2015，18（3）：55-57.

（编辑：李妮）

Neck materials influence to Helmholtz resonator sound absorption performance

CHEN Ming1，2，LI Peng2，LUO Bin2
（1.Guizhou Industry Polytechnic College，Guiyang 550001，China；2.Key Lab of MEMS of Education Ministry，Southeast University，Nanjing 210096，China）

To improve Helmholtz resonators'acoustic absorptivity and sound absorption bandwidth，soundabsorptionmaterialswithdifferentparameterswereusedtooptimizeresonatorsound absorptioneffect.Inviewoftheporoussoundtransmissionprocesscomplicated， parallel perforations were usedinacoustic impedancestudy.The Helmholtz resonatorneckentrance acoustic impedance calculation model has been established.The duct acoustic test bench was built，whichinstalledspeakerupstreamandHelmholtzresonatordownstream.Variousneck materials'static resistivity and absorption coefficient were measured.And the acoustic impedance of resonator neck entrance was calculated.Research shows that：neck materials'tube flow effect cannot be neglected；perforation rate has a great influence on static resistivity；when average flow velocity was equal，the larger aperture，the smaller static resistivity；perforation plate with large aperture has obvious advantages，Helmholtz resonator perforation plate diameter should be greater than 4 mm.

Helmholtz；resonator；perforation plate；neck materials；sound absorption

A

1674-5124（2016）08-0127-04

10.11857/j.issn.1674-5124.2016.08.026

2015-11-15；

2016-01-05

国家自然科学基金项目（51577029）

中央高校基本业务科研专项经费资助项目（2013XS038）

陈明（1979-），男，贵州印江县人，讲师，研究方向为电子科学与技术。