基于和声搜索算法的配电网无功优化

朱庆钢，张　波，郭　翔，张金良，娄婷婷

（1.国网山东省电力公司潍坊供电公司，山东　潍坊　261021；2.国网山东省电力公司济南供电公司，济南　250012；3.国网山东省电力公司电力科学研究院，济南　250003）

基于和声搜索算法的配电网无功优化

朱庆钢1，张波1，郭翔2，张金良1，娄婷婷3

（1.国网山东省电力公司潍坊供电公司，山东潍坊261021；2.国网山东省电力公司济南供电公司，济南250012；3.国网山东省电力公司电力科学研究院，济南250003）

将一种新型人工智能算法即和声搜索算法（HSA）应用于配电网无功优化中，建立以网损最小为目标函数的无功优化数学模型。考虑配电网运行电压指标要求，合理设置补偿范围，实现了同时求解补偿位置与补偿容量。该算法通过和声保留、音调调节和随机选择3种方式更新和声解向量，保持和声多样性，避免出现收敛早熟，提高算法收敛稳定性。用IEEE-33节点与美国PG&E69节点系统进行仿真计算，其仿真结果与PSO算法对比表明，HSA在收敛稳定性、计算精度等方面具有一定优势，进而论证了HSA用于配电网无功优化的可行性与有效性。

配电网；无功优化；和声搜索算法（HSA）；和声保留；音调调节

0　引言

近年来，我国电力工业迅速发展，电力系统的运行经济性日趋突出和重要。配电网络作为从电力系统到用户的最后一个环节，与用户之间联系十分紧密，直接影响到用户的供电可靠性与供电质量。目前，我国配网普遍存在电压合格率低、网络损耗大等现象。怎样在满足电力系统负荷要求及系统约束条件下降低配网的网络损耗，提高供电可靠率及用户电能质量，使电力系统保持安全稳定经济运行，是电力系统迫切需要解决的问题，而研究配网无功优化是解决此问题的关键。

配电网中调节变压器变比对系统的无功功率影响很小，因此配电网主要是投切并联补偿电容器实现配电网的无功优化控制。由于输电网主要是集中补偿方式，其无功功率补偿设备一般设置在变电站内，所以输电网的电压无功优化就是指变电站电压无功优化。而配电网主要有分散补偿、就地补偿以及二者结合的方式，所以配电网无功优化的内容是投切配电网中不同位置的无功功率补偿装置，合理调整配电网中的无功功率，使配电网网损降低。配网无功优化主要是指在确保配网安全稳定可靠运行的条件下，在系统等值网络中加设配网无功补偿装置来有效调整配网系统中存在的电压与功率分布，从而使系统中网损达到最小，进一步提高电压质量［1］。此外，由于配电网无功优化的重要性，很多研究人员对无功优化进行了相关研究，提出了诸多算法与思想。其中大致可以分为传统型优化算法与人工智能算法两种。传统型优化算法［2-4］主要包括混合整数规划法、线性规划法、非线性规划法等。但是随着现代电力系统规模日益增大，其解空间是复杂多维的，因此传统型优化算法难以处理离散变量，易陷入局部最优解而非全局最优。人工智能算法主要包括遗传算法、禁忌算法、粒子群算法等。文献［5］介绍了传统遗传算法在配电网无功优化中的应用，但是在实际应用研究中，传统的遗传算法采用的交叉率和变异率固定不变不利于全局最优。粒子群算法［6］应用于高维复杂优化问题时，易发生过早收敛以及陷入局部最优中粒子群趋向同一，并且粒子间存在多样性，导致该算法在进化迭代后期收敛速度缓慢，陷入局部最优。禁忌算法寻优速度较快，但是该算法收敛会受初始值影响，并且算法搜索效率与最终结果会受到禁忌表的期望水平与深度影响［7-8］。

提出一种新的基于和声搜索的人工智能算法（Harmony Search Algorthim，HSA）。考虑将该算法引用到配网无功优化研究中，旨在提高配电网络中用户电能质量和降低配电网络损耗。和声搜索算法可以解决配电网中无功优化问题，以IEEE-33节点与美国PG&E69节点配网为测试系统，并将该算法应用其中进行测试研究，实现算法的快速收敛，并取得了令人满意的结果。

1　和声搜索算法

和声搜索算法是一种新型智能启发式智能优化搜索算法［9］，是由韩国著名学者Geem等人提出，乐师在模拟创作音乐过程中设法反复调整各种乐器（决策变量）音调，旨在达到悦耳优美的音乐和声（全局最优），该过程由音乐师的审美标准来决定。音乐师通过和声保留、音调调节、随机选择3种方法来即兴创作。

1.1初始化问题及算法参数

一般情况下可以规定用如下形式的函数来表示优化问题：

式中：f（x）为目标函数；X为每个决策变量xi的值域；N为决策变量个数。对于离散型变量X=（xi（1），xi（2），…，xi（k））；而对于连续型变量X满足Lxi＜X＜ Uxi，Uxi与Lxi分别为每个决策变量的最大值和最小值，k为离散型变量可能个数。HSA参数分别为：和声记忆库大小（hHMS）；和声记忆库中存在的解向量个数；记忆保留概率（rHMCR）；和声记忆扰动概率（SPAR）；和声即兴操作次数（mNI）。和声记忆库（nHM）存储包含了所有解向量（决策变量值域）。

1.2和声记忆库初始化

和声记忆库中包含hHMS个和声向量，各个和声向量xi=（xi1，xi2，…，xiN）都是随机产生，并且每个和声向量皆由N个和声分量组成，其产生方式为

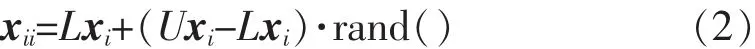
式中：i=1，2，…，hHMS；j=1，2，….，N；rand（）为0～1的随机数。为此便产生了和声记忆库nHM，形式为

尽管求解过程中可能产生违背约束条件的不可行解，然而该算法可以迫使搜索过程向可行解区域进行。静态罚函数［10］用来计算不可行解的惩罚代价，每个解向量总代价为

式中：αi与βj为罚因子。一般情况下，很难找出一条能决定罚因子大小的特定准则，因此，这些罚因子参数始终都与问题本身相关。

1.3即兴创作新和声

新的和声向量x′=（x′1，x′2，…，x′N）通过3种方式产生：和声保留、音调调节和随机选择。产生新的和声过程被称为即兴演奏。根据和声记忆保留条件，第i个变量=（-）。和声记忆库保留概率rHMCR（0＜rHMCR＜1）是指从和声记忆库nHM中选取定值的概率，（1-rHMCR）是指从和声记忆库可行域内选取定值的概率，具体为

式中：rand（）为0～1的随机数；Xi为每个决策变量的值域，且Lxi＜X＜Uxi。当rHMC等于0.85时，意味着hHMS以0.85的概率从当前记忆库HM中选择值，或者以0.15的概率从可行域中选择值。每个经过记忆选择得到的变量将被进一步检验是否需要音高调整。另外，在此次操作中，还会使用到SPAR参数如下：

式中：k为离散变量可能个数；m∈｛-1，1｝；rand（）为-1～1的随机数。

1.4更新和声记忆库

依据目标函数值大小，如果新的和声解向量x′=（x′1，x′2，…，x′N，）优于和声记忆库nHM中最差和声解向量，则该新和声解向量将会取代nHM中最差和声解向量，否则不予操作。可视为本算法的选择步骤，目标函数是衡量新和声向量是否存到和声记忆库中的标准。

1.5检查是否停止迭代

若算法迭代次数达到最大值，则计算终止；若未达到最大值，则继续回到产生新的解向量的步骤1.3 与1.4。

2　无功规划优化

无功优化旨在改善电压质量以及减少网络有功损耗，并且通过控制无功补偿或调节设备如发电机的端电压、变压器有载调压、可投切的电容器等。

2.1配网无功优化的数学模型

配电网无功规划优化主要是选择补偿点，并适当确定补偿容量，满足一定约束条件下，使得配网中网络损耗达到最小。无功优化数学模型由目标函数和各种约束条件［8］组成。

2.2目标函数

无功规划优化是个非线性、多目标函数优化问题，主要从经济性、稳定性及安全性考虑目标函数构成：

式中：Ploss为配电网络有功损耗，kW；β为单位电能损耗电价，元/kWh；τmax为最大负荷损耗小时数；ka和 kb分别为补偿设备的折旧维修费与投资回收费，万元；kc为单位容量补偿设备投资费用，元/kvar；Qci为节点i处电容补偿容量；km为补偿设备固定安装费用，万元。采用前推回代法计算潮流得出网损；λ为每个节点处电压越界函数ΔU的罚因子。

2.3变量及约束条件

无功优化数学模型中的变量包括控制变量与状态变量，其中控制变量由连续变量和离散变量组成，连续变量指发电机的端电压，离散变量主要是指电容器的补偿投切位置和变压器分接头可调位置等，而状态变量是指系统中发电机的节点电压和出力。本文研究的配网无功优化中状态变量和控制变量需要满足以下约束条件。

1）等式约束条件（潮流方程）

式中：Ui和Pi、Qi分别指节点j处的节点电压和节点i处的注入有功、无功功率；Gij、Bij分别是指配电网络节点导纳矩阵Gij±j Bij的实部和虚部；θ为节点i处与节点j处电压之间的相角差。

2）不等式约束

控制变量约束：

式中：Qjmax与Qjmin分别为节点j处补偿电容容量上、下限；NC为补偿电容的位置变化；Nnock为网络中的总节点数；Tmax与Tmin分别为可调变压器变比上、下限。

3）状态变量约束

式中：Uimax与Uimin分别为节点i处电压的上、下限。

3　和声搜索算法在配网无功优化中的应用

将和声搜索算法应用到配电网无功优化进行寻优，包括寻找控制变量最优值使得目标函数值最小。和声搜索算法实现过程如图1所示。

1）初始化配电网优化问题及算法参数。

2）初始化和声记忆库，并根据算法原理随机产生初始解向量。

图1　和声搜索算法流程

3）引用和声保留、音调调节和随机选择3种方式来产生新型和声解向量。

4）将和声记忆库中解向量进行更新，若新产生解向量优于和声中nHM最差解向量，则用新解向量代替最差解向量。

5）校核该算法的寻优终止准则，若达到既定的最大代数，则寻优终止，否则返回步骤3）、4）循环进行。

4　算例分析

为了测试和声搜索算法的工作性能，利用Matlab编程工具，分别以IEEE-33与美国PG&E69节点系统为例来进行测试验证。

该算法已知的测试参数如下：和声记忆库hHMS= 20，记忆库的选择概率为rHMCR=0.9，和声记忆扰动概率为SPAR=0.01，潮流计算电压允许误差为0.000 1，算法迭代次数要小于1 000。选择配电网络中补偿电容位置、补偿电容容量大小及网络中变压器的可调变比作为控制变量，考虑到在实际应用中要满足经济性要求，选取3个补偿电容位置进行无功优化，补偿电容位置在配电系统节点数之间变化，补偿电容容量为-300～0 kvar。

算例1采用文献［11］介绍的IEEE-33节点配电系统，该系统1000代优化时段图如图2所示，其表征网损优化结果与迭代次数之间关系。可知，HSA能跳出局部最优，并且其全局收敛性好，收敛速度快，网损优化效果好。表1所示为优化前后算法中设置的控制变量取值对比结果。图3为配电网络各个节点优化前后的节点电压分布，从图中易看出节点电压在优化之后得到显著提高，有效保证配电网络安全稳定经济运行。

另外，应用文献［12］中的电压稳定性判断原理对优化前后的配电网络分别进行电压稳定性分析，得到网络中各个节点的电压稳定裕度如表2所示，H为配电网络所有支路上的第2类电压稳定性指标集合，可反映网络中节点电压的抗干扰能力，H越大则节点电压的抗干扰能力越弱；而D=（1-H）表征整个网络所有支路上的第二类电压稳定裕度。可知，将和声搜索算法应用在配电网中优化后，网络中节点电压的稳定性得到较大提高。

表1　优化前后控制变量取值对比

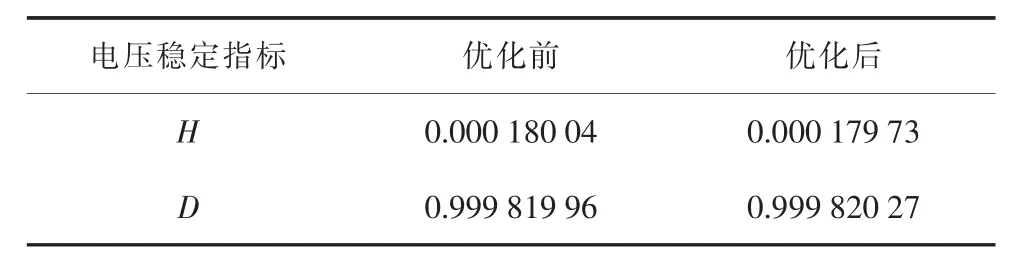
表2　优化前后节点电压稳定指标取值对比

再对该节点系统分别运用粒子群优化 （PSO）算法与和声搜索算法（HSA）仿真运行50次，每次运行迭代次数设为1 000，可以得出每种算法的最大网损优化百分比，最小网损优化百分比和平均网损优化百分比。表3所示为两种算法优化运行对比结果，图4所示为HSA优化50次对应的网损优化频率分布直方图。其中网损优化百分比指优化后网损与初始网损相比所降低的百分比。

表3　HSA与PSO算法优化对比

由表3可得出，两种算法结果可行，并且HSA优化效果优于PSO算法。

在网损优化结果上，HSA网损优化最大百分比和平均网损优化百分比要明显优于PSO算法，充分说明HSA的收敛能力。在算法稳定度上，该算法网损优化百分比大部分集中在16.5%到19%之间，而PSO算法网损优化百分比比较分散，大部分处在（15.5%，16%）与（18.5%，19%），说明HSA的收敛能力稳定度较高。

图2　IEEE-33系统优化效果

引用美国PG&E69节点系统作为算例2［13］，网络系统中共计有5个联络开关和73条支路，系统额定电压为12.66 kV，系统负荷为S=3 802.19 kW+ j2 694.60 kvar。对该系统运用HSA仿真运行，其网损优化效果如图4所示，说明该算法能被应用在实际大型配电系统无功优化中，并且收敛速度快，收敛稳定性好，在实际配电系统中具有一定可行性与有效性。

图3　优化前后节点电压变化情况

图4　美国PG&E69系统优化效果

由以上结果可得，和声搜索算法求解配电网无功优化问题是有效的、可行的，并且该算法的收敛稳定性还有很大提高空间。

5　结语

将和声搜索算法 （HSA）应用在配网无功优化中，结合我国配网存在的运行特征确定无功优化的数学模型，并且建立以网损最小作为无功优化的目标函数。利用Matlab编制出基于和声搜索算法的配网仿真程序，分别以IEEE-33与美国PG&E69节点系统为算例进行测试研究，仿真结果证明该算法收敛速度较快，验证了算法的可行性与有效性。

［1］张尧，王琴，宋文南，等.树状网的潮流算法［J］.中国电机工程学报，1998，18（3）：217-220.

［2］石韦，韦化，白晓清.含离散变量的大规模电力系统无功优化［J］.电力自动化设备，2007，27（3）：41-44.

［3］程莹，刘明波.含离散控制变量的大规模电力系统无功优化［J］.中国电机工程学报，2002，22（5）：54-60.

［4］曲绍杰，王绍然，刘明波，等．基于互补内点法的多目标静态电压稳定约束无功规划［J］.电力系统保护与控制，2010，38（23）：49-54.

［5］王瑞，林飞，游小杰，等．基于遗传算法的分布式发电系统无功优化控制策略研究［J］．电力系统保护与控制，2009，37（2）：24-27．

［6］A NGELINE PJ.Evolutionary optimization versus particle swarm optimization：Philosophy and performance difference［C］∥Proc of the 7th Annual Conf on Evolutionary Programming.Gemany：Springer，1998.

［7］刘玉田，马莉.基于Tabu搜索方法的电力系统无功优化［J］.电力系统自动化，2000，24（1）：61-64.

［8］闫若冰，唐巍.基于Pareto最优前沿的中压配电网多目标无功优化规划［J］.电力系统保护与控制，2010，38（24）：115-123.

［9］G EEM ZW，K IM JH，and L OGANATHAN GV.“A new heuris -tic optimization algorithm：Harmony search，”Simu lation，vol.76，no.2，pp.60-68，2001.

［10］R AYAPUDISrinivasaRao，S ADHUVenkataLakshmi Narasimham，M ANYALARamalinga Raju， et al.Srinivasa Rao.Optimal Network Reconfiguration of Large-Scale Distribution System Using Harmony Search Algorithm.IEEE Transactions on Power systems，2011，26（3）：1 080-1 088.

［11］GOSW AMISK，BASU SK.A new algorithm for reconfiguration of distribution feeders for loss minimization［J］.IEEE Trans on Power Delivery，1992，7（3）：1 484-1 491.

［12］刘健，毕鹏翔，杨文宇，等.配电网理论及应用［M］.北京：中国水利水电出版社，2007.

［13］BARAN ME，WU FF.Optimal capacitor placement on radial distribution systems［J］.IEEE Trans on Power Delivery，1989，4（1）：725-732.

Reactive Power Optim ization of Distribution Network Based on Harmony Search A lgorithm

ZHU Qinggang1，ZHANG Bo1，GUO Xiang2，ZHANG Jinliang1，LOU Tingting3
（1.State Grid Weifang Power Supply Company，Weifang 261021，China；2.State Grid Jinan Power Supply Company，Jinan 250012，China；3.State Grid Shandong Electric Power Research Institute，Jinan 250003，China）

A new artificial intelligence algorithm，harmony search algorithm（HSA），isapplied for reactive poweroptimization in distribution network.A mathematicalmodel，which takes minimum network loss as objective function，is built.Considering operating voltage requirements of distribution network，the solution of both compensation position and compensation capacity simultaneous is achieved through setting compensation legitimately.The harmony solution vector is updated bymeans of harmony consideration，pitch adjustment and random selection，which can keep the diversity of harmony，avoid the premature of convergence，and improve the convergence stability of HSA.Simulation results of IEEE-33-bus system and American PG&E69 system show thatthe calculationaccuracyand convergencestabilityof theproposed algorithm isbetter than resultsofPSOalgorithm. Resultsdemonstrate the feasibilityand effectivenessofHSA algorithm fordistribution network reactivepoweroptimization.

distribution network；reactive power optimization；harmony search algorithm（HSA）；harmony consideration；pitch adjustment

TM711

A

1007－9904（2016）03－0012－05

2015-11-18

朱庆钢（1988），男，工程师，从事输电线路运维检修工作。