小波变换在电压闪变信号中的检测分析
徐健,邵山
(西安工程大学 电信学院,陕西 西安 710048)
小波变换在电压闪变信号中的检测分析
徐健,邵山
(西安工程大学 电信学院,陕西 西安 710048)
为了实现对电力系统中电压闪变信号更为精确地检测,提出了小波变换的多分辨率分析的原理。由于小波变换具有较好的时频局部化特性,进而提取出电压闪变信号中的频率和幅值等参数。最后通过MATLAB仿真证明小波变换是一种更为有效的电压闪变分析方法。
电力系统;电压闪变;小波变换;多分辨率分析;MATLAB
电压闪变作为电能质量的重要指标之一,通常是由大功率冲击性负载的投入所引起的。电压闪变不仅会引起人的视觉疲劳也会影响到电子仪器、自动控制设备等正常工作[1]。如果能对电力系统中的电压闪变的信号进行有效的检测,将会给电压闪变的治理带来很大的帮助,对整个电力系统的安全稳定的运行也有十分重要的意义。
随着电力系统的不断发展,也逐渐形成了多种对电压闪变的检测方法。如傅里叶变换以及 Kalam滤波、最小误差二乘法、小波变换、S变换等。文中主要介绍前两种方法及其应用,最后通过对比,小波变换具有良好的时频局部化特性[2],可以更加方便运用到电压闪变信号检测中去。
1 电压闪变的数学模型
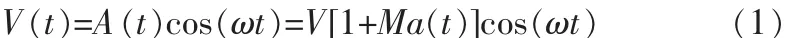
公式(1)中:V(t)是电网电压的额定值;A(t)为包络信号;ω代表信号的工频角频率;M是调幅系数,M通常为 0.01,最大可取到 0.1;a(t)为调制信号。调制信号表示为
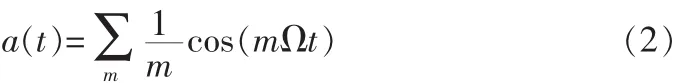
式(2)中,为调制信号的角频率,代表谐波的次数。
2 分析方法
2.1 傅里叶变换
傅里叶变换是信号分析的最重要的方法,他架起了时域和频域之间的桥梁。如果周期信号f(t)满足狄里赫利条件,则的傅里叶级数可表示为:
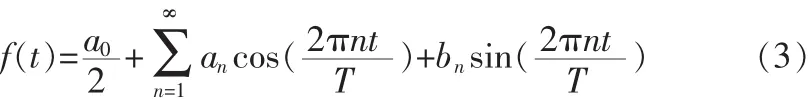
任何周期函数都可以表示为正弦函和余弦函数的叠加,并且这些正余弦函都是一组正交的函数基[3]。
式(3)中a0为常数分量,an、bn代表频率分量系数。其中:
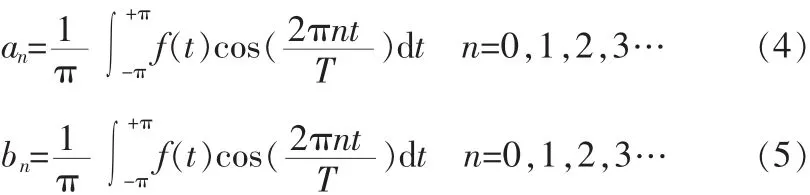
傅里叶变换可以将函数f(t)分解为不同频率的正余弦函数的组合,也说明了傅里叶变换能够准确地提取出信号的幅频特性。
2.2 小波变换及其多分辨特性
小波变换的含义是把基本小波的函数ψ(t)做位移τ后,在不同的尺度a下和待分析信号x(t)做内积[4]:
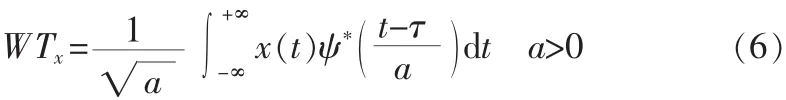
等效的频域表示为

式(7)中,X(ω),ψ(t)分别是x(t),ψ(t)的傅里叶变换。
将任意L2(R)空间中的函数f(t)在小波基下展开,称这种展开为函数f(t)的连续小波变换(Continue Wavelet Transform),其表达式为:
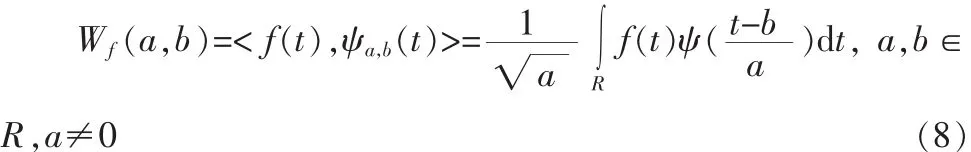
小波变换也是一种积分变换,Wf(a,b)是小波变换系数,函数 ψ(t)为基小波或母小波[5],a为尺度参数,b为平移参数,基小波波形表现为正负交替两端振荡衰减,均值为零。基小波 ψ(t)的傅里叶变换 ψ(w)满足容许性条件[6]:
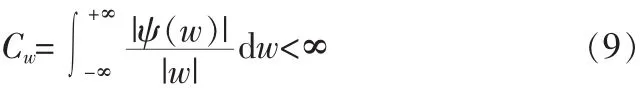
小波变换的多分辨率分析将信号在高频和低频频带上细化,得到越来越精细的时频描述,可以精确地再现信号在不同层次上的信息,多分辨率分析的方法就是将信号的信息在不同频带上体现出来的过程,多分辨率子空间V0可以用有限子空间来逼近[7],即:

Vj是尺度为j的尺度空间,也是反映空间Vj-1内信号近似部分的低频子空间;Wj是小波空间,也是反映空间Vj-1内信号细节部分的高频子空间[8]。Vj和Wj相互正交,从公式(7)又可以看出Wj是Vj在空间中Vj-1的补子空间。
对任意信号f(t)∈L2(R),将其进行多分辨率分解为:
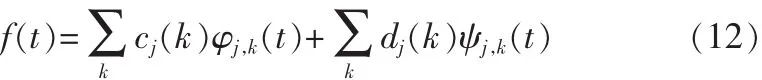
式(12)中:
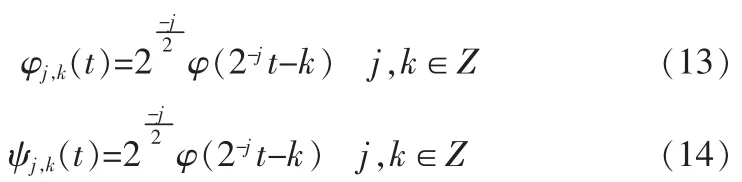
φj,k(t),ψj,k(t)分别代表尺度函数φ(t)和小波函数ψ(t)经过尺度和位移变化后的函数集合。cj(k)为尺度系数,dj(k)为小波系数。
3 仿真分析
含有突变信号的闪变模型为:
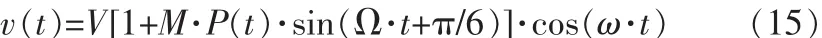

V=1V(标幺值),Ω=14 πrad/s,M=0.04,ω=100 πrad/s采样频率为800 Hz,采样点数为2 000,采样时间为2.5 s,电压闪变波形如图1所示
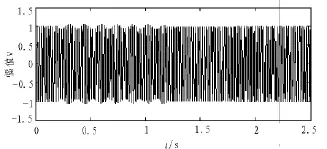
图1 含突变信号的闪变波形Fig.1 Flicker mutation signal waveform
经过快速傅里叶(FFT)变换得到的图形如图2所示。
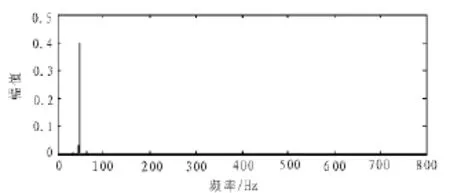
图2 含突变信号的FFT图形Fig.2 FFT transform graphic of mutation signals
由图2可以看出FFT只能读出闪变信号v(t)的幅频特征,并没有对闪变信号发生突变的时刻给以精确地区分,因而存在了某种程度的局限性。
根据多分辨率概念,采样频率为800 Hz,选用db20小波函数对闪变信号经过第一次分解后得到a1(0~200 Hz)和d1 (200~400 Hz)两个频带。再将a1分解得到a2(0~100 Hz)和d2(100~200 Hz)两个频带。以此类推经过六次分解后得到了a6(0~6.25 Hz)和d6(6.25~12.5 Hz)两个频带,此时7 Hz的闪变频率就落到了的频带上,低频的频带中已经没有了闪变信号分量,因此多分辨率分解到此为止。a1到a6为信号分解后的各层低频信号(逼近信号)如图3,d1到a6为信号分解后的各层高频信号(细节信号)如图4。另外在图4的d1和d2中可以观察到闪变信号波形有两个明显的突变点,分别对应着突变的开始时刻和结束时刻。这就是小波变换优越于傅里叶变换的突出所在。小波变换多分辨率分析能够将复杂的电压闪变信号频率划分到各子频带中,特别适合于调幅波中混合多种频率成分的情况。这是小波的多分辨率特性在电压闪变信号分析中的价值的最要的体现。
4 结束语
通过对闪变信号的仿真将傅里叶变换和小波变换的不同特点体现出来,仿真分析的结果可以看出小波变换在电压闪变信号的时频分析方面比傅里叶变换具有更强的分析能力。而快速傅里叶变换分析信号时只能反应频域上的信息,对时域不能做出任何的识别分析能力。小波的多分辨特性能将电压闪变不同频率的信号分离,从而能观察到信号的细微变化,也可以观察出突变的开始和结束时刻,因此小波变换换更适用于对电压闪变信号的分析。小波变换为我们的电压闪变检测工作提供很有价值的信息,对后续闪变问题的治理也具有十分重要的实际意义。
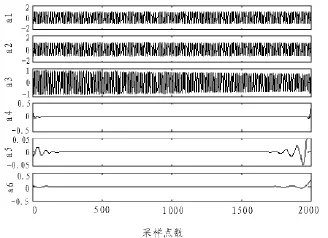
图3 信号v(t)小波分解后各层逼近信号Fig.3 Approximate components on each floor after the wavelet transform

图4 信号v(t)小波分解后各层细节信号Fig.4 Detailed components on each floor after the wavelet transform
[1]刘会金,吴玉蓉,熊玲玲.基于Daubechies小波的多分辨分解在电压闪变信号分析中的应用[J].继电器,2004,32(13): 6-10.
[2]张勇,管声启.基于小波提升分解的带钢表面缺陷检测[J].西安工程大学学报,2013(4):1-2.
[3]谢小磊.电压波动与闪变的小波分析[D].南京:河海大学,2006.
[4]郭晓丽,朱志松,许小梅.短时间闪变严重度Pst的计算方法的研究[J].南通工学院学报:自然科学版,2004,3(3): 66-69.
[5]郝晓平,党幼云.基于FPGA的信号奇异性检测[J].西安工程大学学报,2011(6):1-2.
[6]Dwight F M,Kraig J.OLEJNIZAK.小波基础及应用教程[M].杨志华,杨力华译.北京:机械工业出版社,2006.
[7]张志刚.电能质量讲座 第八讲电压波动与闪变[J].低压电器,2007(16):56-60.
[8]桑松,柴玉华,孙影.基于小波变换和快速傅里叶变换的谐波检测[J].电测与仪表,2012,49(559):29-32.
[9]任震,黄群古,黄雯莹.多层多分辨分析算法及在电力系统中的应用[J].电网技术,2012(6):5-7.
Detection and analysis of wavelet transform in voltage flicker signal
XU Jian,SHAO Shan
(College of Electronic Information of Xi’an Polytechnic University,Xi’an 710048,China)
In order to more accurately detect the power system voltage flicker signal,,this paper proposes the principles of multi-resolution wavelet analysis.Wavelet transform has good time-frequency localization properties and then extract the voltage flicker signal parameters such as frequency and amplitude.Finally through MATLAB simulation,it is proved that the wavelet transform is more effective in analysis of voltage flicker.
power system;Voltage Flicker;Wavelet transform;Multi-resolution analysis;MATLAB
TP
A
1674-6236(2016)04-0155-03
2015-04-14 稿件编号:201504139
陕西省教育厅专项科研计划(2013JK1015)
徐 健(1963—),男,陕西西安人,硕士,副教授。研究方向:电能质量检测、信号与系统等。

