由已知点探索未知点

季佳宁

在学习了平面直角坐标系这一章后，我们经常会遇到这几类问题：确定点的位置并将其与点的坐标进行转换；运动过程中，平面内点位置的变化；坐标系中的图形问题.今天我想和同学们共同分享我在平时的学习中是如何由已知点入手，通过数形结合求未知点的坐标.

在对平面直角坐标系的学习中我们知道，坐标平面内的点与有序数对（x，y）之间是一一对应关系，换言之，一个点对应且仅对应一对有序数.根据这一性质，我们一起来解决下面这一道例题.

例1 如图1所示，一个平行四边形的三个顶点为A（0，-1），B（2，-1），C（2，0），求另一个顶点D的坐标.

【解析】对于这道题而言，首先是对未知平行四边形进行分类，即分别以AB，AC，BC为对角线所构成，接下来就是本次探究重点，数形结合求点的坐标，我们以AB为对角线的平行四边形为例：由B、C点的纵坐标可以得到，线段BC的长=0-（-1）=1，那么线段AD的长也就为1，因为以AB为对角线，结合图像可以得到D1（0，-1-1）即D1（0，-2）.按照这样的思路，我们不难解得以AC为对角线时，D2（0，0）；以BC为对角线时，D3（4，0）.

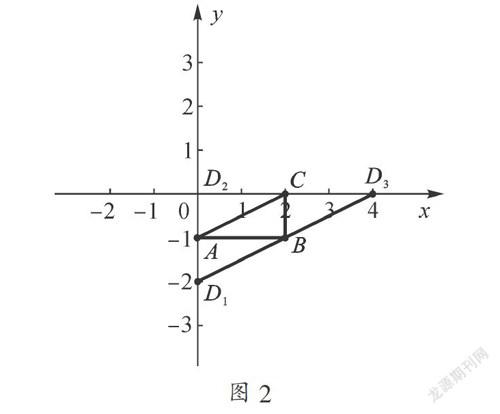
同学们可能觉得直接作图就可以得出答案，就本题而言，这个方法也是可行的，但是，如果某个点的坐标含根号，我们还可以直接作图看出吗？也就是说，多数题仅通过“形”来解是不可行或不合适的，还常需要“数”的结合，比如下面这一题.

例2 线段AB在平面直角坐标系中，经平移后A点由（2，1）至（5，3），那么原来坐标为（1，5）的点B平移后的坐标为_______.

【解析】已知点A的平移前后位置关系是本题的关键，分析其横坐标的运动可以得到，A点向右平移了3个单位长度，而分析其纵坐标可以得到，A点向上平移了2个单位长度，由此我们可以解得B点的运动规律，所以B（1+3，5+2），即B（4，7）.

通过上面两道题的练习，我们可以得出解决平面直角坐标系内由已知点求未知点的一般规律：首先由一个或多个已知点得到与未知点相关的长度关系，再利用数形结合的思想，将长度与图形或与坐标系联系起来（有时需添加辅助线），根据题意解得未知点的坐标.

最后一题是对于这次探究的拓展，所以相对上面有一些难度哦，但是利用已知点——长度——未知点的思路，问题自然就迎刃而解了.亲爱的同学，你有兴趣试试吗？

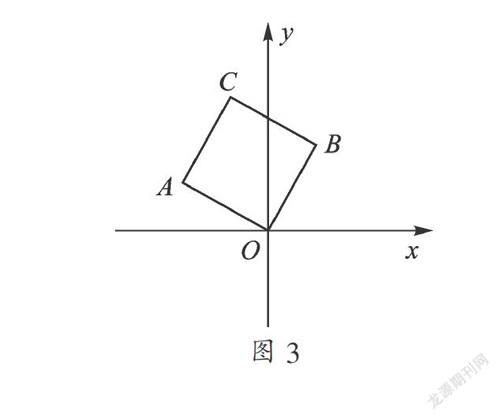
【探究再思考】如图3，正方形OACB的边长为4，且OB与y轴夹角为30°，求B，A，C点的坐标.

（指导教师：何林峰）