GIS分形法在西南三江地区断裂分析中的应用

黄　飞，何政伟，赵银兵，曹发生，王超维

（1.国土资源部地学空间信息技术重点实验室，成都 610059；2.成都理工大学地球科学学院，成都610059）

GIS分形法在西南三江地区断裂分析中的应用

黄飞1.2，何政伟1，2，赵银兵1，2，曹发生2，王超维2

（1.国土资源部地学空间信息技术重点实验室，成都 610059；2.成都理工大学地球科学学院，成都
610059）

本文以西南三江成矿带为例，采用分形理论的研究方法对其断裂构造进行定量研究，借助MAPGIS软件的网格和空间分析功能，计算出分维数D，通过解释其地质意义，利用ARCGIS对断裂构造进行频率分析显示：研究区分维数D在1.8对成矿较有利，控矿断裂（NNW-NW向）比一般断裂具有更高的分维值，而断裂构造分布最密集区并不是最有利成矿区。

GPS分形法；;断裂 ；MAPGIS；分维数；西南三江

西南三江地区是我国重要的成矿带，而断裂又是一种与成矿密切相关的构造[1]，因此找矿和断裂构造的研究紧密的联系在一起，但是传统的方法只能对断裂进行进行定性的研究描述，而分形理论对断层的定量研究提供了有效的方法。近年来将分形方法运用到断层研究的大都侧重于某个矿田或者区域性研究，金章东等（1998）[2]利用数盒子法计算浙江某矿田分维数，加大了工作量；皇甫岗等（1991）[3]将滇西北区断裂系解析为近南北向、北东向、北西向分别进行了分维数几何学研究；刘科等（2008）[4]对河北平原地区断层系进行了分形研究。本文根据成矿作用模式将三江地区断层系细分为4个成矿省，分别对四个成矿省进行分形理论研究。分形理论是当今十分活跃的新理论、新学科。分形的概念是美籍数学家芒德勃罗 （B.B.Mandelbrot）在20世纪70年代首先提出的，是研究不规则形体自相似性及复杂程度的一种理论。近些年广泛应用于各个学科领域。借助分形理论不仅有助于了解断裂带本身的性质，而且也可以对受断裂控制的矿产的分布预测起到一定的作用。

1 分形统计模型

设分形统计模型：

其中，r表示特征尺度；C＞0称为比例常数；D>0称为分维数;N（r）表示尺度大于等于r的数目（当分维数D前面的符号取负号，记为N（≥r））或尺度小于等于r的数目（当分维数D前面的符号取正号，记为N（≤r））。为了求出分维数D，将观测数据（N（r1），N（r2），…，N（rn））和（r1，r2，…，rn）绘在双对数坐标纸上，如果其散点大致分布在一条直线上的话，分维数D就可以利用直线的斜率求出，也就是说，将观测数据（N（r1），N（r2），…，N（rn））和（r1，r2，…，rn）代入（1）式，然后两边取对数，（1）式化为一元线性回归模型:

用最小二乘法求出斜率D的估算量，即为分维数D。[5]

近年来研究表明，断裂破碎过程具有随机自相似性，断裂的分布和几何形体具有分形结构，将分形理论应用于断层系统的研究具有实际地质意义[2]。从定量观点来观察断层的空间展布特征，断层系统实质上是由一系列的无规则的线状或面状几何体组成的集合[6]。应用分形方法可以求得反映断层系统空间分布复杂性的参数，即分维数。

2 西南三江地区断裂构造的分形分析

2.1西南三江地区断裂构造分析

西南三江地区地处特提斯－喜马拉雅构造域东部挤压、褶皱及推覆最强烈的地带，区域构造十分复杂，形成了规模大、数量多的弧形深断裂及大断裂和各种区域性断裂。三江成矿带经历了西部漫长的构造变动历史，构造复杂，张裂、碰撞和消减作用交替，形成数条板块结合带及深大断裂带，分割了不同的构造单元，构成了本区独特的构造、地貌景观。同时“三江”成矿区远高于全国的平均水平，是我国最重要的多金属富集区。三江地区的断裂主要由几条主干断裂（一级断裂）组成一个NNW向狭长状、中间部位急剧紧缩变窄、断裂变为SN向。并向北向南两方向扩张变宽的断裂构造[7]，与主断裂紧密相伴的还有几十条NNW-NW向展布的二级断裂，并在某个时期、某个地段也出现有NE-NNE向断裂带，这些断裂规模较小，形成时代较晚，多为切割、 穿插于北西向主断层。还有一些为数不少、规模大小各异的环状-似环状构造和推覆构造（如图1）。

一级主断裂（深断裂）主要有五条：

1）丁青-怒江主断裂（区内延展1 000km以上）。

2）北澜沧江-昌宁-双江主断裂（区内延展1 500km以上）。

3）金沙江-藤条江主断裂（区内延展1 600km以上）。

4）治多-甘孜-理塘主断裂（区内延展800km以上）。

对求解域进行划分，形成若干三角形单元e，然后设单元节点为1,2,3，则单元中某点温度可用节点温度进行表示，即：

5）金河-洱海-红河主断裂（区内延展1 000km以上）[7]。

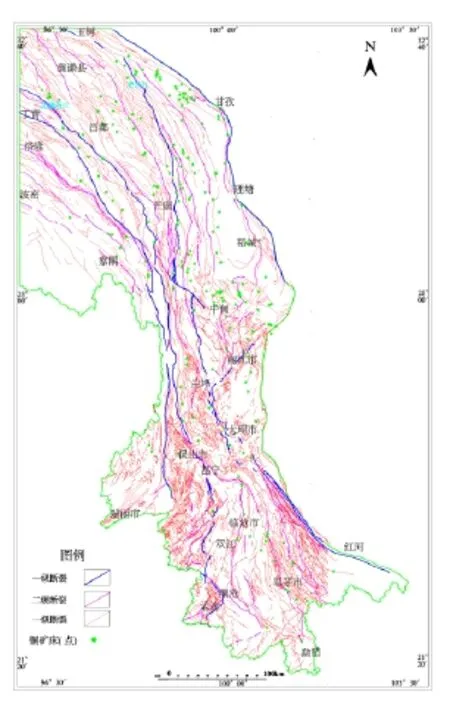
图1　西南三江地区1:100万断裂分级及铜矿分

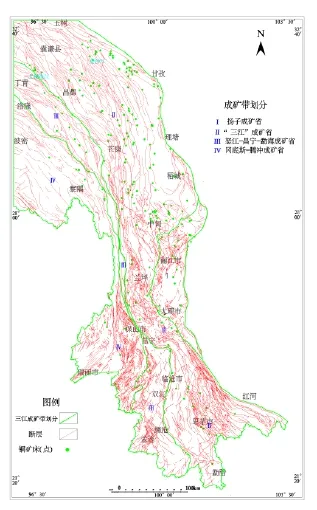
图2　西南三江地区1:100万成矿带划分及铜矿分布

五条主干断裂共同组成了三江地区的主断裂构造骨架，属于一级或超一级构造断裂带，二级断裂区内延展规模在200～850km左右，数量较多，三级断裂区内延展规模在160～600km左右，数量较多，形成时代一般较晚，部分断裂活动性强[7]。其中二级和三级断裂是主要的控矿断裂。

将1：100万西南三江地区断层图按地质背景和成矿作用模式分为四个成矿省：I扬子成矿省、II“三江”成矿省、III怒江-昌宁-勐海成矿省、IV冈底斯-腾冲成矿省，每个成矿省有包含多条成矿带。其中金属矿床主要集中在“三江”成矿省，约有78%的铜矿床（点）分布在“三江”成矿省。从图像上来看：三江地区北段区域主要是NNW向断裂，连续性相对好；中段区域断裂转为近SN向，少部分NW向断裂，连续性相对较好；东南段区域断层主要是NW向断裂，矿（床）点密集分布，西南段区域断层以NE向为主，铜矿床（点）较少。利用MAPGIS软件分别对四个成矿省断层进行了分形分析（因怒江-昌宁-勐海成矿省范围较小，矿床分布也较少，故和冈底斯-腾冲成矿省一起分析）。并分别对一级、二级、和三级断裂进行分形分析以作为对比（图2）。

2.2 利用MAPGIS软件提取数据

借助MAPGIS软件的空间分析功能，自动得到相关数据[8]，统计不同边长r下所得到的N（r），得到下列表格：

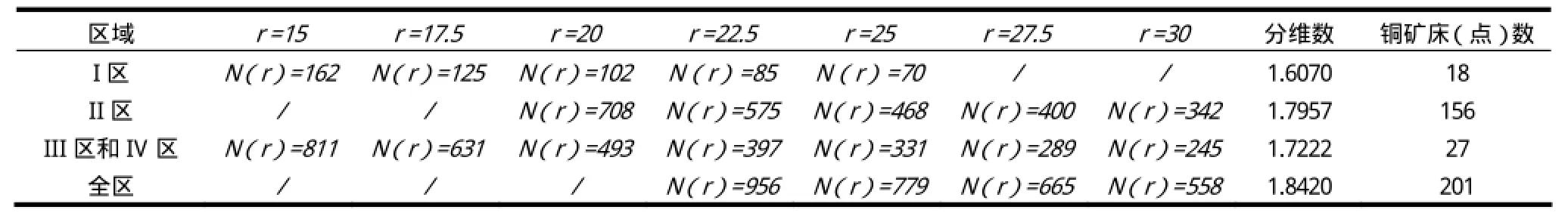
表1　西南三江地区断裂分维计算结果

表2　西南三江地区断裂分级后分维计算结果

利用EXCEL软件对上述数据在双对数坐标下作图，并添加线性趋势线，并显示公式和相关系数R的平方值得到下面一系列的方程式。同理得到一级断裂、二级断裂、三级断裂的分维数计算结果。

2.3断裂的分维数计算及其地质意义

应用以上分形方法，对三江地区进行了一系列网格分割，得到不同大小的网格单元，统计在不同大小网格中所包含断层的网格个数N（r）。在lgr-lgN（r）坐标中投点，用最小二乘法拟合直线，得到相应的直线方程为：

II区 ： lgN（r）=-1.7957lgr+5.1859 R²=0.9997

III区和IV区 ： lgN（r）=-1.7222lgr+4.9343 R²=0.9994

全 区： lgN（r）=-1.8420lgr+5.4700 R²=0.9995

一级断裂： lgN（r）=-1.0804lgr+3.8657 R²=0.9979

二级断裂： lgN（r）=-1.2937lgr+4.3811 R²=0.9995

三级断裂： lgN（r）=-1.7939lgr+5.3799 R²=0.9998

以上方程结果显示：I区域分维数D=1.607 0最小，结合断裂图像可知，I区域断层破碎、数量少，铜矿床（点）主要分布在断裂交汇处；II区域分维数D=1.795 7比其它两个区域都大，该区域主要是NNW-NW向断裂，断裂贯通性和连续性好，分支断裂相对较少，铜矿床（点）分布最多，说明NNW-NW向断裂构造的分维数D最大，而整个三江区域的控矿断裂主要就是NNW-NW向断裂，在NNW-NW向断裂带上分布的铜矿床（点）也最多。这就说明：分维数D越大，对成矿越有利；III区域和IV区域分维数D=1.722 2，该区域北段为NNW-NW向断层，断层稀疏，南段以NE向为主，断层密集，分支断裂较多，但是铜矿床（点）较少，说明NE向断裂分维值比NW向小，NE向断裂是后期形成的构造叠加有利于矿化富集；一级、二级、三级断裂所得到的分维数依次增大，这主要是因为分维数与断裂数目存在正相关关系，同时也和断裂的空间分布均匀程度有关。就断裂的发育演化而言，总的趋势是一个降维的过程，即由复杂几何结构的次级断裂向单一的连续型的大断裂过渡，这一观点已得到岩石破裂实验的证实[9]，所以断裂的分维数大小一定程度上反映了断裂的发育程度，即分维数越低代表断裂的发育程度越高。

为了能够更直观的解释所计算出的分维数与断裂之间的关系，笔者运用ARCGIS对断裂进行了构造频率分析。构造频率是指单位面积内线性构造的条数，在控制研究精度的基础上，本文采用10×10km标准网格将研究区进行划分，利用ARCGIS软件自动统计单位面积内线性构造的条数，生成断裂构造频率图[10]。构造频率图可以很直观的反映出断裂构造的分布情况（图3）。

图3中可以看出，频率高值区偏重在三江南段的云南西部兰坪-保山一带和东部部分地区。说明这些地区断裂构造分布密集，但是多为小型破碎断裂，而三江北段虽然断裂构造分布相对稀疏但多为大、中型断裂。结合之前分维数计算结果来看：频率高值区的云南西部兰坪-保山一带属于III和IV成矿省，频率高值区并不代表分维数也越高，铜矿床（点）主要集中在三江北段和中段的II成矿省（3～6条/100km²），故断裂构造分布最密集的地区（南段）也并不是最有利的成矿区。

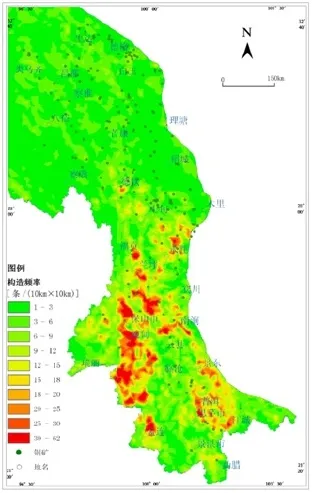
图3　西南三江断层构造频率与铜矿分布示意

3 结论

1）西南三江地区分维数越高，越有利于矿床形成。且控矿断裂（NNW-NW向）比一般断裂具有较高的分维值，这是因为NNW-NW向断裂结构复杂，构造活动强，这也与实际调查情况相符。研究区分维数均在1.8左右对成矿较有利，矿化密集地区（II“三江成矿省”）的分维值明显高于其他三个成矿省的分维值。因此分维数大小一定程度上可以做为判断矿化强弱的指标。

2）如果将三江区域的NW向、NE向、SN向断裂分开统计得到的结论应为：NW向断裂分维数＞NE向断裂分维数＞SN向断裂分维数。

3）从断裂分级后的计算结果可以看出：影响分维数大小的主要因素是断裂的数目和断裂的空间分布情况。断裂数目越少，相应的分维数也会越小。并且断裂分维数大小一定程度上反映了断裂的发育程度。

4）所提到的两种分形方法计算的结果不同，这主要是因为不同的分形方法计算得到的分维值不仅数目不同，而且地质意义也不一样，因此在讨论相应的结果时要结合其代表的地质意义。分形理论提供了一种定量分析自然界错综复杂事物的方法，但其针对的是自相似性的理想事物，自然界中实际断裂比理想的自相似性断裂复杂的多，因此分形理论还有一些不完善之处，需要在实践中不断完善。

[1] 陈国达. 成矿构造研究法[M].北京：地质出版社， 1978.

[2] 金章东，卢新卫，张传林. 江西德兴斑岩铜矿田断裂分形研究[J]. 地质论评，1998，44（1）：57～61.

[3] 皇甫岗，韩明，王晋南. 滇西北区断层分维数几何学的研究[J]. 地震地质，1991，13（1）：61～66.

[4] 刘科，李昌存. 河北平原地区断层系的分形特征分析[J].工程地质学报，2008，16（2）：206～210.

[5] 申维， 赵鹏大. 分形统计模型的理论研究及其在地质学中的应用[J]. 地质科学， 1998，33（4）：234～243.

[6] 刘晓东，李鹏举，徐景祯. 断层体系的分维数计算及其与深源气运移关系探讨[J]. 天然气工业，1998，18（2）：17～20.

[7] 王铠元. 依据卫星遥感影像研究结果综论西南三江地区构造特征[J].矿产与地质，1991，5（增刊）：1～32.

[8] 马佳国，李婷婷，李群，等. 基于GIS软件的分形方法在断层分析中的应用[J]. 长江大学学报（自然科学版），2011，8（1）：49～51.

[9] 谢和平，高峰，周宏伟，等. 岩石断裂和破碎的分形研究[J].防灾减灾工程学报，2003，23（4）：1～9.

[10] 赵银兵，何政伟，倪忠云，等. 云南省新平县地质灾害与线性构造的相关性研究[J]. 中国地质灾害与防治学报，2009，20（1）：70～73.

A Study of Faults in the Nujiang-Lancangjiang-Jinshajiang Area, Southwest China by MAPGIS Based on Fractal Theory and GIS

HUANG Fei1,2HE Zheng-wei1,2ZHAO Yin-bing1,2CAO Fa-sheng2WANG Chao-wei2
(1.Key Laboratory of Geo-Special Information Technology, MLR, Chengdu University of Technology, Chengdu 610059; 2- College of Earth Sciences, Chengdu University of Technology, Chengdu 610059)

The Nujiang-Lancangjiang-Jinshajiang area in Southwest China is a famous nonferrous and precious metal metallogenic belt. Faulted structure is of great importance to the metallogeny. This article studies quantitatively the faulted structures in the Nujiang-Lancangjiang-Jinshajiang area by MAPGIS based on fractal theory and GIS. MAPGIS is used for calculating fractal dimension D. ARCGIS is used for analyzing the frequency of the faulted structure. The fractal dimension of 1.8 is favorable to mineralization in this area. The fractal dimension of ore controlling faults is larger than that of common faults. Dense area of faults is not mostly favorable metallogenic one.

fractal theory; fault; fractal dimension; GIS; MAPGIS; Nujiang-Lancangjiang-Jinshajiang area, Southwest China

P228.4

A

1006-0995（2016）02-0339-04

10.3969/j.issn.1006-0995.2016.02.038

投稿日期：2015-5-24

中国地质调查局地质调查工作项目“西南三江成矿带中南段斑岩型铜矿遥感找矿模型研究与靶区优选（编号：12120113095400）”资助

黄飞(1991-)，男，湖北十堰人，硕士研究生，主要从事固体矿产勘查相关研究