行为保险学系列(五)伯努利效用函数的修正与保险决策
郭振华 上海对外经贸大学金融学院
行为保险学系列(五)伯努利效用函数的修正与保险决策
郭振华上海对外经贸大学金融学院
本文受国家自然科学基金面上项目(71173144)的资助。

郭振华,上海对外经贸大学金融学院保险系主任、副教授,兼任中国保险学会理事、上海保险学会理事。长期讲授《保险学》《保险公司经营管理》等课程,主持完成国家自然科学基金、教育部社科基金、上海社科基金项目各一项。
如“行为保险学系列(一)理性保险决策理论及其由来”所述,在新古典经济学和当今主流经济学教材中,一直采用的是伯努利1738年发明的效用函数。在人类世界,伯努利首次将财富的“金钱价值”和财富带来的“效用(心理价值)”区分开来,用边际递减的效用函数解决了圣彼得堡悖论,成为理性人进行风险决策的经济学准则。
伯努利效用函数有四大特点:第一,个体的效用是由其财富状态或财富结果决定的;第二,只要个体拥有一定的财富,无论规模大小,都会有一定的正效用水平;第三,随着财富增加,个体的效用会增加,但财富增加带来的边际正效用递减;第四,随着财富减少(或损失增加),个体的效用会降低,但人们的边际负效用递增。
表1是伯努利于1738年计算得出的一个效用函数版本,从中可以清晰地看到上述四个特点:第一,不同的财富值带来不同的效用值。100万达克财富水平的效用值是10个点,200万达克财富水平的效用值是30个点。第二,只要个体拥有一定的财富,无论规模大小,都会有一定的正效用水平。可以看到,无论财富多少,效用值都是正的。第三,随着财富增加,效用增加,但边际正效用递减。例如,财富水平从100万达克增加到200万达克时,效用增加了20个点(= 30-10);财富水平从200万达克增加到300万达克时,效用只增加了18个点(=48-30);财富水平从900万达克增加到1000万达克时,效用只增加了4个点(=100-96)。第四,随着财富减少,效用降低,但边际负效用递增。例如,财富水平从1000万达克降低到900万达克时,效用减少了4个点(= 100-96);财富水平从900万达克降低到800万达克时,效用降低了6个点(=96-90);财富水平从200万达克降低到100万达克时,效用大幅减少了20个点(=30-10)。
本文讨论效用函数对保险决策的影响,而保险主要承保纯粹风险,纯粹风险的特点是“要么遭受损失、要么没损失”,所以,本文主要研究个体在损失情境下的效用函数。在揭示伯努利效用函数缺陷的基础上,修正了损失情境下的效用函数,讨论了修正后的效用函数对保险决策的影响。
一、“财富值决定效用值”有误:未考虑参照点的影响

▶表1 伯努利1738年计算的效用函数
伯努利认为,一定的财富状态或财富值对应一定的效用水平,一定的效用水平代表着一定的快乐程度。如果A和B具有相同的伯努利效用函数,则,只要其财富水平相同,A和B的快乐程度就应该相等。但事实并非如此。
1.财富值相同,效用未必相等
案例1:假定张三和李四具有相同的伯努利效用函数,现在拥有相同的财富水平400万元,按照伯努利的效用理论,张三和李四的效用水平相同,快乐程度也应该相同。
但是,想想两人在400万元财富之前的状态吧!假定张三之前拥有200万元,李四之前拥有600万元,那么,张三和李四现在的快乐程度相同吗?答案是显然的,张三由于财富翻倍而非常高兴,李四则由于财富剧烈缩水而非常失望!所以,伯努利效用理论的预测是错误的。
再假定张三之前拥有1000万元,李四之前拥有500万元,现在两人拥有相同的财富400万元。则,按照伯努利的效用理论,两人现在的快乐程度应该是相同的,但实际情况是,张三明显比李四更加失望。伯努利效用理论的预测再次出现失误。
2.财富值为正,效用可能为负
按照伯努利效用函数,无论从过去到现在财富是增加还是减少,只要个体现在有一定的财富,他就有一定的正效用或一定的快乐程度。
但事实上,通过案例1可以发现,个体会将现在与过去进行对比,财富增加会使个体变得快乐(获得正效用),财富减少会使个体变得悲伤(获得负效用)。但伯努利效用函数未考虑人类会因财富减少而悲伤这一状况,因此,伯努利的效用理论是有缺陷的。
3.参照点不但重要,还会移动
从案例1可以看出,过去财富水平(或初始财富)基础上的财富变化决定着人们的效用和快乐程度,这个过去财富水平或初始财富是个体进行决策的参照点。卡尼曼和特沃斯基曾通过如下选择问题证明了参照点的巨大作用和伯努利理论的缺陷。
问题1:不管你原来有多少钱,现在再给你1000美元。请你在如下两个选项中选择一个:
A.50%的概率赢得1000美元,50%的概率什么也得不到;
B.肯定得到500美元。
问题2:不管你原来有多少钱,现在再给你2000美元。请你在如下两个选项中选择一个:
A.50%的概率损失1000美元,50%的概率损失为零;
B.肯定损失500美元。
可以看出,问题1和问题2带给被试者的财富的最终状态是相同的,本质上都相当于请被试者在如下问题中做出选择:
A.50%的概率赢得2000美元,50%的概率得到1000美元;
B.肯定得到1500美元。
按照伯努利效用理论,被试者对问题1和问题2应该做出相同的选择“B”。但事实上,对于问题1,多数被试者会选择B,但对于问题2,多数被试者会选择A,这就是参照点在起作用。对于问题1,被试者的参照点是“现有财富+1000美元”,并将选择编辑为盈利的风险问题;对于问题2,被试者的参照点是“现有财富+2000美元”,并且将选择编辑为损失的风险选择问题。由此导致了与伯努利效用理论预测截然不同的选择结果。显然,人类在决策中不仅会考虑参照点,还会经常移动自己的参照点,不考虑参照点的伯努利效用理论在对人类选择的预测上面临困境。
4.参照点对个体决策的重大影响
在上述案例中,伯努利效用函数仅考虑财富结果对效用的影响,没有考虑到个体会因财富变化而影响自己的效用水平或快乐程度(或悲伤程度),而财富变化必然有一个基准点,卡尼曼和特沃斯基将这个基准点称为“参照点”。正是基于参照点(往往是现状)的财富变化影响了人们的效用水平或快乐程度,人们的参照点才会随时发生变化,最终导致基于参照点的决策发生变化。
1979年,卡尼曼和特沃斯基在其发明的前景理论(ProspectTheory)中提出:第一,效用是随着财富的变化而出现的,而不是随着各种财富状态而出现的。或者说,财富状态本身并不带来效用,财富的变化才会带来效用;第二,既然考虑财富变化,就一定要考虑参照点,关注的是从参照点开始的变化;第三,变化自然会有两个方向,财富增长是赢,财富缩水是亏,财富增长带来正效用或快乐,财富缩水带来负效用或悲伤。这与人们在面对选择时的心理过程是极为类似的。
二、“财富减少导致边际负效用递增”有误
在伯努利效用函数中,随着财富减少(或损失增加),个体的边际负效用递增,如表1所示,财富水平从1000万达克降低到900万达克时,效用减少了4个点;财富水平从900万达克降低到800万达克时,效用降低了6个点;财富水平从200万达克降低到100万达克时,效用大幅减少了20个点。但是,由于以下两点原因,“财富减少,个体的边际负效用递增”这一说法站不住脚。
1.人们在面临损失风险时,往往呈现风险喜好
考虑下面的选择问题:
A.50%的概率损失1000美元,50%的概率损失为零;
B.肯定损失500美元。
按照伯努利效用函数,人们应该选B。因为在伯努利效用函数中,无论是盈利风险还是损失风险,个体的效用函数为凹函数,呈风险厌恶态度,财富期望值的效用总是大于财富效用的期望值,假定初始财富为W0,即
U(B)=U(W0-500)>U(A)=50%×U(W0-1000)+ 50%×U(W0)
但实际上,多数人都会选择A,这如何解释呢?可能的解释就是,人们在面临损失风险(纯粹风险)时,其效用函数是凸函数,呈风险喜好态度,随着损失增加,边际负效用递减,在将现有财富W0作为参照点的情况下,人们会认为:
U(B)=U(-500)<U(A)=50%×U(-1000)+50%×U(0)
2.无论财富增减,个体感受都遵从费希纳定律
心理学家很早就想知道当客观事物变化时,人们对客观事物的体验到底是如何变化的,例如,当水的温度、光的强度等物理量变化时,人们对水温和光的强度的主观体验值是如何变化的,这一领域称为心理物理学(Psychophysics)。
关于心理物理学,心理学家们最早提出的问题是,究竟物理刺激的强度变化多少才能让个体感觉到有差异,或者感觉到确实发生变化了。例如,室内灯光增加(或减少)多少瓦时,个体才能感觉到光线增强(或减弱)了。1834年,韦伯(Weber)提出,总的来说,某一种物理刺激,若要使人感觉到其强度的增加(或减少),必须使这一物理刺激强度在原有基础上增加(或减少)某个百分比,这一变化量被称为“最小可觉差”。于是,对于较小的物理刺激来说,只需要增加较小的变化量,个体就可感知到变化;但对于已经较大的物理刺激,就必须增加较大的刺激量,才能引起同等程度的注意。为了达到最小可觉差,需要增加(或减少)的刺激强度与原刺激强度的比率称为“韦伯分数”。举例来说,对重量差异感知的韦伯分数接近1/30,即只有将负重增加(或减少)原有负重的1/30时,人类才能感觉到负重确实增加(或减少)了。事实上,对于特定类型的感官刺激,其韦伯分数基本保持恒定,这一规律被称为“韦伯定律”。
1860年,心理学家费希纳(Fechner)提出,最小可觉差可以用一定数值的心理强度而不是物理强度来描述,并且认为,心理强度是物理强度的对数,这称为“费希纳定律”。这一定律后来被广泛接受,从此,心理强度指标逐渐走上历史舞台。例如,噪音的心理强度现在用“贝尔”或“分贝”(1贝尔=10分贝)来衡量,“贝尔”是一个心理强度指标而非物理强度指标,其计数单位就是以物理振幅的对数值来定义的,即“噪音的心理强度=log噪音的物理振幅”,噪音每增加1贝尔,表示物理振幅增大了10倍。费希纳定律所描述的对数函数的图形见图1。
对数函数显然遵循边际递减原则,也叫做边际报酬递减定律。经济学家们提出,这个定律不仅适用于描述心理强度与物理强度之间的关系,也适用于描述金钱与效用之间的关系。事实上,天才伯努利早在1738年就提出,金钱与效用之间的关系服从边际报酬递减定律(细节上与费希纳定律有所不同),比心理学界的费希纳定律早了120多年。1979年,卡尼曼和特沃斯基将心理物理学中的边际报酬递减定律运用到了前景理论中,认为,无论在参照点的右侧还是左侧,或者无论是收益变化还是损失变化,其引起的效用变化都服从边际递减定律。
3.小结:损失情景下边际负效用递减
基于以上两点原因,尤其是基于心理物理学的研究成果,伯努利效用函数中财富减少带来的边际负效用递增的结论是错误的,财富减少带来的边际负效用也是递减的。而边际负效用递减的函数,正好可以用来解释人们在面临损失风险时所呈现的风险追求行为。
三、损失情景的效用函数与保险决策
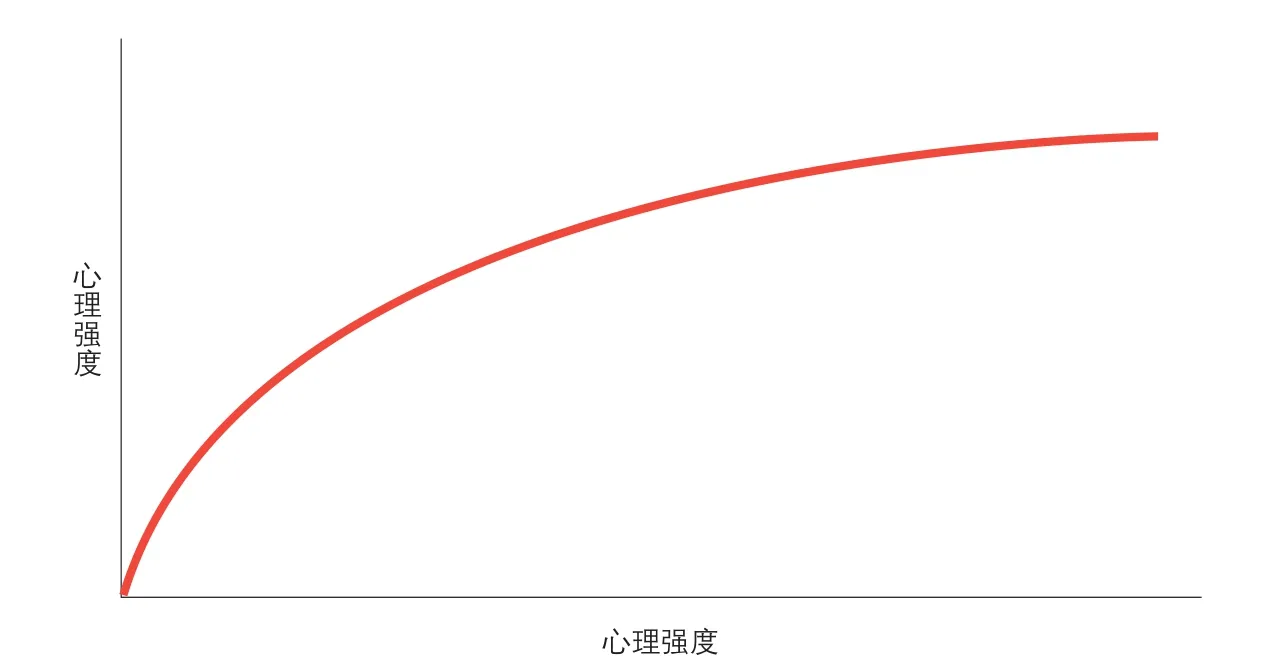
▶图1 费希纳定律:心理强度与物理强度的对数函数关系
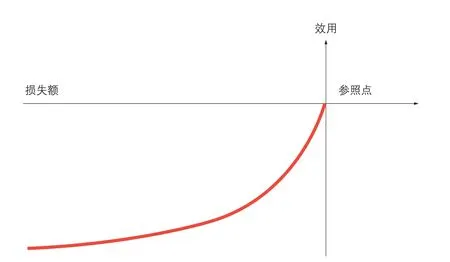
▶图2 损失情景的效用函数
1.损失情景的效用函数:边际负效用递减
如上所述,效用函数应该考虑参照点,财富减少带来的边际负效用递减。因此,损失情境下的效用函数如图2所示。损失情境下的效用函数呈现三个特点:第一,自变量“损失额”为基于参照点的负向变化,是负值;第二,因变量“效用”是负效用;第三,效用函数为凸函数,显示出边际负效用递减,即随着损失增加,个体对损失的敏感度降低。

2.保险决策:个体不愿投保
在损失带来负效用,损失部分的效用函数为凸函数的情况下,相较于伯努利效用函数(凹函数),在其他条件不变的情况下,人们的保险决策发生了重大变化,如图3所示。
在伯努利效用函数下,在保险公司仅收取纯保费或附加保费不高的情况下,人们愿意投保;但在如上凸效用函数下,即便保险公司仅收取纯保费,人们也不愿意投保。如图3所示,假定个体面临以的概率p损失L的风险,参照点为现状,保险公司仅收取纯保费pL。则,
U不投保=pU(-L)>U投保=U(-pL)
人们的选择将是不投保。如果保险公司还要收取附加保费,不投保的效用U不投保不变,但投保的效用U投保会沿着效用函数曲线继续向左下方移动,人们更加不会选择投保。个体的保险决策如表2所示。
四、结论
第一,伯努利效用函数存在两大缺陷:一是未考虑参照点的影响;二是在损失情境下边际负效用是递减而非递增。上述两大缺陷导致伯努利效用函数无法解释人们的喜怒哀乐,与现实严重脱节。
第二,在与保险决策相关的损失场景下,修正后的效用函数如图2所示,这也就是卡尼曼和特沃斯基发明的前景理论中价值函数的左半部分,呈边际负效用递减。
第三,在其他条件不变的情况下,边际负效用递减的效用函数将导致人们普遍不愿投保,无论保险公司是否收取附加保费。
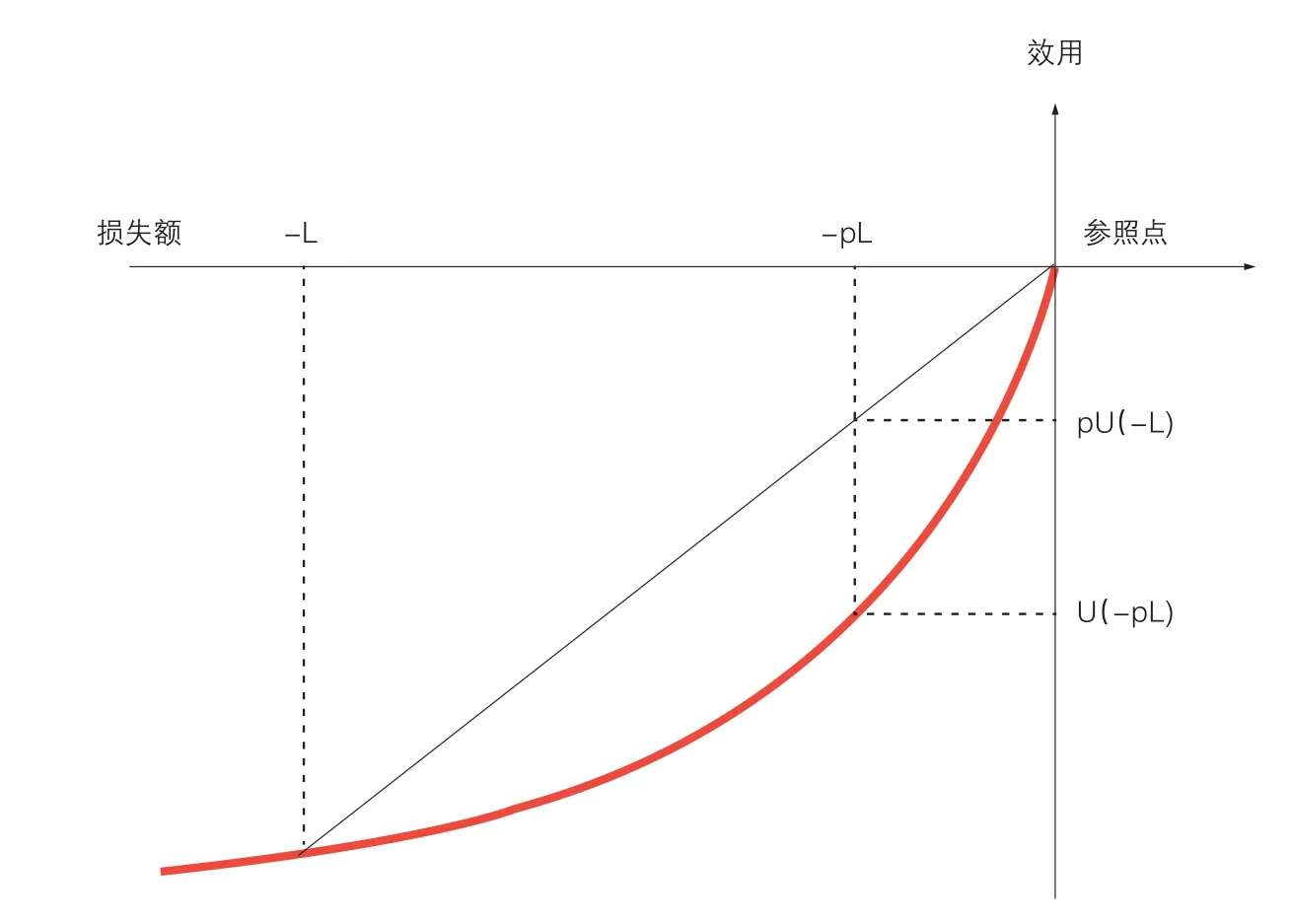
▶图3 凸效用函数下的保险决策

▶表2 不同效用函数条件下的投保决策

