基于RBF神经网络的天然气管道泄漏检测技术研究

高丙坤，郑仁谦，尹淑欣，张 莉，岳武峰

（东北石油大学 电气信息工程学院，黑龙江 大庆　163318）

基于RBF神经网络的天然气管道泄漏检测技术研究

高丙坤，郑仁谦，尹淑欣，张 莉，岳武峰

（东北石油大学 电气信息工程学院，黑龙江 大庆163318）

为了正确判断管道是否发生泄漏，本文采用混合学习方法对网络进行训练学习。通过将管道运行参数作为神经网络的输入，管道运行状态作为神经网络的输出，实现两者的非线性映射，以此来判断输入信号是否为泄漏信号，并选用K-means聚类方法和递推最小二乘法来确定网络参数。通过用天然气管道运行的实测数据对RBF神经网络进行了训练和测试，得到结果误差在可接受的范围内，从而证明RBF神经网络的方法可用于天然气管道泄漏检测的研究。

径向基函数（RBF）；聚类方法；非线性映射；泄漏检测

在天然气管道运输过程中，要对管道的泄漏情况进行实时监测，就要建立管道运行参数与管道运行状态二者关系的模型，但二者之间的关系无法用显式的线性函数来表达，而人工神经网络［1-3］理论打破了传统的思维模式，建立了良好的非线性模型。将神经网络应用于管道泄漏检测的研究开始于上个世纪末，根据其处理参数和应用背景的不同，主要介绍以下几种方法。北京大学的唐秀家，颜大椿等研究了管道泄漏后产生的力波在管道内传播的机理，首次将泄漏信号的特征值作为神经网络的输入数据，构建了神经网络模型对管道运行状况进行分类，进而判断管道是否发生泄漏［4-5］。后勤工程学院的研究人员针对多工况下管道泄漏检测数据量大，误报率高等问题提出了结合主成分分析和RBF神经网络的综合泄漏检测方法［6］。通过前人的深入研究和不断探索，神经网络在管道泄漏检测中的应用已经取得一定的成果。但在神经网络应用于管道泄漏检测的研究中，隐含节点的个数、中心、宽度的确定是决定RBF神经网络性能的重要因素，在前人的研究中并未对参数选取进行详尽研究，文中在此基础上运用混合学习方法来确定参数，结合实际现场数据证明此种方法行之有效。

1　RBF神经网络网络参数的确定

构建一个RBF网络要选择径向基函数的类型，确定隐含层数、隐含层节点的个数和基函数的中心c、宽度σ以及输出权值ω，而隐含节点的个数、中心、宽度的确定是决定RBF神经网络性能的重要因素［7-8］。如果这些因素的选取不恰当，就会造成无法实现从非线性的输入信息到线性输出信息的转换，导致RBF神经网络的性能降低。当RBF神经网络的基函数类型和隐含层节点个数确定后，网络的学习过程就是确定中心c、宽度σ和输出权值ω的过程［9］。

文中选择的是混合学习方法，包括两个学习阶段：自组织学习阶段和监督学习阶段。第一个阶段的主要目的是为隐层节点估计一个合适的位置，而第二阶段就是根据第一阶段估计的节点位置来计算网络的输出权值。

第一阶段采用K-means聚类方法确定神经元中心和高斯函数的宽度。

K-means聚类法即均值聚类法，是一种基于线性学习规则的无监督方法，可以保证快速收敛，这种算法简单且性能好。

1.1隐层神经元中心的确定

主要步骤如下：

1）初始化的中心 ci（0），1≤i≤N，从输入样本Xn（n=1，2 …N）中随机选择Nr个样本作为初始聚类中心（最终所得中心个数也为Nr）。原则上使ci（0）尽可能均匀地对天然气管道正常运行和管道泄漏时的样本数据抽样。

2）对输入样本按最邻近规则分组，在某一时刻t，计算每一个新输入的向量Xn（t）与每个聚类中心的欧式距离并获得最小距离：

3）将样本分配给距离最近的中心之后，重新计算聚类中心：

式中η（0＜η＜1）为学习步长。

4）将所有的样本分类后，对比新的聚类中心与之前的聚类中心以及分类情况是否有变化，若是，继续（2）至（3），若没有变化，停止计算。

1.2高斯函数宽度的确定

确定隐层神经元的中心后，采用公式（4）确定高斯函数的宽度

式中dm为所选中心之间最大距离，Nr为隐含层节点数。第二阶段采用最小二乘法确定网络输出权值。

基函数的参数ci和σi确定后，网络的期望输出可表示为：

其中φj（ci）是ci的一个固定函数，网络权值wi1（k）=［wi1（k），wi2（k）…wih（k）］T，ei为网络输出和实际输出的偏差。式（5）的零序列规划误差为：

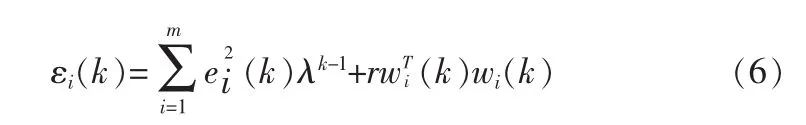
式中，λ∈［0，1］称为遗忘因子，r≥0为一个规划参数，则权值wij（k）可以推导得到。

通过上述最小二乘法迭代，求得网络的权值wij（k）［10］。

2　RBF神经网络天然气泄漏检测模型的建立

2.1输入输出节点的确定

在实际天然气管道运输过程中，当管道发生泄漏，管道内的气体密度、流量、压力、温度、负压波和次声波等都会受到影响［11-12］。在选择输入变量时，要尽量多的考虑因管道泄漏而变化的参数，根据项目现场传感器采集的数据情况，可以选择的输入变量有上、下游管道内压力，上、下游管道内流量，上、下游的次声波检测数据和上、下游的负压波检测数据。

一般来说，在一定范围内选择的训练样本越多，网络的输出误差越小，如果样本数据过多，神经网络的精度很难再提高［13］。文中选择了天然气管道正常运行状态下和管道泄漏状态下训练样本各10组，测试样本各5组。

因为所选参数表达的含义各不相同，参数之间数值相差较大，为了使各个参数对神经网络的影响力相同，我们对管道参数进行了归一化处理，统一参数的数量级［14］。

利用（8）式可将原始数据归一化到 ［-1，+1］区间作为输入量，可用（9）式将输出量还原为原始数据。

其中，y为归一化后在区间 ［-1，+1］的值，x为原始数据，xmax，xmin分别为原始数据中的最大值和最小值。表1分别给出了部分天然气管道在正常运行状态下和管道泄漏状态下归一化处理之后的参数数据。

2.2隐藏层层数的选取

隐藏层对于整个RBF神经网络的性能起着重要作用，隐藏层层数越大越可以提高计算的精度和降低网络的误差，但是也导致计算速度慢以及训练量增加［15］。经反复试验研究，拟采用含有单隐藏层的RBF神经网络。

2.3隐含层节点数的选取

隐含层的节点数即为所选高斯函数的个数，也就是由K-means算法确定的中心个数。根据初始化聚类中心时所选取的样本个数的不同，最后得到的中心个数也不同，那么隐含层的节点数也会有所不同，本文分别选取了8组，10组，12组样本数据初始化聚类中心，实验结果如图1、图2、图3所示。

根据图1、图2、图3可以看出隐含节点的个数过多或过少都会引起检测结果的误差增大，文中最终选择了10个隐含节点。由K-means算法得到的中心如表2所示。

2.4隐含层到输出层的权值

用最小二乘法得到网络输出权值如下表所示：

W=［-0.0964，-0.40044，-0.2442，0.0767，-0.1809，0.1203，

0.2242，-0.0140，0.0822，0.9315］

3　基于RBF神经网络的管道泄漏检测仿真实验

通过训练，可得到网络训练的误差曲线如图4所示。

根据图4的RBF神经网络样本训练误差曲线可知，训练后的RBF神经网络的实际输出结果与理想输出结果比较接近，经计算可得均方误差为9.57601×10-6，可以实现检测功能。

表1　天然气管道正常运行时参数归一化处理后部分数据表

图1　8个隐含层节点的RBF神经网络实际输出与理想输出结果

图3　12个隐含层节点的RBF神经网络实际输出与想输出结果

图2　10个隐含层节点的RBF神经网络实际输出与理想输出结果

图4　RBF神经网络样本训练误差曲线

4　结束语

文中采用混合学习方法对网络进行训练学习，其中选用K-means聚类方法和递推最小二乘法来确定网络参数。用天然气管道运行的实测数据对RBF神经网络进行了训练和测试，得到结果误差在可接受范围内，证明能够正确判断管道是否发生泄漏。

表2　RBF神经网络基函数中心

［1］龚骏，税爱社.多工况下基于 RBF神经网络的管道泄漏检测方法［J］.油气储运，2015（7）：759-763.

［2］宋源.国内外油气管道泄漏检测技术研究进展［J］.当代化工，2013（3）：42-45.

［3］李文军，王学英.油气管道泄漏检测与定位技术的现状与展望［J］.炼油技术与工程，2005，35（9）:49-52.

［4］唐秀家，颜大椿.基于神经网络的管道泄漏检测方法及仪器 ［J］.北京:北京大学学报 （自然科学版），1997，18（5）: 319-327.

［5］唐秀家.管道系统泄漏检测神经网络与模式识别方法［J］.北京:核科学与工程，1998，3（9）:220-227.

［6］闫少伟.基于神经网络的扣式电池自动化生产线故障诊断系统研究［D］.天津：河北工业大学，2006.

［7］Pan Jia Hua，The development of China's Long-Distance Pipeline Industry［J］.Pipe and Pipeline International，1984: 7-9.

［8］Khulief Y，Khalifa A.Acoustic Detection of Leaks in Water Pipelines Using Measurements inside Pipe［J］.Journal of Pipeline 2012（5）：47-54.

［9］鲁忠沂.基于RBF神经网络和小波变换的管道泄漏检测技术研究［D］.沈阳：东北大学，2010.

［10］Da Silva H V，Morooka C K，Guilherme I R，etal.Leak detection in petroleum pipelines using a fuzzy system［J］. Journal of Petroleum Science and Engineering，2005，49 （3）:223-238.

［11］朱爱华.卡尔曼滤波和序贯概率比检验在管道泄漏监测中的应用［D］.天津：天津大学，2006.

［12］肖姝颖，王帅.基于模式识别的天然气管道泄漏检测方法［J］.天津城市建设学院学报，2011，17（4）:268-271.

［13］刘道华，张礼涛.基于正交最小二乘法的径向基神经网络模型［J］.信阳师范学院学报：自然科学版，2013（3）:428-431.

［14］Henrique V，Morooka C，Guilherme I，et al.Leak detection in pipelines using a fuzzy system［J］.Petroleum Science and Engineering，2005（49）223-238.

［15］王立坤，赵晋云.基于神经网络的管道泄漏声波信号特征识别［C］//第四届全国信息获取与处理学术会议.2006: 2247-2249.

The natural gas pipeline leak detection technology based on RBF neural network research

GAO Bing-kun，ZHENG Ren-qian，YIN Shu-xin，ZHANG Li，YUE Wu-feng
（College of Electrical and Information Engineering，Northeast Petroleum University，Daqing 163318，China）

In order to correctly determine whether pipeline leakage occurs，this paper adopts a hybrid learning method for network training.We set the pipeline operation parameters as the input of neural network and running status of the pipe as the neural network output，realizing the two nonlinear mapping，in order to determine whether the input signal is leakage signal，and select K-means clustering method and the recursive least square method to determine the network parameters.With the measurements of the gas pipeline operation on training and testing the RBF neural network，we get the results in an acceptable error range，which prove that the method of RBF neural network can be used for natural gas pipeline leak detection.

radial basic function（RBF）；clustering method；nonlinear mapping；leak detection

TN206

A

1674－6236（2016）16-0078-04

2016-01-30稿件编号：201601290

教育部高等学校博士学科点专项科研基金 （博导类）课题 （20112322110003）；黑龙江省自然科学基金面上项目（E201332）；东北石油大学研究生创新科研项目（YJSCX2014-030NEPU）

高丙坤（1962—），男，黑龙江大庆人，博士，教授。研究方向：通信工程和控制工程技术开发。