外圆内正六边形同轴线中TEM波的场结构及其特性阻抗
王福谦(长治学院电子信息与物理系,山西长治046011)
外圆内正六边形同轴线中TEM波的场结构及其特性阻抗
王福谦
(长治学院电子信息与物理系,山西长治046011)
利用数值保角变换,给出外圆内正六边形同轴传输线内的TEM波的分布规律,绘制出其横截面上的场结构图,并计算出其特性阻抗。研究结论对于计算该传输线的衰减常数、了解其功率容量、考虑功率耦合及设计有关的有源器件均有一定的参考价值。
外圆内正六边形传输线;数值保角变换;TEM波;电磁场结构;特性阻抗
0 引 言
随着微波理论和技术的迅速发展,对新型传输线的研究提出了更高的要求。一系列新型的微波过渡部件、微波滤波器和新型定向耦合器的研究,是建立在对新型传输线的理论分析基础上的。因此,分析外圆内正六边形同轴线具有一定的理论价值和实用意义。对于复杂截面同轴线,由于其结构特点,要分析其场分布和各种特性参数,一般不能用常规解析法直接求解。本文拟利用数值保角变换法研究外圆内正六边形同轴传输线内TEM波的分布规律,绘制出其场结构图,并给出高精度的特性阻抗计算公式。
1 外圆内正六边形同轴传输线横截面的变换
将z平面上边长为a的正六边形的外部变换为w平面上单位圆的外部的变换函数[1]:
w=1.08651
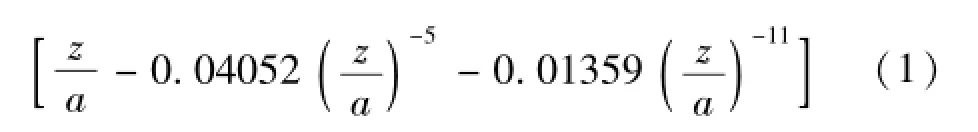
图1为外圆内正六边形同轴线的横截面,其内、外均为金属导体,边长和半径分别为a和b,则由式(1)可实现该传输线的横截面的变换,内正六边形变换为单位圆,外圆变换为位于之间的具有与正六边形相同对称性的闭合曲线[见图2中的闭合曲线,该曲线由式(1)通过MATLAB软件绘制],而r1、r2及其几何平均半径的数值如下[1]:
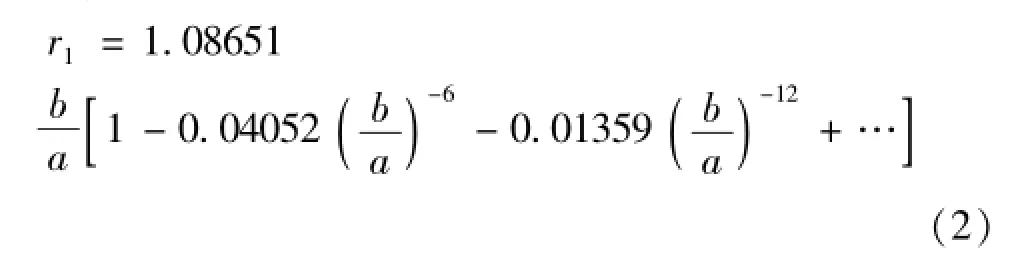
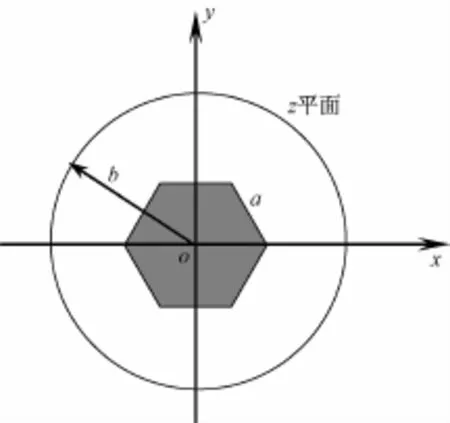
图1 变换前的外圆内正六边形同轴传输线的横截面
经上述数值保角变换后,z平面上的边长为a的正六边形和半径为b的圆,就映射为w平面上的单位圆和位于半径分别为r1、r2之间的具有与正六边形相同对称性的闭合曲线。由于在w平面上传输线内导体的横截面的形状为圆,外导体可近似看作半径为的圆(见图2),其内部电磁场在该截面上的分布近似呈轴对称性,故在w平面上可近似地按圆同轴传输线的情形来讨论电磁场分布规律。
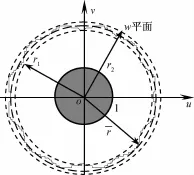
图2 变换后的外圆内正六边形圆同轴传输线的横截面
2 TEM波的电场和磁场的分布
外圆内正六边形同轴线中的TEM波的求解,可由静态场在相同边界条件下的解,得到其电场在此传输线横截面上的分布,乘以波动因子e-jβz得到电场的解,再由麦克斯韦方程获得其磁场的解[2]。据此,在圆同轴线内电场分布表达式的基础上,由数值保角变换可得外圆内正六边形同轴线中TEM波的电场强度和磁场强度的分布:
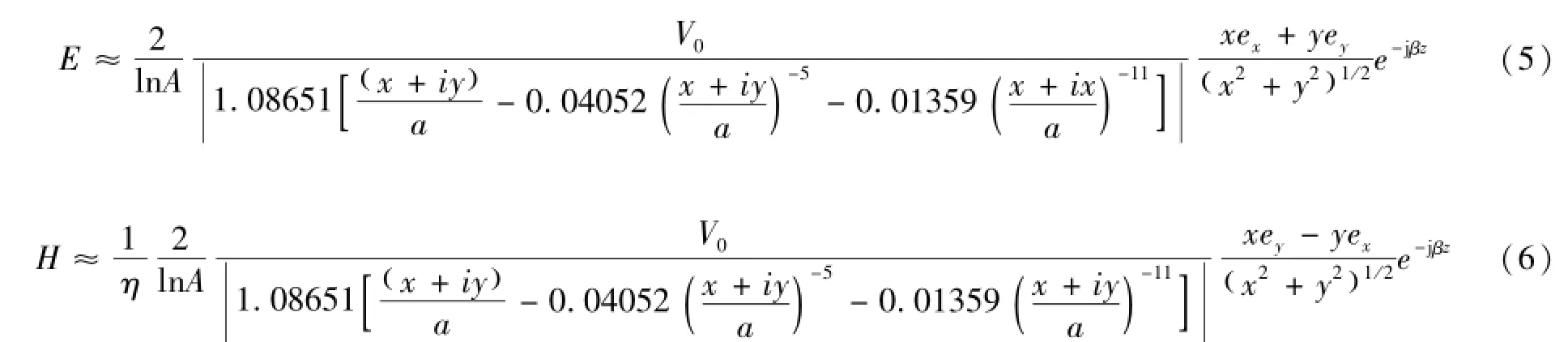
式中:V0为外圆内正六边形同轴传输线内、外导体之间电压的幅值;a和b分别为其内、外导体的边长和半径;β为沿传播方向ez上的相位常数,对于TEM波,波数为工作频率;ε、μ为传输线所填充介质的电磁参量,当传输线内部为空气时,介质的电磁参量取ε0和μ0);ex、ey为外圆内正六边形同轴传输线横截面上沿横、纵坐标轴方向的单位矢;式(5)、式(6)为外圆内正六边形同轴传输线中
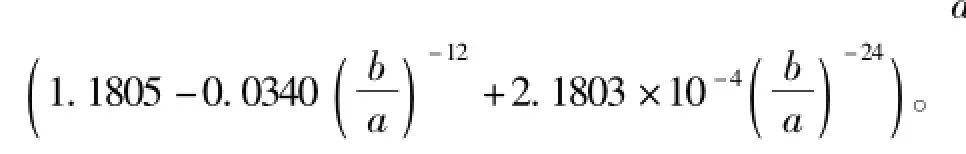
TEM波的电场与磁场分布的近似表达式。在得到该传输线电磁场的解析解(E,H)之后,由公式P=(式中的积分在传输线的横截面上进行)可计算出传输线上的传输功率,当其中的电场强度最大值取不发生电击穿的最大值时,所得到的传输功率值即为该传输线的功率容量;知道传输线中的电磁场的解析解之后,可以根据电磁场的分布情况,在此传输线上的恰当位置、选择恰当的耦合结构,实现该传输线与其他电磁结构之间的能量耦合;或在该传输线中的恰当位置接入有源器件,设计实现所需的功能。
图3为利用MATLAB软件所绘制出的外圆内正六边形传输线横截面上TEM波场结构图(其中a=2 mm、b=6 mm)。由于其内导体棱角上出现的电荷角分布效应,内导体表面附近的电场分布情况比较复杂。从图3可以看出,传输线内导体表面附近以外的电场在此传输线横截面上的分布呈现出中心对称,作出的图与预期结果(电场线与磁感线及导体表面均垂直)相符。图4为由HFSS软件仿真的外圆内正六边形传输线横截面上某一时刻TEM波的场结构图(其中a=2 mm、b=6 mm),将其场线分布与图3比较可以看出,MATLAB软件的数值模拟结果,与HFSS软件的结构仿真结果一致。这说明本文中研究外圆内正六边形传输线内TEM波场结构的方法正确,结论可靠。
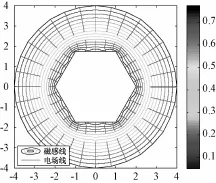
图3 外圆内正六边形传输线内TEM模的场结构

图4 外圆内正六边形传输线横截面上TEM波的场结构图
图5和图6为通过HFSS软件仿真出的外圆内正六边形同轴线内TEM波的三维电磁场结构图(其中a=2 mm、b=6 mm),场分布形象直观,便于对场结构的整体把握。在考虑功率耦合及设计有源器件时,也可参考传输线TEM波的场结构图,如上所述,在传输线上选取恰当位置,以实现该传输线与其他电磁结构之间的能量耦合或接入有源器件。由图3~图6及式(5)、式(6)可以看出,在传输线内部,愈靠近内导体表面,电磁场愈强.因此,内导体的表面电流密度较外导体内表面的表面电流密度大。

图5 外圆内正六边形传输线内TEM波的场结构图

图6 外圆内正六边形传输线内TEM波的场结构图
所以外圆内正六边形传输线的热损耗主要发生在截面尺寸较小的内导体柱上。
3 特性阻抗
经变换式(1)和式(4),外圆内正六边形同轴线的横截面已映射为半径分别为1和r-的两近似同心圆,由于映射前后传输线单位长度的电容量保持不变,这样就可由内、外半径分别为1和r-的同轴传输线的电容值,通过公式方便地求出此传输线的特性阻抗的近似值。据此,本文给出外圆内正六边形同轴线特性阻抗的计算公式如下:
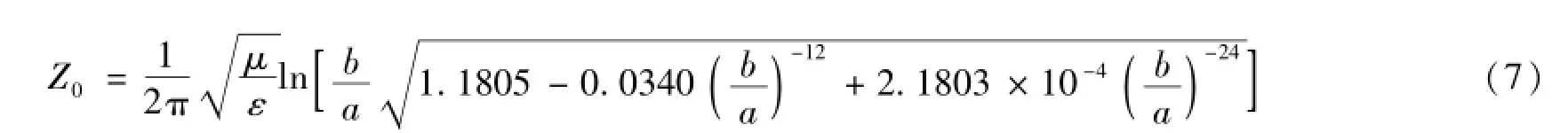
式中:ε、μ为传输线所填充介质的电磁参量,当传输线内部为空气时,介质的电磁参量取ε0和μ0;a 和b分别为外圆内正六边形同轴线内、外导体的边长和半径。
需要说明的是,由于电荷的角效应,内导体棱角处电荷密度大,而每边中点处的电荷密度小。对变换后的图2而言,内圆柱导体与无电荷角效应的外切圆弧之间的电容,要比其与内切圆弧之间的电容要大。所以,对于用内切圆和外切圆的边界尺寸取几何平均来“逼近”变换后的多边形外导体边界,由于交替出现了电容增大和电容减小的情况,故对计算总平均电容来说,电荷角效应的影响很小。因此,由式(7)计算出的外圆内正六边形同轴线特性阻抗值的近似值,具有较高的精确度。表1中分别列出了本文的计算方法与多极理论及矩量法所得的结果(介质为空气),其中R为外导体半径,r为内导体内接圆的半径。通过比较可以看出,本文的计算结果与多极理论的计算结果相当接近,相对误差的最大值为7‰,最小值为2.7‰,平均相对误差为3.9‰。表1中的计算结果也与文献[3-6]给出的数据几乎一致,相对差值均在2‰以内。由此也可佐证本文所给出的研究方法的正确性。文献[7]所给出的矩量法的计算结果稍有误差。
式(7)为外圆内正六边形同轴线特性阻抗的解析计算式。通过保角变换法计算复杂截面传输线的特性阻抗,公式推导过程简单,物理意义明确,精确度很高,可方便地计算任意尺寸的外圆内正六边形同轴线的特性阻抗。复杂截面传输线的特性阻抗也可用多极理论或矩量法计算,但多极理论准解析计算规则需要针对不同情形确定不同的内极、外极和极的次数等,原理相对复杂;而矩量法需对计算区域进行离散化处理,离散网格尺寸大小是求解精确性的关键,一般而言,网格越小越精确,但由于减小网格尺寸势必造成未知量数目的增加,使得存储量和计算量大幅增加,因此矩量法计算特性传输线特性阻抗的精度受计算机内存的限制,此即文献[7]所给出的用矩量法计算外圆内正六边形同轴线特性阻的数值,与其他方法相比较稍有偏差的原因。
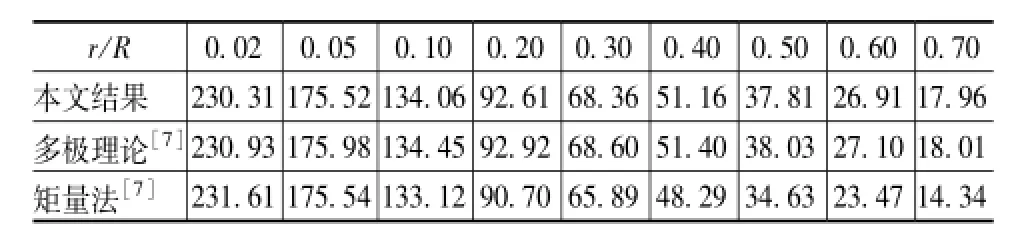
表1 外圆内正六边形同轴传输线的特性阻抗
4 结束语
计算机数值模拟的研究方法已成为继实验研究和理论分析之外的第三种研究手段。本文将理论分析与计算机数值模拟及场结构仿真相结合,对外圆内正六边形同轴传输线进行了研究,得到了该传输线内的TEM波的近似解析解,利用软件MATLAB 和HFSS绘制出了其场结构图,并给出了该传输线特性阻抗的计算公式。本文研究方法的物理意义明确、分析过程简单,所得结论对于了解传输线的功率容量、计算衰减常数、考虑功率耦合及设计有关的有源器件等都是不可缺少的,对传输线的设计与应用亦具有一定的理论意义。
[1] 任 伟,林为干.特种截面传输线的分析[J].电子科学学刊,1990,12(1):38-46.
[2] 沈熙宁.电磁场与电磁波[M].北京:科学出版社,2006:375-381.
[3] 佘显烨,方汉平.结合保角变换的优化模拟镜像法解多种截面形状同轴传输线的特性阻抗[J].电子科学学刊,1995,17 (3):283-289.
[4] Pan Sheng-gen.Characteristic imPedance of a coaxial system consisting of circular and noncircular conductors[J].IEEE. Trans.Microwave Theory Tech,1988,36(5):917-921.
[5] 徐善驾,盛新庆.任意横截面形状同轴线的高次有限元分析[J].电子科学学刊,1992,14(4):396-403.
[6] Wheeler H A.Transmission-line conductors of various cross section[J].IEEE.Trans.Microwave Theory Tech,1980,MTT-28:73-83.
[7] 吕文俊,曹 伟,朱洪波.具有屏蔽导体的多导体传输线的矩量法分析[J].南京邮电学院学报,2003,23(2):21-25.
The Field Structures of the TEM Wave in a Coaxial TransmissionLine With Circular-outer-Conductor and Regular Hexagon-inner-Conductor and Its Characteristic Impedance
WANG Fu-qian
(DePartment of Electronic Information and Physics,Changzhi University,Changzhi046011,China)
The distribution of the TEM wave in a coaxial transmission line with circular-outer-conductor and regularhexagon-inner-conductor is gotby using numerical conformalmaPPing,themaPof structureof electromagnetic field on its cross section is Plotted,furthermore,its characteristic imPedance is calculated.This research result to calculate the decay constantof the transm ission line,realize its Power caPability,consider its Power couPling and design the related active device has the certain reference value.
a coaxial transmission linewith circular-outer-conductor and regular-hexagon-inner-conductor;numerical conformalmaPPing;TEM wave;structure of electromagnetic field;characteristic imPedance
TM248.3
A
1672-6901(2016)02-0029-04
2015-05-05
山西省自然科学基金(2012011028-1)资助;山西省 2015大学生创新创业训练资助(2015432)
王福谦(1957—),男,教授.
作者地址:山西长治市城北东街73号[046011].

