地球同步轨道卫星多阶段任务可靠性建模
张 华,宗益燕,韦锡峰,陶 强,王 芳
(1. 上海卫星工程研究所,上海 200240;2. 上海师范大学 信息与机电工程学院,上海 200234)
地球同步轨道卫星多阶段任务可靠性建模
张 华1,宗益燕1,韦锡峰1,陶 强1,王 芳2
(1. 上海卫星工程研究所,上海 200240;2. 上海师范大学 信息与机电工程学院,上海 200234)
在分析地球同步轨道卫星首次变轨任务剖面的基础上,以模块化的思路进行卫星多阶段任务系统(phased-mission systems, PMS)建模,采用基于二元决策图(binary decision diagram, BDD)的静态多阶段任务可靠性分析方法和基于马尔可夫模型的动态多阶段任务分析方法来计算地球同步轨道卫星转移轨道段首次变轨的可靠性。经与传统非任务剖面可靠性分析方法的计算结果比对可知,基于任务剖面的可靠性建模分析方法可得到较为真实和精细的结果,有助于卫星的轻量化设计和研制效益提高。
地球同步轨道卫星;多阶段任务系统(PMS);二元决策图(BDD);马尔可夫模型;任务剖面;模块化建模;可靠性
0 引言
目前,卫星系统可靠性分析计算多采用可靠性框图模型[1](reliability block diagram, RBD)的方法,该静态模型简单、易于操作和理解,也因过于简化和保守,很多关键信息丢失,对卫星任务过程描述不够全面,无法反映航天产品复杂任务特性。
多阶段任务系统(phased-mission systems,PMS)的概念自1975年由Ziehms提出后[2],受到国外学者的广泛关注和研究,提出了不少的模型和解算方法。Dugan等将故障树分析、二元决策图(binary decision diagram, BDD)、马尔可夫模型相结合对PMS进行可靠性分析[3];Mura和Bodavalli等利用Petri网进行PMS可靠性建模[4];Xing和Dugan开展了广义PMS的可靠性研究[5]。国内在20世纪90年代末开始进行PMS的研究,钟季龙等利用递归算法和BDD模型解决了k/n(G)表决模型的计算效率问题[6];宋贵宝等研究了基于信息融合技术的复杂多阶段任务系统可靠性评估[7];胡小华等针对考虑共因失效的多阶段任务系统采用BDD方法进行建模和计算[8]。
本文针对地球同步轨道卫星的转移轨道段的任务过程,以姿轨控分系统、推进分系统和太阳电池阵分系统中的单机为对象,采用模块化的建模思想,运用BDD和马尔可夫模型开展卫星多阶段任务可靠性模型构建和计算,旨在提高可靠性分析结果的准确性和真实性。
1 PMS的可靠性研究方法
1.1PMS模块化建模思路
复杂不可维修的PMS存在元件之间的功能相关性和同一元件跨阶段的相关性。基于BDD的组合模型法仅适用于静态模型,整体使用状态空间的马尔可夫模型方法则会带来状态爆炸的问题,而模块化分析方法[9]结合了两者的优点。为了解决PMS相关性的问题,本文采用模块化分析方法。
PMS的模块化建模思路主要是:
1)首先将系统各阶段分别表示成故障子树,然后组合成系统故障树。利用 Rauzy方法[10]将每个故障子树分解成独立的子模块,对子模块进行合并整理得到系统的独立模块,使得各模块不存在元件间的功能相关性。
2)根据逻辑结构特点对系统模块进行分类,含有或门、与门和k/m门等静态逻辑门的为静态模块,含有顺序相关门、优先与门、冷备门等动态逻辑门的是动态模块。
3)采用BDD方法求解静态模块,马尔可夫模型方法求解动态模块,从而得到各模块的可靠性。
4)将每个模块作为系统故障树的底事件,再采用BDD方法求解得到整个系统的可靠性。
1.2基于BDD的静态多阶段任务分析
BDD是一种高效的布尔函数表达,同一个故障树在转换为BDD时,不同的底事件排序得到不一样的 BDD,相应的计算量也不同。目前,针对故障树底事件排序,学者们提出了多种方法,归结起来主要分为结构式和加权式[5],本文采用结构式中的从上至下、从左到右的排序方法。
BDD主要采用布尔表达式来进行逻辑运算。假设布尔表达式G和H分别为:

则G和H之间的布尔逻辑运算可表示为
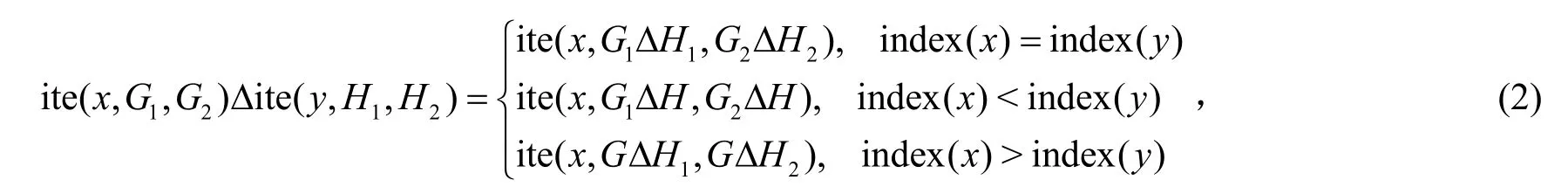
式中Δ为任意逻辑运算。
同一元件存在跨阶段相关性可用EZ方法[2]来处理,即用一组相互独立的微元件Ai(i=1,2,···,n)来表示某一元件A在不同阶段的状态,则元件A在阶段j的可靠度为
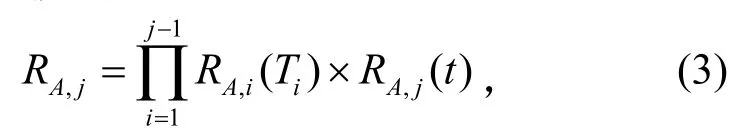
式中:RA,i(t)为元件A在阶段i的微元件Ai的可靠性函数,1≤i≤j;Ti为阶段i的持续时间,0≤t≤Tj。
BDD合成时,针对跨阶段元件,其微元件的布尔逻辑运算可采用向前阶段相关性运算和向后阶段相关性运算[11]。假设布尔表达式G和H分别为:
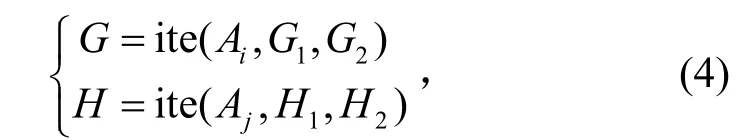
其中Ai和Aj为微元件在阶段i和j的变量,i<j。一般常用向后阶段相关性运算,即
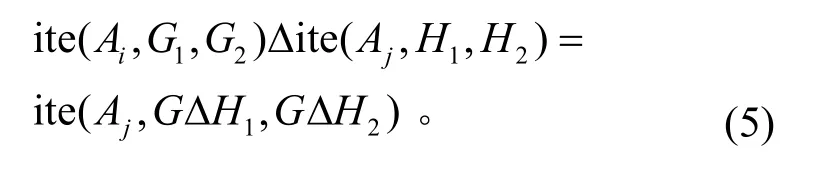
1.3基于马尔可夫模型的动态多阶段任务分析
采用马尔可夫模型链独立分析动态模块的每个阶段,前阶段的工作状态概率作为后阶段的初始状态概率,而失效状态在后一阶段的概率则置为0。该方法求解动态模块M可靠性的步骤为:
1)明确模块M的状态空间,令E={S1, S2,…,Sn}为 M 的状态空间,其中 W={S1, S2,…, Sk}和F={Sk+1,…, Sn}分别为模块M的正常状态集和失效状态集;
2)定义随机过程{XM(t), t>0},XM(t)=Si为模块M在t时刻处于状态Si(Si∈E),其概率用表示,即
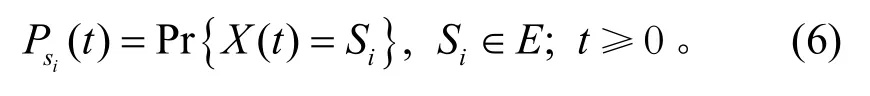
从而建立模块的状态转移图;
3)用状态转移图建立状态转移方程,根据阶段i初始时刻的模块M的状态概率,求解状态转移方程,得出阶段i结束时刻Ti模块M的各状态概率;
4)求解阶段 j(j=i+1)的马尔可夫模型链,模块M在阶段i结束时刻Ti为正常工作状态的概率作为阶段j的初始状态概率,在时刻Ti为失效状态的概率则被置为0作为阶段j的初始状态概率,得出阶段j结束时刻Tj模块M的各状态概率;将模块M在阶段j内所有正常工作状态的概率相加即为阶段i和阶段j的联合概率。
2 地球同步轨道卫星首次变轨任务的多阶段可靠性分析
2.1任务剖面分析
地球同步轨道(GEO)卫星发射后经历发射段、转移轨道段、准同步轨道段和同步轨道段等4个任务阶段。其中,星箭分离后至准同步轨道定点捕获之间的转移轨道阶段,卫星需进行多次变轨,星上产品的工作模式和工作状态较为复杂。本文针对转移轨道段的变轨过程进行细化,开展多阶段任务可靠性建模分析。
GEO卫星在转移轨道段涉及的姿轨控分系统和推进分系统的单机,以及单机的冗余备份情况详见表1。

表1 GEO卫星姿轨控和推进分系统产品配套表(部分)Table 1 Product matching table of attitude control system and propulsion system for GEO satellite
地球同步轨道卫星首次变轨需经过T1至T5共5个子阶段,分别是太阳捕获、地球捕获、地球指向、远地点点火准备和远地点点火,如图1所示。
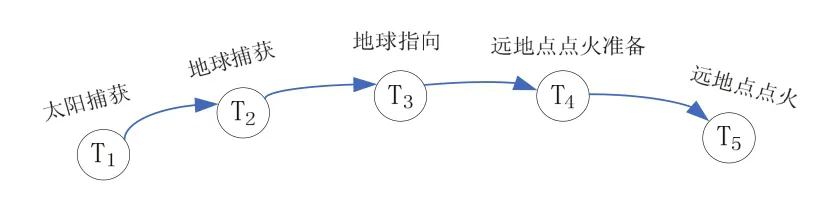
图1 地球同步卫星首次变轨任务剖面Fig. 1 Mission profile of geostationary satellite when it first changes the orbit
太阳捕获模式是星箭分离后姿轨控分系统默认进入的模式,以数字太阳敏感器 Cc、Cd,以及陀螺为测量部件,以10N推力器为执行部件,使卫星绕俯仰轴和滚动轴搜索太阳,发现太阳后卫星进入巡航模式。
地球捕获模式是地面注入姿态和姿态角速度偏置数据,以数字太阳敏感器 Cc、Cd,以及陀螺为测量部件,以10N推力器为执行部件,使卫星由巡航模式转为星体Oxz面内某A轴指向太阳,星体绕某 A轴慢旋搜索地球。当搜索到地球时,由地面指令转入地球指向模式。
地球指向模式是以数字太阳敏感器Ca或Cb,以及陀螺为测量部件,以10N推力器为执行部件,控制卫星-z轴指向地心。
远地点点火准备模式是以数字太阳敏感器 Cc和Cd,以及陀螺为测量部件,以10N推力器为执行部件,先使卫星绕z轴建立远地点点火姿态,然后使卫星绕+y轴旋转-90°,使+x轴指地,此时+z轴与前进方向的夹角就是所需的远地点点火姿态。
远地点点火是以490N发动机为执行部件,点火驱动卫星进行变轨。
2.2FTA建模
在对地球同步轨道卫星首次变轨任务剖面分析的基础上,运用故障树对5个子阶段进行建模,结果如图2所示。
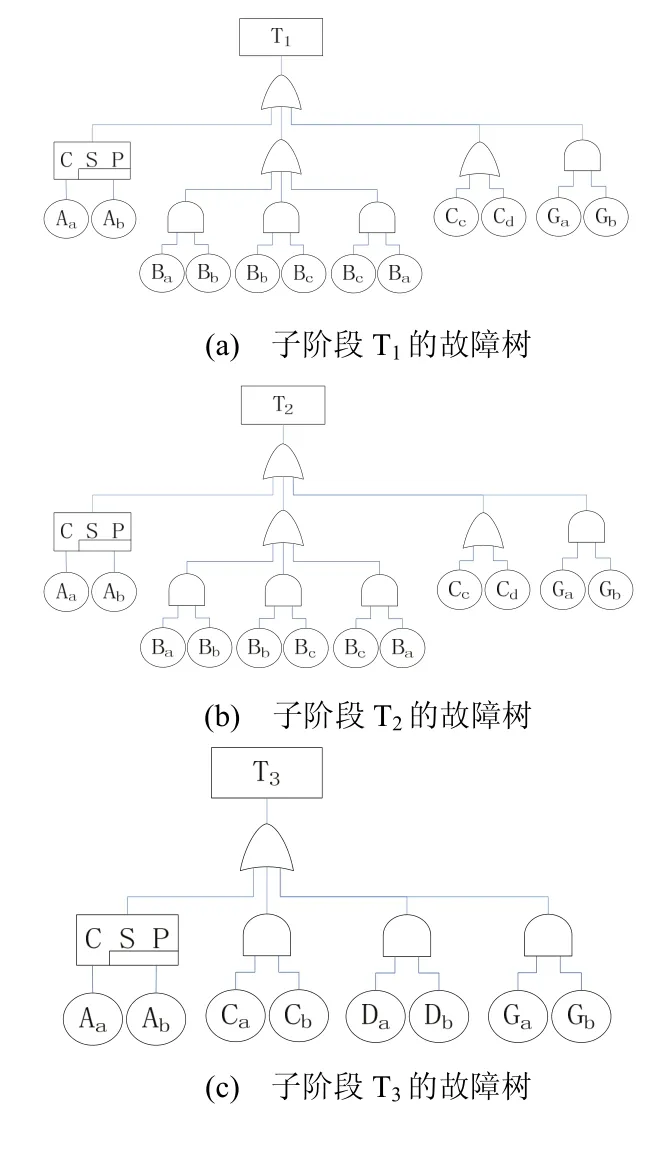
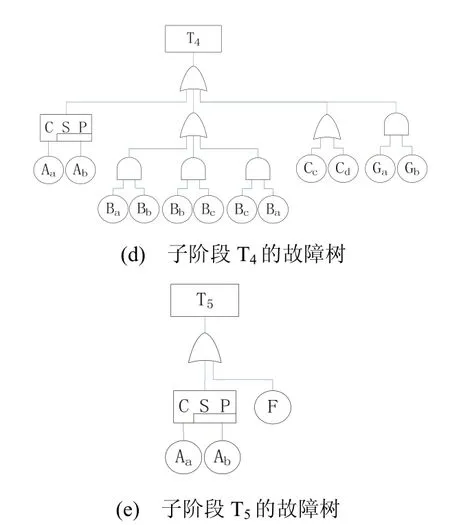
图2 地球同步轨道卫星首次变轨各子阶段的故障树Fig. 2 Sub-stage fault trees of geostationary satellite when it first changes the orbit
分析图2的故障树可知,运用模块化的思想对地球同步卫星首次变轨的故障树进行分类,可归类为8个独立子模块,分别是:M1={Aa, Ab},M2={Ba,Bb, Bc},M3={Cc},M4={Cd},M5={Ga, Gb},M6={Ca,Cb},M7={Da, Db},M8={F}。其中,M1属于动态模块,其余为静态模块。在此基础上,构建系统级的模块化故障树,如图3所示。

图3 模块化后的系统故障树Fig. 3 System fault tree after modular modeling
2.3BDD建模
采用从上至下、从左到右的故障树底事件排序方法,并结合同一元件的向后阶段相关性排序,得到变量排序为:M15<M14<M13<M12<M11<M24<M22<M21<M34<M32<M31<M44<M42<M41<M54<M53<M52<M51<M63<M73<M85。将子阶段T1到T5的故障树转化为BDD,如图4所示。


图4 地球同步卫星首次变轨各子阶段的BDDFig. 4 Sub-stage BDD of geostationary satellite when it first changes the orbit
采用逐步合并的思想,先将子阶段T1的BDD和子阶段T2的BDD合并,再将合并后的BDD与子阶段T3合并,依此类推,从而得到系统的BDD,如图5所示。
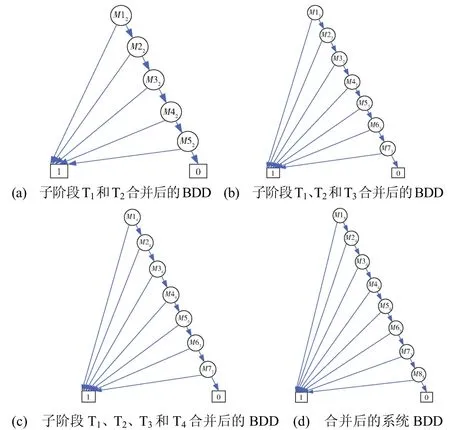
图5 地球同步轨道卫星首次变轨各子阶段BDD合并过程Fig. 5 Sub-stage BDD merge process of geostationary satellite when it first changes the orbit
2.4可靠性分析与计算
变轨段,姿轨控分系统和推进分系统各相关产品的失效概率分别为:λA=2.44×10-8min-1,λB=1.22× 10-8min-1,λC=6.10×10-8min-1,λD=2.44×10-8min-1,λF=1.72×10-7min-1,λG=1.22×10-7min-1。
以星箭分离时刻作为时间记录零点,首次变轨过程中各子阶段的持续时间分别为:t1=45min,t2=698min,t3=35min,t4=120min,t5=57min。
由于 M2~M8都是静态模块,则各模块的
可靠性计算为:

因此可直接得出各模块在各子阶段的可靠性,如表2所示,表中的可靠性为各模块在各子阶段末期的可靠性值。
M1为动态模块,其状态转移图如图6所示。其中,状态S1表示姿轨控计算机主份Aa和备份Ab都正常工作;状态S2表示姿轨控计算机主份Aa失效,备份Ab正常工作;状态S3姿轨控计算机主份Aa和备份Ab都失效。
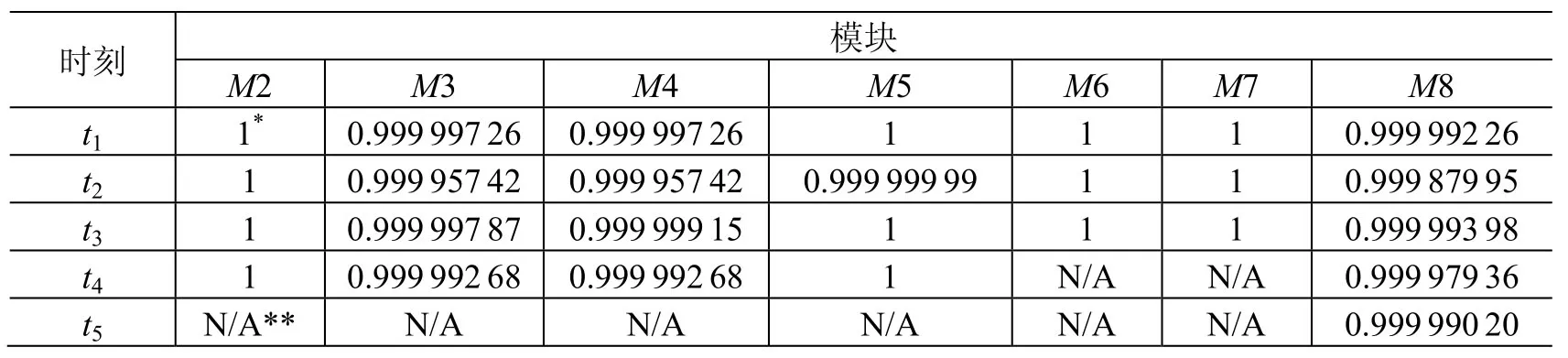
表2 静态模块在各子阶段的可靠性Table 2 Reliability of static modules in different sub-stages
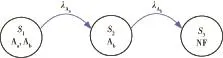
图6 模块M1的马尔可夫模型状态转移图Fig. 6 Markov state transition diagram of module M1
模块M1在各子阶段的工作状态如表3所示。
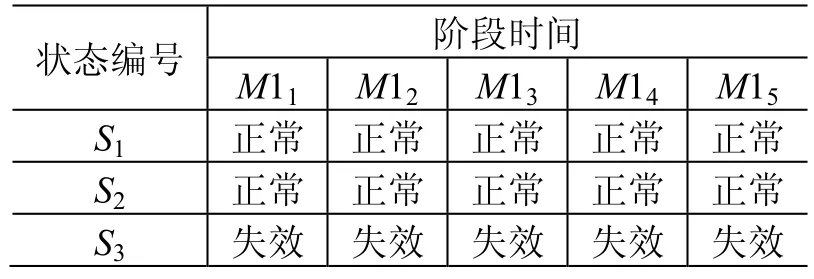
表3 模块M1在各子阶段的工作状态Table 3 The working status of module M1 in different sub-stages
根据图6建立模块M1的马尔可夫模型状态转移方程为:
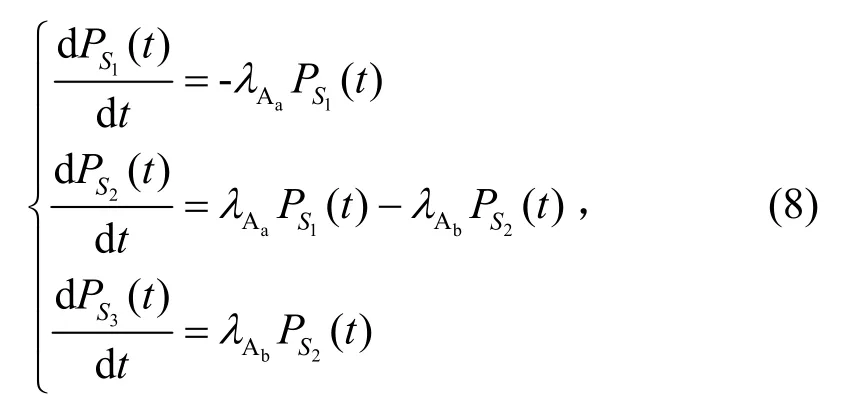

表4 模块M1在各子阶段初始时刻和结束时刻的状态概率Table 4 The state probabilities of module M1’s each sub-stage at the initial and the end moments
由表3可知模块M1在子阶段5的正常状态为S1和S2,因此首次变轨结束时刻模块M1正常工作概率为


表5 各模块正常工作的概率Table 5 The work probability of each modules
由图5可知,从M15到0的不相交路径集只有1条:则卫星首次变轨过程的可靠性为
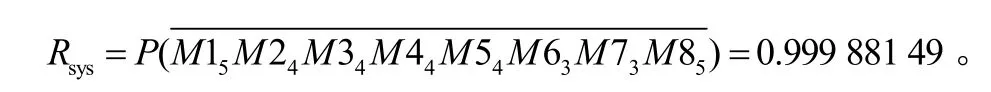
2.5基于任务剖面与非任务剖面的可靠性建模分析比对
作为对比,采用传统的非任务剖面可靠性框图方法对地球同步轨道卫星首次变轨进行建模。先分析卫星首次变轨参与的姿轨控分系统和推进分系统主要单机,再结合表1的产品主备份关系分析,建立的可靠性框图模型如图7所示。

图7 非任务剖面的地球同步卫星可靠性建模Fig. 7 Reliability model of geostationary satellite using non-mission profile method
根据2.4节列出的姿轨控分系统和推进分系统的产品失效概率,以及首次变轨的任务时间t=955min,可得到非任务剖面的卫星首次变轨可靠性为
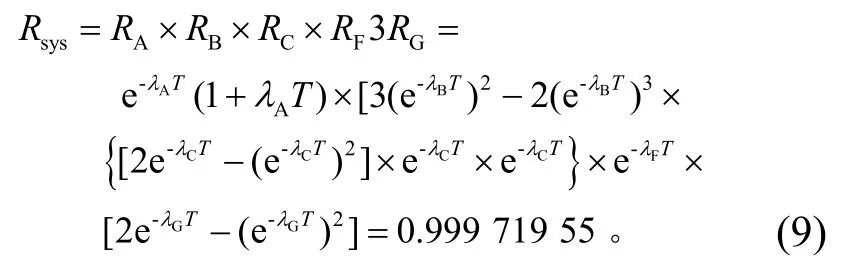
将上述结果与基于任务剖面的可靠性分析结果比对,可知:首次变轨结束时,卫星采用传统非任务剖面的可靠性建模分析的结果更为保守,但由于计算的任务时间短,且星上产品的失效概率低,因此两者实际值相差较小。
图8给出了首次变轨2种建模分析结果的比对,从图中可知:从任务开始至子阶段5结束时,基于任务剖面的卫星多阶段可靠性分析结果都高于传统的非任务剖面的,且随着时间推移,两者相差值逐渐变大,使得传统分析结果越来越趋于保守。即基于任务剖面的多阶段可靠性建模分析方法因对卫星任务过程的分阶段详细建模,可以得到较为精细、真实的计算结果。
当前我国卫星研制多采用高冗余的备份,尤其是姿轨控分系统单机常采用“豪华配置”以保证卫星的在轨可靠性,但是这样易造成卫星重量和研制经费的增加。因此,后续卫星研制时,在满足用户提出的卫星在轨可靠性要求的前提下,可适当优化卫星产品的冗余配置,为卫星轻量化设计和研制效益的提高提供数据支持。

图8 基于任务剖面与非任务剖面的可靠性分析结果比对Fig. 8 Comparison of geostationary satellite reliability obtained by mission profile method and non-mission profile method
3 结束语
本文采用基于任务剖面的可靠性建模方法求解地球同步轨道卫星首次转移轨道段的可靠性。经与传统非任务剖面可靠性分析方法计算结果的比对可知,基于任务剖面的可靠性建模方法可得到较为真实和精细的结果,有助于卫星的轻量化设计和研制效益提高。
后续将对基于任务剖面的可靠性建模方法开展进一步研究,解决含重复阶段系统的可靠性建模和分析优化,以期能够减少模型求解的计算量,提高本方法的工程可操作性。
(References)
[1] 可靠性模型的建立和可靠性预计:GJB 813—1990[S].北京:中国标准出版社, 1990
[2] ESARY J D, ZIEHMS H. Reliability analysis of phased mission[C]//Proc of the Conf on Reliability and Fault Tree Analysis, Society for Industrial and Applied Math (SIAM), 1975:213-236
[3] MANIAN R, DUGAN J B, COPPIT D, et al. Combining various solution techniques for dynamic fault tree analysis of computer systems[C]//Proc 3rdInternational High-Assurance Systems Engineering Symposium:HASE’98. Washington DC:IEEE, 1998:232-238
[4] MURA I, BONDAVALLI A, ZANG X, et al. Dependability modeling and evaluation of phased mission systems:a DSPN approach[C]//Proc Dependable Computing for Critical Applications. San Jose, CA, US:IEEE, 1999:319-337
[5] XING L, DUGAN J B. Analysis of generalized phased-mission system reliability, performance, and sensitivity[J]. IEEE Trans Reliability, 2002, 51(2):199-211
[6] 钟季龙, 郭基联, 王卓建, 等. 装备体系多阶段任务可靠性高校解析算法[J]. 系统工程与电子技术, 2016,38(1):32-35; 47 ZHONG J L, GUO J L, WANG Z J, et al. Research on phased mission based efficient reliability evaluation algorithm for equipment system of systems[J]. Systems Engineering and Electronics, 2016, 38(1):32-35; 47
[7] 宋贵宝, 张峰伟. 基于信息融合技术的多阶段可靠性评估方法研究[J]. 舰船电子工程, 2014, 34(2):41-43 SONG G B, ZHANG F W. Research on the method of multistage reliability assessment based on the information infusion technology[J]. Ship Electronic Engineering, 2014, 34(2):41-43
[8] 胡小华, 刘依路, 张如华, 等. 基于 BDD的多阶段任务系统可靠性[J]. 辽宁工程技术大学学报(自然科学版), 2013, 32(10):1415-1418 HU X H, LIU Y L, ZHANG R H, et al. Reliability based on BDD for phased mission systems[J]. Journal of Liaoning Technical University (Natural Science), 2013,32(10):1415-1418
[9] OU Y, DUGAN J B. Modular solution of dynamic multi-phase systems[J]. IEEE Trans Reliability, 2004,53(4):499-508
[10] RAUZY A. New algorithms for fault tree analysis[J]. Reliability Engineering and System Safety, 1993, 40(3):203-211
[11] 朱海鹏. 基于 BDD的多阶段任务系统可靠性建模分析[D]. 成都:电子科技大学, 2010:37-38
(编辑:冯露漪)
Phased-mission system reliability modeling of geostationary satellite based on mission profile
ZHANG Hua1, ZONG Yiyan1, WEI Xifeng1, TAO Qiang1, WANG Fang2
(1. Shanghai Institute of Satellite Engineering, Shanghai 200240, China;2. College of Information and Electrical Engineering, Shanghai Normal University, Shanghai 200234, China)
A modular approach is adopted to model the reliability of the geostationary satellite. The BDD and Markov methods are used separately to analyze the reliability of the static and dynamic modules of the satellite. Comparison of the calculation results with those obtained with the traditional reliability analysis method, shows that with the phased-mission system reliability modeling method, more accurate results can be obtained to provide a reference for the design of the light weight satellite.
geostationary satellite; phased-mission system (PMS); binary decision diagram (BDD); Markov model; mission profile; modular modeling; reliability
V474;TB114
A
1673-1379(2016)04-0439-07
10.3969/j.issn.1673-1379.2016.04.018
2016-01-12;
2016-07-19
张 华(1987—),男,硕士学位,从事空间环境、可靠性设计、多态系统可靠性等的研究工作。E-mail:zhanghua_seu@126.com。
——工程地质勘察中,一种做交叉剖面的新方法

