化学非平衡效应对返回舱气动特性的影响分析
吕俊明,程晓丽,俞继军,黄育群
(中国航天空气动力技术研究院,北京 100074)
化学非平衡效应对返回舱气动特性的影响分析
吕俊明,程晓丽,俞继军,黄育群
(中国航天空气动力技术研究院,北京 100074)
航天器返回舱再入过程中,高马赫数造成激波层内气体温度急剧升高,由此导致的化学非平衡效应对返回舱气动特性将产生显著影响。而飞行高度和速度的变化影响着化学非平衡过程,进而改变对飞行器气动特性的影响程度。文章通过求解三维Navier-Stokes流体动力学方程,利用耦合化学反应动力学模型对返回舱再入开展数值研究与机理分析,获得量热完全气体模型和化学非平衡气体模型的气动力预测值,分析飞行条件变化时化学非平衡效应对气动特性的影响规律。根据Apollo返回舱的AS-202飞行试验数据验证了计算模型与数值方法。对返回舱的模拟结果表明,高度不变、马赫数增大时,完全气体模型的气动特性预测值不变,化学非平衡效应影响下的轴向力系数、法向力系数和俯仰力矩系数与完全气体预测值的偏差均增大,化学非平衡效应增强;马赫数不变、高度增大时,化学非平衡效应造成的气动力预测值偏差也增大,配平攻角差值略有增加,化学非平衡效应同样增强。机理分析发现,飞行条件变化所造成的化学非平衡流场和压力分布变化是影响气动力变化的主要原因。
化学非平衡效应;再入;气动特性;高超声速;飞行条件
0 引言
航天器返回舱再入大气层时,头部形成的强激波对气流有强压缩作用,波后气体温度急剧升高,可达10000K以上,在返回舱周围形成高焓层,并伴随复杂的化学反应过程。化学反应发生后,大气组分和物理化学状态均会改变,造成返回舱表面压力变化,最终导致返回舱气动特性的变化[1]。使用简单的完全气体模型无法准确模拟流场的质量、动量以及能量分布[2],因而不能提供正确的气动数据。通常认为在高度50~80km、Ma>10的条件下,气体的流动处于化学非平衡状态,必须采用复杂的化学非平衡模型进行流场模拟。而随着飞行高度的下降,返回舱绕流经历冻结流动、化学非平衡和化学平衡等多个状态,因此化学反应对返回舱气动特性的影响是不断变化的。目前对于化学非平衡效应对气动特性的影响,以及影响随返回舱外形、弹道等多参数如何变化等问题,还没有统一的认识。
化学非平衡效应对返回舱气动特性的影响最早引起关注始于航天飞机高超声速异常现象,即大攻角飞行时,实际飞行中配平要求机身襟翼向下偏角达16°,为地面预测值(7.2°)的2倍之多。Shinn等[3]最早在20世纪80年代计算了航天飞机STS-2 在50~80km高度的气动特性,发现化学非平衡气体与化学平衡气体的计算流场差别较大。日本的HYFLEX高超声速再入飞行试验也于90年代证实了美国关于航天飞机气动特性的观点,即真实气体效应影响飞行器纵向配平的结果在Ma>10以后超出了地面预测值范围[4]。Holden等[5]在21世纪初的10年间通过试验研究了真实气体效应对几种高速再入飞行器性能的影响,结果表明真实气体效应减小了分离区的大小,提高了襟翼效率,降低了机翼后缘曲面上的压力,从而使飞行器的俯仰力矩减小、稳定性降低。Prabhu等[6]利用GASPex软件对航天轨道器开展了三维层流数值模拟,研究变化的比热比和化学反应模型对气动力的影响,结果发现在Ma=10和15时俯仰力矩受到的影响非常大。从已有的研究来看,无论地面试验,还是数值模拟,都发现化学非平衡效应对飞行器气动特性,尤其对配平特性有重要影响,但对不同状态下的影响规律及变化还没有定量的共性认识,对其中的机理也没有明确的结论。
国内近年来针对航天器返回舱高速再入开展了一些研究工作:梁杰等[7]分析了返回舱再入稀薄气体流域的配平特性和主要影响因素;詹慧玲等[8]采用完全气体模型对几类再入返回器的气动特性进行了对比分析;苗文博等[9]采用更为复杂的非平衡模型对气动热环境的影响进行了研究;吕俊明等[1]采用非平衡模型分析了非平衡效应对气动力特性的影响。以上研究对气动特性预测和化学非平衡效应影响有了一定的认识,但还没有针对化学非平衡效应对气动特性影响规律展开研究。
本文以返回舱再入为背景,通过数值模拟研究其在化学非平衡效应影响下气动特性的变化规律,并通过机理分析解释变化原因,对高超声速化学非平衡流动数值研究和返回舱气动、轨道设计有重要的学术意义和工程价值。
1 数值方法与验证
1.1控制方程与计算方法
为了数值模拟求解三维层流 Navier-Stokes方程,需将耦合化学反应动力学模型中的直角坐标系三维可压缩层流N-S方程写为

式中:U为守恒型独立变量;F、G、H分别为x、y、z方向的对流项通量;FV、GV、HV分别为x、y、z方向的输运项通量;S为化学反应源项;t为时间。具体表达式可参见文献[10]。
对流项∂F/∂x的计算采用 AUSM+-up格式和minmod限制器,其界面值通过MUSCL(monotonic upwind scheme for conservation laws)方法得到;黏性项∂Fv/∂x采用二阶中心格式;∂U/∂t采用LU-SGS (lower-upper symmetric Gauss-Seidel)隐式求解方法。
计算中涉及的完全气体均为量热完全气体,参数按空气给定,后文叙述时简称完全气体。非平衡模型中热力学和输运参数通过温度拟合多项式得到[11];混合气体的相关参数由Wilke公式计算;化学反应源项通过有限速率化学反应模型得到。根据本文飞行条件,选择Park的七组元(O2,N2,O,N,NO,NO+,e-)、六反应模型[12],具体参见表1。

表1 化学反应模型Table 1 Chemical reaction model
1.2程序验证
采用Apollo返回舱的AS-202飞行数据[13]和国外学者的热化学非平衡计算结果,对计算模型和数值方法进行验证。计算条件如下:Ma=27.2,攻角α=17.5°,以头部直径为特征长度的雷诺数 ReD= 194111,总焓H0=32.842MJ/kg。物面采用非催化无滑移等温边界条件,壁温Tw=1500K。返回舱外形如图1所示。
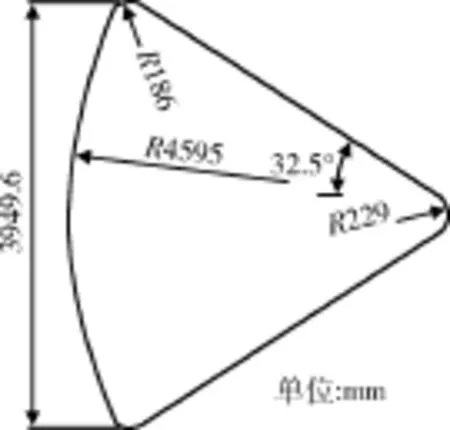
图1 Apollo返回舱外形尺寸Fig. 1 Shape and dimensions of Apollo re-entry module
图2是计算得到的对称面流线结构,包括驻点区、激波层、膨胀波区、剪切层、压缩波区和旋涡。在返回舱后体尾迹流动中,背风区有奇点形成。

图2 对称面流线Fig. 2 Streamlines in symmetric plane
表2列举了本文计算结果和AS-202飞行数据、文献数据[14]的对比。结果显示:计算得到的气动特性数据与飞行数据符合较好,升力系数相差8.42%,阻力系数相差7.21%,升阻比相差0.08%;较之文献数据,本文计算结果与飞行数据整体符合得更好。

表2 Apollo返回舱气动特性数据对比Table 2 Comparison of aerodynamic characteristics of Apollo re-entry module
2 计算结果与讨论
2.1计算模型与条件
选用“联盟号”返回舱为计算模型,其外形如图3所示,具体尺寸可参见文献[13]。以头部顶点为坐标原点,质心位置为(0.48m,0.04m,0)。壁面设为非催化无滑移等温边界,Tw=1000K。选定高度H=60km,Ma=20、24和28,研究化学非平衡效应对气动特性的影响随马赫数的变化规律。选定Ma=30,高度H=60、70和80km,分析化学非平衡效应对气动特性的影响随高度的变化规律。每个状态均计算-16°、-18°、-20°、-22°、-24°和-26°等6个攻角。

图3 “联盟号”返回舱模型Fig. 3 Model of Soyuz re-entry module
2.2化学非平衡下气动特性随马赫数的变化
图4是计算得到的不同来流马赫数下的气动力系数(轴向力系数CA和法向力系数CN)随攻角的变化。完全气体模型的CA和CN都没有随马赫数的增加而发生变化;化学非平衡效应影响下的 CA和CN均高于完全气体模型,且两模型之间的差值随马赫数的增加略有增大。经计算,随着马赫数的增加,两模型的CA差值在小攻角时由1.9%上升至2.3%,大攻角时由3.5%上升至4%,表明高马赫数条件下两模型计算的CA差值增大约0.5%。两模型的CN差值在小攻角时由0.1%上升至3.6%,大攻角时由1.6%上升至4.5%,表明高马赫数条件下两模型计算的CN差值增大约3%。综上,化学非平衡效应的影响程度随马赫数增加得到增强。
图5是计算得到的不同来流马赫数下的返回舱升阻特性(升阻比L/D)和配平特性(俯仰力矩系数CMZ)随攻角的变化。同样,完全气体模型下,不同马赫数的结果一致。化学非平衡效应影响下的L/D和CMZ均大于完全气体模型,且两模型之间的差值随马赫数的增加略有增大,和气动力系数的变化规律一致,说明化学非平衡效应的影响在更大的马赫数下更显著。

图4 H=60km、不同马赫数下轴向力系数和法向力系数随攻角的变化Fig. 4 Axial and normal force coefficients versus α for different Ma at H=60km

图5 H=60km、不同马赫数下升阻比和俯仰力矩系数随攻角的变化Fig. 5 L/D and pitching moment coefficients versus α for different Ma values at H=60km
图6是计算得到的不同来流马赫数下的返回舱压心偏移位置∆xcp随攻角的变化。对于两种气体模型而言,压心变化规律一致。在小攻角时,返回舱压心后移;随着攻角绝对值的增大,压心后移量逐渐减小,在大攻角时变为前移。考虑化学非平衡效应,返回舱压心出现附加前移,且随着马赫数的增大返回舱压心的附加前移量更大。
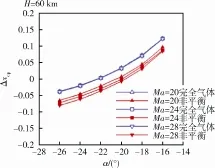
图6 H=60km、不同马赫数下压心偏移位置随攻角的变化Fig. 6 Pressure center offset versus α for different Ma values at H=60km
表3是根据CMZ计算结果得到的返回舱在不同马赫数下的配平攻角αtrim。马赫数增加时,配平攻角的绝对值减小,化学非平衡与完全气体模型的配平攻角差值∆α变大,这同样说明马赫数增加时,化学非平衡的影响增强。

表3 H=60km、不同马赫数下的配平攻角特性Table 3 Trim angles for different Ma values at H=60km
2.3化学非平衡下气动特性随高度的变化
图7是Ma=30、不同高度下计算得到的返回舱气动力系数随攻角的变化。高度变化导致来流密度和温度变化,影响了返回舱头部的激波脱体距离,造成返回舱受力发生变化。图中可见,随着高度的增加,两模型均为CA减小,CN的绝对值减小。经计算,随着高度的增加,两模型间的CA差值在小攻角时由2.6%上升至3.5%,大攻角时由1.3%增大至1.7%;CN差值在小攻角时由0.6%上升至4.6%,大攻角时由2%增大至5%。表明化学非平衡效应的影响程度随高度增加有所加强,与其随马赫数变化的规律近似。
图8是Ma=30、不同高度下计算得到的返回舱升阻特性和配平特性随攻角的变化。不同攻角的升阻比和俯仰力矩系数均随高度增加而增大。两模型间的升阻特性和配平特性差值随高度增加也略有增大。
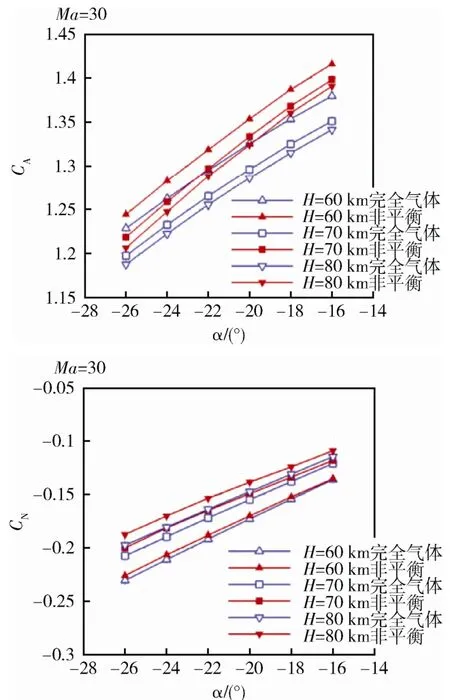
图7 Ma=30、不同高度下轴向力系数和法向力系数随攻角的变化Fig. 7 Axial and normal force coefficients versus α for different altitudes at Ma=30

图8 Ma=30、不同高度下升阻比和俯仰力矩系数随攻角的变化Fig. 8 L/D and pitching moment coefficients versus α for different altitudes at Ma=30
图9是Ma=30、不同高度下计算得到的返回舱压心偏移位置随攻角的变化。化学非平衡效应使压心偏移量增大,且在大攻角时压心偏移量随高度增加而增大的趋势较完全气体更为显著。

图9 Ma=30、不同高度下压心偏移位置随攻角的变化Fig. 9 Pressure center offset versus α for different altitudes at Ma=30
表4是根据CMZ计算值得到的返回舱在不同高度下的配平攻角。可见两模型预测的配平攻角绝对值均随高度增加而减小,且两种模型的配平攻角差值在随高度增加而增大。

表4 Ma=30、不同高度的配平攻角特性Table 4 Trim angles for different altitudes at Ma=30
3 机理分析
3.1马赫数变化下的非平衡效应影响分析
图10是高度60km、攻角-20°时,不同马赫数下的空间和表面的对称面压力系数。结果表明在60km高度下马赫数对激波形状的影响比较小。
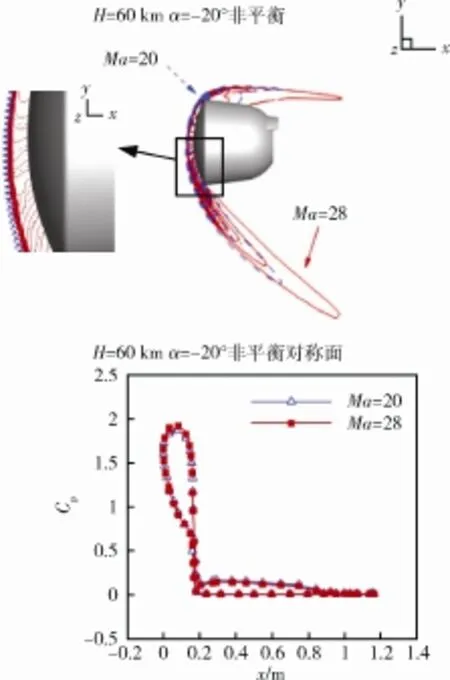
图10 H=60km、α=-20°,不同马赫数下的空间和表面的对称面压力系数Fig. 10 Pressure coefficients in symmetric plane and on the surface for different Ma values and H=60km, α=-20°
高马赫数时激波脱体距离略有减小,造成驻点处压力系数稍高;其他位置的压力系数变化不如驻点处明显,仅可见后体锥身部的迎风区压力系数在低马赫数时略大。
为直观比较低压力区域的压力系数,在返回舱对称面空间选择2个位置进行局部比较,具体位置如图11所示。沿图中所示截线进行空间气流压力的提取,以及不同模型的压力系数比较。
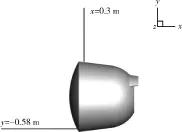
图11 截线位置示意Fig. 11 Schematic diagram of slice lines’ positions
y=-0.58m截线处于头部背风区,气流经过激波压缩后沿返回器表面经历连续膨胀流至此处,较驻点压力明显下降。图12显示:马赫数增大时,完全气体模型压力系数曲线无明显变化,化学非平衡模型压力系数更小,产生附加抬头力矩,究其原因是化学非平衡效应加强了膨胀作用。

图12 H=60km、α=-20°,不同马赫数下的截线压力系数Fig. 12 Pressure coefficients along slice lines for different Ma values at α=-20°, H=60 km
x=0.3m截线处于后体迎风区,经过肩部强膨胀后压力系数进一步降低。马赫数增大时,两模型间的差值更大,使法向力绝对值减小,产生附加抬头力矩。结合驻点处压力升高,可见马赫数增大时,非平衡模型的气体轴向力增大,法向力绝对值减小,配平攻角减小,与计算结果一致。化学非平衡模型的压力曲线在马赫数增大时与完全气体模型间的差值更大,说明马赫数增大对化学非平衡效应的影响有增强作用。
3.2高度变化下的非平衡效应影响分析
图13是Ma=30、攻角-20°时,不同高度下的空间和表面的对称面压力系数。马赫数相同使激波形状基本一致。和变马赫数状态相比,高度变化对压力分布的影响不明显。驻点高压力区压力系数一致,仅在后体迎风区可观察到高空时压力系数略大。

图13 Ma=30、α=-20°,不同高度下的空间和表面的对称面压力系数Fig. 13 Pressure coefficients in symmetric plane and on surface for different altitudes at Ma=30, α=-20°
图14是截线位置的压力系数变化曲线。不同高度下来流温度与密度不同,导致压力分布有小的差异。化学非平衡效应加强了膨胀作用,前体背风面压力系数略小,高度增加时压力系数变化不明显;后体迎风面在高度增加时压力系数略大,和完全气体模型间的差值减小。综合驻点及前体、后体的压力分布,高度变化对轴向力影响不大,法向力系数绝对值减小。高度增加时,仅后体迎风区压力曲线略有不同,造成化学非平衡气体模型的压力分布更加靠近完全气体模型。高度增加时,摩阻的作用愈加显著,对气动特性的影响也更加显现,压力比较可能已无法完全解释气动特性的变化。
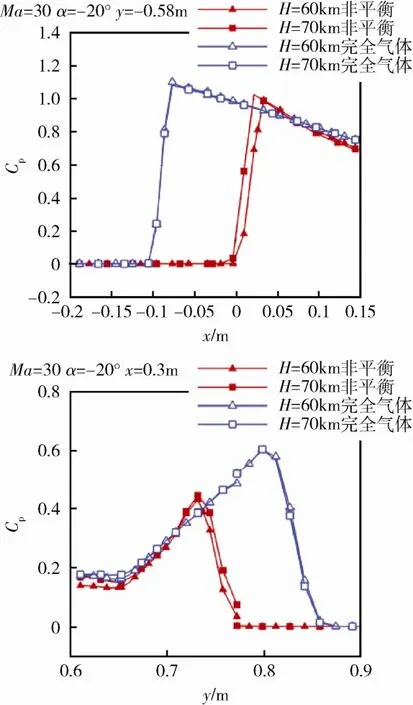
图14 Ma=30、α=-20°,不同高度下的截线压力系数Fig. 14 Pressure coefficients along slice lines for different altitudes at Ma=30, α=-20°
4 结论及建议
通过三维化学非平衡流动的仿真计算,比较了再入返回舱在完全气体模型和化学非平衡气体模型下的流动特征与气动力特性,对其影响机理进行了分析,得到以下结论:
1)高度不变条件下,随着马赫数的增加,完全气体模型气动特性参数基本不变化;而在化学非平衡效应影响下,气动特性参数除法向力系数绝对值小于完全气体模型,其余均高于完全气体模型。对两模型间的参数差值变化规律而言,马赫数增加,轴向力系数差值变化不大,法向力系数和俯仰力矩系数的差值有明显增大。化学非平衡效应造成压心位置偏移量增加。两模型间的配平攻角差值随马赫数增加而增大。这些说明,随马赫数增加,化学非平衡效应对气动特性的影响力增强。
2)保持马赫数不变,随高度的增加,化学非平衡效应影响下的气动特性与完全气体的变化趋势一致。化学非平衡效应影响下的轴向力系数、法向力系数、升阻比和俯仰力矩系数在高度增加时均比完全气体模型的更大。化学非平衡效应使高度增加时返回舱压心位置偏移量更大。两模型间的配平攻角差值在高度增加时也更大。
3)随着飞行高度增加,流动稀薄效应增强,化学反应趋弱,影响气动特性的特征参量向速度和Kn数过渡,且摩阻的作用愈加显著,对气动特性的影响也更加显现。以马赫数和压力作为分析条件和因素略显不足,未来需要在考虑滑移流动的条件下深入研究化学非平衡对摩阻的影响,以理解高空非平衡效应对气动特性的影响规律。
(References)
[1] 吕俊明, 潘宏禄, 苗文博, 等. 化学非平衡效应对返回舱再入气动力特性的影响[J]. 航天返回与遥感, 2014,35(3):11-19 LÜ J M, PAN H L, MIAO W B, et al. Impact of chemical non-equilibrium effect on aerodynamic characteristics of reentry capsules[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(3):11-19
[2] MAUS J R, GRIFFITH B J, SZEMA K Y. Hypersonic Mach number and real gas effects on space shuttle orbiter aerodynamics[J]. Journal of Spacecraft and Rockets, 1984, 21(2):136-141
[3] SHINN J L, MOSS J N, SIMMONDS A L. Viscous-shock-layer heating analysis for the shuttle windward-symmetry plane with surface finite catalytic recombination rates:AIAA 82-0842[R], 1982
[4] SHIGEYA W, SHINJI I, YUKIMITSU Y. Aerodynamic characteristics evaluation of hypersonic flight experiment vehicle based on flight data[J]. Journal of Spacecraft and Rockets, 1997, 34(4):464-470
[5] HOLDEN M S, WADHAMS T P, MACLEAN M, et al. Experimental studies in LENS I and X to evaluate real gas effects on hypervelocity vehicle performance:AIAA 2007-204[R], 2007
[6] PRABHU D K, PAPADOPOULOS P E, DAVIES C B, et al. Shuttle orbiter contingency abort aerodynamics II:real-gas effects and high angles of attack:AIAA 2003-1248[R], 2003
[7] 梁杰, 李志辉, 杜波强. 飞船返回舱再入稀薄流域配平特性研究[J]. 航天返回与遥感, 2013, 34(2):42-48 LIANG J, LI Z H, DU B Q. Research on trim features of reentry capsule in hypersonic rarefied flow regime[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(2):42-48
[8] 詹慧玲, 陈冰雁, 刘周, 等. 典型再入返回器气动特性对比与改进研究[J]. 航天返回与遥感, 2013, 34(6):11-20 ZHAN H L, CHEN B Y, LIU Z, et al. Comparative study and improvement design on aerodynamic characteristics of typical reentry capsules[J]. Spacecraft Recovery &Remote Sensing, 2013, 34(6):11-20
[9] 苗文博, 程晓丽, 艾邦成. 壁面催化条件对热环境预测的影响[J]. 航天器环境工程, 2009, 26(增刊1):45-49
[10] 吕俊明. COIL气动物理与化学过程耦合规律与应用研究[D]. 北京:中国科学院力学研究所, 2009
[11] GNOFFO P A, GUPTA R N, SHINN J L. Conservation equations and physical models for hypersonic air flows in thermal and chemical nonequilibrium:NASA TP-2867[R], 1989
[12] PARK C. Review of chemical-kinetic problems of future NASA missions I:earth entries[J]. Journal of Thermophysics and Heat Transfer, 2015, 7(3):385-398
[13] HILLJE E R. Entry flight aerodynamics from Apollo mission AS-202:NASA TN D-4185[R], 1967
[14] HASSAN B, CANDLER G V, OLYNICK D R. The effect of thermo-chemical nonequilibrium on the aerodynamics of aerobraking vehicles:AIAA 92-2877[R], 1992
(编辑:张艳艳)
The effect of chemical non-equilibrium on aerodynamic characteristics of reentry vehicles
LÜ Junming, CHENG Xiaoli, YU Jijun, HUANG Yuqun
(China Academy of Aerospace Aerodynamics, Beijing 100074, China)
The chemical non-equilibrium has a strong impact on the aerodynamic characteristics of re-entry vehicles flying at high Mach number, which leads to a high temperature shock layer. The altitude and velocity variations would affect the chemical non-equilibrium, and in turn would affect the aerodynamic changes. The numerical investigation and the mechanism analysis are carried out for the re-entry vehicles by solving a three dimensional Navier-Stokes hydrodynamics equation, to understand the effect of the chemical non-equilibrium on the aerodynamic characteristics, as compared to the perfect gas model. The good agreement between the calculated results and the reference data for AS-202 flight test validates the model and the numerical methods. The results show that the predictions of the perfect gas model remain the same and the differences of the aerodynamic forces between the perfect gas model and the chemical reaction gas model are increased with the increase of the Mach number under unchanged altitude. That is because the increase of the Mach number strengthens the chemical non-equilibrium effect. With the increase of the altitude under the same Mach number, the differences between these two gas models show the same trend, the aerodynamic force and the trim angle deviations increase slightly. That indicates the increase of the altitude also strengthens the chemical non-equilibrium effect. It is found that the change of the flow structure under the chemical non-equilibrium and the flucturation of pressure distribution under different flight conditions is the main reason of the aerodynamic variations.
chemical non-equilibrium; re-entry; aerodynamic characteristics; hypersonic; flight conditions
O354.7
A
1673-1379(2016)04-0370-08
10.3969/j.issn.1673-1379.2016.04.006
2016-01-07;
2016-07-11
国家自然科学基金项目(编号:11402251)
吕俊明(1981—),男,博士学位,高级工程师,主要从事高超声速流动和高温气体效应研究。E-mail:junminglyu@foxmail.com。

