混合梁轨道专用斜拉桥自振特性研究

杨继承，李　涛

（招商局重庆交通科研设计院有限公司，重庆　400067）

混合梁轨道专用斜拉桥自振特性研究

杨继承，李涛

（招商局重庆交通科研设计院有限公司，重庆400067）

以国内最大的混合梁轨道专用斜拉桥重庆高家花园大桥为研究对象，应用大型有限元软件建立全桥模型，采用子空间迭代法进行动力分析，得出该桥的自振频率和振型，并在此基础上研究结构参数对桥梁低阶频率和地震响应的影响。计算结果表明：双塔混合梁轨道专用斜拉桥辅助墩的设置对桥梁结构刚度分配十分有限，低阶自振频率及振型影响较小；主梁横向刚度对主梁侧弯的振动频率影响较大；半漂浮体系和固结体系振动频率基本相同，漂浮体系主梁侧弯振动频率较前两者小，且地震作用下结构响应十分显著；主梁及2期恒载对主梁低阶频率和地震响应较为显著，而对索塔的低阶振动频率影响较小。研究成果可为同类斜拉桥的设计及施工提供参考。

混合梁；轨道专用斜拉桥；自振特性；地震响应；参数分析

近年来，混合梁斜拉桥因其跨越能力强、造型美观、经济性好等优点而越来越得到工程界的青睐。目前已建成通车的混合梁斜拉桥有法国诺曼底桥，日本多多罗桥以及中国的武汉白沙洲大桥、塘沽海河大桥、台湾高平大桥等。与钢斜拉桥或者预应力混凝土斜拉桥相比，混合梁斜拉桥既充分发挥了钢材跨越能力大的优势，又充分体现了混凝土材料压重、增加全桥整体刚度和直接参与受力的作用［1-3］。

桥梁结构的自振特性反映了桥梁结构刚度和刚度分布的合理性，是桥梁结构动力分析，桥梁抗风、抗震研究的基础［4-5］。相对一般公路桥梁而言，轨道专用桥具有桥面宽度小、活载较大且动力效应突出的特点，设计时有必要对其进行专门研究。目前，国内外已建混合梁斜拉桥多为公路桥梁，对于混合梁轨道专用斜拉桥的自振特性研究几乎还是一片空白。为此，本文以国内最大的轨道专用斜拉桥重庆高家花园大桥为研究对象，建立有限元模型，对双塔双索面混合梁轨道专用斜拉桥自振特性进行研究，并总结此类桥梁的相关规律，为同类桥梁设计和施工提供参考。

1　工程概况

重庆高家花园轨道专用桥位于轨道环线沙正街站和玉带山站区间，其设计速度为100 km/h，主桥跨度52 m+68 m+340 m+66.5 m+50.5 m。该桥为双塔双索面混合梁斜拉桥，边跨设置辅助墩，整体结构为半漂浮体系。桥面布置为1.0 m（风嘴）+ 1.25 m（拉索区）+15.1 m（车行道+人行道兼检修道）+1.25 m（拉索区）+1.0 m（风嘴），桥梁全宽19.6 m。主桥加劲梁中跨采用正交异性桥面板流线型扁平钢箱梁，桥梁中心线处梁高3 m，边跨混凝土箱梁外轮廓尺寸及拉索的横向布置均与中跨钢箱梁相同，且在轨道线处设置腹板，将箱梁分成单箱3室断面。索塔为钢筋混凝土H型索塔，梁顶面以上设置1道横系梁。斜拉索横向为双索面，立面呈竖琴布置，每个塔肢设置13对斜拉索，塔上拉索间距约6 m，中跨主梁拉索间距12.0 m，边跨主梁拉索间距8.0 m。高家花园大桥桥型总体布置如图1所示。

图1　高家花园大桥桥型布置

2　结构动力特性基本理论

运用达朗贝尔原理对结构各个节点建立如下振动方程式：

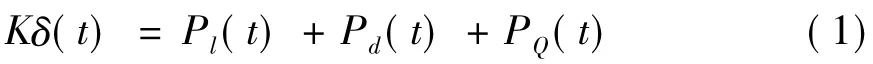
式中：K为结构的整体刚度矩阵；δ（t）为节点位移矢量；Pl（t）为节点惯性力；Pd（t）为节点阻尼力；PQ（t）为节点激振力。

若将每个单元所计算出的由惯性力引起的等效节点荷载集成，则可得到整个梁系统的惯性力节点荷载列阵：

同样，若将每个单元所计算的由阻尼力引起的等效节点荷载集成，则可得到整个梁系统的整体阻尼节点荷载列阵：

将式（2）、（3）代入式（1）可得到如下振动方程式：

令PQ（t）=0可得到自由振动微分方程：

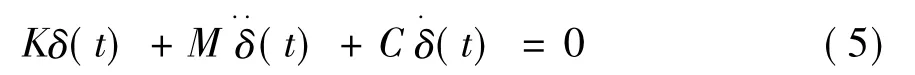
计算桥梁结构动力特性时，因阻尼对其影响很小而忽略不计，故令C=0，可得到结构无阻尼的自由振动微分方程：

由此可得到结构体系非零解的特征方程为：

式中：ω为结构自振频率。

由式（7）可知，求解结构自振频率的问题从而转化为求解方程的广义特征值［3］。由于桥梁结构的复杂性，故一般借助于计算机，采用有限元法进行迭代求解。其中子空间迭代法就是一种收敛速度快、计算精度高的一种方法，也是大型桥梁结构振动分析最有效方法之一［6］。

3　有限元模型建立

笔者应用MIDAS CIVIL大型有限元软件对高家花园大桥进行模拟，结构由索塔、桥墩、桩基、主梁、拉索组成。根据结构自身特点，全桥共建立1051个节点，882个单元，结构离散如图2所示。其中，索塔、桥墩、主梁采用计入剪切变形对结构内力与位移影响的空间杆单元，斜拉索采用只受拉桁架单元，每根拉索对应1个单元。

边界条件设置：辅助墩、过渡墩墩底采用固定约束，限制了6个方向自由度；主塔塔底桩基根据地质勘察实测参数，采用土弹簧进行模拟；斜拉索与索塔、主梁的连接均采用无质量的刚臂单元；塔梁、塔墩连接根据选取的支座实际参数按弹性连接进行模拟；荷载主要按照梁单元荷载或节点荷载进行施加。

图2　高家花园大桥结构离散图

4　自振特性分析结果

桥梁的自振特性包括自振频率和振型，其反映桥梁结构刚度及刚度的分布。在合理确定斜拉桥成桥状态的基础上，对高家花园大桥采用子空间迭代法计算结构的自振频率及振型。高家花园大桥模态频率计算结果见表1。

表1　高家花园大桥模态频率

从表1可以看出，高家花园大桥第1、2阶频率较为接近，且第1、2阶频率均为索塔侧弯，振型侧向位移较大。第3阶频率为主梁1阶竖弯。第4阶频率为主梁横向1阶侧弯，反映出轨道专用桥桥面宽度较小引起的横向刚度问题，需引起重视。第6～12阶频率主要表现为高阶的主梁竖弯、主梁侧弯及主梁与塔墩的扭转组合。高家花园大桥前5阶振型如图3所示。

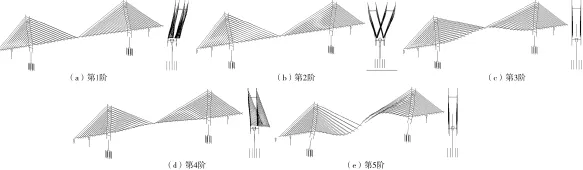
图3　高家花园大桥第1～5阶振型

5　自振特性的影响因素

为了充分认识混合梁轨道专用桥自振特性的影响因素，笔者从辅助墩的设置、主梁竖向刚度及横向刚度、塔梁连接形式、主梁及2期恒载等方面入手，对此类桥梁低阶自振频率及振型分布情况进行研究［7-8］。

5.1辅助墩设置

为了研究辅助墩的设置对混合梁斜拉桥自振特性的影响，本文将对以下3种辅助墩设置情况进行对比：1）不设辅助墩；2）设置一个辅助墩（原模型）；3）设置2个辅助墩（原模型基础上再增设1个）。具体计算结果见表2。

分析表2数据可知，因混合梁斜拉桥边跨混凝土梁刚度相对中跨钢箱梁大得多，辅助墩的设置对桥梁结构刚度分配影响十分有限，且对低阶自振频率及振型影响较小。

5.2主梁竖向刚度及横向刚度

轨道桥梁所受竖向荷载大，横向宽度窄，且受列车摇摆力、离心力和风力的影响，往往影响行车安全性及乘坐舒适度，因此，在结构动力响应分析前有必要就主梁横向刚度和竖向刚度对其自振特性的影响进行研究。下面将以高家花园大桥为例，分析其主梁竖向和横向刚度±10%变化对其自振特性的影响。高家花园大桥主梁刚度对其低阶频率影响情况见表3。

由表3数据可知，主梁竖向刚度的变化对索塔侧弯及主梁竖弯影响均较小，而横向刚度变化对主梁1阶侧弯影响较大。因此，桥梁设计时，主梁侧弯低阶频率可通过横断面优化进行适当调整。

5.3塔梁连接形式

斜拉桥按照主梁的受力状态分为漂浮体系、半漂浮体系、塔梁固结体系和刚构体系，不同体系下结构的静力、动力性能差异大。为研究轨道专用斜拉桥的动力特性，笔者以高家花园大桥为例，分别对漂浮体系（塔墩固结、塔梁分离）、半漂浮体系（塔墩固结、主梁在塔墩处设支撑）和刚构体系（塔、墩、梁固结）的自振特性进行计算分析和比较，计算结果见表4。

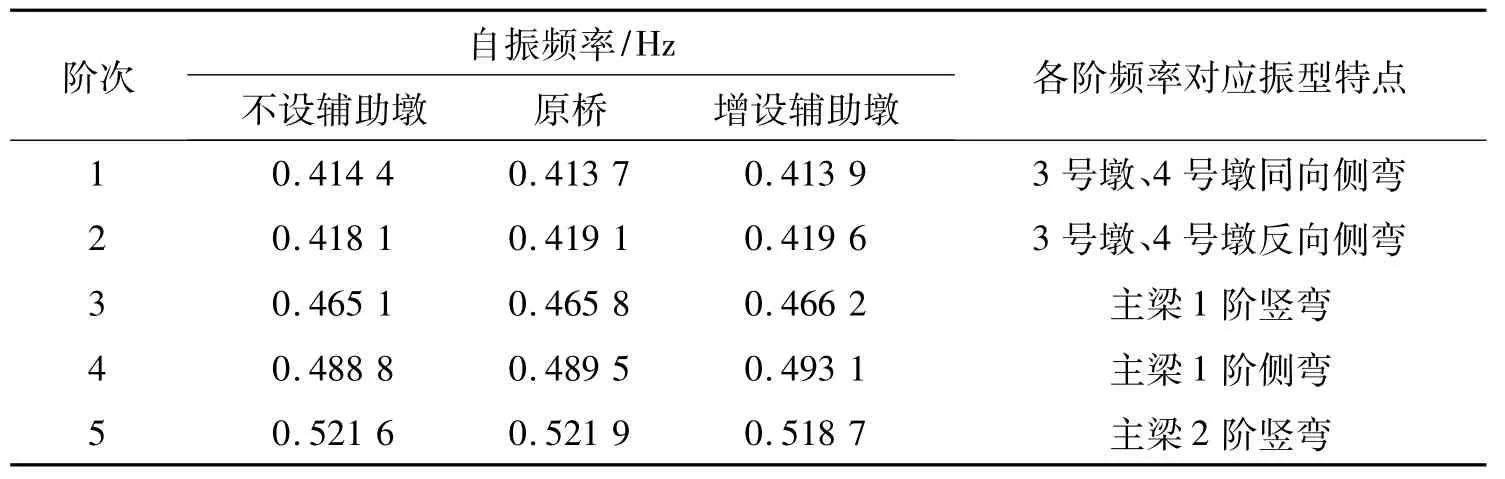
表2　辅助墩设置对低阶频率影响

表3　主梁刚度对低阶频率影响

表4　不同结构体系低阶频率比较

由表4数据可知，混合梁轨道专用斜拉桥半漂浮体系和刚构体系自振频率及振型特点基本相同，而漂浮体系自振频率和振型特点与前两者存在显著差异，尤其是主梁的侧向弯曲由半漂浮体系的4阶频率转化为结构的1阶频率，且频率值减少超过40%。

5.4主梁及2期恒载

为研究桥梁结构自振频率受主梁及2期恒载影响敏感程度，下面以高家花园大桥为例，将自重及2期恒载增加或减少10%，对比桥梁的低阶频率变化情况。计算结果见表5。

由表5数据可知，主梁及2期恒载变化对主梁低阶频率影响较为显著，而对索塔振动低阶频率影响较小。

6　结构参数对结构动力性能的影响

斜拉桥自振特性的研究为桥梁的动力分析提供了理论基础，而通过动力学分析则可更加直观地揭示桥梁结构在外荷载作用下的结构响应。根据上述自振特性影响分析结果，选取对动力特性影响较大的主梁刚度和塔梁连接形式进行动力性能研究。本文以高家花园大桥为例，采用反应谱方法分析桥梁结构在E1和E2地震作用下的响应，对比分析其对参数敏感的影响程度。

6.1主梁刚度

以高家花园大桥主梁刚度参数为基准，分别考虑主梁刚度变化±10%，计算索塔纵横向弯矩和主梁跨中位移，计算结果见表6。

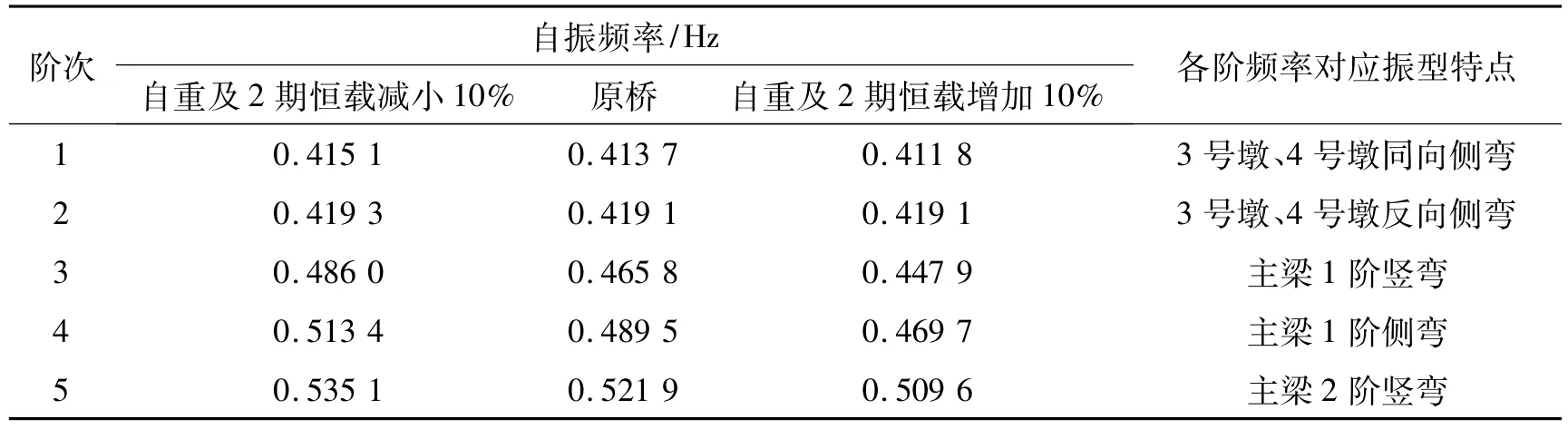
表5　主梁及2期恒载对自振频率影响

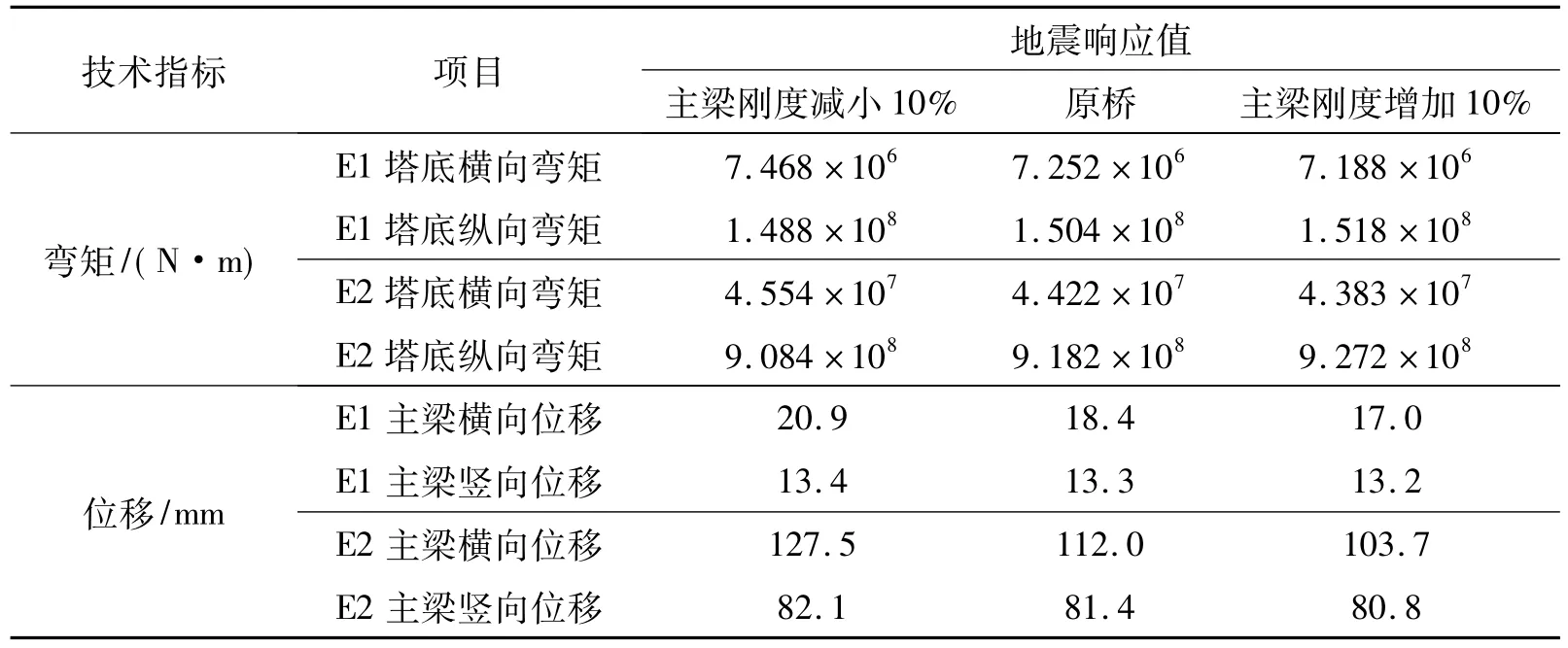
表6　不同主梁刚度地震响应对比

从表6数据可以看出，主梁横向刚度变化10%后，在E1、E2地震作用下索塔塔底横桥向弯矩最大影响约3%，横向位移最大影响约13.8%；索塔纵向弯矩、竖向位移影响均较小。

6.2塔梁连接形式

分析自振特性影响因素可知，漂浮体系与半漂浮体系、固结体系自振特性存在显著差异，而半漂浮体系与固结体系较为接近。因此，结构动力响应分析对漂浮体系和半漂浮体系进行计算和对比，计算结果见表7。

由表7数据可知，E1、E2地震作用下，漂浮体系斜拉桥索塔塔底横向弯矩为半漂浮体系的1.5倍，主梁横向位移漂浮体系约为半漂浮体系的3倍，相差十分显著。而二者索塔纵向弯矩、主梁竖向位移相差均较小。

6.3主梁及2期恒载

为验证主梁及2期恒载对动力性能的影响程度，笔者在高家花园大桥原桥基础上按增减10%的幅度进行计算，得到索塔塔底弯矩和主梁位移，见表8。

由表8数据可知，主梁及2期恒载变化10%后，E1、E2地震作用下索塔横向弯矩、主梁横向位移变化约10%，纵向弯矩变化约3%，竖向位移变化相对较小。

表7　塔梁连接形式地震响应对比

表8　不同主梁及2期恒载地震响应对比

7　结论

本文基于结构动力学的基本理论，在分析混合梁轨道专用桥自振特性的基础上，对影响桥梁自振特性和地震响应的结构参数进行研究，并得出如下结论：

1）辅助墩的设置对双塔混合梁轨道专用斜拉桥低阶自振频率的影响较小。主梁竖向刚度对索塔侧弯及主梁竖弯的振动频率影响较小，而主梁横向刚度对主梁侧弯的振动频率影响较大。

2）双塔混合梁轨道斜拉桥半漂浮体系和固结体系振动频率基本相同，漂浮体系与前两者存在显著差异，主梁侧弯往往容易成为结构的基频。

3）主梁自重及2期恒载对主梁低阶频率影响较为显著，对索塔低阶振动频率的影响较小。

4）E1、E2地震作用下，主梁横向刚度、主梁及2期恒载对主梁横向位移影响较大。结构体系对索塔塔底弯矩、主梁位移的影响十分显著，其中塔底横向弯矩漂浮体系为半漂浮体系的1.5倍，横向位移超过3倍。因轨道桥对主梁横向位移要求较高，故设计应尽量避免采用漂浮体系。

［1］ 林元培.斜拉桥［M］.北京：人民交通出版社，2004.

［2］刘士林，王世舜.斜拉桥设计［M］.北京：人民交通出版社，2004.

［3］ 李国豪.桥梁结构稳定与振动［M］.北京：中国铁道出版社，2002.

［4］李小珍，强士中.大跨度公铁两用斜拉桥车桥动力分析［J］.振动与冲击，2003，22（1）：6-26.

［5］徐永胜.某三塔斜拉桥动力特性分析［J］.城市道桥与防洪，2009（5）：64-66.

［6］高飞，陈淮，杨磊，等.部分斜拉桥力学性能分析［J］.郑州大学学报（工学版），2005，26（1）：54-56.

［7］王刚，曹雪琴.高速铁路大跨度斜拉桥车桥动力分析［J］.上海铁道大学学报，2000，21（8）：7-21.

［8］邓志荣，李传习.江西九江长江公路斜拉桥动力特性分析［J］.公路与汽运，2010（3）：118-121.

Study on Self Vibration Characteristics of Special Cable Stayed Bridge for Mixed Beam Track

YANG Jicheng，LI Tao

This paper，taking the largest rail-only mixed-beam cable stayed bridge in China，Chongqing Gaojia Huayuan Bridge as study object，uses large scale finite element software to set up a whole bridge model and subspace iterative method for dynamic analysis to obtain the self vibrating frequency and vibrating type of this bridge.Based on this，this paper studied the influence of structural parameters to bridge low order frequency and seismic response.Calculation results show that the arrangement of auxiliary piers in twin-tower rail-only mixed beam cable stayed bridge track has quite limited influence on the distribution of bridge structural stiffness and has relatively small influence to low order self vibrating frequency and vibrating type.The lateral stiffness of main beam has greater influence to vibrating frequency of the side bending of main beam.The vibrating frequency of half-floating system and fixed system is similar，while the main beam side bending vibrating frequency of floating system is smaller than the former two，and the structural response under earthquake is quite significant.The main beam and phase 2 constant load has obvious response to main beam low order frequency and earthquake，while it has relatively small influence to low order vibrating frequency of the cable tower.The results may be used as reference for similar cable stayed bridge design and construction.

Mixed beam；rail-only cable stayed bridge；self vibrating characteristics；seismic response；parameter analysis

1009-6477（2016）04-0049-06

U448.27

A

10.13607/j.cnki.gljt.2016.04.011

重庆市科委应用开发项目（cstc2015yykfA0002）

2016-03-16

杨继承（1986-），男，重庆市人，硕士研究生，工程师。