星载稀疏相控阵天线的多目标优化设计

刘 恒，赵宏伟，刘 波

（西安空间无线电技术研究所 陕西 西安　710100）

星载稀疏相控阵天线的多目标优化设计

刘 恒，赵宏伟，刘 波

（西安空间无线电技术研究所 陕西 西安710100）

针对星载相控阵天线高增益、低副瓣的设计要求，提出了对星载六边形相控阵天线进行稀疏布阵的方法。根据需求建立了星载相控阵天线高增益、低副瓣的两目标的优化模型，使用NASA-II算法对其进行多目标设计优化。为了快速计算六边形天线阵的方向图，通过在孔径中添加虚拟阵元把六边形阵列转化为可以实现二维傅里叶变换的矩形阵列，大大节省了算法优化时间。结果表明，星载稀疏相控阵天线多目标优化思路和方法在工程应用中的有效性和合理性，为设计者提供了多种可行的选择方案。

稀疏阵列；相控阵天线；FFT；NASA-II算法

星载稀疏相控阵天线是指从一个阵元周期分布的阵列中去除掉一些天线阵元，或者把这些阵元连接到匹配负载上。既可以减少阵列天线成本和重量，还可以获得与满阵排布相当的窄波束，当阵元均匀激励时，稀疏阵列天线可以获得比满阵布置更低的副瓣电平［1］。在过去几十年中，稀疏相控阵天线的研究一直是一项重要和有意义的工作。由于在同等阵元间距下，六边形相控阵天线在扫描时比矩形栅格阵列出现栅瓣的时间更晚；且在等幅激励时近似圆形的六边形平面相控阵能够获得相对低的副瓣电平，因此六边形相控阵天线阵被广泛应用在卫星通信中［2-3］。在星载稀疏相控阵天线设计中，希望主瓣增益尽可能的高而副瓣电平尽可能的低，同时最大副瓣电平和主瓣增益分别低于和高于某一给定的约束值。因此，星载稀疏相控阵天线的设计是典型的多目标优化问题。

随着计算机技术的发展，高效的稀疏阵列优化算法已成研究热点，主要有遗传算法［4-5］、粒子群算法［6-7］、进化差分算法［8-9］、蚁群算法［10］等各种优化算法的混合算法［11-12］。各种智能进化优化算法。在这些文献中通常把多个目标函数通过不同的加权权重构造成单个目标函数进行优化。在实际设计中，权重的分配及单目标函数构造方式带有很强的主观性，而决策者往往需要多种可供选择的方案进行比较，就需要不断的修改权重及单目标函数进行很多次优化。在多目标优化中，各目标之间无法比较，存在冲突，导致不存在对所有目标函数都是最优解。Goldberg将Pareto知识［13］引入进化算法中来解决多目标优化问题的新思路之后，越来越多学者们提出了基于Pareto支配关系的进化算法，使之成为求解多目标优化问题的一种趋势。其中以非支配遗传算法（NSGA-II）［14］最具有代表性。

本文应用NSGA-II算法对卫星上广泛应用的正三角形排列的六边形平面相控阵天线进行稀疏布阵优化，以达到高增益、低副瓣的辐射特性。首先利用六边形阵列的几何对称阵性确定了六边形平面相控阵天线中的独立单元数，实现对大型六边形相控阵天线优化变量进行降维。并根据六边形阵列的排列特征，通过在阵列中添加虚拟单元的方式把六边形转换为矩形阵列，从而利用FFT快速计算阵列方向图。然后建立了增益和峰值副瓣电平两目标优化模型的解析表达式。利用NASA-II算法对1027个单元（L=18）的六边形相控阵天线进行多目标优化设计，以降低阵列天线的峰值副瓣电平、增高主瓣增益为目的，得到了最优解集的Pareto前端，取得了满意的结果。说明了星载稀疏相控阵天线多目标优化思路和方法在工程应用中的合理性和有效性，为设计者提供了多种可行的选择方案。

1　星载相控阵天线模型

1.1六边形天线方向图

星载六边形相控阵天线的几何结构如图1所示，它是由按等边三角形排列的天线单元组成。可以看出六边形平面相控阵天线是由若干行横向等间距的直线阵在纵向交替紧密排布组成，其每行的单元数量随着远离中心行依次递减。对于一个由L个同心六边形环阵组成六边形天线，其第一行的单元数为L+1个；随着行数的增加，每行的单元数依次增一个，到L+1行的单元数增加到最多的2L+1个；再随着行数继续增加，每行的单元数则依次减少一个，到2L+1行的单元数减少到L+1个。下面将利用六边形平面天线阵的这一结构特性推导它的辐射方向图的解析表达式。

图1　六边形平面阵列天线结构图

图2　可见空间区域示意图

由于六边形相控阵天线的每行在y方向是交替排布的，如果通过在每行单元中间添加一个虚拟“单元”，这样就把六边形平面阵列变换为矩形栅格的平面阵列。每行沿x轴方向间距dx=0.5d，每列沿y轴方向间距dy=0.5d·tan60°，d为正三角形排列的单元间距。根据六边形平面阵列的结构和添加的虚拟单元的位置可知，对于一个由L个同心六边形环阵通过在每一行单元中间添加虚拟单元变化为一个2L+1行4L+1列的矩形栅格平面阵。由阵列天线理论可知，在不考虑互耦的情况下，辐射单元为理想点源，六边形阵列方向图满足乘积定理可以表示为：

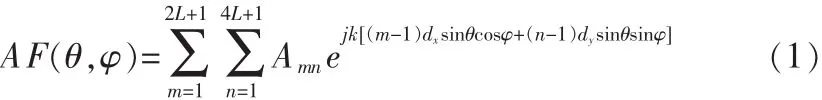
式中：L为同心六边形环阵的数量，k为波数，θ，φ分别为球坐标系的下俯仰角和方位角，Amn是第（m，n）个阵元激励幅度。为了方便，把由M×N个阵元激励组成的矩阵记着A，对于矩阵A与六边形平面阵列不匹配的点，如添加的虚拟阵元和位于六边形阵列孔径外的点，其激励幅度Amn=0。对于与阵列匹配的点，在稀疏优化过程中，当Amn=1，表示单元在工作；当Amn=0，表示单元被剔除。一个由L个同心六边形环阵组成六边形平面天线阵的单元总数可由下式确定：

由于大型六边形阵列天线单元数成百上千，而智能进化算法在对优化变量超过200个的时候，效果变的不太理想，因此需要对六边形阵列天线独立单元进行降维。根据对称性，总共有6个对称轴，位于对称轴上的阵元有6个对称阵元，而非对称轴上的阵元有12个对称阵元。在阵列稀疏优化过程中如果某一个阵元被选定剔除，则与其对称的所有的阵元都将剔除。如图1所示位于图中P标记和y轴的30°扇形区内的单元为该天线阵的独立单元。一个具有L个同心六边形环阵的六边形相控阵天线的独立单元数可由下式计算，其中int（·）为取整函数。

1.2方向图与FFT的关系

由于在进化过程中要反复计算方向图函数的采样点来评估个体的优劣，如果能将降低计算方向图的时间就能够减少评估个体的时间，从而大大提高计算速度。设一个辐射阵元为理想点源，沿x轴方向的阵元间距为dx，y轴方向的阵元间距为dy的M×N元平面阵，在不考虑互耦的情况下，阵列方向图满足乘积定理可以表示为：

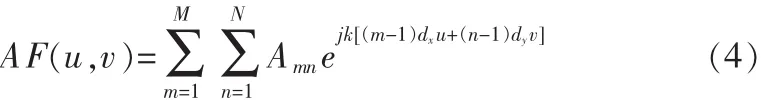
式中：Amn是第（m，n）个阵元激励幅度，k=2π/λ，λ为自由空间波长，u=sinθcosφ，v=sinθsinφ是方向余弦，θ，φ分别为球坐标系的下俯仰角和方位角。令p=Mkdxu/2π+1，q=Nkdyv/2π+ 1，则式（4）变换为

由式 （4）可以看出阵因子AF与阵元激励A之间存在IFFT关系AF=MN×IFFT（A），这样根据具体的问题，将（θ，φ）域的方向图特性映射到（p，q）域中，就可以在（p，q）进行优化。

由u=sinθcosφ，v=sinθsinφ可得u2+v2=sin2θ≤1，在u，v坐标系下，可见区域与一圆区域相对应。对于不同间距的平面阵列，利用二维FFT计算出方向图的可见区域如图2所示。当dx≤λ/2，dy≤λ/2时，可见区域为半径为1的圆A；当dx＞λ/2，dy＜λ/2时，可见区域为半径为1的圆与矩形D的交集；当dx＜λ/2，dy＞λ/2时，可见区域为半径为1的圆与矩形C的交集；当dx＞λ/2，dy＞λ/2时，可见区域为矩形C与矩形D的交集。

1.3目标函数及约束

星载相控阵天线为了得到高增益低副瓣的辐射特性，稀疏布阵综合优化的两个目标函数为最大副瓣电平MSLL与主瓣点的增益G。

其中，x为待优化的相控阵天线独立单元的状态，η为天线的效率，MSLL和D分别为阵列结构x计算得到的最大副瓣电平和最大方向系数。u0=sinθ0cosφ0，v0=sinθ0sinφ0是主瓣点（θ0，φ0）的方向余弦。二重积分的可视空间为u2+v2≤1。考虑到实际需求，通常最大副瓣电平低于SLLmax=-20 dB，所以约束条件g（x）=MSLL-SLLmax＜0。

2　多目标优化设计

对于带约束的多目标优化问题，其数学上可以表示为：

其中F（x）为目标函数，g（x）为约束函数，n和k分别为目标函数和约束函数的个数。多目标优化问题是一个解的集合，这些解在全部目标函数而言是无法比较优劣的，其特点是无法在改进任何目标函数的同时不削弱至少一个其他目标函数，这些解的集合称为Pareto非支配解集合。

2.1Pareto最优解排序

在单目标优化算法中，两个解的优劣程度可以通过他们的唯一适应度值大小确定。在多目标优化算法中，所有的目标函数是同样的重要的，即在优化过程中不能为了改善某些目标函数而恶化其他任何一个目标函数。设x1，x2是所描述的多目标问题的解，当下列条件成立时称x1限制性支配x2，也称与x2相比，x1是Pareto占优。

1）x1属于可行解而不属于x2。

2）x1和x2都不属于可行解且在约束函数 gi（x1）≤gi（x2）（i=1，2，…，k）。

3）x1和 x2都属于可行解且在目标函数Fi（x1）≤Fi（x2）（i=1，2，…，m）。

对于多目标优化的非支配解，经过非支配排序和拥挤度计算［14］，种群中的每个个体i都有两个属性；非支配序 irank和拥挤度idistance。判断种群中任意两个个体优劣的标准为，如果两个个体非支配序不同，非支配序小的更优；如果两个个体的非支配序相同，则拥挤度较大的个体更优。

2.2NSGA-II算法

将进化算法与Pareto概论结合，发展出很多基于Pareto最优概论的多目标进化算法，其中具有代表性的是NSGAII。由于NSGA-II在对稀疏相控阵天线进行优化的时可以直接进行二进制编码，不需要进行编码处理，是稀疏相控阵天线多目标优化的最佳工具。本文直接采用的文献［14］的二进制编码NSGA-II算法。由于多目标优化中非支配解的优劣无法判断，因此进化后的种群规模会增加，经过交叉、变异后的NP个子代与NP个父代混合进行非支配排序，种群规模在进化后增加为2NP，然后通过非支配排和拥挤度排序后选择前NP个个体进入下一代。根据以上策略，NSGA-II算法步骤如下：

1）初始化种群，生成种群规模为NP个父代。

2）计算种群中每个个体的目标函数值和约束函数值。

3）通过遗传算法的交叉、变异生成群规模为NP个子代。

4）计算子代的目标函数及约束函数。

5）对父代和子代混合的2NP个个体进行非支配排序，选出前NP个性能最佳的个体。

6）从步骤3）重复直至满足迭代结束条件。

3　实例分析

在实际应用中，经过计算和分析，我们取种群规模NP等于二进制序列长度的二倍。阵元间距d=λ/2，二维IFFT运算采样点数K×K=512×512。NSGA-II算法参数的选择使用文献［15］推荐的。单点交叉，交叉概率取0.9，变异概率取0.01，进化代数取5000次。假设天线的效率η=1，则增益G等于方向性系数D，以由1027个单元（L=18）的六边形相控阵天线为例进行优化实例。

图3　Pareto最优解集前端分布

图3给出了在5 000次两目标函数评价后，1 027个单元的组成六边形平面相控阵天线稀疏布阵的Pareto最优解集前端分布。可以看出峰值副瓣电平下限为 （-27.8 dB，33.2 dB），约束的上限为（-20 dB，34.1 dB）。图4和图5分别给出了峰值副瓣电平上限和下线的孔径阵元分布和归一化远场方向图，其可视空间为u2+v2≤1。可以看出，优化得到的六边形稀疏阵列符合阵列优化规律，即在优化阵列中，阵元的稀疏总是发生在阵列边缘，而阵列中心的阵元一般不会被稀疏掉。

表给出了从求解得到的Pareto最优解中选择4个最优解对应的变量值以及对应的目标函数值。其中包括两个边界点和两个中间点。表格中的数据表明，峰值副瓣电平PSLL最低为-27.8 dB，方向性系数达到最小值33.2 dB，而当PSLL最高为-20 dB，方向性系数达到最大值34.1 dB，这两个目标函数不能同时取得最优值。说明在星载相控阵天线优化设计中，最大副瓣电平和增益确实是一组存在矛盾的目标，适合用多目标优化方法求解这类问题。相对于单目标优化算法，采用多目标方法能从多个不同的角度提供不同的最优解，为决策者提供更多的指导信息和帮助。

图4　方向性系数最好的解

图5　峰值副瓣电平最好的解

表1　最优集合中4个最优解对应的优化结果

4　结　论

文中以星载稀疏相控阵天线优化布阵为研究对象，采用多目标优化算法，将阵列的优化布阵转化为多目标优化的数学问题。为了降低大型六边形阵列的优化变量维数，通过对阵列中对称的单元进行等效处理，独立单元数降低为阵列单元的十分之一。同时把六边形阵列转化为可以实现二维傅里叶变换的矩形阵列模型，使计算量成倍减少，也可用于解决其他种类的矩形阵和三角阵平面阵列天线的稀疏布阵优化，具有很好工程实用价值，为大型阵列天线的稀疏优化提供了有效途径。星载天线的高增益、低副瓣为优化目标，充分体现了星载稀疏相控阵天线多目标优化思路和方法的合理性和有效性，为决策者提供了多种可行的选择方案，未来可考虑更多的目标及约束进行进一步的应用研究。

［1］W.P.M.N.Keizer.Synthesis of Thinned planar circular and square Arrays using density tapering［J］.IEEE Transactions on Antennas and Propagation，2014，62（4）：1555-1563.

［2］Dietrich F J，Metzen P，Monte P.The Globalstar Cellular satellite system［J］.IEEE trans on Antennas，1998，46（6）：935-942.

［3］李东风，龚中麟.六边形平面天线阵优化稀疏布阵研究［J］.电子学报，2002，30（3）：376-380.

［4］Haupt R L.Thinned arrays using genetic algorithms［J］.IEEE Transactions on Antennas and Propagation，1994，42（7）：993-999.

［5］王玲玲，方大纲.运用遗传算法综合稀疏阵列［J］.电子学报，2003，31（12A）：2135-2138.

［6］N.Jin，Y.Rahmat-Samii.Advances in particle swarm optimization for antenna design：real-number，binary，singleobjective and multiple objective implementations［J］.IEEE Trans on Antennas and Propagation，2007（55）：556-567.

［7］M.Donelli，A.Martini，A.Massa.A hybrid approach based on PSO and Hadamard difference sets for the synthesis of square thinned arrays［J］.IEEE Trans on Antennas and Propagation，2009，57：2491-2495.

［8］D.G.Kurup，M.Himdi，A.Rydbery，Synthesis of uniform amplitude unequally spaced arrays using the differential evolution algorithm［J］.IEEE Trans on Antennas and Propagation，2003，51：2210-2217.

［9］L.Zhang，Y C Jiao，Z B Weng，F S Zhang.Design of planar thinnedarraysusingaBooleandifferentialevolution algorithm［J］.IET Microwaves，Antennas&Propagation，2010，4（12）：2172-2178.

［10］Ó.Quevedo-Teruel，E.Rajo-Iglesias，Ant colony optimization in thinned array synthesis with minimum sidelobe level，IEEE Antennas Wireless Propagation Letters，2006，5：349-352.

［11］Leonardo F.Yepes，David H.Convarrubias，Miguel A. Alonso，et al.Hybrid Sparse Linear Array Synthesis Applied to Phased Antenna Arrays［J］.IEEE Antenna and Wireless Propagation Letters，2014（13）：185-188.

［12］OvidioMarioBucci，StefanoPerna，DanielePinchera. Synthesis of Isophoric Sparse Array Allowing Zoomable Beams and Arbitrary Coverage in Satellite Communications ［J］.IEEETransactionsonAntennasandPropagation，2015，63（4）：1445-1457.

［13］Goldberg D E.Genetic Algorithm in Search，Optimization and Machine Learning.Boston，MA，USA：Addison-Wesley Longman Publishing Co.，Inc.，1989.

［14］K.Deb，A.Pratap，S.Agarwal，T.Meyarivan，A fast and elitist multiobjective genetic algorithm：NSGA-II［J］.IEEE trans on Evol.Comput.，2002，6（2）：182-197.

［15］Pareto Optimization Microwave Filter Design Using Multiobjective Differential Evolution［J］.IEEE Trans.Antenna propagation，2010，58（1）：132-142.

Multi-objective design optimization of satellite thinned array antenna

LIU Heng，ZHAO Hong-wei，LIU Bo
（China Academy of Space Technology（Xi'an），Xi'an 710100，China）

Considering the design purpose of high gain，low side lobes satellite phased array antennas，a thinning process is proposed for hexagonal array.The two objective optimization modes of high gain and low side lobes of satellite antenna are set up according to the requirements.And the NASA-II is applied at this two objective design optimization.Virtual elements are added in the array for translating the hexagon to rectangle which could be convenient to calculate the array factor of hexagon by using the FFT.The simulated results show that the availability and rationality of the multi objective optimization in the satellite thinned phased array antenna，and it could offer several feasible scheme for the designer.

thinned array；phased array antenna；fast fourier transform algorithm；NASA-algorithm

TN959

A

1674－6236（2016）09-0122-04

2015-11-23稿件编号：201511212

国家自然科学基金（61201089）；国家重点实验室基金（9140C530101130C53013）

刘 恒（1986—），男，湖南耒阳人，博士。研究方向：阵列天线优化与设计。