基于固有应变法的桅杆焊接工艺仿真

胡掌稳，熊逸群，牟　军，王海博，郑　轩，胡凌云，庞红良，黄　玉，张　龙

(1.北京市三一重机有限公司，北京 102206；2.北京翔博科技股份有限公司，北京 100086)



基于固有应变法的桅杆焊接工艺仿真

胡掌稳1，熊逸群1，牟军1，王海博1，郑轩2，胡凌云2，庞红良2，黄玉2，张龙2

(1.北京市三一重机有限公司，北京 102206；2.北京翔博科技股份有限公司，北京 100086)

桅杆的材料为Q345B，通过采用焊接的方式，将桅杆的底板、侧板、顶板和加强筋焊接成装配件。桅杆在焊后存在变形，需要通过热校形来减小和控制变形量。基于固有应变法对桅杆的焊接成型工艺进行仿真，通过三维弹塑性有限元仿真，得到焊接成型过程中焊缝周围的残余应力分布和固有应变分布趋势，进而通过固有应变法获得桅杆焊后的整体变形。

焊接；桅杆；固有应变法；三维弹塑性有限元；焊缝应力应变分布

焊接过程中经历了复杂的物理过程，如微观组织、热和力学场量耦合[1-2]。冷却过程积累的塑性应变主要决定了焊接残余变形。桅杆焊接工艺的仿真方法为固有应变法[3-4]。固有应变法的基本原理为先通过热弹塑性有限元法分析焊接接头，得到焊缝周围的残余应力分布和固有应变分布，再将焊缝及其附近所产生的固有应变作为初始应变，进行一次弹性有限元计算，来获得整个桅杆结构的焊接变形，进而优化大型复杂结构的焊接顺序。

北京翔博科技股份有限公司在ABAQUS成熟商用软件的基础上进行封装，基于固有应变法形成了多工艺连续仿真软件焊接工艺模块，实现了大型复杂结构的焊接工艺仿真，可对复杂结构的焊后整体变形进行分析。

1　建立桅杆有限元模型

以SR150型号桅杆为例，采用ABAQUS有限元软件前处理建立的3D几何模型如图1所示[5-6]。采用四面体单元划分网格，网格模型如图2所示。将桅杆放在平台上进行焊接装配，约束桅杆的刚体位移。桅杆实际的焊接工艺参数如下：焊接电流260 A；焊接电压27 V；焊接速度25 m/h；电弧热效率0.75。

图1　桅杆几何模型　　　图2　桅杆网格模型

2　焊接接头三维弹塑性有限元仿真

在桅杆焊接过程中，焊接接头包括对接接头、T型接头和角接接头[7]。采用的热源模型为高斯热源。高斯热源分布计算公式如下[8-9]：

(1)

式中，R为电弧有效加热半径；r为焊接件上任意点至电弧加热斑点中心的距离；η为电弧热效率；U为焊接电压；I为焊接电流。

2.1对接接头仿真结果

对接接头的应力分布如图3～图5所示。由图3～图5得知，焊后在焊缝周围的应力值较大，远离焊缝的区域应力值较小，焊接残余应力主要集中在焊缝及其附近。

图3　对接接头等效应力云图

图4　对接接头最大主应力云图

图5　对接接头最小主应力云图

对接接头的应变分布结果如图6～图8所示。由图6～图8得知，焊后在焊缝周围的应变值较大，远离焊缝的区域应变值较小。 取焊缝横截面，可计算得出焊缝横截面的平均固有应变。通过坐标轴方向得知，PE11为横向固有应变，PE22为纵向固有应变。

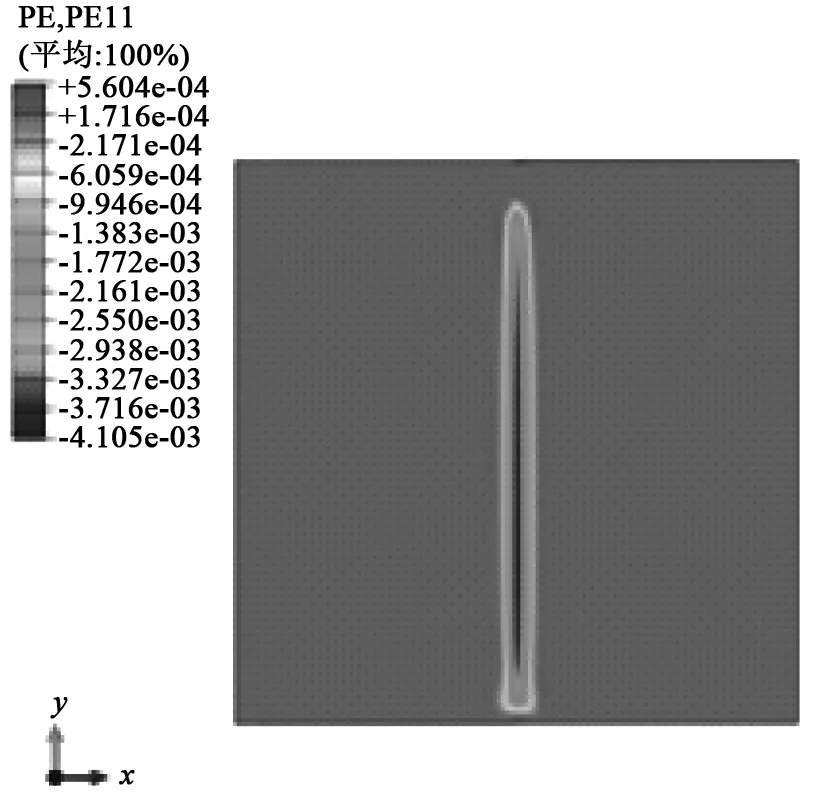
图6　对接接头X方向应变云图

图7　对接接头Y方向应变云图

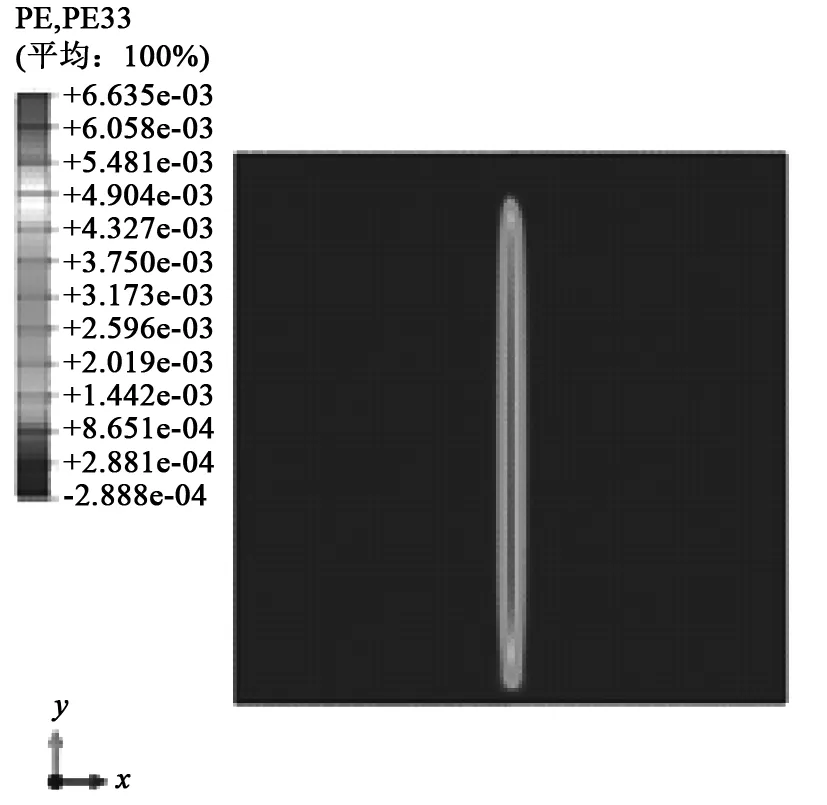
图8　对接接头Z方向应变云图

2.2T型接头仿真结果

T型接头的应力分布如图9～图11所示。由图9～图11得知，焊后在焊缝周围的应力值较大，远离焊缝的区域应力值较小，焊接残余应力主要集中在焊缝及其附近。

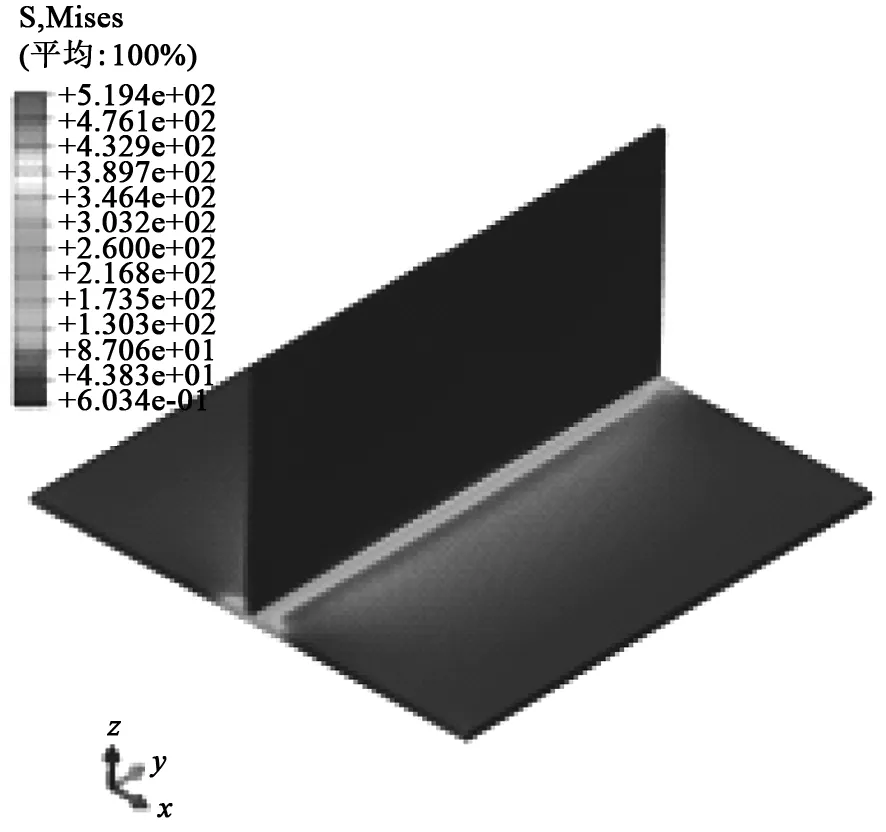
图9　T型接头等效应力云图

图10　T型接头最大主应力云图

图11　T型接头最小主应力云图

T型接头的应变分布结果如图12～图14所示。由图12～图14得知，焊后在焊缝周围的应变值较大，远离焊缝的区域应变值较小。取焊缝横截面，可计算得出焊缝横截面的平均固有应变。通过坐标轴方向得知，PE11为横向固有应变，PE22为纵向固有应变。

图12　T型接头X方向应变云图

图13　T型接头Y方向应变云图

图14　T型接头Z方向应变云图

2.3角接接头仿真结果

角接接头的应力分布如图15～图17所示。由图15～图17得知，焊后在焊缝周围的应力值较大，远离焊缝的区域应力值较小，焊接残余应力主要集中在焊缝及其附近。

图15　角接接头等效应力云图

图16　角接接头最大主应力云图

图17　角接接头最小主应力云图

角接接头的应变分布结果如图18～图20所示。由图18～图20得知，焊后在焊缝周围的应变值较大，远离焊缝的区域应变值较小。取焊缝横截面，可计算得出焊缝横截面的平均固有应变。通过坐标轴方向得知，PE11为横向固有应变，PE22为纵向固有应变。

图18　角接接头X方向固有应变云图

图19　角接接头Y方向固有应变云图

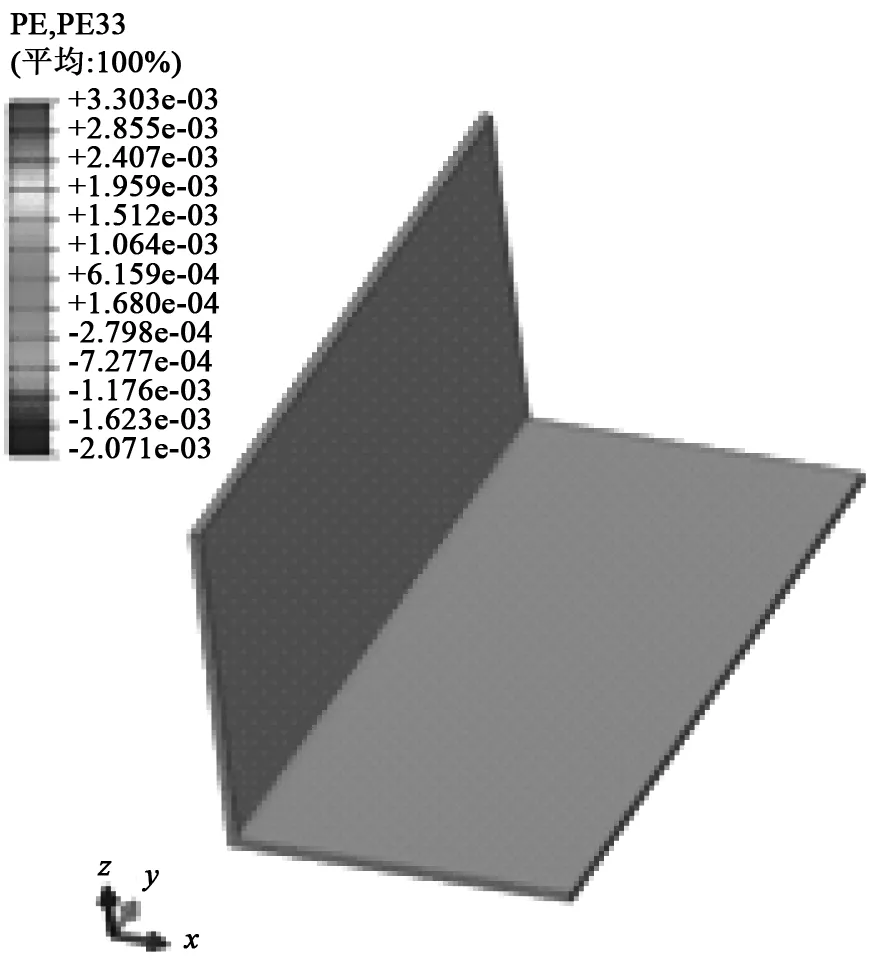
图20　角接接头Z方向固有应变云图

3　焊接工艺参数对应力及应变分布的影响

3.1焊接电流对桅杆焊缝仿真结果的影响

选取工艺参数为电压27 V、焊接速度25 m/h，电弧热效率0.75，依次选取焊接电流240、260、280、300和320 A，分别计算不同电流下，焊缝周围的应力和应变结果。

随着电流的不断增大，焊缝周围的残余等效应力变化趋势如图21所示。由图21得知，随着焊接电流不断增大，焊缝周围的等效应力数值不断增大，当电流增大到一定数值时，等效应力增大的趋势趋于平稳。

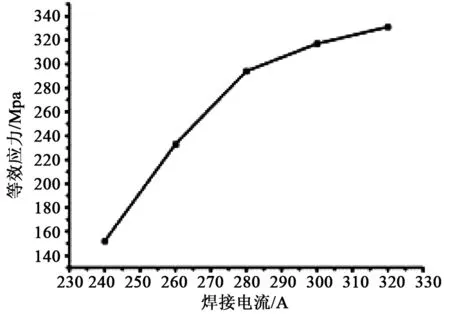
图21　焊缝等效应力随电流增大的变化趋势

随着电流的不断增大，焊缝周围的纵向固有应变变化趋势如图22所示。由图22得知，焊缝周围的纵向固有应变为负值，随着焊接电流不断增大，焊缝周围的纵向固有应变数值不断增大，当电流增大到一定数值时，纵向固有应变增大的趋势趋于平稳。

图22　焊缝纵向固有应变随电流增大的变化趋势

随着电流的不断增大，焊缝周围的横向固有应变变化趋势如图23所示。由图23得知，焊缝周围的横向固有应变为负值，随着焊接电流不断增大，焊缝周围的横向固有应变数值不断增大。

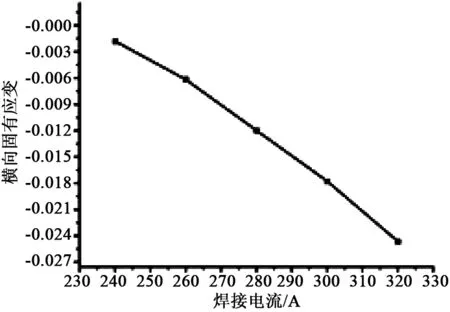
图23　焊缝横向固有应变随电流增大的变化趋势

3.2焊接电压对桅杆焊缝仿真结果的影响

选取工艺参数为电流260 A、焊接速度25 m/h，电弧热效率0.75，依次选取焊接电压24、27、30和33 V，分别计算不同电压下，焊缝周围的应力和应变结果。

随着电压的不断增大，焊缝周围的残余等效应力变化趋势如图24所示。由图24得知，随着焊接电压不断增大，焊缝周围的等效应力数值不断增大。

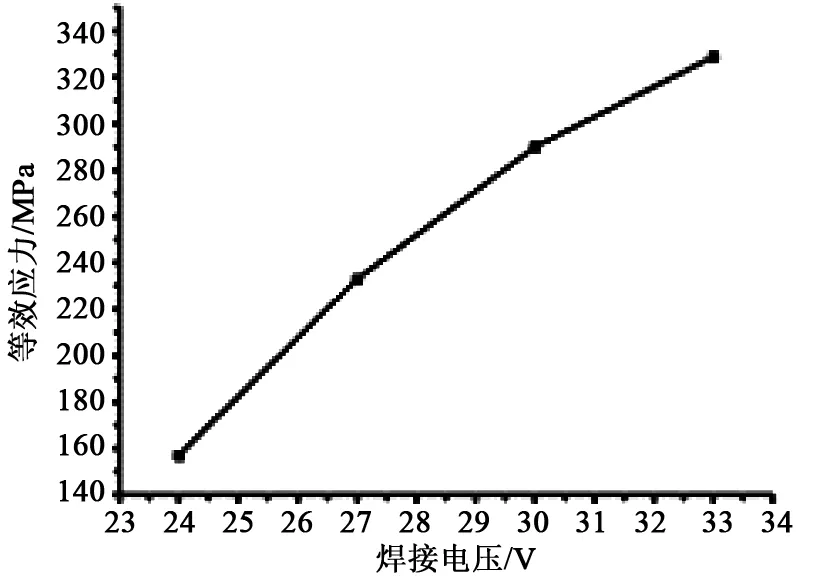
图24　焊缝等效应力随电压增大的变化趋势

随着电压的不断增大，焊缝周围的纵向固有应变变化趋势如图25所示。由图25得知，焊缝周围的纵向固有应变为负值，随着焊接电压不断增大，焊缝周围的纵向固有应变数值不断增大。

图25　焊缝纵向固有应变随电压增大的变化趋势

随着电压的不断增大，焊缝周围的横向固有应变变化趋势如图26所示。由图26得知，焊缝周围的横向固有应变为负值，随着焊接电压不断增大，焊缝周围的横向固有应变数值不断增大。

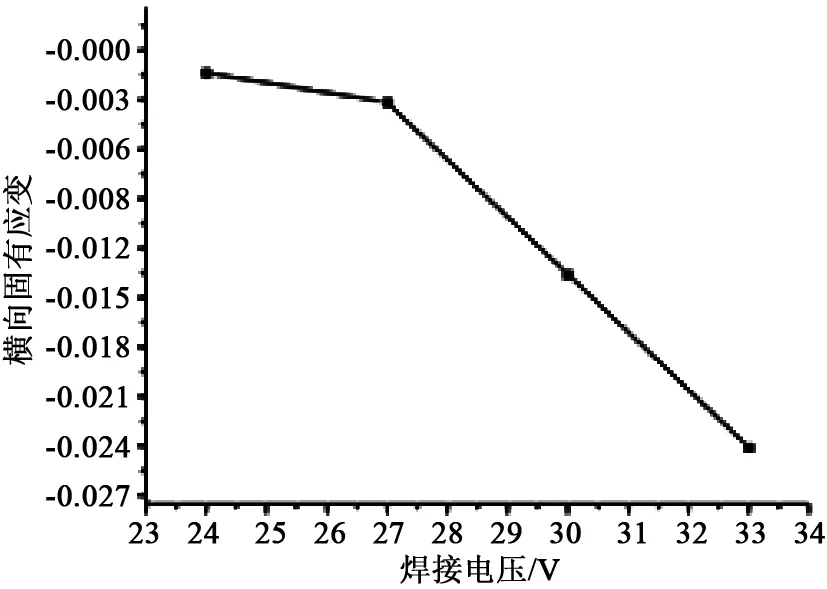
图26　焊缝横向固有应变随电压增大的变化趋势

3.3焊接速度对桅杆焊缝仿真结果的影响

选取工艺参数为电流260 A、焊接电压27 V，电弧热效率0.75，依次选取焊接速度20、25、30和35 m/h，分别计算不同焊接速度下，焊缝周围的应力和应变结果。

随着焊接速度的不断增大，焊缝周围的残余等效应力变化趋势如图27所示。由图27得知，随着焊接速度不断增大，焊缝周围的等效应力数值不断减小，当焊接速度增大到一定数值后，等效应力减小的趋势趋于平稳。

图27　焊缝等效应力随焊接速度增大的变化趋势

随着焊接速度的不断增大，焊缝周围的纵向固有应变变化趋势如图28所示。由图28得知，焊缝周围的纵向固有应变为负值，随着焊接速度不断增大，焊缝周围的纵向固有应变数值不断减小，当焊接速度增大到一定数值后，纵向固有应变减小的趋势趋于平稳。

图28　焊缝纵向固有应变随焊接速度增大的变化趋势

随着焊接速度的不断增大，焊缝周围的横向固有应变变化趋势如图29所示。由图29得知，焊缝周围的横向固有应变为负值，随着焊接速度不断增大，焊缝周围的横向固有应变数值不断减小，当焊接速度增大到一定数值后，横向固有应变减小的趋势趋于平稳。

图29　焊缝横向固有应变随焊接速度增大的变化趋势

4　桅杆焊接变形仿真

将上述得到的焊缝周围的固有应变值作为初始应变施加于桅杆模型中，采用固有应变法通过弹性仿真分析桅杆焊后的变形[10-11]。 通过固有应变法仿真得到的桅杆焊后整体变形如图30～图33所示。

图30　桅杆焊后整体变形云图

图31　桅杆变形放大图(300倍)

图32　桅杆Y向变形云图

图33　桅杆Z向变形云图

由图30～图33得知，桅杆在组装焊接后存在翘曲变形，中间的变形较大，两端的变形较小，整个模型沿轴线方向存在圆弧状的变形趋势，与实际焊接变形相吻合。

提取桅杆沿同一轴线方向的节点形成路径1(见图34)，得到沿路径1桅杆的变形趋势如图35～图37所示。由图35得知，桅杆焊后沿同一轴线呈现圆弧状的变形。由图36得知，桅杆焊后沿同一轴线在Y向的变形呈现圆弧状。由图37得知，桅杆焊后沿同一轴线在Z向的变形呈现圆弧状。

图34　路径1示意图

图35　沿路径1变形趋势

图36　沿路径Y向变形趋势

图37　沿路径Z向变形趋势

5　结语

本文基于固有应变法对桅杆的焊接成型工艺进行仿真，先通过三维弹塑性有限元仿真，得到焊接成型过程中典型焊接接头焊缝周围的残余应力分布和固有应变分布趋势，进而将获得的固有应变作为初始应变施加于桅杆模型中，通过固有应变法获得桅杆焊后的整体变形。

桅杆在组装焊接后整体存在翘曲变形，中间的变形较大，两端的变形较小，提取桅杆沿同一轴线方向的节点，整个模型沿轴线方向存在圆弧状的变形趋势，与实际焊接变形相吻合。

[1]汪建华，魏良武. 焊接变形和残余应力预测理论的发展和应用前景(1)[J]. 焊接，2001(9)：5-7.

[2]汪建华，魏良武. 焊接变形和残余应力预测理论的发展和应用前景(2)[J]. 焊接，2001(10)：4-6，34.

[3]汪建华，陆皓，魏良武. 固有应变有限元法预测焊接变形理论及其应用[J]. 焊接学报，2002，23(6)：36-40.

[4]周晶. 采用固有应变法预测铝合金焊接变形[J]. 焊接技术，2010(6)：6-10.

[5]陈楚. 数值分析在焊接中的应用[M]. 上海：上海交通大学出版社，1985.

[6]陈楚，汪建华，杨洪庆. 非线性焊接热传导的有限元计算和分析[J]. 焊接学报，1983(3)：139-148.

[7]汪建华，陈楚. 不同接头形式下的焊接传热计算机系统[J].焊接学报，1990,11(1)：57-64.

[8]Inoue T.Metallo-thermo-mechanics application to phase transformation incorporated processes[J].Theoretical Prediction in Joining and Welding, 1996(11):89-112.

[9]Masubuchi K. Prediction and control of residual stresses and distortion in welded structures[J].Transactions of Jwri, 1996,25:53-67.

[10]徐济进. 基于固有应变筒体对接多道焊焊接变形的预测[J]. 焊接学报，2007(1):77-80.

[11]奥凯尔渤洛姆 H O.焊接应力与变形[M]. 北京：中国工业出版社，1958.

责任编辑马彤

Based on the Inherent Strain of Mast Welding Process Simulation

HU Zhangwen1， XIONG Yiqun1， MU Jun1， WANG Haibo1， ZHENG Xuan2， HU Lingyun2，PANG Hongliang2， HUANG Yu2， ZHANG Long2

(1.Beijing Sany Heavy Machinery Co., Ltd.， Beijing 102206,China； 2.Beijing Semboo Science & Technology Co.,Ltd., Beijing 100086, China)

The mast of molding process is welding while the steel material is Q345B, the mast welding assembly is composed of base plate, side panel, roof and reinforcement of welding. Masts exist deformation after welding, it needs adopting the hot school to reduce the control deformation. The article is based on the inherent strain of mast welding molding process simulation. The welding forming is obtained by 3D elastic-plastic finite element silmulation in the process of inherent strain distribution around the weld residual stress distribution and trend. The whole welding deformation is through using inherent strain gauge and mast.

welding， mast， the inherent strain gauge， three dimensional elastoplastic finite element method， weld stress and strain distribution

TG 404

A

胡掌稳(1970-)，男，高级工程师，主要从事焊接等方面的研究。

2016-02-22