微分几何在平面曲线测设中的应用

师军良,孙清娟

(黄河水利职业技术学院，河南 开封 475004)



微分几何在平面曲线测设中的应用

师军良,孙清娟

(黄河水利职业技术学院，河南 开封 475004)

提出了利用微分几何原理计算曲线测设参数，建立了适用于所有平面曲线类型(直线、单圆曲线、缓和曲线)的测设参数计算模型，具有计算简便、实用性强等特点，且易于在计算机上编程实现。通过在高速公路的实际应用，表明该方法可适用于各种平面线形测设数据计算，能够满足工程施工的要求。

微分几何；平面曲线；测设；曲率变化率

在公路、铁路等线型工程勘测设计过程中，由于受地形、地质等因素影响，经常无法按运营效率最高的直线设计线路，需要将线路转变方向，即在两条直线线路之间插入平面曲线。平面曲线有单圆曲线、综合曲线(缓和曲线和单圆曲线)、回头曲线等形式[1]。

平面曲线测设是线路勘测设计阶段的一项主要测量工作，现有的测设方法均是根据平面曲线的具体线型及曲线的平面几何特性，选择相应独立的计算模型和测设方法，如切线支距法、偏角法等[2]。目前最为常用的方法是通过选择的曲线模型计算出主点坐标，然后用全站仪或GPSRTK直接进行坐标法测设出主点实际位置。由于线路由直线转入曲线段后，既有缓和曲线段，又有中间的圆曲线段，这些线段都需要根据各自的数学模型进行分段计算，使得计算量大且较为繁琐，不利于在计算机上用自编程序进行自动解算。针对上述存在的问题，本文基于微分几何原理研究建立适应于所有平面曲线类型测设的算法模型，实现各种平面曲线统一、高效、简便的测设计算，且易于在计算机上编程实现，通过在日南(日照—南阳)高速公路某标段线型勘测设计中的实际应用，表明该算法模型能够满足施工精度要求。

一、基于微分几何原理的平面曲线测设计算模型

1. 基于微分几何原理的平面曲线测设计算方法

公路线路的线形主要为直线、单圆曲线、缓和曲线，直线可以视为半径为无穷大的曲线，单圆曲线可以看成是半径为r的曲线，缓和曲线则是半径在(r，∞)范围渐变的曲线。如果已知曲线上一系列点的平面坐标，根据工程测量学知识可将该曲线测设出来[3]。如图1所示，设过某曲线起始点A的切线的方位角为αA，该曲线上任意点i的切线与过曲线起点A的切线的夹角为β，点i的切线方位角αi；若A点坐标(xA，yA)已知，依据平面几何关系可知

αi=αA+β

(1)

则计算曲线上任一点坐标的积分公式为[4]

(2)

由式(2)可以看出，计算曲线任意点i的坐标时，如果已知曲线上任意点i的3个特征参数，即曲线起点A的平面坐标、切线坐标方位角αA和过任意点i的切线与过曲线起点A的切线的夹角β，就可以求出弧长li的i点平面坐标(xi，yi)[5]。

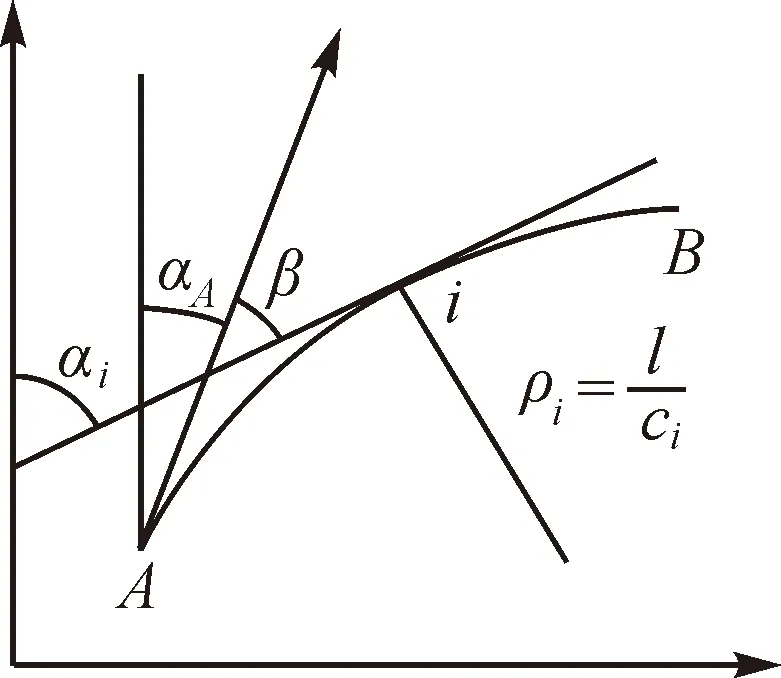
图1　曲线上点的坐标

2. 曲线上任意点的坐标计算方法

(1) 曲线上任意点的切线坐标方位角

(3)

(2) 曲率变化率

若曲线上微分段dl对应的曲率变化量为dρ，则由定义可知，曲率变更率c为

(4)

ρi=ρA+cl

(5)

将式(5)代入式(3)，积分后得到

(6)

于是式(1)可表达为

(7)

(3) 曲线上任意点的坐标计算

只要计算出曲线上任意点i的切线方位角αi，即可推算出该点的平面坐标，即将式(7)代入式(2)，则点i的平面坐标为

(8)

将式(8)用三角函数展开，得

(9)

(10)

用泰勒级数将式(9)展开，并将弧长保留到5次项，再对其进行积分后整理为[8]

(11)

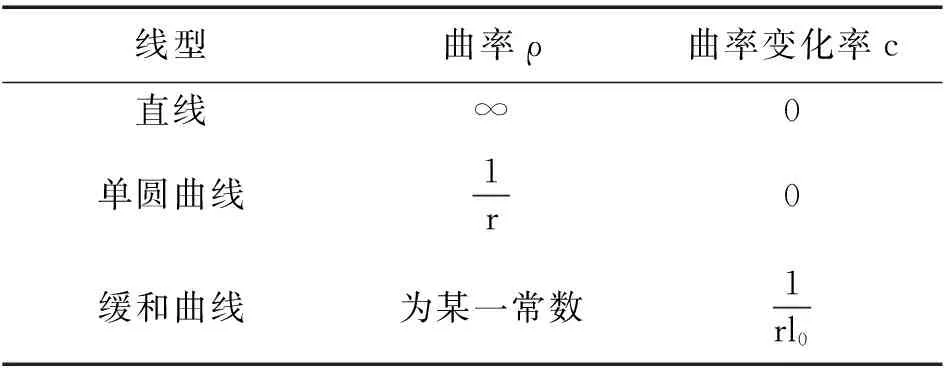
表1　各种线形曲线的曲率变化率

二、实际应用

图2　日南高速某标段形式

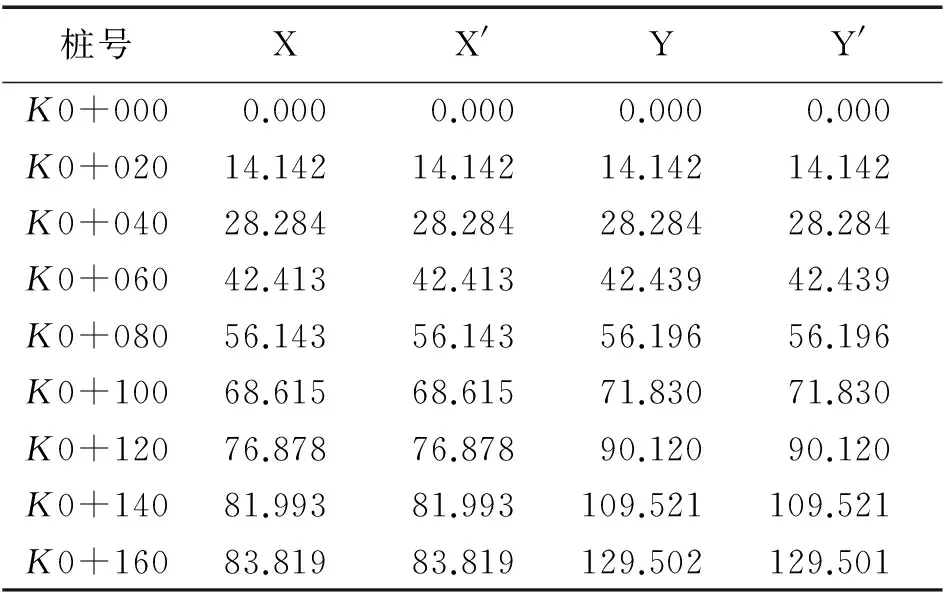
表2中，(X，Y)是由式(11)计算得到的测设坐标，(X′，Y′)则是根据曲线独立模型计算出来的测设坐标。

通过对测设数据的比较分析可以得出：在160m的弧长中，点位误差仅为1mm，完全能够满足工程施工的要求。由于式(11)可以对任何平面曲线进行任意点的平面坐标计算(统一了平面曲线数学计算模型)，从而避免了多个独立数学计算模型的繁琐工序。

三、结束语

本文提出利用微分几何原理计算曲线测设参数，建立了适用于所有平面曲线类型(直线、单圆曲线、缓和曲线)的测设计算模型，通过日南高速公路某标段的实际应用，表明该方法能够满足高速公路施工精度要求。此外，本方法更适合计算机程序化处理，可有效降低线路中线坐标的计算时间，显著提高线路测设的工作效率。

[1]李青岳，陈永奇.工程测量学[M].北京：测绘出版社，2000.

[2]许永，李孟山，李少元.线路测量一体化数学模型[J].测绘通报, 1996(1):39-41.

[3]冯晓，李方，邓学钧.组合空间曲线任意点三维大地坐标的算法研究[J].测绘学报，1996，25(2):141-144.

[4]刘仁钊,伍吉仓.平面曲线测设的理论及应用[J]. 资源环境与工程，2009(4): 164-167.

[5]李少元,王新洲,花向红.道路平面测设计算的通用公式[J].测绘工程, 2006(4):17-21.

[6]杨存吉,李全信.线路中线测设的统一数学模型[J].测绘通报, 2001(2):14-15.

[7]张学山，王天波.浅谈平面曲线的曲率[J].上海工程技术大学教育研究, 2006(2):37-40.

[8]同济大学数学系.高等数学[M].北京：高等教育出版社，2007.

[9]周建郑.工程测量[M].郑州：黄河水利出版社, 2006.

[10]孙孝军.公路、铁路施工测量的实用计算器程序[J].测绘通报, 2006(7):26-29.

The Application of Infinitesimal Geometry in Plane Curve Location

SHI Junliang,SUN Qingjuan

2016-03-20

矿山空间信息技术国家测绘地理信息局重点实验室开放基金；河南理工大学2013年度博士基金(B2013-018)

师军良(1979—)，男，硕士，讲师，主要从事测绘科学与技术的研究与教学工作。E-mail:454888231@qq.com

P258

B

0494-0911(2016)08-0092-03

引文格式：师军良,孙清娟.微分几何在平面曲线测设中的应用[J].测绘通报，2016(8)：92-94.DOI:10.13474/j.cnki.11-2246.2016.0265.