基于PBIL算法的无线传感器网络三维定位方法
刘 宏,王其涛,夏未君
(江西理工大学 电气工程与自动化学院,江西 赣州 341000)
基于PBIL算法的无线传感器网络三维定位方法
刘宏,王其涛,夏未君
(江西理工大学 电气工程与自动化学院,江西 赣州341000)
为了提高无线传感器网络节点的三维定位精度,提出了基于人口增量学习(population based incremental learning,PBIL)算法的无线传感器网络三维定位方法;算法首先通过RSSI技术进行测距,设立阈值消除包含误差较大的测量距离,然后使用人口增量学习算法对适应度函数进行求解,根据Heb规则更新概率向量并产生新的个体,最后经过循环寻优得到最优解;利用MATLAB进行仿真,结果表明:算法的定位精度和稳定性相较于最大似然法有了明显的提高。
无线传感器网络;测距;PBIL;三维定位
0 引言
随着无线通信、数据融合等技术的发展,无线传感器网络[1](wireless sensor networks,WSN)的发展也取得了长足的进步,使其在智慧地球中发挥着越来越大的作用。在实际应用中,无线传感器网络工作的环境往往是高突不平的,同时人们对信息质量的要求也越来越高,二维平面定位技术已经越来越无法满足需求,因此实现WSN节点快速而准确的三维定位就显得尤为重要[2]。
把进化算法[3](evolutionary algorithms, EAs)应用于WSN节点定位是众多专家学者的研究重点,文献[4]使用遗传算法对DV-hop算法得到的位置坐标进行校正,算法在不提高成本的情 况下,相较于DV-hop算法提高了定位精度并扩大了定位范围;文献[5]对蝙蝠算法加以改进并应用于无线传感器网络节点定位中,降低了平均跳距引起的定位误差,提高了网络节点的定位精度;文献[6]把蚁群算法应用于矿井下的WSN节点定位中,在不添加多余硬件条件下提高了定位精度;文献[7]在无线传感器网络节点定位中引入量子遗传算法,利用量子遗传算法求解模型获得的最优解作为节点的定位坐标,提高了网络的稳定性和定位精度。传统上采用最大似然法(ML算法)求解非线性方程组得到未知节点的坐标,但较大的测距误差导致定位精度很差,因此本文在无线传感器网络节点三维定位中引入基于人口增量学习[8](population based incremental learning,PBIL)算法。仿真结果表明:方法不但提高了节点的三维定位精度,同时也可以在较低的连通度下实现较高的定位精度,网络的稳定性也较高。
1 RSSI测距及最大似然法
无线传感器网络中的测距技术共有4种:以电磁波到达时间为基础的TOA、以电磁波和声波到达时间差为基础的TDOA、以发射信号角度为基础的AOA和以射频信号强度为基础的RSSI。RSSI测距技术是在路径损耗和发射端信号强度已知的情况下,通过测量接收信号强度计算两点间的距离。由于现有的商用芯片都可以测量射频信号的强度,无需添加额外的硬件。因此使用RSSI测距技术的无线传感器网络技术成熟、价格便宜、使用方便、广受欢迎。
由于多径、绕射等不确定因素的存在,它们单个有时甚至叠加起来,产生严重的干扰,影响了未知节点接收信号的强度,从而导致测量距离中含有不同比例的测距误差。因此选择对现实因素考虑最多的路径损耗模型:对数-常态分布模型[9],设PL(d0)[dB]为发射端信号强度,PL(d)[dB]为接收端信号强度:
PL(d)[dB]=PL(d0)[dB]+10nplg(d/d0)+Xσ
(1)
式中,d为M(锚节点)与N(未知节点)之间的测量距离;d0为取值1 m的近地参考距离;np为路径损耗指数;Xσ为高斯随机误差。
由于Xσ是正态0均值,在实际应用中可以简化计算模型,得出测量距离d为:
(2)
由于测量距离d存在测距误差,传统上使用最大似然法完成无线传感器网络的节点定位。设未知节点为N(x,y,z),锚节点为M1(x1,y1,z1)、M2(x2,y2,z2)、M3(x3,y3,z3)、…、Mk(xk,yk,zk),则存在如下关系式:
(3)
对式(3)进行求解得到未知节点的坐标X:
(4)
式中,
由于d存在测距误差,导致式(3)是非线性的,当测距误差较大时,未知节点的定位精度变的较差,因此可以使用进化算法依据适应度函数寻找最优坐标。
2 PBIL算法基本原理
PBIL算法是一种新型的进化算法,算法的个体使用概率模型进行描述,通过统计学习手段从宏观上对群体进行描述,然后依据概率模型产生新的个体,反复进行并最终实现群体的进化。PBIL算法自提出以来就受到广泛的关注,其控制参数少、简单易实现,在解决多维度问题上比遗传算法更有效,同时也降低了时间的复杂性,是一个较理想的优化算法。
PBIL算法原理如下:
设s为解的个体,是一个二进制串且长度为w,si(i=1,2,3,…,n)为二进制串的第i个基因位,每个基因位的取值为0或者1,则优化问题表示如下:
minf(s)
(5)
式中,f为寻优适应度函数,最小适应值对应的个体为最优解。
同时设P=(p1,p2,p3,…,pn)为n维的概率向量,其中的pi表示当前个体中对应基因位si取值1的学习概率,则1-pi为取值0的学习概率,进化学习过程如下。
2)初始化学习概率P:概率向量pi=0.5,即进化初期si取0或1的概率是相等的。
2)生成解空间:由学习概率随机产生L个个体,则解空间为S=(s1,s2,s3,…,sl)。
3)计算适应值:依据适应度函数计算解空间所有个体的适应值并按照大小排序。
4)寻找最优个体组:按照排序好的个体,取出适应值最小的t(t≤L)个个体s1,s2,s3,…,st并组成最优解组sx。
5)修正概率向量:利用步骤四中的最优解组sx,采用机器学习中的Heb规则更新概率向量:
(6)
式中,r为学习速率:大小在[0.01,0.1]之间。r越小,收敛速度越慢,相对搜寻到的个体质量更优,相反,收敛速度更快,相对搜寻到的个体质量较差。
6)停止进化判断:若达到最大进化次数或者需要的精度,则算法停止,若未达到,则跳转至2)。
3 基于PBIL算法的定位方法表述
3.1跳出局部最优方法
PBIL算法和其它进化算法一样,在求解非线性多维问题时可能存在局部最优[10],这是因为在进化过程中对概率模型进行学习时,解空间拟合度会慢慢增大,在算法进化后期,种群多样性会迅速减小,从而陷入局部最优,因此本算法在寻优后期引入遗传算法中的交叉变异操作,维持种群多样性在一定的水平,从而抑制局部最优解的产生,使寻优工作继续进行下去。
3.2适应度函数
WSN定位误差源于RSSI的测距误差,因此本文通过剔除误差较大的测量距离和在适应度函数中添加权值来抑制测距误差对定位精度的影响。
由于RSSI测距信号在近距离时衰减的很快,在远距离时信号衰减的较为缓慢,因此测量距离越近时测距误差越小,相反测距误差越大。设测距半径为R,根据RSSI测距误差变化规律:测量距离小于0.5R时,测距误差平均小于0.1R;测量距离在0.5R和0.75R之间时,测距误差平均在0.1R和0.2R之间;测量距离大于0.75R时,测距误差平均在0.2R和0.4R之间,个别测距误差甚至达到0.5R。因此必须设立阈值消除测距误差较大的测量值,阈值设立如下:
W=0.75R
(7)
式中,W为阈值,即当未知节点通信范围内接收到的测距信号多于4时,即可启用阈值设定并消除误差较大的d(d≥W)。
适应度函数值表示当前解的优劣,较小的适应值对应解得质量较高,相反解得质量较小。设当前经PBIL算法进化得到的最佳坐标为N(x,y,z),当前未知节点可连接的锚节点共有k个,第j个锚节点的坐标为M(xj,yj,zj),未知节点到第j个锚节点的距离为dj则可得:
(8)
由于测量距离越大,测距误差也越大,因此需要设立权值控制不同测量距离对定位精度的影响,较大的测量距离赋予较小的权值,反之赋予较大的权值,因此选择dj的倒数作为权值,适应度函数设计如下:
(9)
3.3PBIL定位算法流程
设群体最大进化次数为G,则基于PBIL算法的WSN三维定位流程图如图1所示。

图1 定位算法流程图
4 仿真实验
4.1实验设计
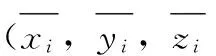
(10)
式中,m为未知节点总数。
4.2实验结果分析
1)不同连通度对局部最优解的影响:
进化算法在多维度问题上一般存在局部最优问题,在算法后期引入交叉变异操作可以较好的解决局部最优。本算法在测距误差为0时且未引入交叉变异的情况下,分析了连通度对局部最优解的影响,仿真结果如图2所示:由(a)可以得出在连通度为4时局部最优率为5%;由(b)可以得出在连通度为5时局部最优率为3%;由(c)可以得出在连通度为6时局部最优率为1%。随着连通度的增加不但局部最优率逐渐减小而且局部最优的节点的定位误差也在减小,在仿真过程中还发现当连通度大于10时,局部最优率小于千分之一。说明在无线传感器网络三维定位中除了可以在算法中引入交叉变异来消除局部最优解,还可以增加连通度来抑制局部最优解。

图2 不同连通度下的局部最优情况
2)稳定性及定位精度对比:
在连通度为5、测距误差为20%的情况下共测试120个节点的定位误差,形成的误差曲线如图3所示,进一步对数据进行处理,结果如表1所示。在表1中可以得出PBIL算法的最大、最小定位误差差值为0.075 3,ML算法的最大、最小定位误差差值为0.189 1,说明PBIL算法比ML算法的定位精度的波动性更小;PBIL算法的平均定位误差比ML算法小了0.099 6,说明PBIL算法的定位精度更高;PBIL算法的标准差比ML算法小了0.029 6,说明PBIL算法的稳定性更高。从图3中的定位误差曲线也可以直观的得出PBIL算法无论在定位精度还是稳定性比ML算法都要高。

表1 稳定性分析
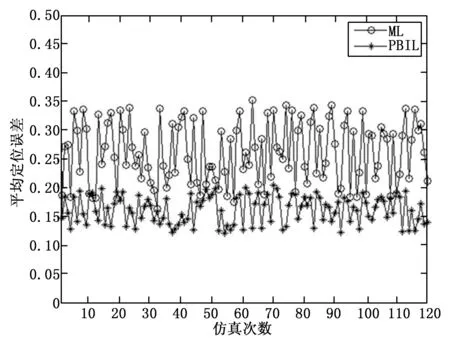
图3 PBIL与ML定位误差曲线对比
3)测距误差和定位精度的关系:
在实际环境中RSSI测距信号在近距离时衰减很快,在远距离时衰减的较为缓慢,导致在距离较远时的测距误差急剧增大,因此在较大测距误差下维持一个较高的定位精度就现的尤为重要。因此在连通度为5时测试不同测距误差下的平均定位误差,结果如图4所示。由图4可以看出随着测距误差的增大ML算法的误差曲线斜率几乎不变,定位误差增加的很快,而PBIL算法的误差曲线的斜率一直在下降,定位误差的增长较为缓慢。还可以看出2种算法的平均定位误差差值也随着测距误差的加大而增大。说明PBIL算法比ML算法的抗干扰能力更强,在测距误差较大的情况下也维持较好的定位精度。

图4 对比不同测距误差下的平均定位误差
4)平均连通度和定位精度的关系:
在较低的连通度下实现较高的定位精度以及减小连通度对定位精度的影响是无线传感器网络三维定位技术追求的目标之一。在测距误差为20%时,测试连通度由4到13平均定位误差的变化情况,结果如图5所示。可以得出:PBIL算法和ML算法在连通度为4到7时平均定位误差下降速度较快,在连通度为8到13是下降的较为缓慢;PBIL算法连通度由4到13时,平均定位误差共下降0.038 1,ML算法共下降了0.080 1,说明PBIL算法受连

图5 对比不同连通度下的平均定位误差
通度的影响更小,在较小的连通度下就可以得到较高的定位精度,较适合应用在锚节点稀疏的网络。
5 结束语
为了减小测距误差对无线传感器网络三维定位精度的影响,提出了一种基于人口增量学习(PBIL)算法的定位方法。算法在RSSI测距的基础上,使用PBIL算法对适应度函数进行求解,同时通过仿真研究了本算法的性能,分析了不同连通度下对局部最优的影响,测试了稳定性,对比了测距误差、连通度对定位精度的影响。仿真结果表明:PBIL算法在较高的连通度下能很好的抑制局部最优解,同时在定位精度和稳定性方面比ML算法有了较大的提高。
[1]赵仕俊,唐懿芳.无线传感器网络[M].北京:科学出版社,2013.
[2]Mert B,Liu M,Shen W M,et al.Localization in cooperative wireless sensor networks: A review[A].Proceedings of the 2009 13th International Conference on Computer Supported Cooperative Work in Design[C]. 2009:438-443.
[3]Thomas J.Analyzing evolution algorithms[M].Berlin Heidelberg:Springer-verlag,2013.
[4]邓力.基于遗传算法WSN节点定位算法研究[J].计算机仿真,2011,28(9):161-164.
[5]赖锦辉.基于蝙蝠优化算法的无线传感器网络节点定位研究[J].计算机测量与控制,2014,22(8):2709-2712.
[6]梁美玉,李莉,陈坤.基于蚁群算法的井下无线传感器网络节点定位研究[J].煤矿机械,2010,31(12):48-50.
[7]方旺盛,曾晶.基于量子遗传算法的非测距节点定位算法研究[J].计算机应用与软件,2013,30(2):180-183.
[8] Yang Shengxiang,Yao Xin.Experimental study on population-based incremental learning algorithms for dynamic optimization problems[J].Soft comput,2005,(9):815-834.
[9]方震,赵湛.基于RSSI测距分析[J].传感技术学报,2007,20(11):2526-2530.
[10]Hohfeld M,Rudolph G.Towards a theory of population based incremental learning[A].In: Proceedings of the 4th International Conference on Evolutionary Computation[C]. IEEE, 1997: 1-5.
A Method of the WSN Three-dimensional Positioning Based on PBIL Algorithm
Liu Hong,Wang Qitao,Xia Weijun
(School of Electrical Engineering and Automation,Jiangxi University of Science and Technology, Ganzhou341000,China)
In order to improve the three-dimensional positioning accuracy of wireless sensor network node, it is proposed that wireless sensor network three-dimensional positioning method based on the population based incremental learning algorithm.At first,the algorithm by RSSI measurement of the distance and set a threshold to eliminate the error containing big measuring distance.Then it uses the population based incremental learning algorithm to find the solution to the fitness function, and according to the rules of Heb,it updates probability vector and produces new individual.Finally,it obtains the optimal solution by the cycle optimization. Through using Matlab simulation, its results show that the positioning accuracy and stability of the algorithm had obvious improvement compared with maximum likelihood method.
wireless sensor network; ranging; PBIL; three-dimensional positioning
2015-07-13;
2015-08-25。
国家自然科学基金资助项目(61163063)。
刘宏(1968-),男,江西萍乡人,副教授,硕士研究生导师,主要从事无线传感器网络基础设施的理论和技术方向的研究。
1671-4598(2016)01-0334-04
10.16526/j.cnki.11-4762/tp.2016.01.093
TP393
A

