基于BP神经网络的排爆机械臂逆运动学分析
李文博,曹 兵,张云波
(南京理工大学 机械工程学院, 南京 210094)
基于BP神经网络的排爆机械臂逆运动学分析
李文博,曹兵,张云波
(南京理工大学 机械工程学院, 南京210094)
机械臂逆运动学是已知末端执行器的位姿求解机械臂各关节变量,主要用于机械臂末端执行器的精确定位和轨迹规划,如何高效的求解机械臂运动学逆解是机械臂轨迹控制的难点;针对传统的机械臂逆运动学求解方法复杂且存在多解等问题,提出一种基于BP神经网络的机械臂逆运动学求解方法;以四自由度机械臂为研究对象,对其运动学原理进行分析,建立BP神经网络模型并对神经网络算法进行改进,最后使用MATLAB进行仿真验证;仿真结果表明:使用BP神经网络模型求解机械臂逆运动学问题设计过程简单,求解精度较高,一定程度上避免了传统方法的不足,是一种可行的机械臂逆运动学求解方法。
机械臂;逆运动学;神经网络;最优化算法
0 引言
排爆机器人用于代替排爆人员搬运、转移和销毁可疑爆炸物及其它有害危险品,有效避免了不必要的人员伤亡。目前,排爆机器人在发达国家应用广泛,而我国由于起步较晚,仍处于快速发展阶段。排爆机器人的机械臂运动学包括正运动学和逆运动学两部分[1]。其中机械臂逆运动求解问题是机械臂运动学分析的难点,一直受到国内外机器人研究者的关注。
机械臂逆运动学求解是正运动学求解的反过程,属于非线性问题。机器人逆运动学求解的传统方法有迭代法、解析法和几何法[2]。Paul等提出的机械臂运动学解析解法对后来的机械臂逆运动学问题研究具有指导性的作用[3]。Regnier等提出一种基于迭代法和分布式的算法,能够求出多种结构的六自由度机械臂的位置逆解[4]。徐德等系统地分析了5自由度机械臂的正运动学和逆运动学,证明该机械臂不存在奇异性位姿问题[5]。蒋宏超等采用矩阵逆乘的解析解法求解机械臂的正运动学模型,得到六自由度机械臂逆运动学的完整解析解[6]。李宪华等针对六自由度模块化串联机械臂,提出采用几何方法求解机械臂前3个关节、使用反变换法求解后3个关节的组合解法,得到了机械臂逆运动学的完整解析解[7]。以上方法都可以求解机械臂逆运动学问题,但具有一定的局限性,而且求解过程复杂,涉及多解和奇异性等问题。随着科技的发展,机器人的设计要求越来越高,这些传统方法已经满足不了机器人的性能需求。因此,有必要寻求一种新的方法来求解机械臂逆运动学。近年来,人工神经网络作为一种新技术引起了研究者的兴趣,神经网络是一种模仿人类神经网络行为特征,进行分布式并行信息处理的算法数学模型[8]。
机械臂逆运动学求解是一个复杂的非线性问题,而BP神经网络具有较好的非线性拟合能力,LM(Levenberg-Marquardt)最优化训练方法收敛速度快,特别适用于数据量较大的复杂模型。因此,文中结合BP神经网络和LM优化算法设计一个三层BP神经网络模型来求解机械臂逆运动学,重点分析四自由度机械臂的逆运动学求解,通过仿真不断调整神经网络的模型参数,选取出仿真结果较好的参数,并对仿真结果进行分析。
1 排爆机械臂运动学分析
文中以实验室自主研发的排爆机械臂为分析对象,该机械臂由5个步进电机驱动,包含4个转动关节和一个末端夹手,末端夹手只控制夹取物体,与运动学无关,所以运动学分析时忽略夹手关节,其余的4个关节分别为底座回转、大臂回转、小臂回转、手爪回转。
1.1建立机械臂坐标系
(1)

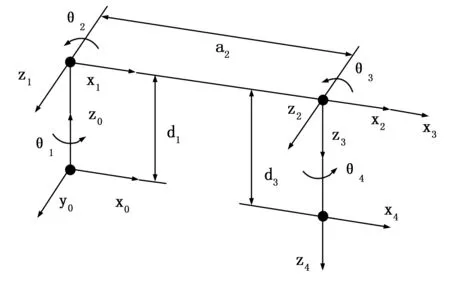
图1 机械臂坐标系
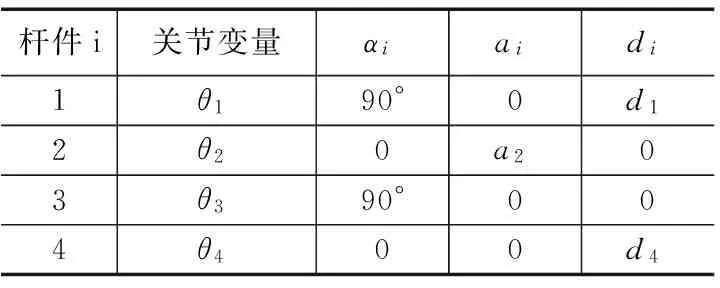
杆件i关节变量αiaidi1θ190°0d12θ20a203θ390°004θ400d4
1.2正运动学分析

(2)
nx=c1c2c3c4+s1s3c4;ny=-c1s3c4
nz=s1c2c3c4;ox=-c1c2c3s4-s1s3s4+s1c4
oy=c1s3s4-c1c4;oz=-s1c2c3s4
ax=c1c2s3+c1s2c3;ay=0
az=s1c2s3+s1s2c3-c2c3
px=d4c1s23+a2c1c2;py=0
pz=d4(s1s23-c2c3)+a2(s1c2+s2)+d1
其中:si=sinθi;ci=cosθi;sij=sin(θi+θj)
1.3逆运动学分析

(3)
(4)
令式(3)式(4)的对应项(2,1)相等可以求得关于θ1的两组解:
(5)
(6)
令式(3)式(4)的对应项(1,3)(1,4)分别对应相等可以求得θ2的解:
(7)
⟹{mathop{ m c} olimits}2=
(8)
令式(3)式(4)的对应项(2,3)相等可以求得θ3的解:
(9)
(10)
令式(3)式(4)的对应项(3,1)相等可以求得θ4的解:
(11)
(12)
以上是基于矩阵逆乘的解析法求解机械臂逆运动学,求得该四自由度机械臂存在两组解析解。但这种方法求解逆运动学时存在两点不足:1)机械臂各关节角度间存在复杂的耦合关系,使得解耦过程非常复杂;2)机械臂各关节角度与机械臂末端的空间位置是多对一的关系,传统的解析解很难得到单一的优化解,此时需要根据机械臂的结构特点选取优化解。而使用神经网络求解机械臂逆运动学可以避免解析法的不足,提高运算速度,满足系统实时性的需求。
2 BP神经网络设计
机械臂逆运动学求解实质就是由决定机械臂末端执行器位姿的12个变量去求解机械臂4个关节变量,这一过程可以使用神经网络模型来完成。神经网络具有非线性特征,能够很好的逼近任意复杂的非线性系统,能够处理多输入多输出系统,非常适合于多变量系统。
2.1神经网络结构设计
典型的BP神经网络包括输入层、隐含层和输出层,层与层之间采用全互联方式,同层之间不存在连接,隐含层可以有一层或多层,典型的三层网络拓扑结构如图2所示。
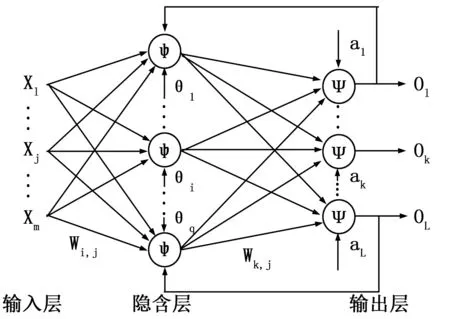
图2 典型三层BP神经网络结构图

(13)
神经网络的输出是机械臂的4个关节变量,构成输出向量o,如式(14)所示。
(14)
网络的学习速率决定每一次循环训练中所产生的权值变化量,一般情况下,倾向于选取较小的学习速率以保证系统的稳定性,学习速率的选取范围在0.01~0.8之间。隐含层的传递函数为tansig函数,由于整个网络的输出为任意值,所以输出层的传递函数为purelin函数。
2.2改进神经网络算法
基本BP神经网络的算法包括信号的前向传播和误差的反向传播,即计算实际输出按从输入到输出的方向进行,而权值和阀值的修正从输出到输入的方向进行[10]。误差的反向传播首先由输出层开始逐层计算各层神经元的输出误差,然后根据误差梯度下降法来调节各层的权值和阀值,使修正后网络的最终输出能接近期望值。系统对P个训练样本的总误差准则函数为:
(15)
BP算法的实质是求解误差函数的最小值问题。它采用非线性规划中的最速下降方法,按误差函数的负梯度方向修改权值,但这种算法在函数训练中存在学习效率低,收敛速度慢,易陷入局部极小状态等问题,所以需要对BP算法进行改进。
BP算法的改进主要有两种途径,一种是采用启发式学习算法,另一种是采用基于数值最优化理论的训练算法。文中使用LM最优化方法对神经网络进行训练。BP算法中牛顿法的收敛速度快,但在每一次的迭代中,牛顿法都需要求出表现函数的二次导数Hessian阵Ak,如式(16)所示,这就使得计算量变得很大,而LM方法不需要计算Hessian阵,Hessian阵可以用式(17)来近似替代:
(17)
其梯度为:
(18)
其中,J是雅克比(Jacobian)矩阵,它含有网络训练误差的一阶导数,是权值和阀值的函数。e是网络训练误差向量。则权值和阀值的调整公式如式(19)所示:
(19)
当μ=0时,式(18)变成具有近似Hessian阵的牛顿法。当μ较大时,LM算法就更接近小步长的梯度法。在迭代过程中,如果训练成功,就减小μ的值,如果训练失败,就增加μ的值,这样表现函数最终会减小到一定值[11]。
3 仿真与结果分析
MATLAB是一种用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,内部含有丰富的调用函数。文中使用MATLAB的robotics工具箱和神经网络工具箱对机械臂进行建模和仿真。
3.1仿真设计
利用MATLAB的Robotics工具箱建立四自由度机械臂的模型,依据机械臂的结构确定各关节变量的取值范围,如表2所示。

表2 各关节变量的取值范围
将各关节变量的取值范围均分为500份,在Robotics工具箱中进行正运动学求解,如此即可得到500组仿真数据。从500组数据中随机选取部分数据,将其代入到第二节所求的机械臂运动学方程中,求得的结果与模型一致,如此可以验证MATLAB所建模型是正确的。最后在500组数据中每隔9组选出1组作为神经网络的测试数据,共选出50组测试数据,其余的450组作为神经网络的训练数据。由于样本数据之间的差异比较大,不利于神经网络的训练,所以在训练前对样本进行归一化处理。
实验数据选定后,使用MATLAB神经网络工具箱对BP神经网络进行训练,神经网络训练流程图如图3所示。实验过程中不断的调整网络参数,经过一系列的仿真实验,对比实验结果,最后选定神经网络的基本参数如表3所示。
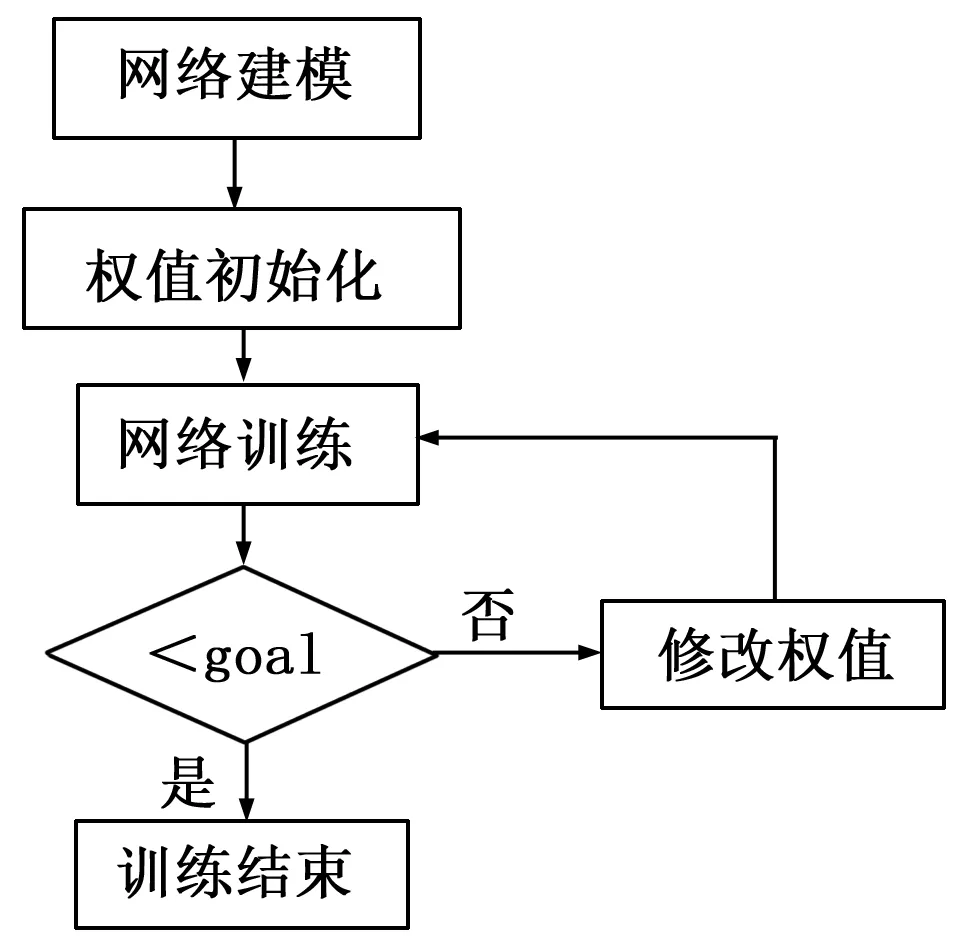
图3 神经网络训练流程图

网络参数设定值net.trainParam.epochs1000net.trainParam.goal0.001net.trainParam.lr0.05
3.2结果分析
文中分别采用不同的方法对神经网络进行训练,训练结果如表4所示,由于测试数据有50组,为便于对比分析,所以将变量的50组绝对误差表示为取值区间。对比训练结果可知,常规梯度下降法收敛速度较慢,误差较大;有动量的梯度下降法学习过程容易发生动荡,导致训练失败,而且其收敛速度慢,误差较大;有自适应lr的梯度下降法的收敛速度较快,误差较小;相比前3种方法,采用LM方法收敛速度最快,仅用了6次就达到训练的目标精度,绝对误差较小,仿真结果较好。
目前选取隐含层的神经元数在理论上还没有一个明确的规定,一般根据经验采取尝试法,通过对不同神经元数进行训练对比,依据对比结果进行选取。当采用LM最优化方法训练神经网络,使用不同组合的隐含层与输出层的神经元数得出的仿真结果如表5所示,仿真结果表明虽然不同的隐含层与输出层神经元数组合对仿真结果有影响,但其影响较小,小于使用不同训练算法对神经网络的影响。
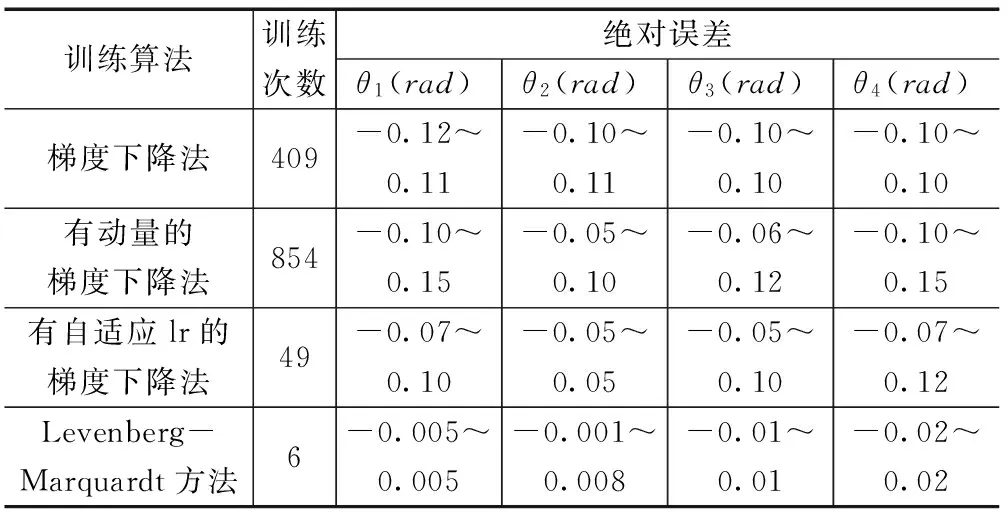
表4 使用不同算法的仿真结果

表5 不同神经元数组合的仿真结果
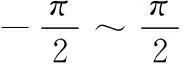
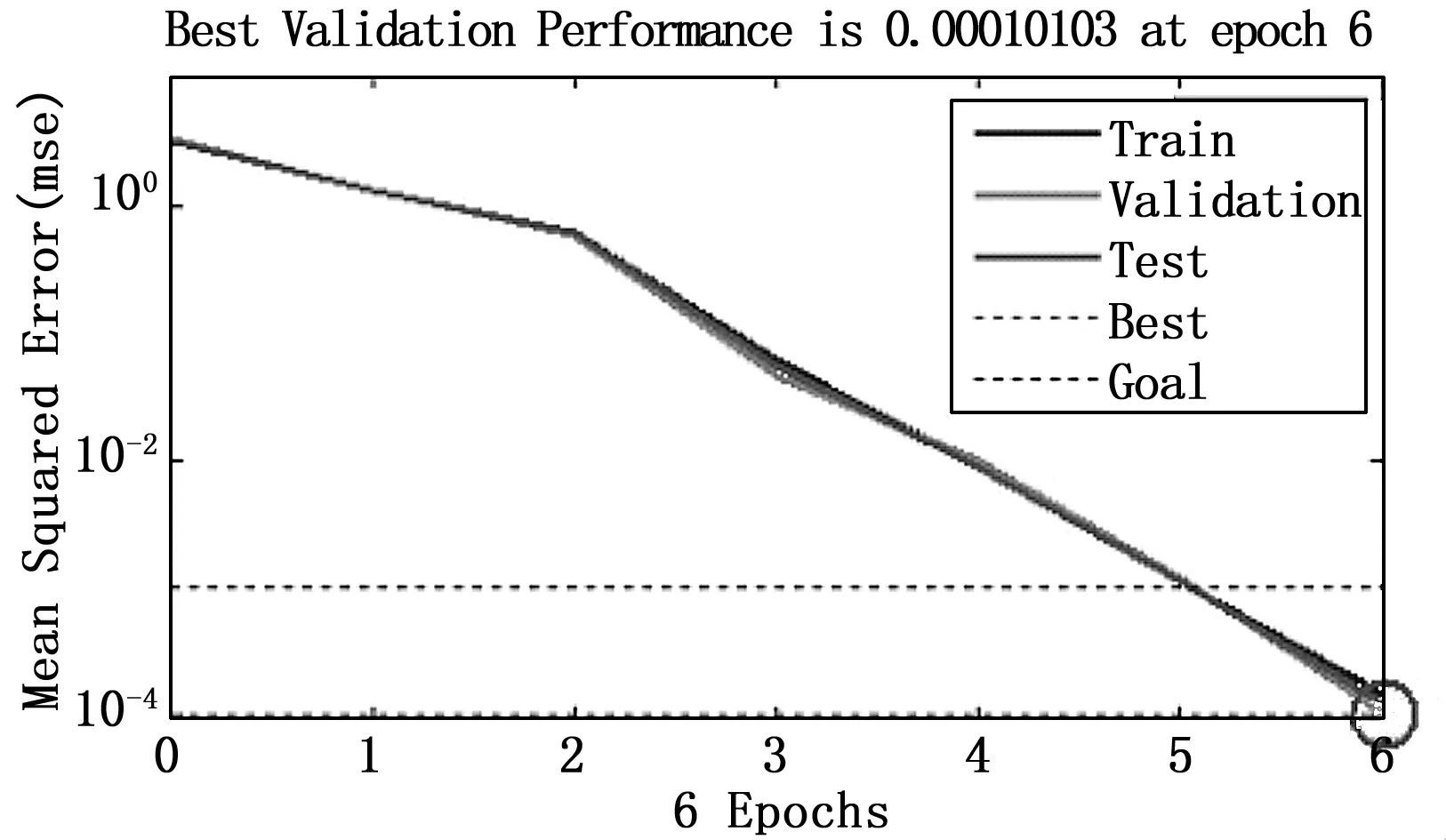
图4 网络训练误差曲线

图5 输出变量θ1的仿真曲线

图6 输出变量θ1的绝对误差
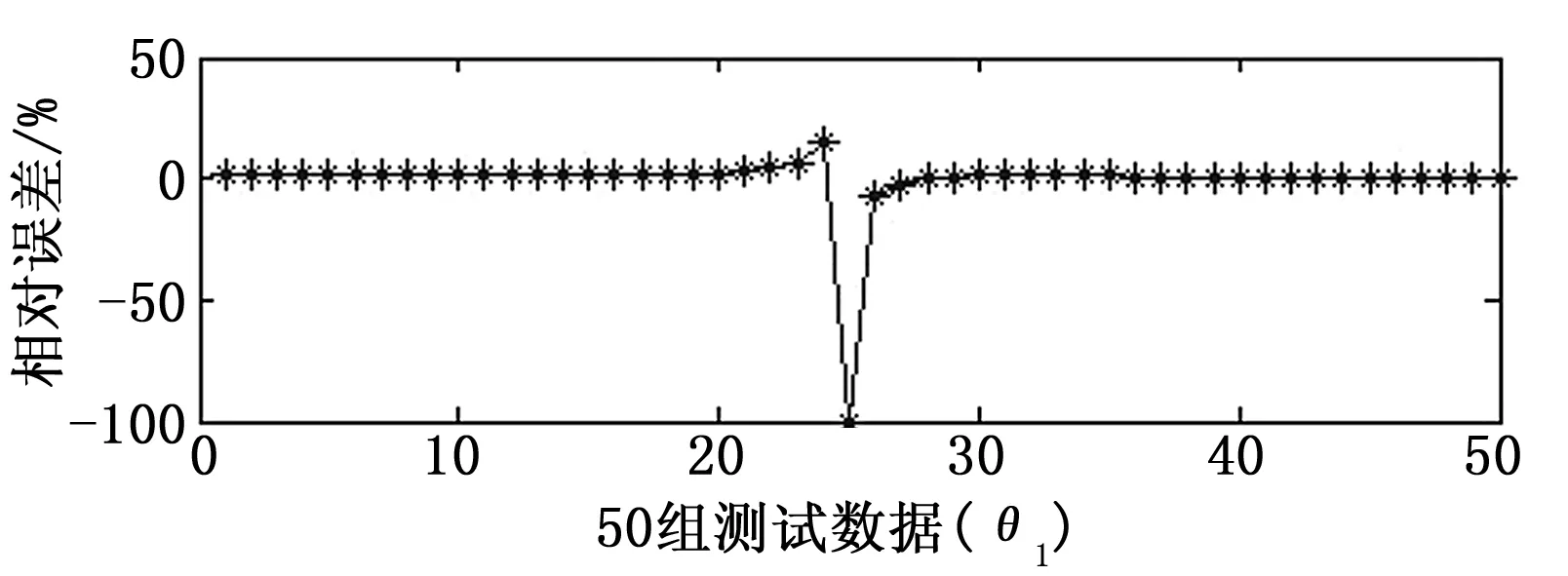
图7 输出变量θ1的相对误差
4 结论
文中基于BP神经网络提出一种机械臂逆运动学求解方法,并对神经网络的训练算法进行改进,最后使用MATLAB神经网络工具箱对该方法进行仿真验证,仿真结果表明该方法是可行的,并由仿真结果得出以下结论:不同的BP神经网络训练算法对仿真结果有较大的影响,不同算法得出的仿真结果差别显著,相比有其他3种方法,采用LM法的收敛速度较快,精度较高;神经网络采用LM训练方法时,改变不同的隐含层与输出层的神经元数组合对仿真结果的影响较小。文中采用改进算法的BP神经网络求解机械臂逆运动学具有较快的收敛速度和较高的求解精度,可以满足复杂机械臂逆运动学求解的需求。
[1]John J Craig. 机械臂学导论[M].北京:机械工业出版社, 2006.
[2]臧庆凯,李春贵. 基于3个并行BP神经网络的机器人逆运动学求解[J].计算机测量与控制, 2012,20(8):2244-2247.
[3]Paul R P,Shimano B E,Mayerg. Kinematics control equations for simple manipulators[J]. IEEE Transactions on Systems, Man and Cybernetics, 1981,11(6):445-449.
[4]Regnier S, Ouezdou F B,Bidaud P.Distributed method for inverse kinematics of all serial manipulators[J].Mechanism and Machine Theory,1997 ,32(7):855-867.
[5]Xu D,Calderon C A,Gan J Q. An analysis of the inverse kinematics for 5-DOF manipulator [J].International Journal of Automation and Computing, 2005,2(2):114-124.
[6]蒋宏超,刘士荣,张波涛。六自由度模块化机械臂的逆运动学分析[J].浙江大学学报(工学版),2010,44(7):1348-1354.
[7]李宪华,郭永存,张军,郭帅。模块化六自由度机械臂逆运动学结算与验证[J].农业机械学报,2013,44(4):246-251.
[8]刘晓玉,方康玲.基于神经网络的机械臂视觉伺服研究[J].计算机应用,2008(3):149159.
[9]孟庆鑫,王晓东.机器人技术基础[M], 哈尔滨:哈尔滨工业大学出版社,2006.
[10]刘冰,郭海霞. MATLAB神经网络超级学习手册[M].北京:人民邮电出版社, 2014.
[11]董长虹. MATLAB神经网络与应用[M]. 北京:国防工业出版社, 2007.
Inverse Kinematics Analysis of Anti-bomb Robot Based on BP Neural Network
Li Wenbo, Cao Bing, Zhang Yunbo
( School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing210094,China)
Manipulator inverse trajectory which means to solve the joint variable by the end of the mechanical arm position is mainly used in the accurate location and trajectory planning of the end executor. How to efficiently solve the inverse solution of kinematics of robotic is the difficulty. In view of the traditional algorithm of robot arm inverse kinematics is complex and there are multiple solutions, this paper proposes a mechanical arm inverse kinematics method based on BP neural network. With four degrees of freedom mechanical arm as the research object, analyses its kinematics principle, on the basis of improving the BP neural network algorithm, the mechanical arm are simulated and modeled by using MATLAB toolbox. The results show that using BP neural network model to solve inverse kinematics which avoids the disadvantages of traditional methods is simple in design and precision; it is a feasible manipulator inverse kinematics solution.
robot arm; inverse kinematics; neural networks; optimization algorithm
2015-07-19;
2015-08-28。
李文博(1988-),男,河南周口人,硕士研究生,主要从事机电一体化方向的研究。
曹兵(1967-),男,河南南阳人,副教授,硕士研究生导师,主要从事弹药工程与爆炸技术方向的研究。
1671-4598(2016)01-0207-05
10.16526/j.cnki.11-4762/tp.2016.01.057
TB183;TP242
B

