一维弹道修正弹飞行稳定性研究

吴汉洲，宋卫东，王　毅，张　磊，宋谢恩

(军械工程学院 火炮工程系，石家庄　050003)



一维弹道修正弹飞行稳定性研究

吴汉洲，宋卫东，王毅，张磊，宋谢恩

(军械工程学院 火炮工程系，石家庄050003)

为分析一维弹道修正弹阻力片不同修正能力下，其打开后对弹丸飞行稳定性的影响大小，以某型100 mm一维弹道修正弹为研究对象，运用Simulink软件建立了6自由度刚体弹道模型,通过设置不同仿真条件，利用阻力片打开后弹丸攻角变化、陀螺稳定性判据、动态稳定性判据判断弹丸飞行稳定性;求出了在阻力片分别产生原来弹丸阻力系数3倍、4倍、5倍阻力下，为保证弹丸飞行稳定应控制阻力片打开后产生的新的静力矩的极限值应分别小于原弹丸静力矩的3倍、3.5倍、4倍;通过研究阻力片打开时间对弹丸飞行稳定性的影响，结果表明，阻力片打开时间越晚其对弹丸飞行稳定性的影响越大；分析了阻力片一定修正能力下，以不同射角射击时为保证阻力片打开后弹丸飞行稳定性，阻力片最晚打开时间。

一维弹道修正；弹道建模；稳定性；修正能力

0　引言

随着科技的进步，精确制导武器在作战中使用频率不断升高，从海湾战争到伊拉克战争，战争中精确制导武器占总投弹量由8.36%提升到68%。弹道修正弹只改进常规弹药的引信，在改造成本不高的情况下能使射击精度成倍提高，近年来成为各国研究的热点[1-2]。

一维弹道修正弹在飞行中通过增加轴向空气阻尼进行射程上的修正，增加阻尼的方式主要是在弹头部弹出阻力片(环)。文献[3]从阻力环安装位置及展开面积入手，分析了阻力环对弹丸阻力系数、升力系数、俯仰力矩系数及压心系数的影响。文献[4]以一维弹道修正弹伞形阻力器为核心，在分析该阻力器对弹丸阻力系数等的影响基础上，通过数值模拟分析得出了阻力伞展开角度、修正时刻等因素与弹丸修正距离之间的规律。文献[5]以某型57 mm弹丸为研究对象，利用Fluent流体仿真软件，获得了弹丸在不同马赫数、阻力片不同展开高度、不同展开时刻及作用时间情况下的气动力参数，并通过外弹道程序验证了阻力环的增阻效果。从目前发表文献来看，研究者研究内容主要侧重于阻力片(环)打开后弹丸飞行稳定性及对射程的修正量等，而对阻力片(环)打后对弹丸飞行稳定性影响大小鲜有研究。

本文通过弹道建模、仿真模拟等分析了阻力片在不同修正能力下阻力片打开后对弹丸陀螺稳定、动稳定、追随稳定的影响大小；分析了弹丸飞行不同时刻打开阻力片对弹丸飞行稳定性的影响等。

1　弹道建模及稳定性判据

1.1弹道微分方程组

本文参阅文献[6-7]，使用Simulink软件建立了某型100 mm一维弹道修正弹刚体弹道模型。鉴于该弹为小射程近距离杀伤武器，模型忽略了地球表面曲率、弹丸质量偏心等对弹丸飞行的影响。弹道方程组如下，相关变量定义参阅文献[6]。

(1)

图1、图2分别为在射角为15°、30°、45°时弹丸飞行弹道曲线和攻角变化曲线。仿真结果显示该弹道模型能够客观反映弹丸弹道特性，且具有较好的仿真精度。

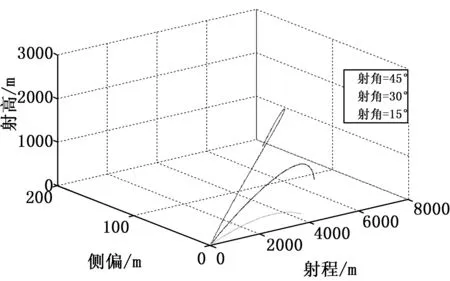
图1　不同射角下弹道曲线图

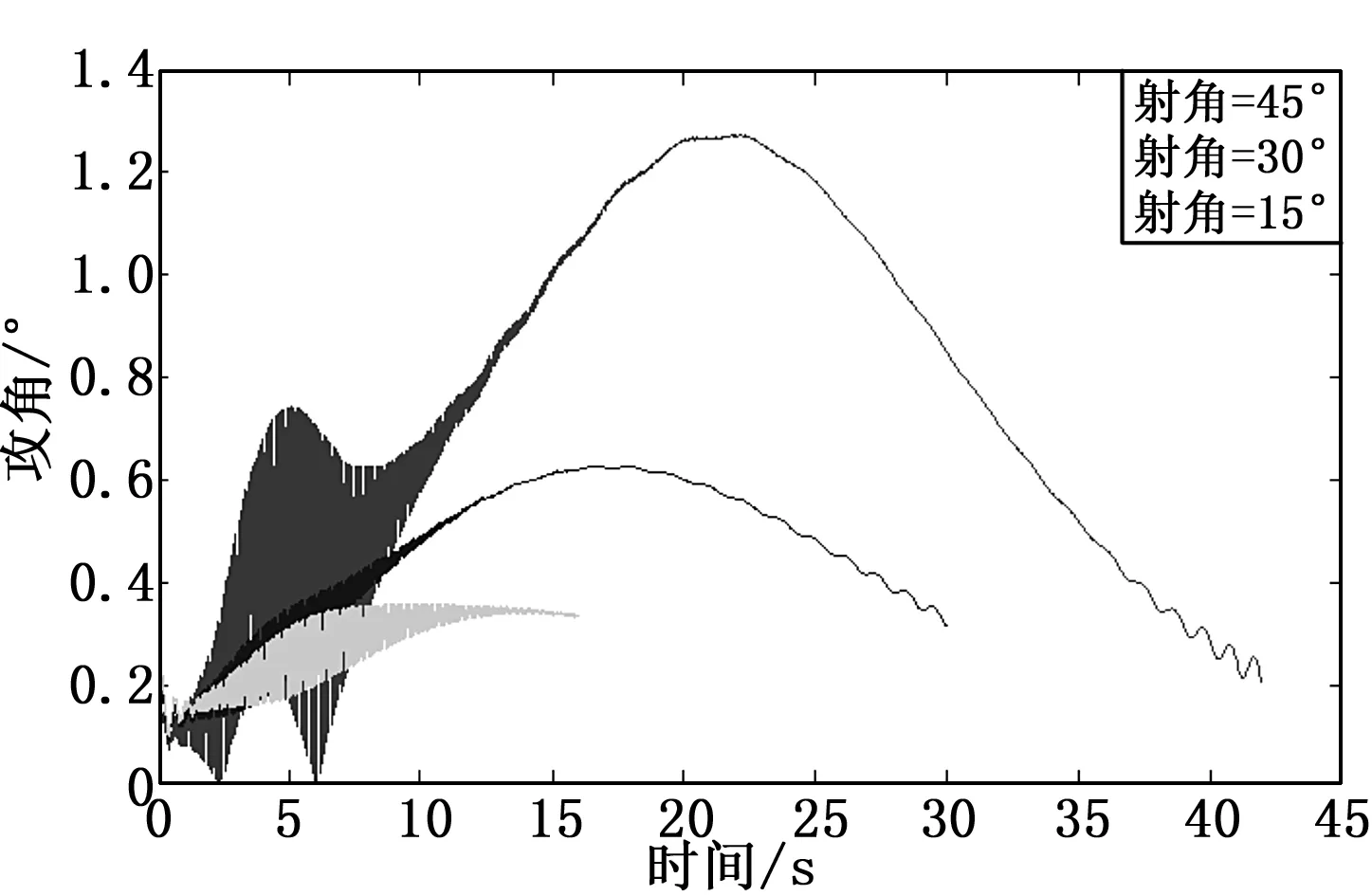
图2　不同射角下弹丸攻角曲线图

1.2稳定性判据[6]

1.2.1陀螺稳定性判据

(2)

为陀螺稳定因子，其中M为弹丸受到的静力矩，当Sg≥1.3时弹丸具有陀螺稳定性。

1.2.2动态稳定性判据

仅满足陀螺稳定性判据的弹丸，在飞行中虽能稳定飞行，但其攻角幅值可能会一直较大，特别当弹丸飞行中受到一定扰动出现攻角震荡时，弹丸攻角会一直震荡下去，而同时满足动态稳定性的弹丸，飞行中在攻角阻尼作用下，攻角幅值会趋于减小，攻角震荡减弱。通常定义

(3)

(4)

1.2.3追随稳定性判据

动力平衡角过大会影响弹丸射程，增大落点散布，甚至出现弹底着地，引信不起爆现象。动力平衡角最大值出现在最大射角射击时的弹道顶点附近，只要该值小于限制值δpm则认为弹丸具有追随稳定性。对于右旋弹丸只考虑静力矩时的动力平衡角为

(5)

2　不同修正能力的阻力片打开后对弹丸飞行稳定性影响

2.1仿真条件设置

一维弹道修正弹在打开阻力片(环)时，弹丸引信气动外形瞬间发生变化，弹丸质量、质心、转动惯量等变化较小，可以乎略；但弹丸轴向空气阻力成倍增大，弹丸压心前移，静力矩增大，弹丸飞行稳定性减弱。因此在分析不同修正能力的阻力片打开后对弹丸飞行稳定性影响时，只考虑弹丸轴向空气阻力及静力矩对弹丸飞行稳定性影响即可。本文以某型100 mm一维弹道修正弹为例，阻力片增阻倍数设置值为该型号修正弹方案设计中采用的数值，在一维弹道修正弹方案设计中，为保证飞行稳定性阻力片打开后增大的静力矩应小于某极限值，本文设置的仿真数值比实际值偏大，用以求解出该极限值。在作者前期的研究中，阻力片产生不同增阻能力、不同静力矩条件下，在不同射角下，弹丸飞行稳定性变化规律基本相同，限于篇幅，本文以36°射角为例进行仿真说明。阻力片打开时间为14 s条件下设置如表1仿真试验。

表1　阻力片不同修正能力下仿真试验表

2.2仿真结果及结论

仿真结果如图3～12所示。

从图3～5可看出在同时增大阻力系数和静力矩情况下弹丸飞行稳定性降低，特别当产生原来4倍静力矩时，弹丸攻角会急剧增大，失去飞行稳定性。根据陀螺稳定判据及动稳定判据要求，从图中可看出，在阻力片产生3倍原来弹丸阻力系数情况下，应控制阻力片张开产生增大的静力矩小于原来弹丸静力矩的3倍才能保证弹丸飞行稳定。弹丸追随稳定性曲线显示阻力片打开能进一步增加弹丸飞行追随稳定性，限于篇幅文中不再画图讨论。

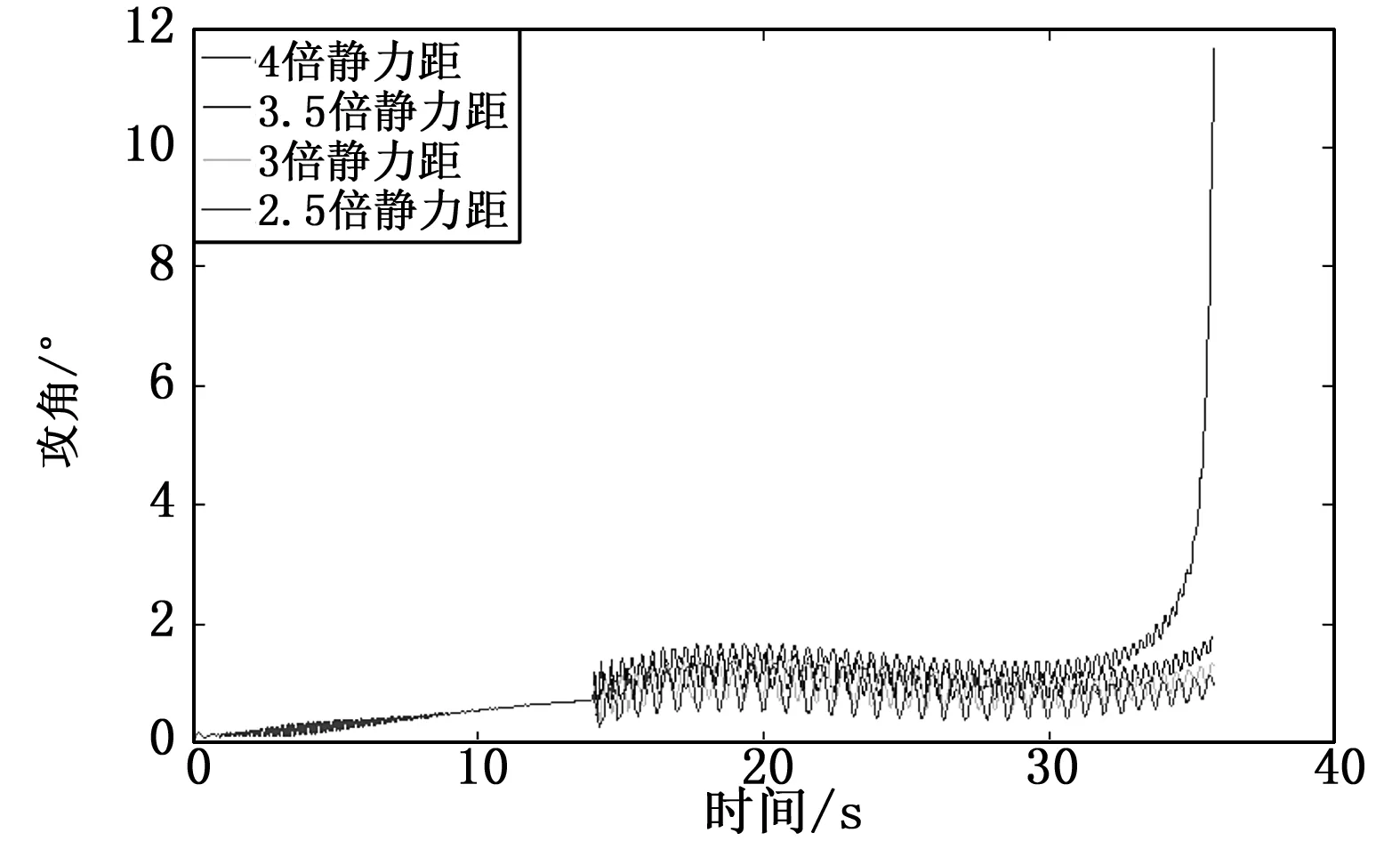
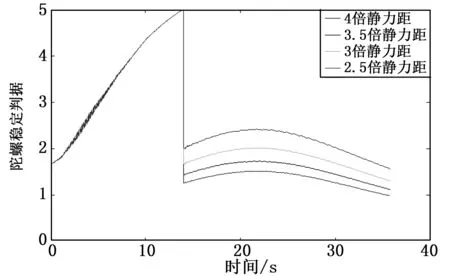
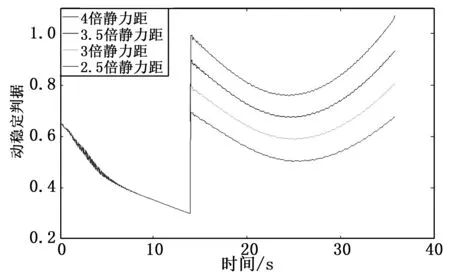
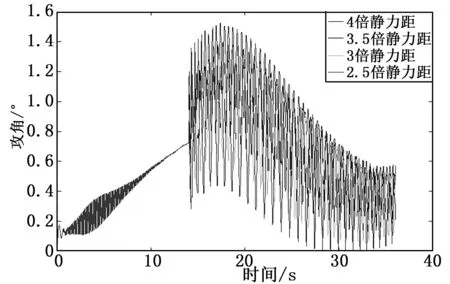
图3阻力片产生原弹丸3倍阻力、不同静力矩下攻角变化曲线

图4阻力片产生原弹丸3倍阻力、不同静力矩下陀螺稳定性曲线

图5阻力片产生原弹丸3倍阻力、不同静力矩下动稳定性曲线

图6阻力片产生原弹丸4倍阻力、不同静力矩下攻角曲线

比较图6和图3可看出，在产生相同静力矩不同增阻系数下，阻力片产生4倍增阻系数引起的攻角震荡比3倍的要大，但攻角增大是有限的，仍可认为弹丸飞行是稳定的

[9]

。在阻力片产生4倍增阻系数产生原弹丸4倍静力矩情况下打开阻力片后已不能满足弹丸飞行陀螺稳定性，阻力片打开瞬间也不能满足动稳定性。从图中可看出，在阻力片产生4倍增阻系数情况下，应控制其打开后产生的增大的静力矩不大于弹丸原来静力矩的3.5倍。

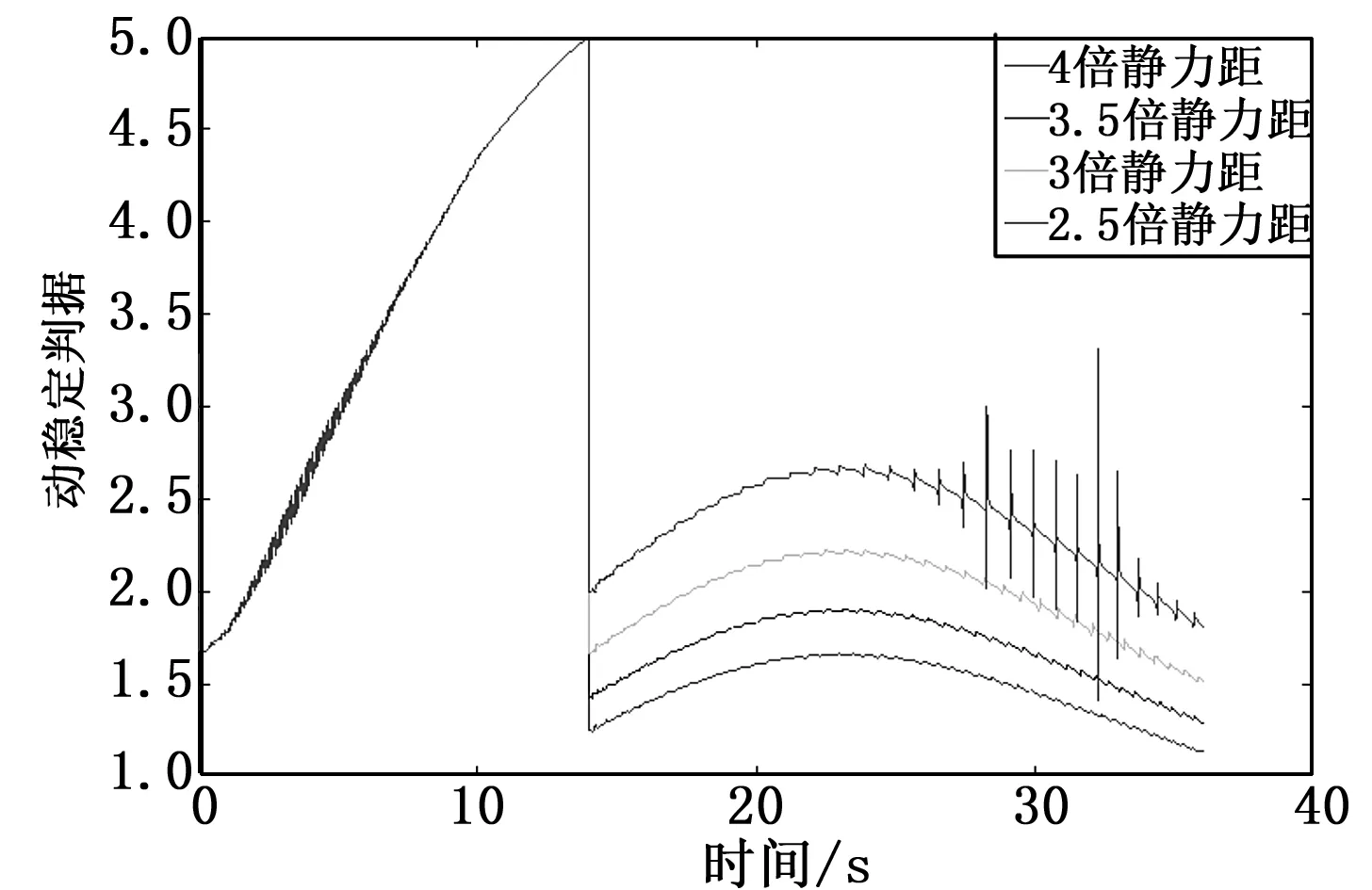
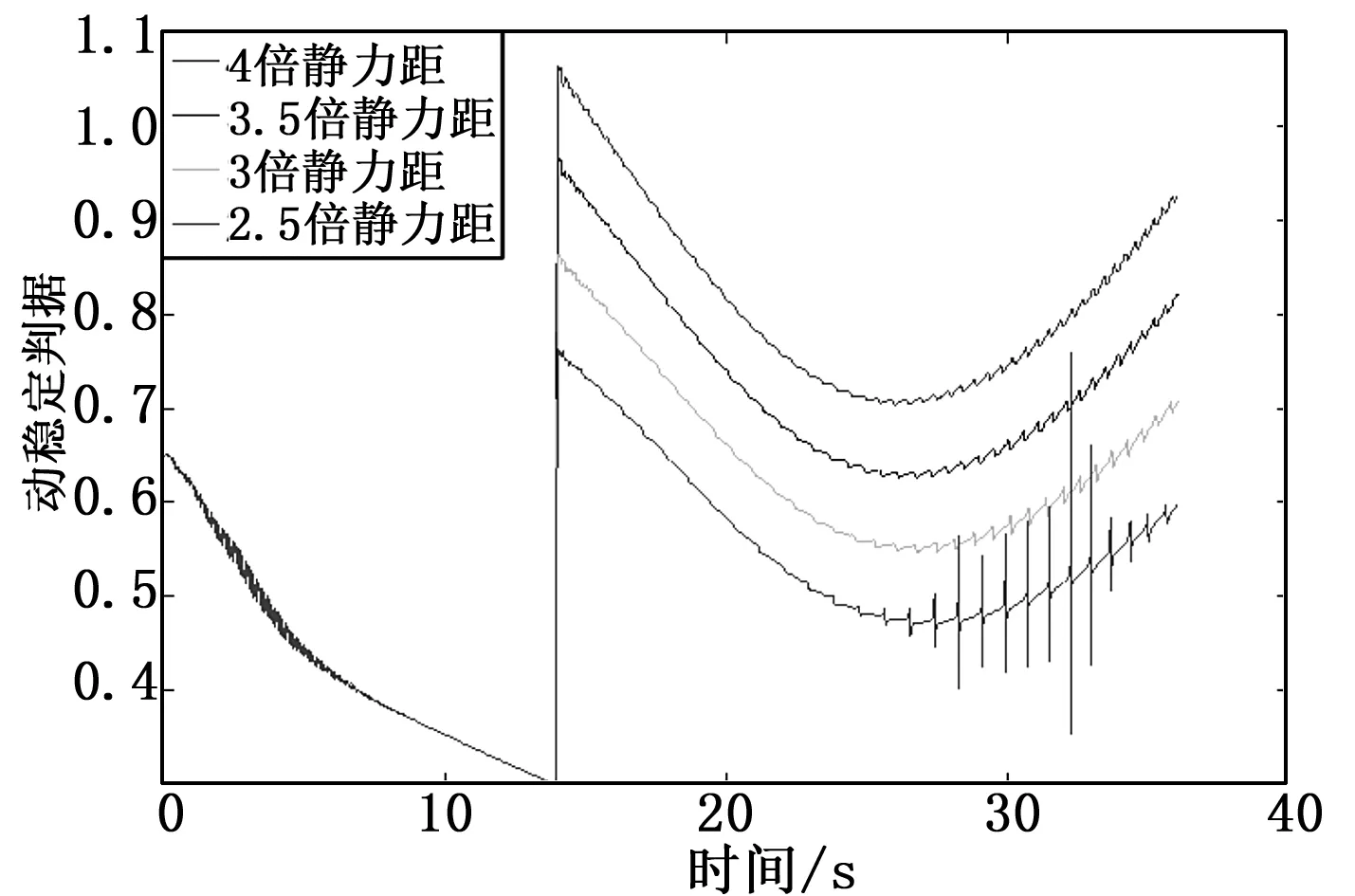
图7阻力片产生原弹丸4倍阻力、不同静力矩下陀螺稳定性曲线

图8阻力片产生原弹丸4倍阻力、不同静力矩下动稳定性曲线

比较图9～11与图6～8可看出，不仅弹丸飞行过程中攻角出现较大幅值震荡，陀螺稳定性曲线、动稳定性曲线也开始出现数值跳动，说明在阻力片产生大阻力系数下，弹丸飞行稳定性降低明显。从图9～11可看出，在阻力片产生5倍增阻系数下，应控制其打开后产生的增大的静力矩小于原来弹丸飞行静力矩的4倍。

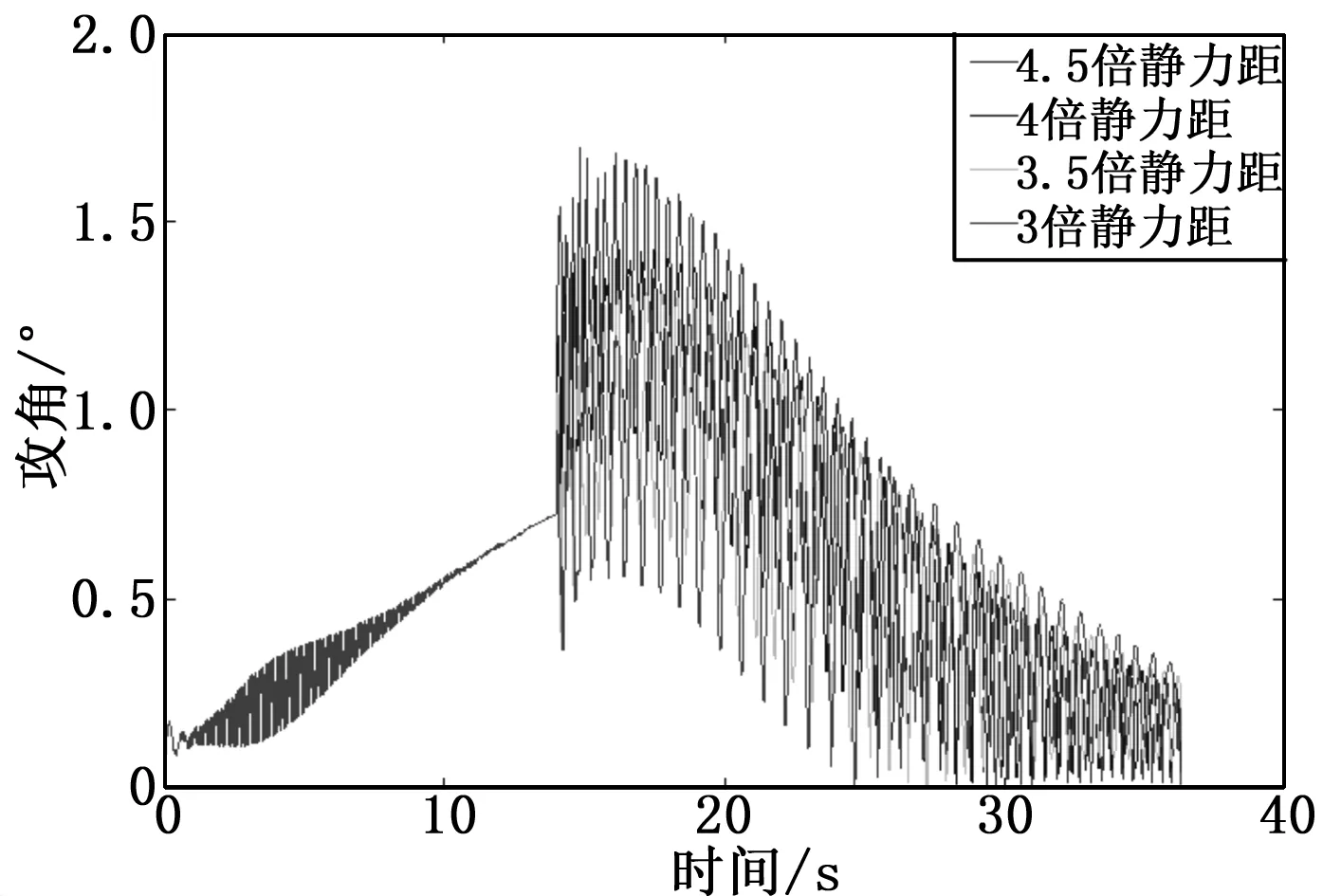
图9阻力片产生原弹丸5倍阻力、不同静力矩下攻角曲线

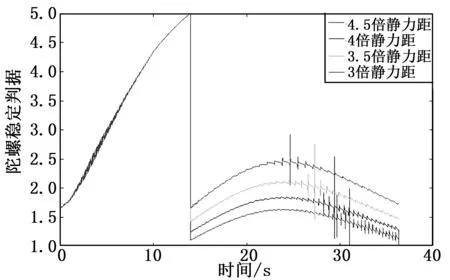
图10阻力片产生原弹丸5倍阻力、不同静力矩下陀螺稳定性曲线

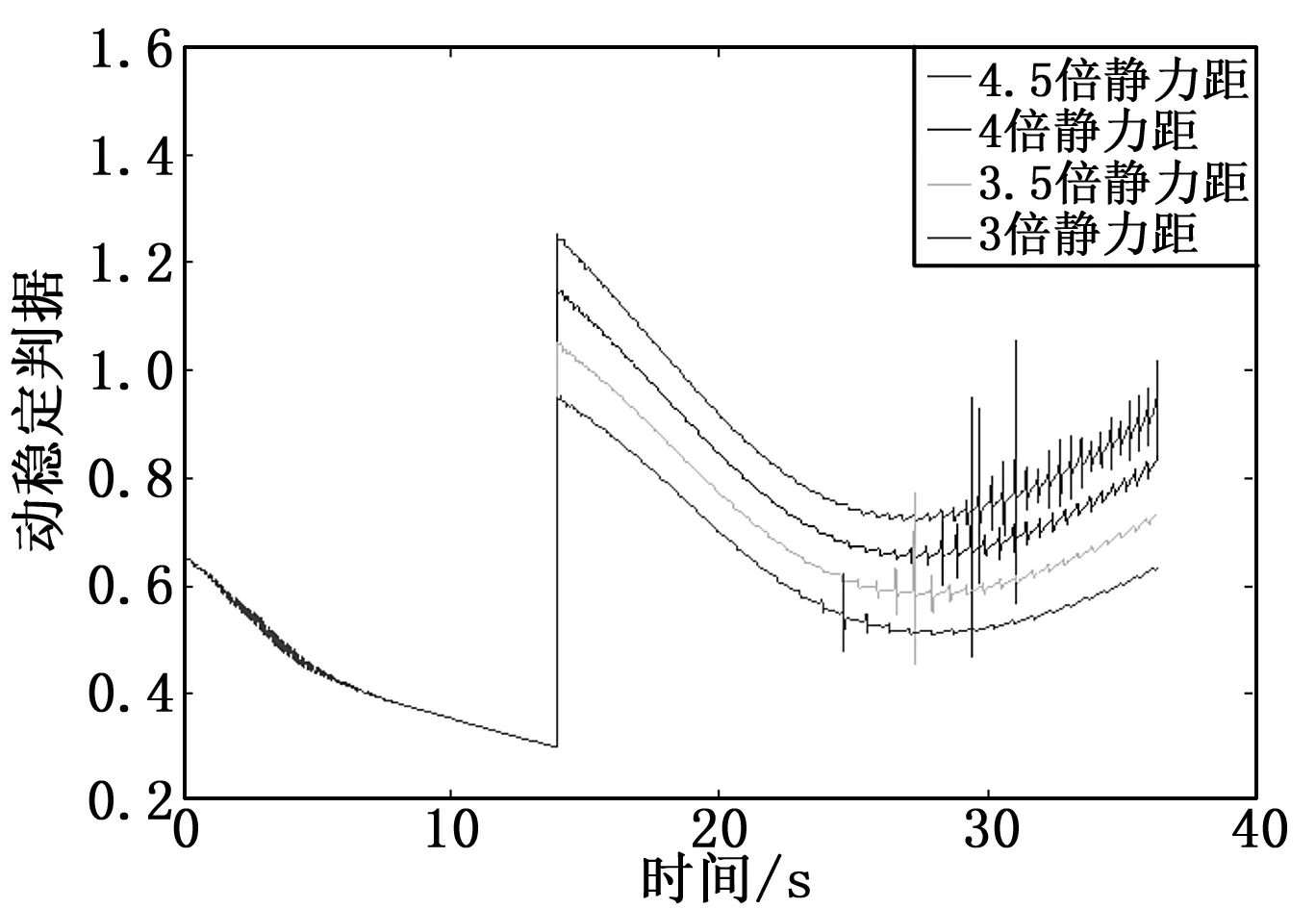
图11阻力片产生原弹丸5倍阻力、不同静力矩下动稳定性曲线

3　阻力片不同打开时刻对弹丸飞行稳定性的影响

3.1仿真条件设置

在研究弹丸飞行稳定性问题时，弹丸出炮口时间段、弹道顶点时间段及弹丸落地前时间段等常作为研究其飞行稳定性的重点。本文以某型100 mm一维弹道修正弹为例，以阻力片产生4倍原来弹丸阻力系数、2.5倍原来弹丸静力矩，36°射角射击(弹丸飞行时间为35.09 s，弹丸到达弹道顶点时间为17.2 s)为基本条件，设立如表2仿真试验。

表2　阻力片打开时刻表

3.2仿真结果及结论

仿真结果如图12～14所示。

从图12～14可看出，阻力片打开时间对弹丸飞行稳定性影响较大。阻力片打开越晚对弹丸飞行稳定性影响越大，特别是在32 s打开时，弹丸攻角开始不断增大，弹丸飞行也已不满足陀螺稳定性，这主要是因为到了弹道末期弹丸自转转速下降较多，产生的陀螺稳定性已不能维持阻力片打开时产生的扰动。为保证弹丸飞行稳定性，在该仿真条件下，应保证阻力片打开时间不晚于26 s(即弹丸自转角速度不小于560 rad/s)。图15为在该仿真条件下，不同射角射击时为满足弹丸飞行稳定性阻力片最晚打开时间曲线图。

图12　阻力片不同打开时刻弹丸攻角变化曲线

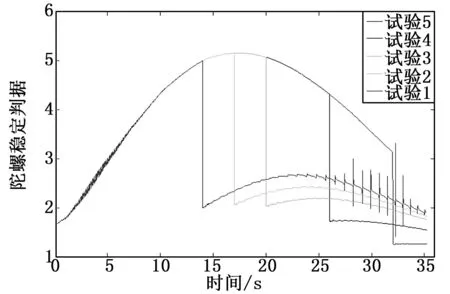
图13　阻力片不同打开时刻弹丸陀螺稳定性曲线

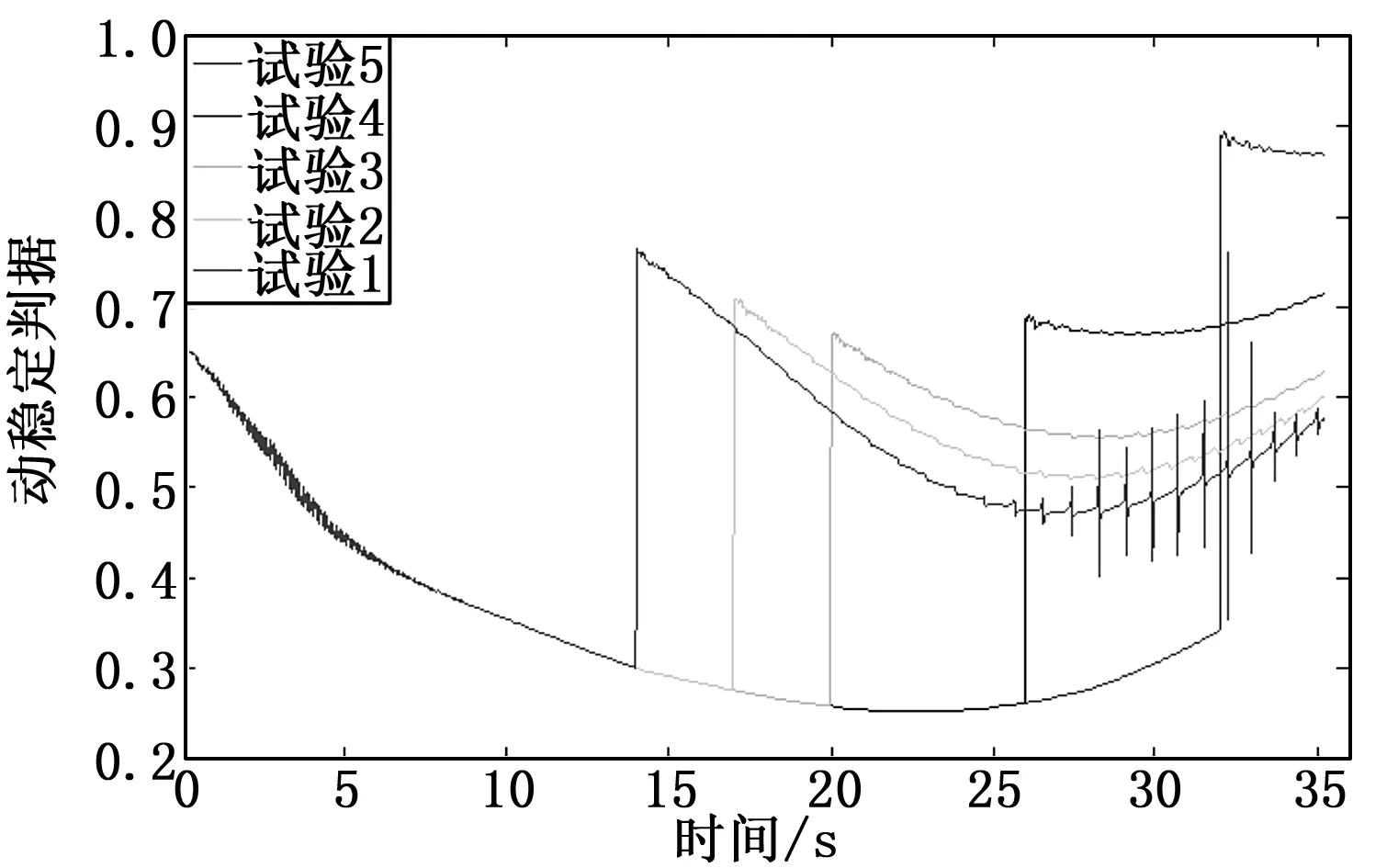
图14　阻力片不同打开时刻弹丸动稳定性曲线

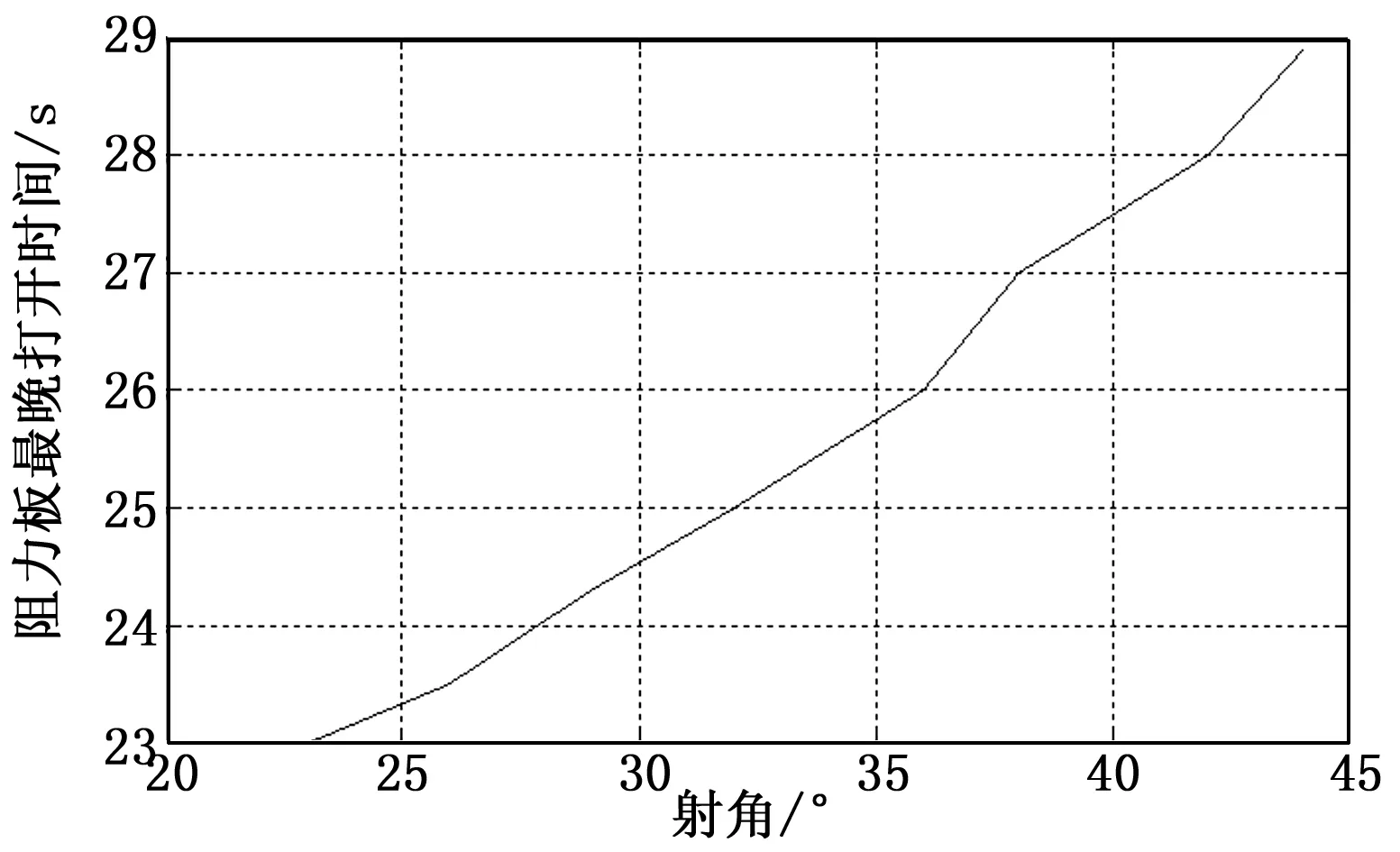
图15　不同射角下阻力片最晚打开时间图

4　结论

本文以某型100 mm一维弹道修正弹为例，分析了阻力片不同修正能力下打开后对弹丸飞行稳定性的影响大小。仿真结果表明，在阻力片分别产生原来弹丸阻力3倍、4倍、5倍阻力下，应通过调整阻力片安装位置或外形等使其产生的静力矩分别小于原来弹丸静力矩的3倍、3.5倍、4倍。通过研究阻力片打开时间对弹丸飞行稳定性的影响，结果表明，阻力片打开时间越晚其对弹丸飞行稳定性的影响越大，进而分析了在阻力片产生4倍原来弹丸阻力系数、2.5倍原来弹丸静力矩情况下为保证阻力片打开时弹丸飞行稳定性，在不同射角下阻力片最晚打开时间。本文研究思路及内容为一维弹道修正弹修正机构外形设计及修正机构最晚开启时间等具有一定的参考意义。

[1]陈科山, 马宝华, 何光林, 等. 一维弹道修正引信阻力器的研究现状分析及其设计原则探讨[J]. 探测与控制学报, 2003, 25(3)：24-29.

[2] 谭凤岗. 弹道修正弹的概念研究[J]. 弹箭技术, 1998, (4)：1-10.

[3] 裔萍. 一维弹道修正弹的气动力特性研究[D]. 南京：南京理工大学, 2006.

[4] 吴雪飞. 一维弹道修正弹刚性伞形阻力器气动特性分析[D].太原：中北大学, 2013.

[5] 徐永杰, 吴国东, 刘强, 等. 增阻式一维弹道修正弹气动分析[J]. 弹箭与制导学报, 2013, 33(6), 133-136.

[6] 韩子鹏, 等. 弹箭外弹道学[M]. 北京：北京理工大学出版社, 2008.

[7] 李文清, 符文星, 闫杰, 等. 某型导弹几种典型干扰的建模与仿真[J]. 计算机测量与控制, 2011, 19(8)：932-1935.

[8] 宋丕极. 枪炮与火箭外弹道学[M]. 北京：兵器工业出版社, 1993.

[9] 董亮, 王宗虎,赵子华, 等. 弹箭飞行稳定性理论及其应用[M]. 北京：兵器工业出版社, 1990.

Research of Stability of Flight of One Dimension Trajectory Correction Projectile

Wu Hanzhou，Song Weidong，Wang Yi，Zhang Lei，Song Xieen

(College of Ordnance Engineering ，Shijiazhuang050003，China)

To a certain type of one dimension trajectory correction projectile as the research object, six DOF rigid body model is established. By setting different simulation conditions, the stability of the projectile before and after the damper opens is analyzed by the angle of attack, gyroscopic stability criterion and dynamic stability criterion. The influence of the damper which is in different correction ability to the projectile flight stability when it opens is analyzed. In order to ensure the flight stability the limit value of the static moment are 3 times, 3.5 times, 4 times as much as original static moment when damper opens when damper produces 3、4、5 times as much resistance coefficient as original projectile. Analyzed the influence of the damper starting time to the stability of the projectile flight. The simulation results show that the later of the damper is opened the greater impact to the projectile flight. The latest open time is analyzed of the damper in a certain correction ability.

one dimension trajectory correction；trajectory modeling；stability；correction capability

2015-07-02；

2015-09-06。

吴汉洲(1989-)，男，山东日照人，硕士研究生，主要从事弹箭弹道理论与应用技术研究方向的研究。

1671-4598(2016)01-0132-05

10.16526/j.cnki.11-4762/tp.2016.01.037

TJ012.3

A