基于经济损失的风险优先值排序方法研究及应用

关玉明, 刘慧娟, 刘　琴, 王锡瑞, 许　波

(河北工业大学 机械工程学院, 天津 300130)



基于经济损失的风险优先值排序方法研究及应用

关玉明, 刘慧娟, 刘琴, 王锡瑞, 许波

(河北工业大学 机械工程学院, 天津 300130)

针对传统失效模式和影响分析(FMEA)中风险优先等级(RPN)分析方法存在的离散性、重复性，以及灵敏度低、准确性差等缺陷,提出了一种基于经济损失的风险优先值排序方法——ERPN(risk priority number ranking method based on the economic losses).该方法采用定性与定量相结合的方式,首先确定某潜在失效情景的严重度,然后根据相关数据确定某初始事件发生概率以及此潜在失效情景所导致的经济损失,用两者的乘积作为ERPN值.该方法直接可观,可操作性强,具有较好的工程实用性.将其与基于反向鱼骨图的结构分解、基于情景的失效分析相结合,综合应用在自动包装生产线的送膜包覆装置的失效分析中,取得了很好的效果.

失效分析; 经济损失; ERPN排序方法; 反向鱼骨图; 工程实例

随着现代机械结构复杂程度的提高,机械产品的可靠性要求也逐渐提升,而失效分析作为可靠性研究的重要方法,在机械产品的设计中也成为必不可少的一环.失效模式和影响分析(FMEA)是目前比较常用的失效分析方法之一,该方法在分析某种特定产品或者某个特定系统时,首先用头脑风暴方法识别出产品或系统所有可能的失效模式,然后对产品或系统的失效模式进行优先顺序排序,从而将有限的资源分配给最危险的风险项,即传统的RPN方法.但传统排序方法是根据故障模式的严重度(S)、发生频度(O)、检测难易程度(D)三者的乘积作为RPN值,此计算方法虽然直观易懂,但从技术层面上分析,S，O，D是三个从1到10的数值,简单相乘得到的结果存在较大的误差.

许多学者采用不同的评定准则对传统FMEA方法中的RPN排序方法进行了修正和补充,主要分为多准则决策(MCDM)、人工智能(AI)、数学规划(MP)、混合算法和其他方法这几类,具体来说,应用较为广泛的依次为模糊规则库方法、灰色理论、基于费用模型、层次分析法/网格分析法(AHP/ANP)、线性规划等.Liu Hu-chen等人对1992—2012年间有关FMEA中风险评估方法的相关文献进行了综述[1],并在之后根据风险因素的不确定性和机械系统的复杂性提出多种改进方法,如模糊环境下扩展的全乘比例分析多目标优化方法(MULTIMOORA)、灰色关联映射方法、组合加权和模糊VIKOR相结合的方法、模糊加权均值和模糊决策试验与评价实验室(DEMATEL)相结合的方法等[2-5],这些方法多基于模糊理论,其局限性在于难于定义风险因素和优先级别的隶属函数,难于设计合适的软件来实现风险输入和输出之间的即时通信等;Bowles[6]在对传统方法分析的基础上提出以费用期望值作为RPN排序依据,但未提出具体实现方法;陈政平等[7]通过定性和定量分析提出一种基于费用和发生概率的分析方法；晋民杰等[8]以时间、损失金额等定量因素替代传统方法中的严重度、频率和检测难易度这3个参数进行计算,也提出基于费用的排序方法,但两者均未深入涉及自动生产线中的工艺过程.笔者结合包装生产线中工艺要求,提出一种基于经济损失的排序方法,并将其与基于反向鱼骨图的结构分解、基于情景的失效分析相结合,在一个工程实例中进行了验证.

1　传统的RPN

1.1传统RPN的应用流程

传统FMEA是根据RPN值的大小判断是否有必要进行改进或确定改进的程度,减少事后损失,提高系统的可靠性.RPN值由故障模式的严重度(S)、发生频度(O)、检测难易程度(D)决定,即RPN=S×O×D,S一般分为灾难的、致命的、临界的、轻度的等10个等级,O一般可分为极高、高、中等、低等10个等级,D一般分为极难、难、可能、能等10个等级.传统RPN应用模型如图1所示.

图1　传统RPN应用流程图Fig.1　Flow chart of traditional RPN application

1.2传统RPN的缺陷

1.2.1RPN值的重复性与离散性问题

3个参数,每个参数取值有10种,因此S，O，D总共有1 000种组合,但它们乘积只有120种,因此这里面存在着很多的重复[9],比如24=2×3×4=3×4×2=2×2×6=…，虽然这几种组合的RPN值相同,但(2,3,4)，(3,4,2)，(2,2,6)隐含的风险却是不同的.此外,由于只能得到120个取值,那么88%的数字是得不到的,比如65～69这些数字无法得到,那么数字之间就会存在断层,因此数值不连续[10],这就很难解释RPN差值所代表的含义.

1.2.2RPN值的准确性与灵敏度问题

对于为什么采取3个参数乘积的结果作为RPN值,至今没有任何原理来支撑这个公式[11],且参数S和D都是采用语言描述,这本身就存在很大的不确定性,例如S取7,O取8,一个分析者认为D取5,另一个分析者认为D取6,那么结果分别为280和336,由于D受主观因素影响较大而导致这2个结果有较大的差距.由上又可知,由于RPN值是3个参数相乘的结果,1个参数微小变化的影响会被放大,如果评估不当,一些关键的故障模式可能无法被发现[12].

1.2.3RPN值的权重衡量问题

传统的RPN值的计算认为3个参数S，O，D具有相同的重要性,也就是忽视了3个参数权重的不同[13],但事实上严重度S和发生频度O应该优先分析,例如2个部件的RPN值相同,都为80,其中RPN1=8×5×2,RPN2=8×2×5,用于纠错的优先权应是第1个,因为第1个部件的失效概率要比第2个大得多.

此外,传统RPN值还存在着诸如难以评估改进措施的有效性，未考虑各种失效模式之间的相互依赖性，只考虑了安全性、没有考虑到经济性等问题[14-15],在工程实际的应用中往往出现相对于实际情况的失真.

2　基于经济损失的风险优先值

2.1公式解读

为了减少传统RPN值计算时的主观性干扰,进一步提高风险优先级排序的可信度,采用从参数量化的角度将语言描述量以工程实践中收集到的可观实际数据来代替.首先按照传统RPN分析方法的严重度S对系统各工序步骤潜在的失效模式对系统和人员、环境等造成影响的严重程度进行分析和评价,对S≥9的不再进行分析,直接认定该失效模式应该重新设计、更换组件或者实行其他改进措施.

对于严重度S<9的,采取如下公式计算:

ERPN(Si)=P(Si)×E(Si)，

(1)

其中：ERPN(Si)为基于经济损失的失效风险优先值;P(Si)为失效情景发生的概率;E(Si)为该失效最终导致的经济损失.

2.1.1失效模式的概率分析P(Si)

设一个事件的成功情景为S0,违背这一成功情景的失效情景为Si,导致该失效情形的初始事件为IEi,则初始事件与失效情景间的关系如图2所示.

图2　初始事件与失效情景的关系Fig.2　Relationship between initial events and failure scenarios

1)若单独的初始事件导致了失效情景的发生,如逻辑关系(a),则

P(Si)=P(C1)，

(2)

其中：P(Si)为该失效情景发生的概率；P(C1)为导致该失效情景的初始事件发生的概率.

2)若2个或2个以上的初始事件共同导致了失效情景的发生,即逻辑关系为“与”,如图(b),则该失效情景发生的概率为引起该失效的几个初始事件概率的乘积,即

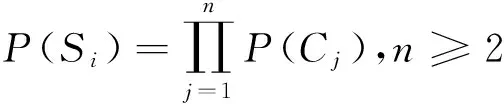
(3)

其中：P(Si)同上；P(Cj)为导致该失效情景的第j个初始事件发生的概率.

3)若2个或2个以上初始事件的任何一个都将导致失效情景的发生,即逻辑关系为“或”,如图(c),则该失效情景发生的概率为

(4)

其中P(Si)，P(Cj)的含义同上.

2.1.2失效模式的经济损失分析E(Si)

对于工程上而言,由初始事件导致的失效情景造成的经济损失包括三部分:产出损失E1、故障维修费用E2，以及故障导致的生产用原材料损失E3,即

E(Si)=E1(Si)+E2(Si)+E3(Si)，

(5)

其中,

E1(Si)=η×t×Vp，

(6)

其中：η为被分析系统的生产效率;t为失效造成的生产停滞的时间；Vp为系统所生产的单个产品的产值.

E2(Si)=Cm+C1，

(7)

其中：Cm为故障消除或生产恢复需要的材料费用；C1为故障消除或生产恢复需要的人工费用等.

E3(Si)=Wm+Wr，

(8)

其中：Wm为失效情景造成的生产材料损失；Wr为除此之外的其他损失.

2.2ERPN应用步骤

经过上述分析,论文提出的ERPN失效排序方法,可按以下几个步骤进行:

1)借助反向鱼骨图,按照工艺路线对某系统结构进行分解,并确定该系统潜在的失效模式;

2)确定各失效模式的严重度等级S的值;

3)对于严重度为9和10的失效模式,直接将其列为重要失效模式,需要采取设计或制造、装配上的措施予以纠正;

4)对严重度小于9的失效模式,首先分析初始事件与失效模式的逻辑关系,并以此确定P(Si),然后分析失效模式造成的经济损失E(Si);

5)根据上述P(Si)，E(Si)的值计算ERPN(Si)的值;

6)根据ERPN(Si)值的大小进行风险优先级排序,并选出重要的失效模式.

3　工程实例应用

笔者采用大型卷状包装生产线上的送膜包覆装置(如图3所示)来进行说明.首先采用反向鱼骨图按照工艺路线进行结构分解,然后根据各部分的功能判断可能的失效情景,再根据ERPN的计算公式计算出每一种失效模式的ERPN值,最后再进行排序.

1—拨料臂;2—热合切刀;3—平行板;4—包覆臂;5—拉料传动胶轴;6—无纺棉大卷;7—落料臂.图3　送膜包覆装置示意图Fig.3　Structure of membrane sending and packing device

1)送膜包覆装置的反向鱼骨图如图4所示.

图4　送膜包覆装置的反向鱼骨图Fig.4　Reverse fishbone diagram of membrane sending and packing device

2)根据分解的结构分析各功能步骤可能的失效情景，见表1.

表1　各功能步骤的潜在失效情景及严重度

3)计算各失效模式的ERPN值.

失效情景1-①发生的初始事件为位置误差累积,则失效情景1-①发生的概率等于初始事件发生的概率——位置误差累积发生的概率.考虑到齿轮传动副的间隙,失效情景1-①的概率可计算为

P(S1)=P(C1)=0.03.

分析该装置的工艺流程,再考虑系统不会停车,产品虽可用,但性能未达到理想状态.为了减少位置的累积误差,可以加编码器作为位置反馈,形成回路纠正误差,此种失效情景的经济损失可以计算为:

E1(S1)=η×t×Vp=0元，

E2(S1)=Cm+C1=405元，

E3(S1)=Wm+Wr=105元，

E(S1)=E1(S1)+E2(S1)+E3(S1)=510元.

因此,此失效情景1-①的ERPN值为

ERPN(S1)=P(S1)×E(S1)=15.30元.

失效情景3的严重度为10,直接作为重要的失效模式重新设计该部分的结构.对于失效情景5,严重度为4,对系统以及性能影响较小,可以不作为重要失效模式.接下来按照同样的计算方法对失效情景1-②、失效情景2、失效情景4、失效情景6进行一一计算,并将最后的计算结果列入表2.

表2　各功能步骤ERPN值排序

按照ERPN值的大小进行排序,排序结果如表2所示,选取风险优先值大于100元的为重要失效模式,因此筛选出3(落料臂摆动)、2(拨料臂摆动)、1-②(平行板夹膜)为重要失效模式.对于失效情形3,需要重新进行设计计算并校核,对于失效模式2以及1-②,可采用基于TRIZ的失效解决理论进行解决,由于篇幅有限,这里不再赘述.

4　结论及展望

本文对传统FMEA中的RPN排序方法存在的问题进行了深入分析,并结合包装生产线的实际需求,提出了一种基于经济损失的风险优先值排序方法,该方法用可观的数据代替模糊的语言描述,有效解决了传统方法中不连续、重复性、灵敏度低、准确性差等问题,使得排序结果更加客观合理,更具说服性,并且操作简单,具有良好的工程实用价值.此外,之后的研究还可从以下几方面入手:1)对该方法作进一步的改进,如寻求一种更量化的计算公式使严重度的判别能够完全避免主观性干扰等;2)本文提出的ERPN方法是考虑失效模式相互独立的情况,之后可以讨论用此方法解决共因失效问题;3)不断地增加该方法的应用实例,使其对于之后的分析具有更强的指导作用,并将该方法应用到不同的生产设计中,使其更具普适性,且相应的辅助分析软件也亟待开发.

[1] LIU Hu-chen,LIU Long,LIU Nan.Risk evaluation approaches in failure mode and effects analysis:a literature review[J].Expert Systems with Applications,2013,40(2):828-838．

[2] LIU Hu-chen,FAN Xiao-jun,LI Ping,et al.Evaluating the risk of failure modes with extended MULTIMOORA method under fuzzy environment[J].Engineering Applications of Artificial Intelligence,2014,34(C):168-177.

[3] LIU Hu-chen,YOU Jian-xin,FAN Xiao-jun,et al.Failure mode and effects analysis usingDnumbers and grey relational projection method[J].Expert Systems with Applications,2014,41(10):4670-4679．

[4] LIU Hu-chen,YOU Jian-xin,YOU Xiao-yue,et al.A novel approach for failure mode and effects analysis using combination weighting and fuzzy VIKOR method[J].Applied Soft Computing Journal,2015,28:579-588．

[5] LIU Hu-chen,YOU Jian-xin,LIN Qing-lian et al.Risk assessment in system FMEA combining fuzzy weighted average with fuzzy decision making trial and evaluation laboratory[J].International Journal of Computer Integrated Manufacturing,2015,28 (7):701-714．

[6] BOWLES J B.An assessment of RPN prioritization in a failure modes effects and criticality analysis [C]//Proceedings of Annual Reliability and Maintainability Symposium.Tampa Florida:IEEE,2003:380-386．

[7] 陈政平,付桂翠,赵幼虎.改进的风险优先数(RPN)分析方法[J].北京航空航天大学学报,2011,37(11):1395-1399．

CHEN Zheng-ping,FU Gui-cui,ZHAO You-hu.The improved risk priority number (RPN) analysis method[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(11):1395-1399．

[8] 晋民杰,李辰,范英,等.基于损失费用的风险优先数分析方法研究[J].中国安全科学学报,2013,23(9):45-50．

JIN Min-jie,LI Chen,FAN Ying,et al.Research on Risk Priority Number analysis method based on loss[J].China Safety Science Journal,2013,23(9):45-50．

[9] KUTLU A C,EKMEKCIOGLU M.Fuzzy failure modes and effects analysis by using fuzzy TOPSIS-based fuzzy AHP[J].Expert Systems with Applications,2012,39(1):61-67．

[10] CHANG K H,WEN T C.A novel efficient approach for DFMEA combining 2-tuple and the OWA operator[J].Expert Systems with Applications,2010,37(3):2362-2370．

[11] GEUM Y,CHO Y,PARK Y.A systematic approach for diagnosing service failure:service-specific FMEA and grey relational analysis approach[J].Mathematical and Computer Modelling,2011,54(11):3126-3142．

[12] CHIN K S,WANG Y M,POON G K K,et al.Failure mode and effects analysis using a group-based evidential reasoning approach[J].Computers & Operations Research,2009,36(6):1768-1779．

[13] CHIN K S,WANG Y M,POON G K K,et al.Failure mode and effects analysis by data envelopment analysis[J].Decision Support Systems,2009,48(1):246-256．

[14] CARMIGNANI G.An integrated structural framework to cost-based FMECA:the priority-cost FMECA[J].Reliability Engineering and Systems Safety,2009,94(4):861-871．

[15] ZAMMORI F,GABBRIELLI R.ANP/RPN:a multi criteria evaluation of the risk priority number[J].Quality and Reliability Engineering International,2011,28(1):85-104．

Research and application of risk priority number rankingmethod based on the economic losses

GUAN Yu-ming, LIU Hui-juan, LIU Qin, WANG Xi-rui, XU Bo

(School of Mechanical Engineering, Hebei University of Technology, Tianjin 300130, China)

Aiming at the defects of conventional Risk Priority Number (RPN) methodology in Failure Mode and Effects Analysis (FMEA),such as discreteness,repeatability,low sensitivity and low accuracy,a new approach based on the economic losses named ERPN was proposed.The proposed approach consisted of two stages:qualitative analysis and quantitative analysis.The first stage aimed at determining the severity of a potential failure situation while the main task of the second stage was to calculate the probability (P) of the initial event and the economic losses (E),then took the product of the two (PandE) as the ERPN value.The new method is direct and objective and has strong maneuverability and good practicability.Besides,reverse fishbone diagram was applied to decompose the structure and the scenario theory was utilized to help analyze the failure situation.Finally,this method was used to deal with the risk priority evaluation of the failure modes of the membrane sending and packing device in the automatic packaging production line,and a satisfactory result was obtained．

failure analysis; economic loss; ERPN ranking method; reverse fishbone diagram; engineering example

2015-09-30.

关玉明(1957—),男,河北沧州人,教授,博士生导师,从事机电成套设备研究,E-mail:gyuming@163.com.http://orcid.org//0000-0002-9913-5348

10.3785/j.issn. 1006-754X.2016.03.004

TH 11

A

1006-754X(2016)03-0217-05

本刊网址·在线期刊：http://www.journals.zju.edu.cn/gcsjxb