某系统级电子装备随机振动试验方案优化技术*

杨 静，彭 超，王晓红

(中国电子科技集团公司第三十八研究所， 安徽 合肥 230088)

某系统级电子装备随机振动试验方案优化技术*

杨 静，彭 超，王晓红

(中国电子科技集团公司第三十八研究所， 安徽 合肥 230088)

随机振动试验是考察电子装备结构可靠性的关键项目。系统级电子装备集成化程度高，结构复杂，若采用传统方法制定其随机振动试验方案，则周期长且成本高。文中以某星载系统级天线模块为分析对象，提出了一种基于动态响应分析的系统级电子装备随机振动试验方案优化技术。通过建立合理的有限元模型并进行振动响应计算，能够快速获得天线模块结构各部分的振动响应，从而指导试验条件优化和响应点布置。该分析结果也可为系统级电子装备结构刚强度设计提供理论支撑。

系统级电子装备;天线模块;随机振动试验;振动响应;有限元仿真

引 言

在卫星发射过程中，电子装备往往会受到机械环境载荷的作用，机械结构作为保护和支撑电子元器件的主要载体，其结构性能需满足使用要求。随机振动试验作为考核星载电子装备环境适应性的一个主要项目，是评估产品抗振性能、耐振强度以及可靠性指标好坏的最基本的试验手段，在电子装备筛选、验收和交付试验中得到广泛应用[1]。由于航天、航空结构及其附属结构的振动问题通常以振动试验结果为最终判据[2]，因此合理制定试验方案对产品可靠性测试影响重大，其中试验条件制定和响应点布置是试验方案中需重点考虑的内容。目前，国内外均有相应的标准来规定和规范随机振动试验，如美国国防部的试验方法标准《环境工程考虑和试验室试验》和我国的《军用装备实验室环境试验方法振动试验》等[1]。

对于单机级电子装备，通常依靠规范、工程经验或试验来制定试验方案。而对于集成化程度高、结构复杂的系统级电子装备，若仍采用传统方法来确定试验条件和响应点布点位置，则成本高且周期长，并且受试验设备和测点数量的局限，试验时也不能同时获得系统级电子装备各部分的响应特性[3]。随着有限元仿

真技术在航天航空领域的广泛应用[4-6]，越来越多的设计师通过仿真方法进行结构、工艺优化设计，节约了成本，缩短了设计周期，经济效益显著。

本文以某星载系统级天线模块电子装备为研究对象，提出了基于动态响应分析的系统级电子装备试验方案优化技术，尝试将仿真技术应用于随机振动试验方案优化设计，以快速得到系统级天线模块各部分的动态响应，并且指导试验条件优化和响应点布置，达到节约成本、减小产品研制周期和提高设计效率的目的。

1 试验方案优化流程

基于动态响应分析的系统级电子装备随机振动试验方案优化流程如图1所示。首先，根据电子装备结构特征和工程特性建立合理的有限元模型，同时依据设计规范和工程经验给定初始的试验条件。然后进行随机振动仿真计算，提取响应点的振动响应，判断响应是否满足指标要求。若满足，则按初始试验条件进行试验；若不满足要求，则需要对初始试验条件进行优化，重新进行仿真计算和振动响应分析，直至振动响应满足指标要求。最后，根据仿真计算结果确定试验条件和响应点布置位置，并进行随机振动试验。

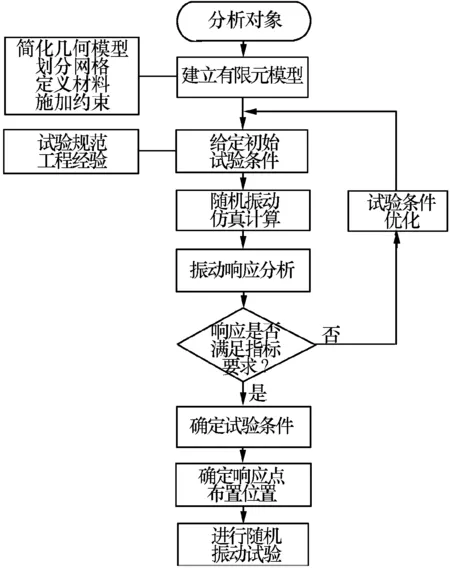
图1 随机振动试验方案优化流程

2 有限元模型

某星载雷达天线模块采用一体化结构设计，主结构为裂缝波导天线，天线上装有多个电性能单机。整个天线模块重4 kg，结构紧凑，各单机结构形式各异。综合考虑分析要求和计算机硬件要求，建立有限元模型时做了如下简化和处理：

1)对对系统振动特性影响大的天线模块主要结构进行详细建模，单机内的元器件采用质量点处理，以确保有限元模型的总质量、质量分布和质心与几何模型一致；

2)天线模块主要采用壳单元和实体单元模拟；

3)天线和单机之间的连接以及单机之间的连接均为螺钉连接，采用刚性单元模拟，单机盖板和腔体的焊接采用共节点方式处理；

4)天线模块材料包括铝合金和钛合金，临界阻尼比取为0.03。

图2为通过Hypermesh软件建立的有限元模型。

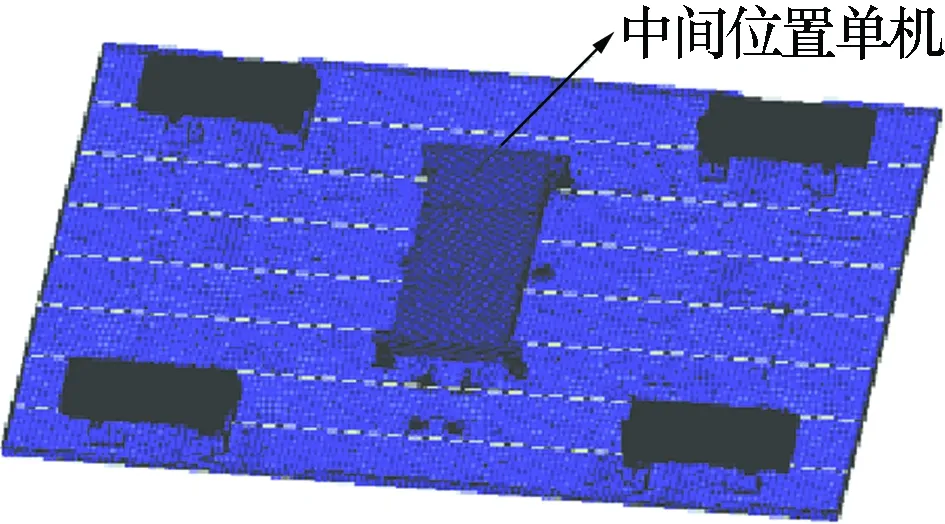
图2 天线模块有限元模型

3 初始试验条件设定

表1为根据指标要求确定的天线模块上各单机的试验条件。由于系统级天线模块试验条件难以确定，因此暂将单机试验条件设定为天线模块的初始试验条件。

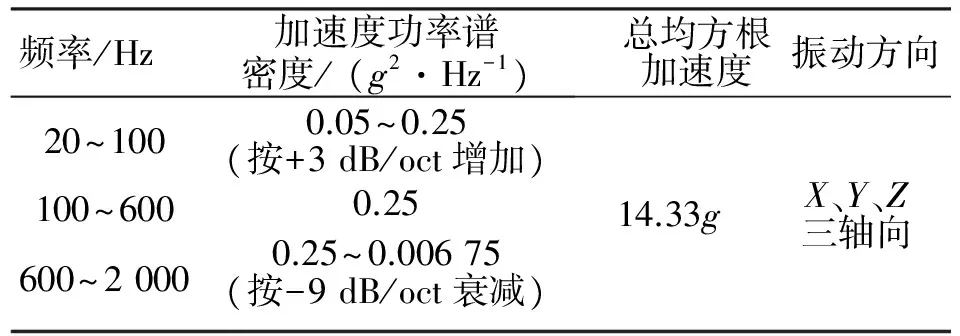
表1 随机振动分析输入条件

4 随机振动仿真分析

本文采用模态叠加法进行X、Y、Z方向随机振动分析。模态分析是进行随机振动分析的基础，仿真时提取了2 000 Hz以内的所有模态，计算得到天线模块的基频为400 Hz，满足结构设计对刚度的要求(基频大于100 Hz)。

随机振动分析发现，天线模块上加速度响应的最大区域位于中间位置单机处，图3为提取的加速度响应分布云图。X、Y、Z方向随机振动时中间位置单机安装位置的均方根加速度值分别为25.9g、32.9g和79.5g，较初始试验条件(见表1)分别放大了1.8倍、2.3倍和5.5倍。

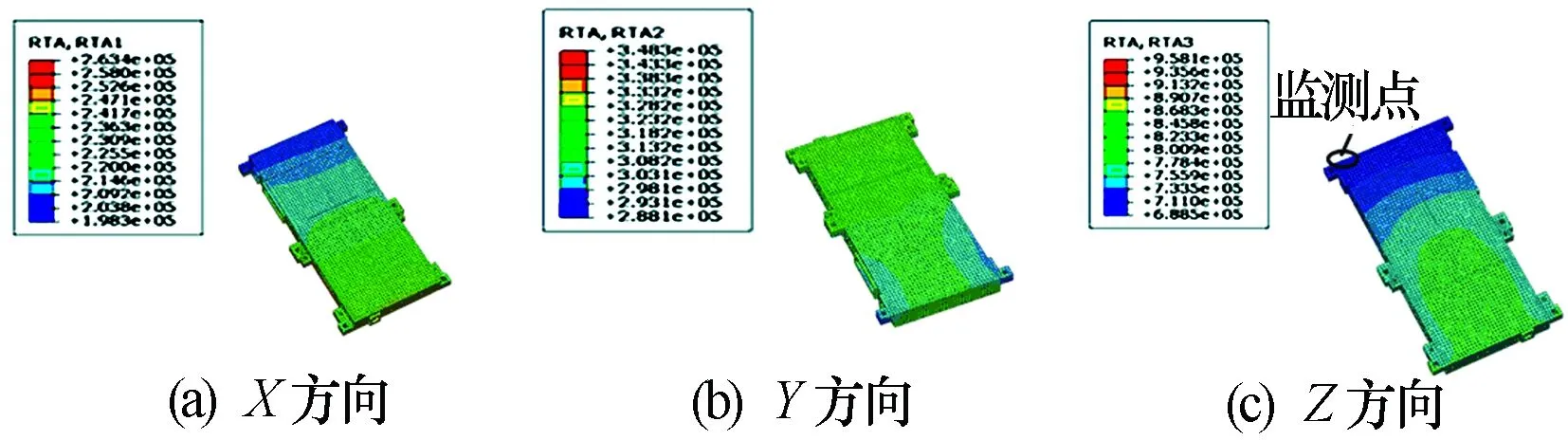
图3 X、Y、Z三个方向的振动响应

综合X、Y、Z方向随机振动时的应力计算结果，Z方向随机振动时天线模块的应力最大，如图4所示。取安全系数1.5，按最大米塞斯应力3σ进行强度校核。天线模块上除天线外的其他单机结构强度安全裕度均大于0，满足设计要求；而铝合金材料天线的1σ应力最大值为30 MPa，该材料屈服强度为115 MPa，天线强度安全裕度小于0，不满足强度设计要求。

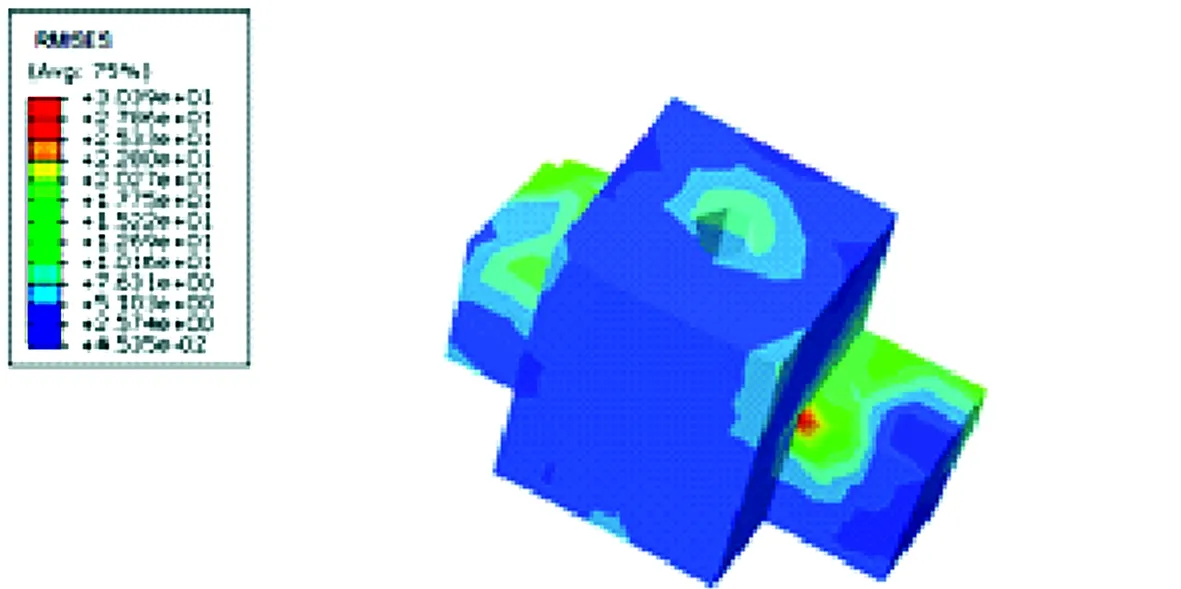
图4 Z方向随机振动时天线应力分布

5 试验方案优化

5.1 优化依据和优化方法

仿真计算表明，天线模块基频满足刚度要求，而天线强度和模块上单机振动响应均不满足指标要求。随后，按单机试验条件进行天线模块随机振动试验，发现单机结构振动响应放大倍数与仿真分析结果相近，说明仿真分析过程合理可信。

由于受结构总体给定重量指标要求的限制，天线模块重量增加空间有限，因此通过增重来提高天线刚度的办法不可行。因此，从确保单机不产生过试验的角度考虑，将天线模块试验条件由单机试验条件优化为限幅控制，以保证天线模块上单机安装位置的最大振动响应满足单机指标要求。

5.2 控制点和响应点选择

控制点是电动振动试验系统中作为闭环控制输入的加速度计在振动台台面、夹具或被测设备上的具体位置。根据控制点的选取原则，将夹具上靠近与天线模块的连接点处作为控制点的布点位置。

由于仿真分析得出天线模块上中间位置单机处加速度响应较大，因此测试时将响应点布置在中间位置单机响应较大的安装位置附近，如图3(c)所示。

6 随机振动试验

对天线模块分别进行X、Y、Z方向的随机振动试验，试验夹具选用铝合金材料，经分析，夹具结构基频大于2 000 Hz，满足试验要求。试验结果表明：响应点的均方根加速度响应值控制在14.33g以内，完全满足单机的指标要求，且天线模块振后结构完好，未发生强度破坏，经测试电讯指标也满足要求，如图5所示。

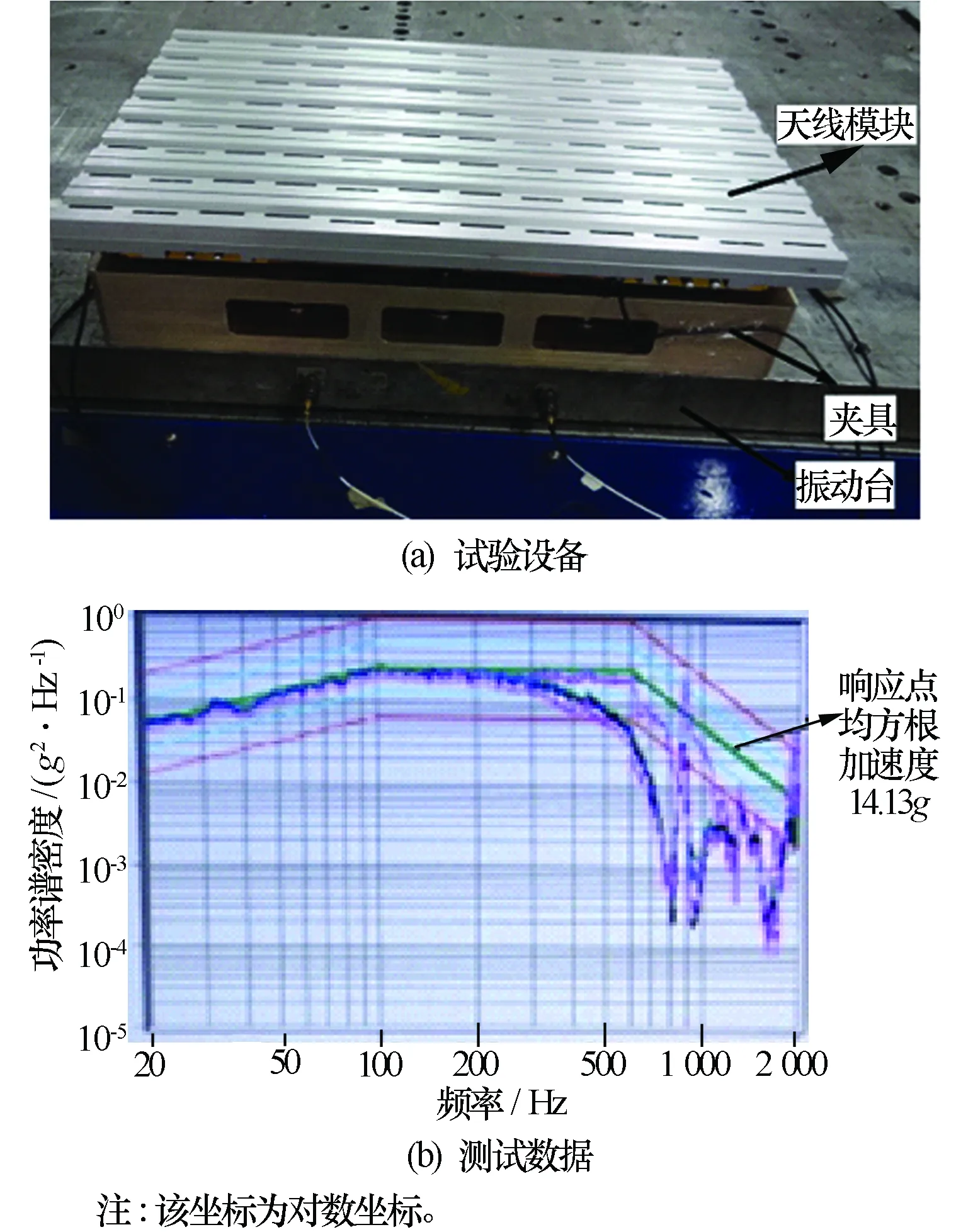
图5 随机振动试验

7 结束语

本文提出了一种基于动态响应分析的系统级电子装备随机振动试验方案优化技术，可快速且同时获得系统级电子装备各个结构部位的动态响应，在指导试验条件优化和响应点布置的同时，还可为结构刚强度设计提供理论依据。相对于传统依靠设计规范、工程经验和试验法优化试验方案的模式，该方法可降低产品的研制成本，缩短研制周期。它已成功应用在某星载系统级天线模块随机振动试验条件的制定中。

[1] 马红卫. 随机振动试验中确定控制点布置方案的方法[J]. 可靠性与环境试验技术及评价, 2015, 33(3): 26-30.

[2] 姜节胜, 高跃飞, 顾松年. 环境振动试验技术的若干新进展[J]. 机械强度, 2005, 27(3): 307-311.

[3] 邱吉宝, 王建民. 航天器虚拟动态试验技术研究及展望[J]. 航天器环境工程, 2007, 24(1): 1-14.

[4] 管宇辉. 某星载设备环境综合仿真[J]. 机械研究与应用, 2013, 26(6): 88-95.

[5] 吴孟武, 黄春江. 某星载设备环境综合仿真[J]. 机械研究与应用, 2013, 26(6): 88-95.

[6] 王尚礼. 某航空机箱动力学性能仿真技术研究[D]. 西安：西安电子科技大学, 2012.

杨 静(1982-)，女，博士，高级工程师，主要从事结构力学仿真、测试研究工作。

Optimization Technology for Random Vibration Test Scheme ofSystem-level Electronic Equipment

YANG Jing，PENG Chao，WANG Xiao-hong

(The38thResearchInstituteofCETC,Hefei230088,China)

The random vibration test is the key to the structure reliability test of the electronic equipment. Because of high integration and complicated structure of the system-level electronic equipment, the traditional random vibration test works with long cycle and high cost. Based on dynamic response analysis, the random vibration test scheme optimization technology of the system-level electronic equipment is proposed for a space-borne system-level antenna module. The structure vibration response of the antenna module can be obtained quickly by setting up a reasonable FEM model and carrying out vibration response computation. The results can provide guidance for the test conditions optimization and the response point arrangement and supply theoretical basis for the structure stiffness & strength design of the system-level electronic equipment.

system-level electronic equipment; antenna module; random vibration test; vibration response; FEM simulation

2015-12-03

TP391.9

A

1008-5300(2016)03-0005-03