RBFN优化算法在键合机标定中的应用
洪 喜,李 维,卢 佳,白 虹,孙海波
(中国科学院长春光华微电子设备工程中心有限公司,长春130000)
RBFN优化算法在键合机标定中的应用
洪喜,李维,卢佳,白虹,孙海波
(中国科学院长春光华微电子设备工程中心有限公司,长春130000)
键合位置精度是衡量键合机性能的关键指标之一。为提高键合工具的键合位置精度,针对键合位置误差的非线性特点,提出一种径向基神经网络误差修正方法。以键合角度与键合点图像坐标为学习样本,以生成最小映射误差为原则调节网络权因子、基函数中心和宽度,建立具有良好泛化能力的误差逼近模型。并根据算法特点提出了一种工程优化方法,在保证算法补偿精度的基础上使得其运算时间也满足工作需要。实际工作表明:采用此种方法可将键合精度提高一个数量级,有效地改善键合位置精度并且很好地解决非线性误差对系统的影响。
径向基函数网络;键合机;误差;修正;精度
1 引言
引线键合技术是目前半导体封装制造的主流技术。它是一种由键合工具引导金属引线使框架基底和芯片上的焊点连接起来的过程。键合工具作为直接作用于键合金属表面[1]的执行部件,是超声波键合机的关键组件之一,它的定位精度直接影响键合机的整体性能指标与键合精度。键合工具的安装对焊接质量的影响已有论述[2~4],但是在相关论述中关于键合位置的系统标定与修正方法并未见到。
在国内常见的超声波铝丝键合机中,焊头虽可进行±100°以内的旋转,但是旋转角度或是预先设定,或是限定在较小的范围内,此种情况往往并不需要对键合工具的键合位置进行复杂的标定与修正。但是旋转角度的限制使得此种键合机对于焊区的适应情况非常单一。而随着市场上对降低成本、提高效率的需求,目前已经出现芯片倒置粘贴,或多排引线框架集成框架整体的制造与加工形式,这就使得焊头可大角度(超过180°)旋转、键合角度灵活可控的键合机成为应用趋势。它的工作方式灵活可靠,适应性更广。
在键合机中,键合工具直接作用于焊接表面,它是键合动作的最终执行部件。键合工具理想的安装位置本应与焊头轴心重合或与轴心保持相对固定的位置关系,以使焊头旋转运动时键合工具的运动轨迹可保持恒定。原有的键合原点标定[5]采用如下方法:键合工具在物体表面上打一点(x0,y0),然后通过图像系统看到的实际点与键合头十字坐标不一致,把键合头上十字坐标移动到所打的实际点上,这时的坐标为(x1,y1),校正的补偿值即为:Δx=x1-x0,Δy=y1-y0。对于焊头旋转角度小(某些键合设备采用键合平台旋转固定角度的方式以补偿键合位置偏差)、键合区域相对单一的芯片,这种方法操作简单,补偿精度满足键合需要。但是随着芯片种类的增加与粘片方式的多样化,焊头往往需要实现大角度旋转,同时在键合过程中,焊头需要根据用户需求或者芯片焊区和框架引脚的位置关系实时改变其旋转角度。另外,键合工具的安装位置也受加工工艺与安装精度的影响,更换焊头或对同一焊头采用不同的安装方法都会造成相互位置的变化,这样就更难以确定键合工具与焊头轴心的相对位置。此时若仍采用键合原点标定法进行键合点位置补偿,已经无法满足焊头在各个旋转角度下的补偿需要,甚至会带来更大的位置偏差。而键合工具作为焊接动作的执行部件,它的定位不准确不仅会造成大量不合格芯片产品的产生甚至会造成工具与变幅杆等关键部件的损坏。如何进行键合工具的键合位置标定或修正成为键合机必须解决的问题之一。
2 RBFN修正方法
2.1方法的提出
旋转焊头并在引线框架上标记出键合位置,如图1所示。由图1可见,键合工具的键合轨迹是一条曲线。当焊头旋转角度较小时,该曲线类似一个圆弧,笔者已另有文章对此做过论述。而当旋转角度较大甚至超过180°时,键合轨迹逐渐趋于一条无规则曲线。由于影响键合轨迹的成因复杂,难以用简单的数学模型进行描述,因此具有良好的自学习、自适应和非线性动态处理特性,可以高精度地逼近非线性曲线的RBFN网络成为解决问题的较好选择。
2.2RBFN的工作原理
RBFN模型[6~7]如图2所示。

图1 键合轨迹示意图
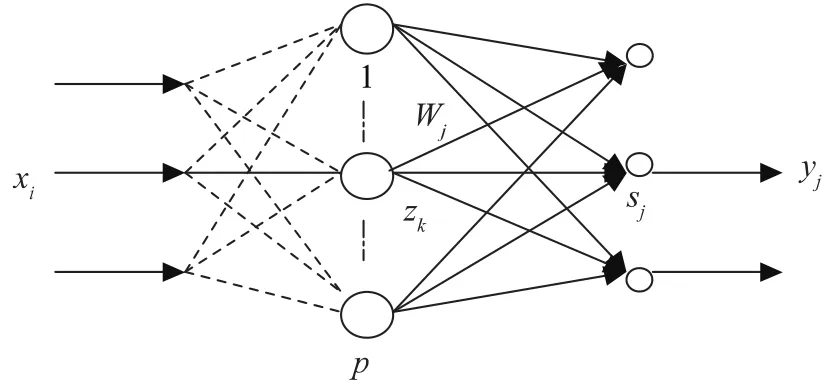
图2 RBFN模型
RBFN算法的数学模型如式(1)与(2):

其中,x为输入模式;Ck为径向基函数中心;Φ()为隐层完成非线性转换的非线性函数,通常采用高斯函数,即:;zk为网络隐层的输出。
wjk是输出结点j到隐层的第k个结点的权向量;f()是输出层的线性函数,yj为网络实际输出。
2.3RBFN的键合位置修正
RBFN用于键合位置修正的建模原理可以简述如下:建立单隐层前馈RBFN;在图像坐标系下,设焊头旋转i°时的键合点坐标为(pxi,pyi)。将离散的旋转角度进行归一化处理后作为网络输入,将同一角度位置的键合点图像坐标作为网络输出,不断调整网络参数,直到建立的网络可以较好地拟合出整条键合轨迹曲线。
由RBFN模型可知,权值与中心的调整是决定网络性能的关键。文中采用正则化的正交最小二乘法进行网络训练,所建模型具有精简的网络结构、良好的建模精度与优秀的泛化能力。
3 RBFN的工程优化
由于RBFN算法涉及到大量的矩阵运算与幂指数运算,若采用原始算法,当隐层结点数过多时,运算时间可能达到ms级,在对运算时间要求严格的情况下就要对算法进行优化。
由RBFN的工作原理可知,隐层设计的目的是反映隐层结点偏离输入模式的程度。当输入模式恰好位于隐结点中心Ck时,

输入x偏离Ck时,随着偏离程度的增加,隐层输出zk减小。也即对于输入模式而言,只有进入隐结点的覆盖范围才会产生输出。因此可设一数值Temp,只有:
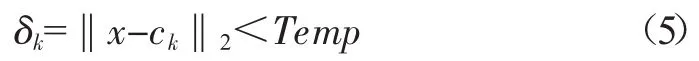
才有必需计算隐层输出zk,其余则可直接令zk=0。
对于满足公式(5)的隐结点输入,继续做高斯运算时仍需耗费大量运算时间,因此对其进一步化简。首先将径向基函数用泰勒级数展开,即:

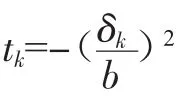
式中,,它反映了编码器采样点偏离径基中心的程度。但公式(6)中‖tk‖>1时,m需要取值极大才能使公式收敛,与优化原则不符,对其处理如下:

tkint为幂指数的整数部分,此部分的运算结果可通过查表方式得到。小数部分的运算则按泰勒展开式进行。
4 实验分析
4.1RBFN的建模
以全自动超声波铝丝键合机DAB-1027为例,选择TO-220框架及可控硅芯片作为实验对象。首先在空白的引线框架上分别标记出焊头旋转-135°,-105°……135°时的键合位置,对输入角度数据进行归一化处理并将其作为训练样本。以公式(8)所示的标准偏差作为误差曲线拟合效果的度量。

其中xi、yi是第i次键合位置图像坐标,x、y是键合的期望值,也即设定的键合准确位置。
补偿前的系统误差如图3所示。
补偿后的系统误差曲线如图4所示。
选择4个焊头分别进行上述实验,并将RBFN方法与原点标定法以及圆拟合法的补偿结果进行比较,见表1。

图3 补偿前系统误差曲线
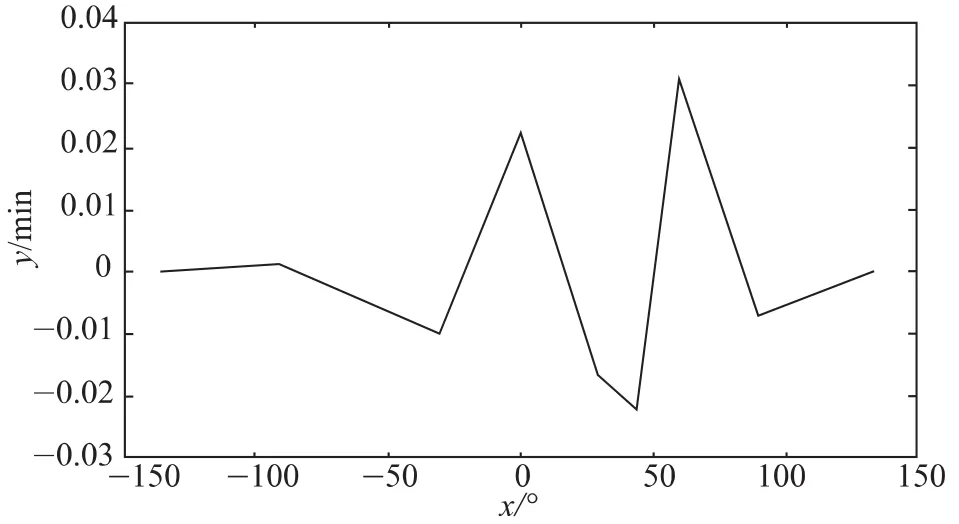
图4 补偿后系统误差曲线

表1 修正结果对比
由表1可见,经过RBFN补偿后,系统精度明显改善。
4.2键合实验
首先在芯片上手动标记出键合位置,如图5中的十字标记所示;然后根据RBFN模型计算出键合点图像坐标;将图像坐标系转换为运动坐标系,控制焊头精确定位到设定位置,完成键合动作。
未进行RBFN修正时,键合位置如图5中箭头所示。对键合位置进行修正并重新键合,键合效果如图5。

图5 键合结果对比
5 结论
(1)采用RBF误差修正后,可将键合精度由0.8mm提高到0.04 mm以上,显著提高了系统精度;
(2)RBFN误差补偿法可以视为对检测基准逼近的一种统计性计算方法,因此样本点的选择与数量将影响补偿精度;
(3)RBFN方法无需对误差成因及分布做复杂的分析测试工作,可在众多领域推广应用。
[1]ZHONG Z W,GOH K S.Investigation of ultrasonic vibrations of wire bonding capillaries[J].Microelectronics Journal,2006,37(2):107-113.
[2]K S Goh,Z W Zhong.Development of capillaries for wire bonding of low-k ultra-fine-pitch devices[J].Microelectronics Engineering,2006,23(4).
[3]姚钢,韩雷.劈刀安装长度对引线键合强度影响的实验研究[J].压电与声光,2008,30(4):414-416.
[4]冯武卫,范虹,孟庆丰,董光能.引线键合系统键合工具振动特性研究[J].振动与冲击,2007,26(7):106-110.
[5]易辉,刘晓斌,宫晨.全自动引线键合机校正系统设计与实现[J].电子工业专用设备,2005,131:30-33.
[6]Chen S,Chng E S.Regularized orthogonal least squares algorithm for constructing radial basis function networks[J]. International Journal of Control(S0020-7179),1996,64(5):829-837.
[7]李鸣鸣,龚振邦.长光栅误差的神经网络建模分析[J].机械与电子,2004,6:59-61.
Error Compensation Based on RBF in Bonder
HONG Xi,LI Wei,LU Jia,BAI Hong,SUN Haibo
(Changchun Guanghua micro-electronics equipment Engineering center Co.,Ltd.,Changchun 130000,China)
To improve precision of bonding position which is a key technical index for bonder,a new compensation method based on neural network was proposed.A model based on Radial Basis Function(RBF)was set up,in which the output was bonding coordinate and the input was bonding angle.According to the inhibit condition between the test value and the output of the network,adjusting power factor formula and the center and width of the radial basis function to make the model have a good learning ability and generalization ability.The optimization algorithm reduces the running time to a practical degree but doesn't decrease the compensation precision obviously.The test results show that the system precision is improved by an order of magnitude by this optimal method and the nonlinear effect on the system is reduced.
radial basis function network;wire bonder;error;compensation;precision

TN762,TP183
A
1681-1070(2016)05-0007-03
2016-2-26
洪喜(1980—),女,吉林省长春市人,博士研究生,副高级工程师,主要从事计算机技术、光电传感器技术的研究。

