基于气象因子的碧螺春茶年产量预测模型

王明月，徐常青，韩 敏，李 贤

（苏州科技大学 数理学院，江苏 苏州215009）

基于气象因子的碧螺春茶年产量预测模型

王明月，徐常青*，韩 敏，李 贤

（苏州科技大学 数理学院，江苏 苏州215009）

研究苏州洞庭碧螺春茶产量与气象因子之间的关系。通过对2008年至2013年气象因子及碧螺春产量数据的处理，并将每月分为上、中、下旬，产生20个因子，生成一个6×20的数据矩阵。通过对该矩阵的偏相关性分析和逐步回归分析，发现2月中旬日平均日照时数、2月下旬日平均最高温和3月上旬日平均最低气温这3个因子对茶产量影响较大，由此建立它们与碧螺春茶产量之间关系的回归模型。该模型可用于对碧螺春茶产量进行预测。

碧螺春；气象因子；逐步回归；预测模型

洞庭东山，又称东山，位于苏州市西南部，是太湖中的一个半岛。东西山碧螺春茶已有千年历史［1］。 碧螺春茶的特点即“一嫩三鲜”：芽叶嫩，且色、香、味鲜，鲜叶碧绿，炒制而成的成品茶形似螺旋，满披茸毛，所泡茶水清澄，香气扑鼻，因其色、香、形兼备而得名为“碧螺春”。碧螺春为绿茶之首，是中国十大名茶之一。

早春的太湖升起的浓浓雾气使得嵌入其中的东山空气湿润，土壤呈酸性且质地疏松。这种环境宜于茶叶生长。茶果间植的生态环境又孕育了碧螺春独特的花香气息［2］。但碧螺春茶每年长势因气候而变，产量也有所不同。在气温稳定在10℃以上时，碧螺春茶的茶芽、叶片生长加快，并抽出新梢；15-20℃时叶片生长较快，20-30℃时生长最旺盛。在茶叶采摘过程中，新梢不断萌发，茶叶相继采摘，这段时间茶树需要连续补充水分和光照，因而一般要求年降雨量1 500 mm左右、月降雨量100 mm以上。由于苏州典型的江南气候，春季低温阴雨（且多连绵细雨），盛夏高温少雨、干旱都会影响茶叶的产量［3］。一般而言，碧螺春茶主要是指早茶，每年春分前后开采，谷雨前后采摘结束。碧螺春茶在苏州地区全年茶叶生产中，经济效益比例最大［4］。随着我国总体经济和苏州经济的发展，人们对茶叶的需求在增加，因此，碧螺春茶近几年的产量也得到了快速提升。如2013年，苏州吴中区茶园面积共2 056 hm2，茶叶总产量315 t，其中碧螺春产量150 t，占总产量47.6%，茶叶总产值2.38亿元，其中碧螺春产值1.67亿元，占总产值70.1%。

通过2008年至2013年近6年碧螺春茶产量数据，可看出碧螺春茶年产量存在明显波动。显然，茶树品种、气候变化、施肥方案、栽培技术等都是影响碧螺春茶产量的重要因素。这其中，研究者发现与碧螺春茶产量最密切相关的因素当属气候变化［5］。笔者希望通过数据分析的手段，对气象因子进行合理选取，掌握采摘时段气象因子与产量间的简单而又合理的依存关系，来对茶叶生长期进行科学合理的人工干预，从而达到增加碧螺春茶产量和经济效益的目的。

笔者在以前工作的基础上，进一步研究东山碧螺春与当地气象因子的关系。选取东山早茶碧螺春中槎湾1号品种（下称碧螺春）为研究目标，记茶树的一芽一叶期始至一芽两叶期始为碧螺春的采摘期。通过对2008年至2013年碧螺春产量与采摘期的各个气象因子的相关性分析，结合逐步回归分析和MATLAB （R2009a）工具，将变量一个个引入到模型中，若其偏回归平方和经验显著则变量保留，反之剔除该变量，最后得出对碧螺春茶产量影响较大的气象因子，建立产量与气象因素的预测模型［6-8］。

1 材料和方法

1.1 资料来源

茶树生育期及碧螺春产量的相关数据来源于东山镇农林服务中心，主要有2008年至2013年的茶叶总产量和碧螺春的产量；气象资料来源于苏州吴中区东山气象站，主要包括2008年至2013年2月份至4月份的气象数据。表1显示的为部分气象数据。

表1 2008年至2013年的部分气象数据

1.2 数据处理和分析方法

1.2.1 数据处理

文中选取碧螺春生长期的原始气象数据为近6年2月1日至4月30日的日平均气温、日最低温、日最高温、日降水量及日照时数。产量数据是2008年至2013年槎湾1号每年的鲜叶产量。考虑到若以天为单位（即以每天的数据为一个采样点），则样本点过多；若以年或月为单位，则样本点过少，且由于茶叶生长一般集中于2月中旬至4月下旬，故以月为单位不合适。为此，文中以旬为单位（注意到2月下旬天数不一），求得各因子的旬日平均值（见表2）。

表2 2008年至2013年部分的气象数据

笔者将这些因子按旬为时间单位进行细化，细化后得到20个因子，见表3。

表3 细化后的因子矩阵

表3产生5×4的因子矩阵M，其中元素xij表示第j个因子在时间节段（旬）i处对应的细化因子。利用MATLAB（2009a）矩阵向量化指令M（：）将因子矩阵M转化为一个列向量p，则p为一个20维的列向量，再将向量p转置得行向量x，向量x在每年的采样数据为一个维数为20的样本点。文中选取2008，2009，…，2013年对应的6个样本点S1，S2，…，S6。依次以该6个样本点为行向量生成数据矩阵A

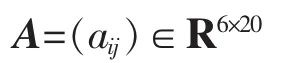
A为一个6×20的矩阵。对矩阵A进行标准化处理

以克服不同气象因子量纲之间的差异，便于进行变量之间的比较。（1）式中，Xij表示矩阵A的第i行第j列的元素标准化后的数据，aij为旬日平均因子值，为原始序列平均值，（n为样本个数）为原始气象因子序列值的均方差。以上处理过程可用下述步骤说明：

Step1 生成因子矩阵

Step2 将矩阵M向量化，对应MATLAB指令为p=M（：）；x=p′。记x=｛a1，a2，a3，…，a19，a20｝。

Step3 根据6个样本点写出数据矩阵

其中A的第i行Si表示第i个样本点，A的第j列表示第j个变量。

Step4 将矩阵A标准化，对应MATLAB指令为＞＞X=zscore（A）。该指令输出变量X为大小6×20的矩阵，其第j列为第j个变量标准化后的数据序列。

1.2.2 分析方法

文中通过采用逐步回归分析法，选取对碧螺春产量影响最显著的3个气象因子。逐步回归法是在回归模型的所有自变量中按其对因变量的作用、显著程度（贡献）的大小逐个引入回归方程中。这里要求引入的变量的F统计量在某个给定水平上为显著的。逐步回归法从回归方程中剔除那些非显著性变量，然后按偏回归平方和由小到大地依次对方程中其余变量进行F检验。检验后，再考虑是否引入新的变量。当模型外的所有变量在给定水平上均非显著，且模型中变量的F统计量在给定水平上为显著时，逐步回归法过程停止［9-12］。

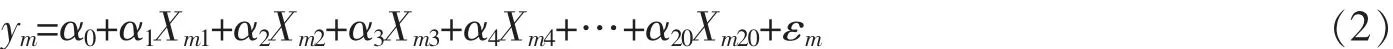
设变量y表示碧螺春茶叶每年的产量，则y满足带噪声回归模型其中噪声项εm独立同分布服从N（0，δ2）。（2）式可等价改写为其中α＝（α0，α1，α2，…，α19，α20）T为一个21维列向量，T＝（X1，X2，…，X20）T为一个6×20的矩阵，ε＝（ε1，ε2，…，ε6）T。并且E（ε）＝0，D（ε）＝δ2I6×6。

由于（2）式中有21个未知参数，解出这些未知参数至少需21个方程，故文中的6个数据点无法求解所需的参数。为此，需挑选出至多5个对碧螺春茶产量影响最显著的气象因子。

文中第二部分将以茶树生长发育期间的气象因子作为影响碧螺春产量的待选预测因子，利用MATLAB （R2009a）软件对数据进行逐步回归分析，来建立碧螺春产量的预测模型。

2 预测因子的选取及分析

2.1 主导气象因子的确立

经验所知，茶叶生长发育的关键时间应为2月中旬至3月中旬，且主导碧螺春生长的因子为日最低气温和日平均降水量，研究者运用偏相关分析法从20个因子中选取若干主导气象因子［13］。

＞＞for j＝1∶20

＞＞Nj=corrcoef（X（：，j），Y）

＞＞end

由MATLAB（R2009a），计算得出碧螺春产量与气象因子间的偏相关系数（见表4）。再为保证引入方程的预测因子数目，根据指令＞＞stepwise（X，Y，0.025，0.075），将通过显著水平0.025的因子引入方程，将小于0.075的因子剔除。

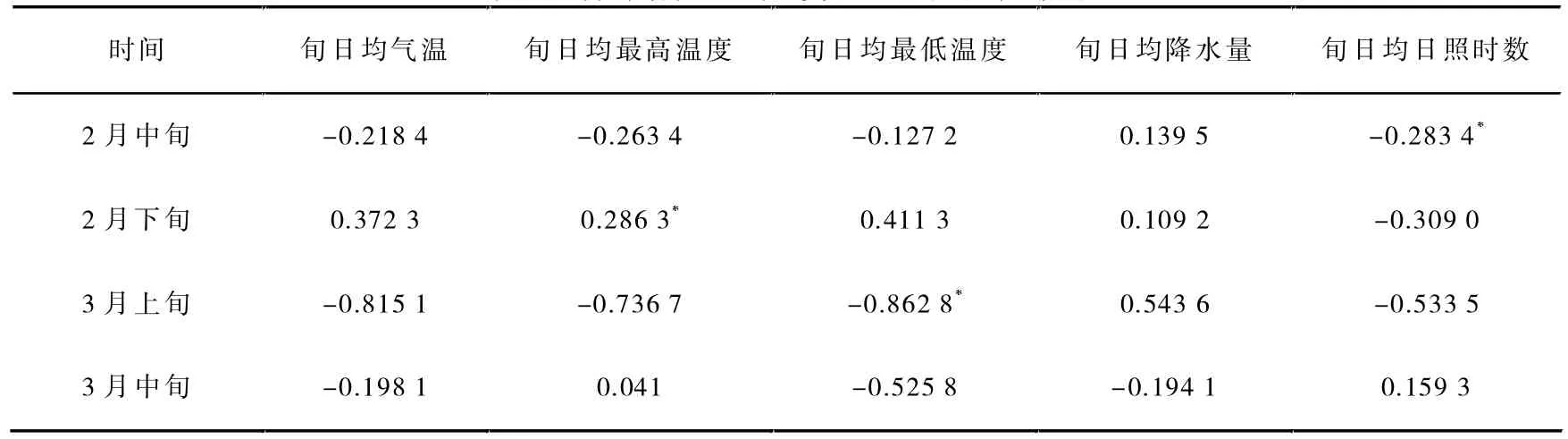
表4 碧螺春产量与气象因子间的偏相关性

表4给出的是各气象因子与碧螺春茶产量之间的单相关关系，其中2月中旬的日平均日照时数、2月下旬的日平均最高温和3月上旬的日平均最低温与碧螺春茶产量之间的相关性通过0.025水平的显著检验。

2.2 预测因子分析

由表4知，2月中旬的日平均日照时数和3月上旬的日平均最低温度与碧螺春产量呈负相关，2月下旬的日平均最高温度与碧螺春产量呈正相关。在茶叶生长发育中，2月中下旬至3月上旬为茶叶萌动期，此时的气温对茶芽的萌发影响较大，当平均气温达到7.5℃时，有利于休眠状态的越冬芽逐渐膨大，即有利于茶芽萌动。在笔者收集的2008年至2013年的数据里，2月中旬的旬日均日照时数分别为7.110 0，2.420 0，5.750 0，3.800 0，3.400 0，3.770 0 h，说明2月中旬多阴雨天气，不利于茶芽萌发生长［3］；2月下旬的旬日平均最高温分别是12.155 6，8.150 0，16.162 5，13.325 0，7.366 7，12.575 0℃，除2012年外都高于7.5℃，且2012 年2月下旬的旬日平均最高温（7.366 7℃）接近7.5℃。因此，采集到的6个样本点的2月下旬旬日平均气温有助于茶芽萌发；3月上旬的旬日平均最低温分别为5.290 0，4.570 0，2.390 0，3.450 0，4.590 0，7.050 0℃，都低于7.5℃，其中2010年3月上旬旬日平均最低气温最低。在其他因子数值确定的前提下，该样本点对应的碧螺春产量应为最低。但实际情况恰恰相反：2010年碧螺春茶产量2 754 kg·hm-2，为6年中最高，说明该回归模型为多变量回归模型。事实上，由以上数据分析可看出，它同样非双变量回归模型。

综上所述，选取的预测因子基本与事实相符。

2.3 逐步回归预测模型的建立

根据MATLAB（2009a）代码＞＞M=corrcoef（X）得出20个气象因子间的相关性矩阵M，由M中元素知这20个气象因子之间有较强相关性，在矩阵M中选出预测气象因子间的相关性系数（表5）。

表5 预测因子间的相关性系数

可见预测因子间的相关性系数的绝对值都小于0.6，不具有较强的相关性。

用MATLAB（2009a）做多元线性回归，程序为：

＞＞XX=［ones（6，1）X5'X7'X13'］

＞＞α=inv（XX'*XX）*XX'*Y

根据结果建立逐步回归模型

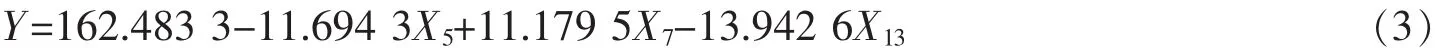
其中：X5为2月中旬日平均日照时数，X7为2月下旬日平均最高温，X13为3月上旬日平均最低温度。

注意到回归方程 （3）中三个因子变量（X5，X7，X13）中的其中两个因子变量（X5，X13）前面的系数为负数，这表明因子X5和X13对碧螺春茶产量起抑制作用，即2月中旬日均日照时数的过长以及3月上旬日均最低温度的过高都会对碧螺春茶有不利影响，而2月下旬日均气温（即X7）促进碧螺春茶产量的增长，这与实际情况完全吻合。事实上，温度与产量呈现负相关性这种现象在植物生长模型方面并不少见［14］。

3 回归模型的显著性检验与讨论

3.1 相关系数检验

根据MATLAB（R2009a）［15］剔除部分自变量后得到多元回归模型（3），其中复相关系数R2=0.990 1，即R= 0.995 0，调整后的R2=0.975 2，即R=0.987 5，查相关系数表得R3，2，0.025=0.950 0，R＞R3，2，0.025，故因变量与自变量相关性较好。伴随概率p=0.014 8，统计量F=66.614 6，剩余标准差为RMSE=2.894 5，查表可得

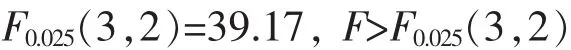
故所建回归模型显著性较好，具有实际意义。

3.2 预测模型的检验

利用建立的模型（3），结合2008年至2013年的气象数据，计算出历年的预测值。具体实际产量与预测产量的差异见表6。

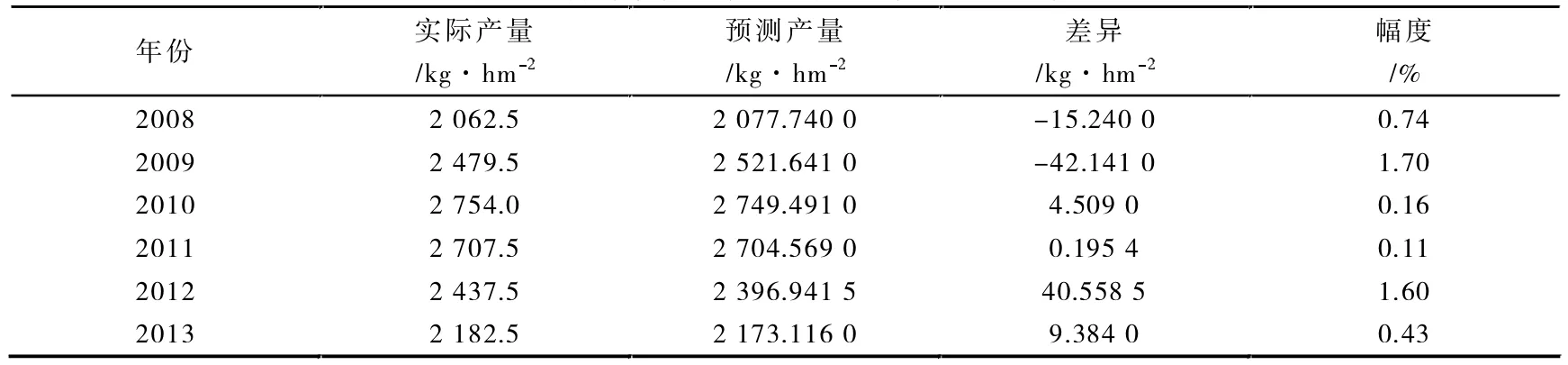
表6 碧螺春实际产量与预测产量比较情况

运用模型对2008年至2013年茶产量及其气象数据的分析检验，发现由模型（3）计算得出的预测值与实际值差异均低于2%，基本上相符。说明建立的气象因子与碧螺春茶产量的回归模型预测精度较高，可以用于碧螺春茶的产量预测。

可以根据回归方程（3）中碧螺春茶与各气象因子的正负相关性，在碧螺春茶萌动、萌发时，对茶树生长环境的温度、降水、日照时数加以调节，防止温度过高、降水较少、日照时数较多等。例如：碧螺春茶树一般种植在果树花丛中，可以考虑间作的植物之间的高低问题，这样有利于茶树与外界的温度交替，也有利于降水与日照时数的控制。

4 结语

文中通过选取碧螺春茶芽萌动、萌发及生长各时段的各个气象因子，并根据逐步回归分析建立了关于碧螺春产量与气象因子之间的回归模型。通过检验，所建立的模型预测精度较高，可以作为槎湾1号产量预测，并得出在茶叶生长的各个时段气象因子对碧螺春茶产量影响的程度。文中的预测模型只针对碧螺春的槎湾1号品种，对于其他品种的茶树则需要另外考虑。另外，由于建立模型只考虑部分影响碧螺春产量的因素影响，对虫害影响、土壤、施肥情况等因素未予考虑，所以预测值会有一定的偏差，这也有待于进一步的探索。

［1］袁卫明，陈易飞，李庆奎，等.苏州洞庭山碧螺春发展的现状与对策［J］.茶叶通讯，2011，38（3）：42-44.

［2］张旭辉，王俊，蒯志敏.苏州近51年茶园早春湿润指数变化特征及其影响因素［J］.江苏农业科学，2013，41（3）：342-345.

［3］程佳，王俊，蒯志敏.洞庭山碧螺春茶叶生产适应性气候分析及高产对策［J］.现代农业科技，2010（6）：305-306.

［4］沈永源.吴县洞庭山区茶叶生产劳动管理调查［J］.茶叶科学，1965（4）：63-65.

［5］张利华，张永强，张仁祖，等.用气象因子预测徐州地区棉花产量的研究［J］.江西农业学报，2010，22（8）：108-110.

［6］李焕，李春芳，何峥嵘，等.哈巴县打瓜产量与气象因子的关系及产量［J］.安徽农业科学，2011，39（19）：11752-11753，11789.

［7］廖爽，叶枫，武英.基于MATLAB的逐步回归法计算新疆伊犁地区煤的发热量［J］.煤质技术，2011（4）：1-5.

［8］韩敏，徐常青，王明月，等.碧螺春茶产量与采摘期气象因子的关系［J］.苏州科技学院学报（自然科学版），2015，32（2）：6-9.

［9］汪洁瑾，袁姗姗，黄萃琳.房产需求量中的若干数学模型和研究［J］.应用数学与计算数学报，2008，22（12）：49-56.

［10］刘晓宇，孟军.基于逐步回归的黑龙江省烟叶产量预测［J］.中国农学通报，2012，28（7）：223-227.

［11］贺建宁，李俊雅，许尚忠，等.应用逐步回归法估计中国西门塔尔牛体重的研究［J］.中国畜牧兽医，2009，36（9）：199-201.

［12］RAHIMI-AJDADI F，ABBASPOUR-GILANDEH Y.Artificial neural network and stepwise multiple range regression methods for prediction tractor fuel consumption［J］.Measurement，2011，44：2104-2111.

［13］石娟，李镇宇，闫国增，等.林分因子与舞毒蛾危害程度的风险评估［J］.林业科学，2004，40（1）：106-109.

［14］季彪俊.影响水稻产量因子研究［J］.西南农业大学学报（自然科学版），2005，27（5）：579-583.

［15］胡良剑，孙晓君.MATLAB数学实验［M］.北京：高等教育出版社，2006：50-53.

责任编辑：谢金春

The annual output forecast model of Biluochun tea based on meteorological factor analysis

WANG Mingyue，XU Changqing，HAN Min，LI Xian
（School of Mathematics and Physics，SUST，Suzhou 215009，China）

In the paper，we studied the relationship between the output of Biluochun tea and the meteorological factors by using climate data in the growing period of Biluochun tea.Based on the data from 2008 to 2013，we obtained 20 factors and formed a 6×20 matrix.Through the correlation analysis and stepwise regression analysis of the matrix，we established the relationship regression model between meteorological factors and Biluochun tea output.This model shows that the first three most influential factors to tea yield among the 20 factors in the growing period are the daily average sunshine duration time in mid-February，the daily average highest temperature in the last ten days of February and the daily average minimum temperature in the first ten days of March.This model can be used for the production forecast of Biluochun tea.

Biluochun；climatic factors；stepwise regression；forecast model

O212；S11 MR（2000）Subject Classification：62J05

A

1672-0687（2016）02-0014-05

2015-03-18

国家自然科学基金重大项目（61190114/F0102）；国家自然科学基金资助项目（11171373）

王明月（1989-），女，河南信阳人，硕士研究生，研究方向：应用统计。

*通信联系人：徐常青（1966-），男，教授，博士，硕士生导师，E-mail：cqxurichard@mail.usts.edu.cn。