基于DOE方法的新型特种挂车车架优化设计

吴　波　胡三宝Wu Bo，Hu Sanbao（武汉理工大学　现代汽车零部件技术湖北省重点实验室，湖北　武汉　430070）

基于DOE方法的新型特种挂车车架优化设计

吴波胡三宝
Wu Bo，Hu Sanbao
（武汉理工大学现代汽车零部件技术湖北省重点实验室，湖北武汉430070）

以 DOE方法对国内某新型特种挂车车架进行轻量化设计，针对此挂车特殊的行驶工况，在 Hyperworks中对车架进行强度与模态分析。对特种连挂牵引工况应力不满足要求的现象利用试验设计分析车架各部分板厚对车架性能的影响，选择影响较大的板厚作为设计变量，通过哈默斯雷样本试验建立较高精度的响应面近似模型，以最小化质量为目标，各行驶工况许用应力为约束，基于自适应响应面优化算法对车架进行轻量化设计，最终减重0.27%，具有较好的轻量化效果。

挂车车架；有限元分析；试验设计；轻量化

0　引　言

随着经济全球化，各地商品的交流对运输效率提出了高要求。挂车运输方式多样，能够实现“甩挂运输”、“区间运输”等多种运输形式，具有装卸方便、安全可靠等特点被广泛使用[1]。新型特种挂车是一种特殊运输车辆，能够由单车牵引行驶也能够多车连挂行驶，可以提高运输效率，在未来具有广阔的应用前景。

试验设计（Design of Experiment，DOE）方法是解决复杂问题的科学手段，结合DOE方法能够建立精确的近似模型并用最少的试验次数获得最大信息，并依此进行轻量优化设计可以提高设计效率[2]。文中新型特种挂车具有多种复杂行驶工况，同时满足多工况车架的轻量化设计不仅在很大程度上能够降低整车质量，提高材料利用率，减轻轴荷，而且还能缩减车辆成本，减少汽车排放。

文中应用多学科有限元仿真软件包Hyperworks对某新型特种挂车车架进行有限元建模，对车架刚强度及模态进行分析。

通过试验设计确定车架优化设计对象并建立近似模型，最后基于自适应响应面算法提高车架强度，实现车架轻量化。

1　车架结构有限元分析

1.1车架有限元模型建立

新型特种挂车车架采用集装箱挂车形式如图1所示，单车额定载重30t。车架主要由贯穿前后的左右两侧箱型纵梁、边梁、侧翼梁以及纵梁之间不等距的若干根加强横梁组成。

此新型特种挂车车架与普通挂车相似，能够单车直接通过前端牵引销连接牵引车在公路行驶,也能够通过钩头实现多车连挂行驶。因此挂车车架分析主要包括有普通公路行驶工况以及特种连挂牵引工况。

由于车架各板件均为薄壁型结构，利用板壳单元（Pshell）划分网格，前后钩头采用四面体实体网格，各连接处采用Rigid单元模拟，悬架部分模拟为弹簧单元与刚性梁单元的组合，车架主要材料为车辆用高强度耐候钢Q450NQR1，其屈服强度为450MPa；最终模型如图2，整个模型共计87679个离散单元和85516个节点。

1.2车架静强度分析工况与结果

新型特种挂车根据其主要工作状态确定其车架静强度校核工况为普通公路行驶工况以及特种连挂牵引工况。在普通挂车公路行驶时主要分析公路行驶状态下弯曲、扭转（左侧第1轮悬空、第3轮悬空）、制动和转弯4种典型工况[3]。而特种牵引连挂行驶状态下主要分析牵引拉伸和牵引压缩工况。

在公路弯曲与扭转工况中垂向载荷系数取1.5，转弯与制动垂向载荷系数取1.2[4]，按实际安装位置加载，制动与转弯工况施加相应方向的惯性力等效。而特种牵引工况中根据设计要求，车架除受到垂向载荷外，还受到纵向1400kN压缩力（或1125kN拉伸力）以及40kN·m的扭转载荷。根据各工况不同要求设置相应约束，最终计算结果见表1。

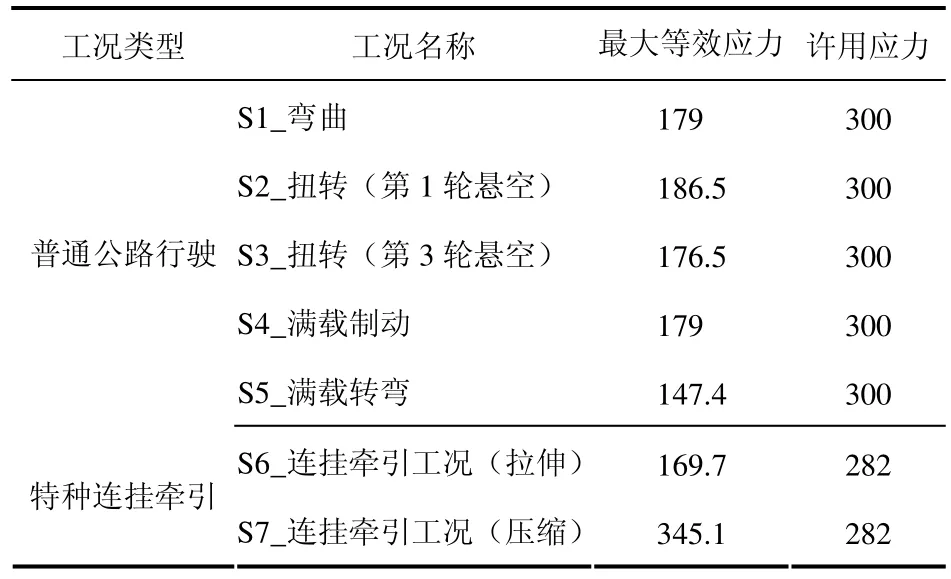
表1　挂车车架各工况强度计算结果MPa

由表1可以看出车架在普通公路行驶状态下各工况结构强度满足要求，且有较大优化空间。但在特种连挂牵引工况中由于两端受到较大的压缩力与垂向载荷共同作用，最大应力超过了许用应力，针对此现象进行后续轻量优化设计。

1.3车架模态分析

通过车架模态研究可以了解整体结构的动态特征，避免车架与外部激励产生共振。在车架自由状态下使用Block Lanczos算法对模态参数进行提取，忽略刚体模态，车架前5阶模态见表2。

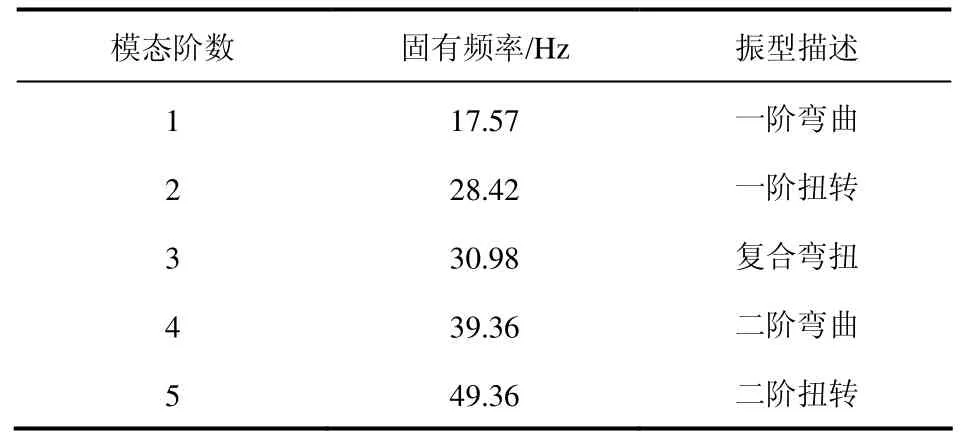
表2　车架前5阶非刚体模态

根据设计要求，在连挂特种牵引工况行驶时车架一阶固有频率应该大于10Hz[5]，满足设计要求。而一般公路行驶时非簧载质量的固有频率为6～15Hz，一阶频率高于此即满足公路要求，因此车架模态满足行驶要求。

2　车架板厚设计变量筛选

新型特种挂车车架主要由多种不同形状不同厚度的板件组成，需要对板厚进行尺寸优化。车架中影响车架结构性能的参数有很多，若将所有板件均考虑为设计变量，在进行DOE设计时会因为样本点数量过大导致计算时间相当长。因此，基于Hyperstudy筛选试验可以对选取的所有板件进行主效应分析，通过Hyperstudy中的主效应分析可以反映设计变量位于不同取值水平时对响应的影响程度从而反映灵敏度，最终得到设计变量的回归系数从而辨别出主要变量与次要变量，再对主要变量进行优化设计，避免优化的盲目性，提高设计效率。

对车架主要组成板件进行编号分类，整理初始设计变量见表3。

通过Plackett-Burman筛选试验得到各设计变量的回归系数如图3所示。由图3可以看出，Z1，Z2，Z4，Z6，Z9，Q1共6个变量对最终响应影响程度较高，选择这些变量作为优化设计变量，去除其余13个变量。

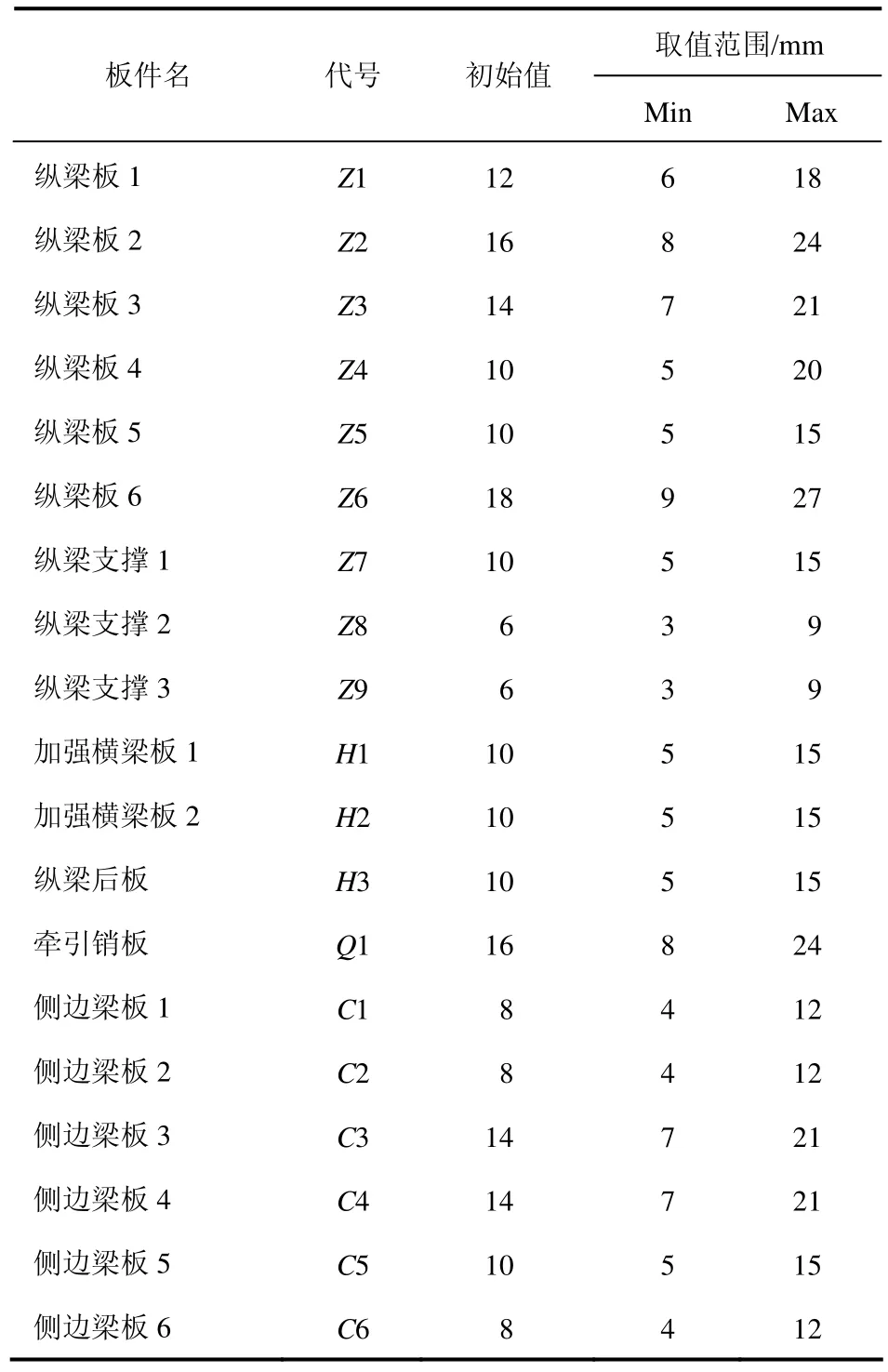
表3　初始设计变量参数

3　响应面近似模型的建立

在优化设计中，由于网格模型较为复杂，如果直接采用有限元模型进行求解会耗费大量的时间。建立近似模型即为通过对试验样本的考察从而建立响应与变量之间的函数关系，利用插值法对未考虑的变量响应进行估计，从而提高计算效率。近似模型的主要建立方法有响应面函数法（Response Surface Method，RSM）、径向基函数法（Radial Basis Function，RBF）及Kriging模型法等，其中响应面法是目前近似模型中应用最为广泛的一种方法[6]。

响应面法是一种通过包含变量与相应的独立样本点来确定近似模型的一种方法，主要用于变量与响应之间函数形式不确定的问题。具体函数形式如下[7]

筛选出设计变量后，通过哈默斯雷试验得到100个样本点作为创建响应面近似模型的输入矩阵，通过移动最小二乘法对响应面近似模型进行拟合，从而获得各响应的近似模型。由于移动最小二乘法构建的近似模型在DOE各采样点加权系数不为定值，而是从样本到取值点距离的函数，无法获得固定的近似函数解析式[8]。但近似模型建立完成后可采用复相关系数从R2来验证近似模型的精度，R2的值越接近1则代表近似模型与实际计算值越接近，其精度也就越高。R2的计算方法如下

其中，yi为第 i个样本点的响应，为第i个样本点的近似响应值，为所有样本点响应的均值。

近似模型各响应的R2值见表4。

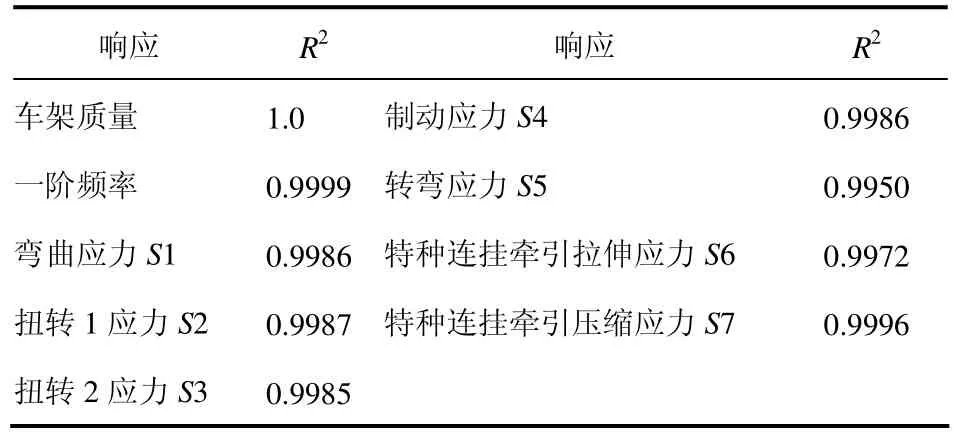
表4　响应的R2值

由表4可以看出车架近似模型的精度较高，各响应的R2值均在0.99以上，符合要求。

4　车架轻量优化

4.1基于自适应响应面算法的轻量化

自适应响应面法（Adaptive Response Surface Method，ARSM）是一种对迭代优化过程中产生的新的设计点加以利用从而获得更高的模型精度以及更快的逼近最优解的方法[9]。它结合了近似响应面模型和试验设计的方法，通过初始样本点拟合出近似模型后，针对目标函数的近似模型进行全局寻优，优化流程如图4所示。

针对新型特种挂车的多种行驶工况以及性能要求确定了优化目标以及约束。在普通公路所有行驶工况中车架最大应力不超过300MPa，针对特种连挂牵引行驶工况根据设计要求在拉伸与压缩时最大应力不超过282MPa，一阶频率不小于16Hz为优化应力约束，最后以车架质量最小化为目标，基于自适应响应面优化算法进行尺寸优化。优化设计中建立的数学模型如下

Minimizemass;

Stress1≤300MPa; Stress2≤300MPa;

Stress3≤300MPa; Stress4≤300MPa;

Stress5≤300MPa; Stress6≤282MPa;

Stress7≤282MPa;

Frequency≥16Hz；

整个优化共迭代30步收敛，质量迭代过程如图5所示。

优化后各板厚变化见表5。

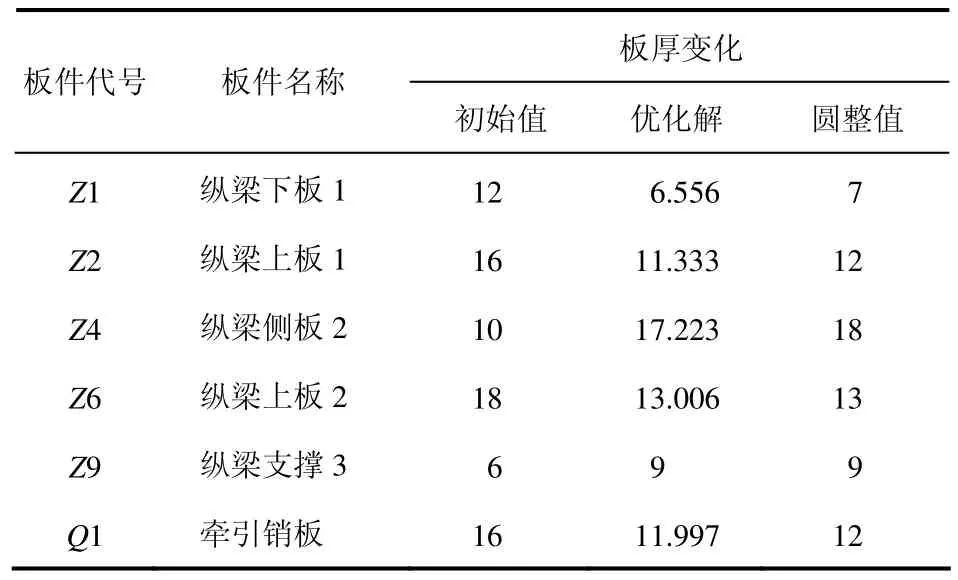
表5　优化前、后板厚变化mm

4.2优化方案验证与分析

近似模型与精确有限元模型之间因拟合精度等一系列问题存在误差，将最优解代入计算模型再次进行仿真，比较两者相对误差从而验证模型的准确性并讨论优化效果。分别将表中最优解代入有限元模型计算后与近似模型计算值进行比较，结果见表6。

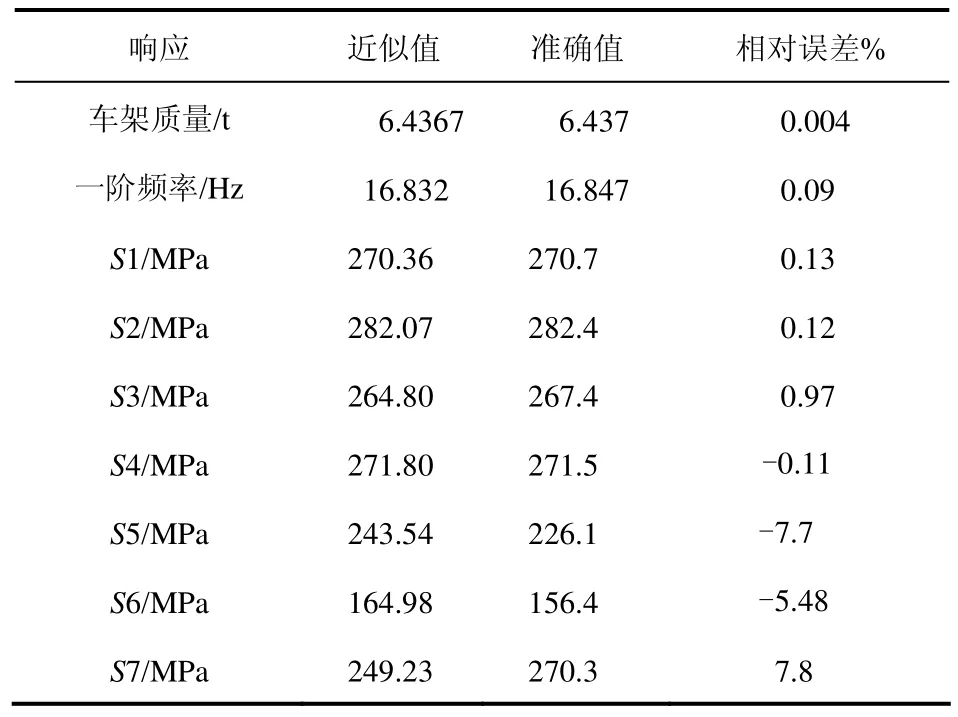
表6　近似模型与实际模型对比

由表6可以看出，响应面近似模型的准确度较高，特别是在质量、频率及普通公路行驶时弯曲、扭转、制动工况误差都在1%以内，具有极高的精度，而在公路转弯以及特种连挂牵引工况中误差相对较大，最大相对误差为7.8%。基于DOE方法建立的近似模型整体精度较高，优化结果可靠。

前文计算得到特种牵引工况受到压缩力时车架最大应力超过许用应力，优化后车架应力分布如图6所示。可以看出应力分布均匀，最大等效应力为270.3MPa，出现在悬架与车架后部连接处，小于许用应力282MPa，满足要求，优化结果较好。

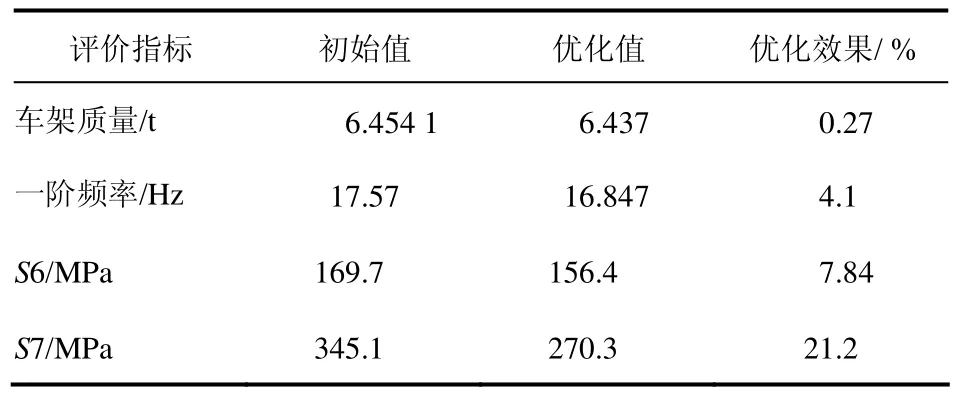
表7　车架优化效果分析

从表7可以看出，经过优化后，特种牵引工况应力均有明显减小，特别在特种牵引工况受到压缩力时最大应力下降了21.2%，优化后最大应力满足使用要求，同时模型总质量降低了0.27%。普通公路行驶各工况应力见表6，虽有所增大，仍然小于300MPa的许用应力要求，在质量降低的前提下频率有一定下降，为16.874 Hz，满足此特种挂车使用要求。

综上所述，经过优化后，车架材料利用率有所提高，在质量降低的同时保证了车架的普通公路行驶工况与特种连挂牵引工况下各应力与频率的使用要求，具有较好的轻量化效果。

5　结　论

DOE方法是一种理想的辅助优化手段，通过DOE方法能够有效地对新型特种挂车车架优化，通过Hyperstudy建立筛选试验，对设计变量进行筛选。采用哈默斯雷采样试验创建各响应具有较高精度的响应面近似模型。以车架各工况许用应力为约束，质量最小为目标，基于自适应响应面法对车架进行优化。在质量减少0.27%下特种牵引工况压缩应力减少了21.2%，获得了理想的优化结果，说明DOE方法能够大大提高优化设计效率，为复杂工况的新型特种车辆提供有效的优化手段。

[1]袁光涛，贾岩.轻量化设计：挂车发展新趋势[J].专用汽车，2006（4）：11-13.

[2]Mckay,M.D., Beckman, R.J., Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output From a Computercode [J].Technometrics,2000.

[3]王丰元，马浩，等.基于有限元法的半挂车车架分析[J].拖拉机与农用运输车，2009（8）：33-37.

[4]翟正锟，崔俊杰，郑伟茂，等.某鹅颈式半挂车车架有限元静态分析[J].中国农机化学报，2014（3）：175-178.

[5]王海滨.铁道工程轨道车车体结构仿真分析[D].大连：大连交通大学.2014.

[6]范子杰，桂良进，苏瑞意.汽车轻量化技术的研究与进展[J].汽车安全与节能学报，2014，5（1）：1-16.

[7]杨进，向东，姜立峰，等.基于响应面法的汽车车架耐撞性优化[J].机械强度，2010，32（5）：754-749.

[8]洪清泉，赵康，Optistruct & Hyperstudy理论基础与工程应用[M].北京:机械工业出版社，2013，345-347.

[9]兰凤崇，钟阳，庄良飘，等.基于自适应响应面法的车身前部吸能部件优化[J].汽车工程，2010，32（5）：404-408.

U463.83+1

A

10.14175/j.issn.1002-4581.2016.04.010

1002-4581（2016）04-0042-05

2016-02-26