基于平顺性的四轴重型商用车悬架参数优化

马骏昭Ma Junzhao（合肥工业大学　机械与汽车工程学院，安徽　合肥　230009）

基于平顺性的四轴重型商用车悬架参数优化

马骏昭
Ma Junzhao
（合肥工业大学机械与汽车工程学院，安徽合肥230009）

为提高车辆行驶平顺性，建立某四轴重型商用车悬架动力学模型，并对悬架参数进行优化。模型中，在车辆结构上考虑了平衡悬架和驾驶室，在悬架力学特性上考虑了阻尼非线性。采用遗传算法对车辆悬架的刚度特性和阻尼特性进行优化，优化综合考虑了车辆在不同路面等级下以不同车速行驶的平顺性。对优化前后驾驶室处垂直加速度均方值进行仿真对比，结果显示，优化后车辆行驶平顺性得到有效提高。

平顺性；四轴；平衡悬架；非线性；遗传算法

0　引　言1

随着消费者对车辆NVH（Noise，Vibration，Harshness，噪声、振动、声振粗糙度）性能要求的提高，作为评价车辆性能重要指标之一的汽车平顺性对于商用车变得愈发重要。良好的平顺性可以保证驾驶员的舒适性，使得驾驶员能够安全可靠地驾驶汽车，减少道路事故发生的可能性。对于车辆平顺性的研究，首先要建立可靠的模型，一个有效的模型不仅要依据车辆具体的结构和部件组成而建立，还要根据具体研究的问题进行适当简化，但是对于影响研究问题的关键因素不能简化省略。董明明建立了四轴车辆的半车6自由度模型，但是忽略了平衡悬架的特征[1]。付文奎建立了三轴车辆的半车 6自由度模型，模型考虑平衡悬架的特征，但是没有考虑到驾驶室[2]。李秀梅在Simulink中对三轴车辆的平顺性进行仿真，但是其半车 7自由度模型中没有考虑悬架阻尼的非线性特性[3]。

平衡悬架在多轴商用车中后桥上得到广泛的应用，它可以很好地保证平衡轴两侧的车轮同时与地面接触；多轴重型车辆的驾驶室对于驾驶员舒适性尤为重要，平顺性研究指标是驾驶室处的垂直加速度均方根值；因此，在建立模型时，保留了平衡轴和驾驶室这 2个特征，并且考虑了悬架阻尼非线性特征。在模型的基础上，对车辆在不同车速和不同路面下的行驶平顺性进行优化。该多轴重型商用车在悬架组成和整车布置方面都具有一定的代表性，为该类型车辆悬架参数的改进提供了可靠的依据，对其他商用车车型的平顺性研究具有指导和借鉴意义。

1　数学模型的建立

车型结构较为复杂，在建模时首先做出如下假设：

1）整车处于静平衡状态下的几何位移均为线性小位移；

2）路面不平度系数是不变的，只与相应的路面等级有关；

3）车辆在路面上匀速直线行驶；

4）不考虑整车质心在水平面内的任意方向的振动，只考虑垂直方向；

5）不考虑车身横向角的振动；

6）忽略车辆轮胎的阻尼力和空气的影响，把轮胎简化为等效刚体弹簧，并且忽略车轮的转向自由度，只考虑车轮的垂直运动。

基于以上假设，对该车辆建立半车 9自由度模型，如图1所示，模型的9个自由度分别为车身的垂向运动Z、车身的俯仰运动θ、第一轮的垂向运动 Z11、第二轮的垂向运动 Z12、第三轮的垂向运动 Z13、第四轮的垂向运动 Z14、平衡轴绕支点的转动θc、驾驶室的垂向位移Zs和驾驶室的俯仰运动θs。

该模型建立的动力学方程为

式中，a，b，c分别为一轴、二轴、平衡轴与车架铰接中心到整车质心的距离；d为三轴和四轴到平衡轴与车架铰接中心的距离；g，h为驾驶室前悬置、后悬置到驾驶室质心的距离；m为整车簧上质量；m1，m2，m3，m4为各轴簧下质量；mc为平衡轴质量；I，Ic，Is为车身、平衡轴、驾驶室绕车辆横向坐标轴的转动惯量；K11，K12，K13，K14为各轴轮胎径向刚度；y1，y2，y3，y4为各轴车轮受到的路面激励；F1，F2，F3，F4为各悬架作用力；Fc为车架对平衡轴的作用力；F5，F6为车架对驾驶室的作用力。

几何关系为

式中，Z21，Z22，Z23，Z24，Zc为各悬架和平衡轴的垂向位移。

对平衡轴单独进行受力分析，如图2所示。

得到方程

对平衡轴进行位移分析，位移关系为对驾驶室进行受力和位移分析，可以得到

车架对驾驶室的作用力为

式中，Zs1，Zs2为驾驶室两侧的垂向位移；Ks1，Ks2为驾驶室前悬置、后悬置垂向刚度；Cs1，Cs2为驾驶室前悬置、后悬置垂向阻尼。

由于驾驶室本身的转动相对于整车质心的转动很小，将转动位移关系作近似考虑，表达式为

式中，e，f为驾驶室前悬置、后悬置到整车质心的距离。

各悬架作用力为

式中，K21，K22，K23，K24为各轴悬架刚度；FC1，FC2，FC3，FC4为各悬架减振器阻尼力，对于减振器的阻尼特性，测得试验数据见表1。

根据试验数据采用幂函数拟合悬架阻尼非线性

式中，s1i，s2i，c1i，c2i为拟合系数，i=1，2，3，4。

2　基于Simulink的平顺性仿真

2.1随机路面激励

采用积分白噪声法模拟路面输入模型，将随机白噪声通过积分器和比例器得到时域上的随机路面输入。当频率指数w为2时，可以得到垂直速度功率谱密度公式

式中，n为空间频率，即为波长λ的倒数，为每米长度中所包含的波的个数，m-1；n0为参考空间频率，取0.1 m-1；Gq(n0)为参考空间频率n0下的路面功率谱密度值，即路面不平度系数，m3。

转化为时间频率下的路面不平度垂直速度功率谱密度

时间频率f与车速v的关系为

自功率谱密度与相关函数之间为傅里叶变换对的关系，可得空间频率功率谱密度

式中，ζ为路面上两点之间的距离，ζ与时域中自相关函数R(τ)的时间间隔τ之间的关系为

由此可以得出

根据以上各式可以得出时间频率的速度功率谱密度与空间频率功率谱密度的关系式为[4]

由此可知，路面轮廓在Matlab中可以由功率谱密度为k0的白噪声通过积分器实现，其中

路面输入表达式

式中，ω(t)为高斯白噪声，t为仿真时间。

车辆受到前后四轴的路面输入，在建立路面模型时，将二、三、四轴的路面输入作为一轴路面输入的时间延迟，在Simulink中采用Transport Delay模块来模拟路面激励的延时，并将白噪声功率谱密度幅值设置为0.04，建立模型如图3所示。

用该模型得到车速为30 km/h时4个车轮在B级路面的输入轮廓，如图4所示。

由已建立的路面模型的时域仿真结果，得到随机路面高程与B级路面的功率谱密度的对比曲线，如图 5所示。由积分白噪声方法产生的路面输入的功率谱密度接近理论值，路面输入模型满足要求。

2.2Simulink仿真模型的建立

将半车9自由度数学模型通过Simulink建立仿真模型如图6所示。

输入实际车辆满载状态下的参数，见表2。

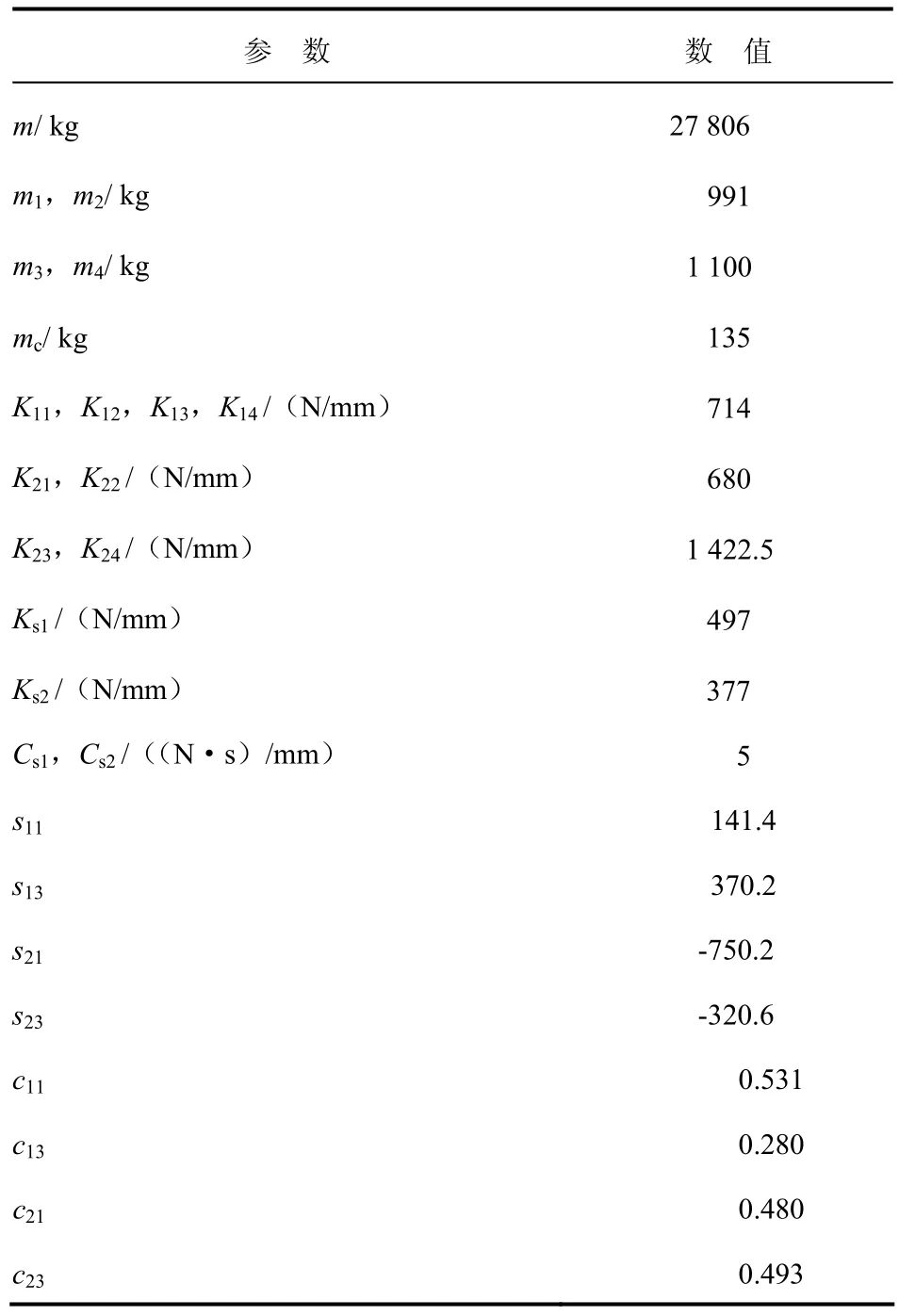
表2　模型输入参数表

2.3平顺性仿真

在随机路面的输入下，根据 ISO 02631-1：1997(E)标准《人体处于全身震动评估第一部分：一般要求》的规定[5]，当振动波形峰值系数小于9时，其中峰值系数是加权加速度时间历程 aw(t)的峰值与加权加速度均方根值aw之间的比值，用基本评价方法——加权加速度均方根值来评价振动对人体舒适度和健康的影响，文中建立了包括驾驶室在内的半车模型，故选用驾驶室处的垂直加权加速度均方根值作为平顺性的评价指标。

对Simulink仿真分析得到的驾驶室处的垂直加速度时间历程响应a(t)进行频谱分析，得到功率谱密度函数 Ga(f)，按式（19）计算得到驾驶室处的垂直加权加速度均方根值。

频率加权函数

在Simulink中对车辆在B级路面和C级路面下，以车速40，50，60，70，80 km/h行驶进行平顺性仿真，结果见表3。

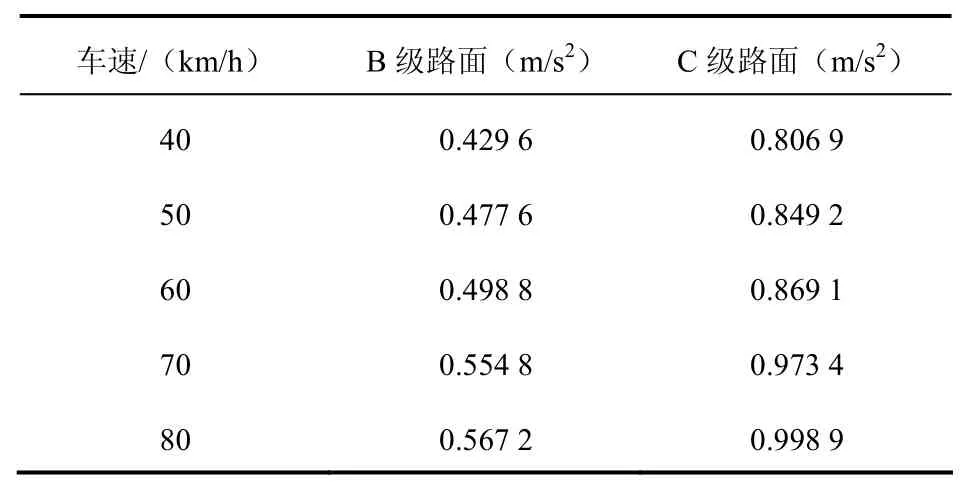
表3　驾驶室处的垂直加权加速度均方根值

3　悬架参数的优化

对于悬架的优化，优化对象可以从悬架几何特性参数入手，即悬架三维模型中各关键点的坐标或各部件的几何尺寸[6]，还可以从悬架系统力学特性参数入手，例如弹簧的刚度特性，减振器的阻尼特性以及限位块特性等[7]。采用遗传算法对悬架的刚度特性和阻尼非线性特性进行优化。遗传算法以达尔文的生物进化论和遗传学为基础，通过模拟自然的进化过程来求解最优解，在优化的过程中，遗传算法可以自动地去获取其范围内的有效信息，并以此寻求优化的途径；其应用范围较广，可以解决很多学科中的问题，并且对优化对象本身不具有依赖性，容错率较好，不容易陷入局部最优[8]。

1）确定目标函数

本车型作为商用车，考虑其在不同车速和不同路面下的平顺性。对于车速，考虑40，50，60，70，80 km/h这5种车速下的情况，对于路面不平度，考虑B级路面和C级路面这2种路面下的情况。优化综合考虑不同路面下不同车速行驶的平顺性，对每种情况取相应的加权系数，设定目标函数

式中，aB1(x)，aB2(x)，aB3(x)，aB4(x)，aB5(x)分别为B级路面下40，50，60，70，80 km/h车速下的驾驶室处的加权加速度均方根值。aC1(x)，aC2(x)，aC3(x)，aC4(x)，aC5(x)分别为 C级路面下40，50，60，70，80 km/h车速下的驾驶室处的加权加速度均方根值。

2）选择设计变量

对悬架的刚度和阻尼特性进行优化，选取设计变量

优化的设计变量的范围设定为原始值的0.8～1.2倍之间。

3）约束条件

根据汽车理论，为保证车辆行驶平顺性，需要对车辆的悬架动挠度和车轮相对动载荷进行约束[9]。

对悬架动挠度进行约束，即各轴悬架动挠度均方根值应满足式（23），这样可以保证各轴悬架撞击限位块的概率小于0.3%。

式中，fd为悬架动挠度；dfσ为悬架动挠度均方根值；[fd]为悬架动挠度许用值，取80mm。

对车轮相对动载荷进行约束，各轴车轮相对动载荷均方根值应满足式（24），这样可以保证各轴车轮与地面脱离的概率小于0.15%。

式中，Fd为车轮与路面的动载；G为车轮作用于路面的静载，Fd/G为车轮与路面的相对动载；为车轮相对动载均方根值。这样可以保证各轴车轮与地面脱离的概率小于0.15%。

各设计变量的优化结果见表4。

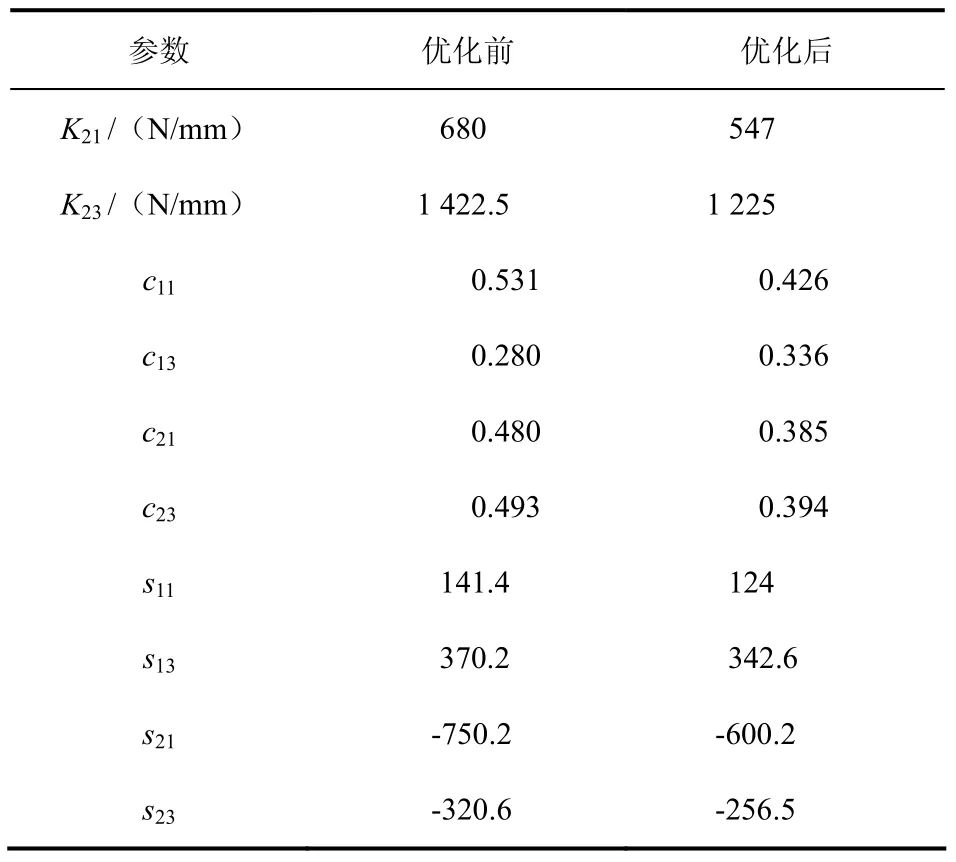
表4　悬架参数优化前后对比

对于目标函数的优化结果见表5。

表5　优化结果对比

选取在B级路面下车速为60 km/h车辆驾驶室处的垂直加权加速度时间响应和功率谱密度优化前后进行对比，如图7、图8所示。

4　结束语

对某带平衡悬架的四轴重型商用车建立半车9自由度数学模型，模型保留车辆的驾驶室和平衡悬架的结构特征，并且考虑悬架的阻尼非线性特征，并以驾驶室处的加权加速度均方根值作为平顺性评价指标，在Simulink中对模型进行平顺性仿真分析。综合考虑车辆在不同路面下不同车速行驶的平顺性，采用遗传算法对悬架的刚度特性和阻尼非线性特性进行优化，通过改进悬架参数使车辆行驶平顺性更好。

[1]董明明，杨猛.多轴越野车辆轴间刚度和阻尼的最优匹配[J].车辆与动力技术，2014(4):40-44.

[2] Fu W, Ling F, Peng M, et al.Comparison of Wheelbase Filtering Effect and Suspension Tuning Between Two-axle and Tri-axle Vehicle with Tandem Suspension[C]//Proceedings of the 2012 International Conference on Computer Application and System Modeling.Atlantis Press, 2012.

[3]李秀梅.三轴重型车辆行驶平顺性研究[D].长春：吉林大学，2011.

[4]周长城.车辆悬架设计及理论[M].北京：北京大学出版社，2011.

[5]Kubota A, Kato H, Yamaguchi H, et al.Unsteady Structure Measurement of Cloud Cavitation on a Foil Section Using Conditional Sampling Technique[J].Journal of Fluids Engineering,1989,111(2):204-210.

[6]丁亚康，翟润国，井绪文.基于 ADAMS/Insight的汽车悬架定位参数优化设计[J].汽车技术，2011（5）：33-36.

[7]吕彭民,和丽梅,尤晋闽.基于舒适性和轮胎动载的车辆悬架参数优化[J].中国公路学报，2007，20（1）：112-117.

[8]周明.遗传算法原理及应用[M].北京：国防工业出版社，1999.

[9]余志生.汽车理论[M].北京：机械工业出版社，2009.

U462.3

A

10.14175/j.issn.1002-4581.2016.04.003

1002-4581（2016）04-0009-07

国家新能源汽车创新工程（财建2012[1095]）。

2016-03-15